交直流混合配电系统的供需双侧互动优化调度

吴永昌，李凤婷*，赵 星，李 鹏

(1.新疆大学 电气工程学院，新疆 乌鲁木齐 830047；2.国网新疆电力有限公司 乌鲁木齐供电公司，新疆 乌鲁木齐 830011)

直流配电网通过变频装置控制交流网络谐波及进行无功补偿，能提高分布式可再生能源接入的可控性与可靠性.配电网调度应采用更科学的调度策略，以解决源荷预测性差、可调度资源不足等问题.在调度过程中，除考虑众多分布式可控资源外，还涉及集中式可再生能源.交直流混合配电系统(hybrid AC/DC distribution systems,简称HAC/DCDS)出现后，可调度资源、市场主体、接入负荷的增加，使配电网调度面临挑战.

目前，基于HAC/DCDS的智能优化调度研究相对较少，大部分集中于交直流微电网优化，如极端情况下微网运行方式的优化、利用鲁棒理论使配电网的利润最大等.多种能源参与下的供给与消费协同、集中与分布式可再生能源发电功率的不确定性，是HAC/DCDS面临的主要问题.文献[6]利用HAC/DCDS灵活性及可控性，提出分布式控制结构以缓解发电不确定性对系统调度的影响.需求响应是平抑电功率波动的有效手段.对可控资源统一管理、集中调度，能够有效管理分布式可再生能源及可控负荷，分摊市场风险，提高盈利能力.

对模型的优化求解是难点之一.列和约束算法、分段线性化等传统方法虽能兼顾求解效率及速度，但这些方法要求目标函数必须是严格定义的，且对初值的依赖较大.因此，越来越多的研究人员将求解大规模、混合整数、非凸、非线性问题的优化算法用于电力系统优化调度.

笔者提出基于Stackelberg博弈的HAC/DCDS供需双侧互动优化调度模型.该优化调度模型利用大系统分解协调理论，将上级电网、HAC/DCDS和需求侧看成不同的市场主体.优化调度过程中的信息互相传递，使各市场主体同时完成供需双侧的博弈互动.针对多目标、非凸、非线性规划问题，提出一种改进鲸鱼算法(improvement whale optimization algorithm，简称IWOA)，该算法可解决模型中的复杂约束问题.选取修改的IEEE-33交直流混合配电系统作为算例进行仿真分析.

1 HAC/DCDS优化调度模型

1.1 HAC/DCDS的供需双侧互动

图1为HAC/DCDS的供需双侧示意图.参与供需双侧互动的市场主体包括：HAC/DCDS、上级电网和用户.用户侧按照用电特性分为如下3类：①常规负荷(conventional load，简称CL)，如生活日常用电负荷；②可切负荷(resectable load，简称RL)，如商业可切负荷、生产可切负荷等；③可转移负荷(transferable load，简称TL)，如空调、热水器等.

图1 HAC/DCDS的供需双侧示意图

HAC/DCDS的供需双侧互动使用Stackelberg博弈.与供给侧的博弈互动时，HAC/DCDS是作为上级电网(leader)的follow；与需求侧的博弈互动时，HAC/DCDS是作为需求侧 (follow)的leader.上级电网考虑自身收益、环境污染，调整对HAC/DCDS的电能出售量；HAC/DCDS考虑所辖分布式新能源不确定性带来的备用成本及弃风弃光成本，优化接入的可再生能源的电功率.优化过程中，信息的传递使各市场主体完成供需双侧的博弈互动.

1.2 数学模型

1.2.1 上级电网

上级电网通过调节管辖范围内火电机组进行能源调度，满足HAC/DCDS对电能的需求.以上级电网经济效益最大和污染排放量最小为目标函数.模拟上级电网与HAC/DCDS的互动时，只考虑出售给HAC/DCDS的电能收入、火电机组的发电成本及污染.

(1)目标函数

发电成本最小，即

(1)

有害气体排放量最小，即

(2)

其中：

α

，

β

，

γ

，

ξ

为第

i

台火电机组的排污系数.

(2)约束条件

发电总量约束为

(3)

火电机组运行约束为

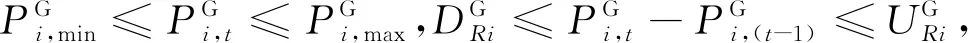
(4)

1.2.2 HAC/DCDS

(1)目标函数

HAC/DCDS的运营利润最高，即

(5)

其中

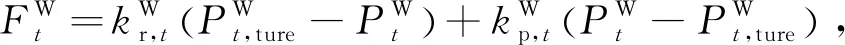
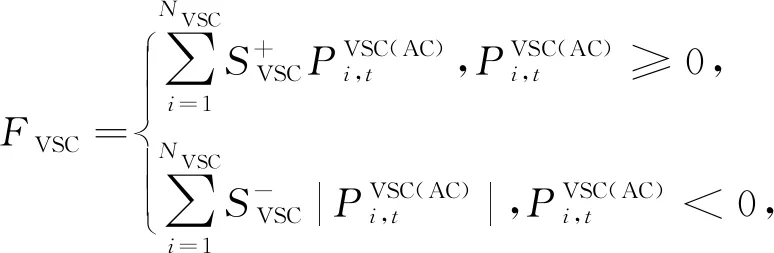
HAC/DCDS的功率与用户层的调度功率偏差最小，即

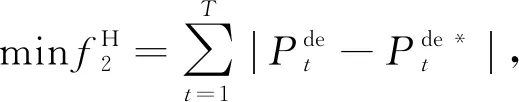
(6)

(2)约束条件

电量平衡约束为

(7)

风电、光伏输出功率约束为

(8)

另外，还有交直流配电系统节点的功率平衡约束、电压稳定约束.

1.2.3 用 户

(1)目标函数

调度计划偏差最小，即

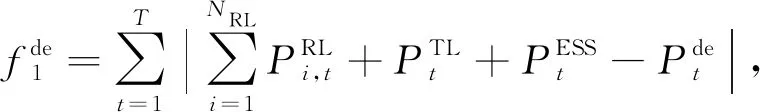
(9)

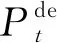
经济、社会效益最优，即

(10)

其中

(2)约束条件

可切负荷运行约束为

(11)

可转移负荷运行约束为

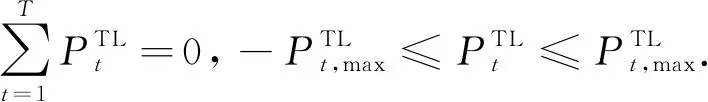
(12)

储能系统运行约束为

SOC

E

≤

E

≤SOC

E

，

(13)

(14)

E

=(1-

ρ

)

E

-1-

ΔE

，

(15)

(16)

其中：SOC表示储能系统的荷电状态；

E

为储能系统的额定容量；

E

为储能系统

t

时刻的容量；

η

，

η

分别为储能系统的充、放电率；

ρ

为储能系统的放电功率.

2 优化调度模型的求解

2.1 问题描述

2.2 改进的鲸鱼算法

标准鲸鱼算法(whale optimization algorithm，简称WOA)具有原理简单、参数少、寻优强等特点，求解精度和收敛速度均优于粒子群算法与遗传算法，已成功应用于大规模优化问题上.但标准WOA不能有效平衡全局搜索与局部搜索，鉴于此，笔者提出IWOA.设定一个探索固定值

A

_constant,当

A

≥

A

_constant时执行全局搜索，反之执行局部搜索.IWOA迭代的方式为

(17)

(18)

2.3 约束条件处理

(1)对多层模型中的运行界限约束，如式(4)，(9)，(12)，可直接利用元启发式算法处理.对于火电机组的爬坡约束，可通过动态更新机组出力范围，转化为如下边界约束

(19)

(2)对于电量平衡、可转移冷热负荷及储能系统的可持续运行约束，用动态松弛进行处理.

2.4 求解流程

图2为求解流程图，包括决策变量的寻优、约束处理、最优折中解的提取等.各市场主体互相独立，对不同种群分别进行优化，优化过程中种群间信息互相传递，使各市场主体效益均达最优.

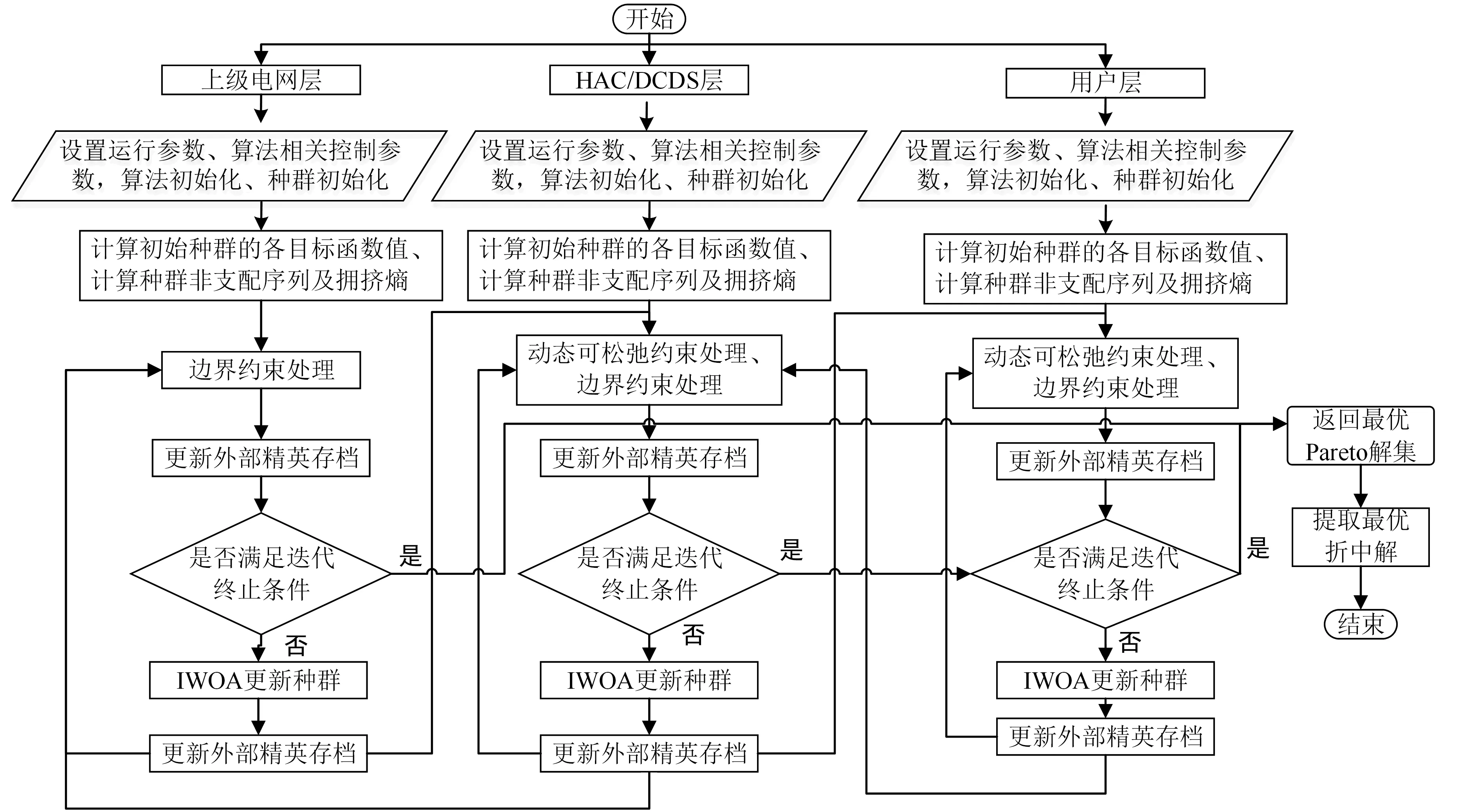
图2 求解流程图

3 仿真分析

选取修改的IEEE-33交直流混合配电系统作为算例.图3为修改的IEEE-33交直流混合配电系统，其中橘色为交流线路，蓝色为直流线路；两个VSC规格相同，其电抗为1.5 Ω，电阻为0.3 Ω，额定容量为2 MVA，无功补偿区间为300～300 kvar.配电系统额定电压、各支路阻抗见文献[18].

图3 修改的IEEE-33交直流混合配电系统

需求管理中心管辖的可控资源及其参数见表1.风电、光伏及VSC的成本系数见表2.

表1 需求管理中心管辖的可控资源及其参数

表2 风电、光伏及VSC的成本系数 元·(kW)-1

风电、光伏及负荷功率预测结果见图4.为分析HAC/DCDS与需求侧间的博弈互动，设置情景1～5.情景1:HAC/DCDS与需求侧间无互动；情景2:仅可切除负荷(RL1,RL2)参与互动；情景3:仅可转移负荷(TL)参与互动；情景4:仅可控负荷(包括可切除负荷及可转移负荷)参与互动；情景5:所有可控资源均参与互动.

图4 负荷及风电光伏功率预测结果

表3为情景1～5的调度结果.由表3可知，需求管理及HAC/DCDS中可调度资源的越多，调度就越灵活、调度的偏差就越小、社会效益提升的负荷就越多、用电舒适度就越高.

表3 情景1～5的调度结果

进一步分析需求管理对其他调度结果的影响.图5为不同情景下联络线的输送功率及VSC的转换功率.由图5可知：随着需求管理可用资源增加，HAC/DCDS的灵活性大幅提高；参与互动的可控资源数量越多，VSC转换功率的波动性越小，VSC的调度成本越小；所有可控资源参与互动时，联络线可向上级电网传输更多的电量，HAC/DCDS的经济利益更高.

图5 不同情景下联络线的输送功率及VSC的转换功率

图6为所有需求管理、火电机组及联络线计划功率.由图6可知：耗电低谷时，需求管理中心向HAC/DCDS供电，以提高自身经济利益；用电高峰时，HAC/DCDS向需求管理中心供电以维持供需平衡.考虑分时电价的影响，电价较高时段HAC/DCDS通过联络线向上级电网输送大量电能，以增加利润；电价较低时段HAC/DCDS只输送少量电量，剩余部分用来满足可转移负荷及储能系统的需求.

图6 所有需求管理、火电机组及联络线计划功率

4 结束语

笔者提出HAC/DCDS供需双侧互动优化调度模型，该模型基于Stackelberg博弈理论与多层调度模式，考虑HAC/DCDS的供需双侧互动.经算例仿真得出如下结论：

(1)供需双侧博弈互动，能均衡各层主体的收益，实现电力系统的可持续发展.

(2)HAD/DCDS能提高可再生能源并网的灵活性，在保证自身负荷需求的前提下将剩余电量平稳输送至上级电网.

(3)需求管理能应对发电功率的波动，但盲目增加可调度资源使决策变量可行域变窄、多层计划偏差增大、调度效果变差.

(4)IWOA能求解具有复杂约束条件的非凸、非线性规划模型.