分数阶线性系统初值学习的PDα型迭代学习控制
窦建君,张克军,刘万利,孙天凯
(1.徐州工程学院 数学与统计学院,江苏 徐州 221018;2.徐州工程学院 信息工程学院,江苏 徐州 221018)
迭代学习控制是结合人工智能与自动控制理论形成的一类自适应控制技术,被广泛应用于各种工程控制领域.随着分数阶微积分理论和其他智能优化算法的发展,对于复杂度不断提高的控制系统,为了实现对其输出轨迹的精确跟踪,Chen等首次提出了D型分数阶迭代学习控制算法,将迭代学习控制的应用范围从整数阶系统推广到分数阶系统.经过几十年的发展,国内外研究者对不同类型的分数阶系统迭代学习控制算法的收敛性、鲁棒性等学习性态进行了深入分析,并取得了一系列的成果.
在现有的研究分数阶系统迭代学习控制的文献中,大部分是假设所研究的系统在每一次的迭代过程中初值与期望初值相同,否则,无论多小的初态偏差都会导致系统的实际输出不能精确跟踪期望输出.但是,在实际工程中,保持每一次迭代的初值与期望初值相同是非常困难的.目前,一些学者对分数阶系统的初值问题进行了研究,但研究成果还不多.例如,对于初值固定的分数阶线性系统,文献[13]提出了带初值误差的开闭环P型迭代学习控制算法,并研究了算法的收敛条件.针对具有任意初值的整数阶线性时变系统,文献[14]提出了初值学习的D型分数阶迭代学习控制算法,消除了初始偏差对系统的影响.而对于具有任意初值的分数阶非线系统,文献[15]研究了初值学习的开环和闭环P型迭代学习控制算法的收敛性.文献[16]将这一结论推广到分数阶非线性时滞系统.文献[17]讨论了分数阶线性时不变系统带初值修正的PD型迭代学习控制算法的收敛性,但该算法需要假设系统初值偏差是有界的,不能满足任意初值的情况.对于拥有任意初值的分数阶线性时不变系统,论文提出一种基于初值学习的PD型分数阶迭代学习控制算法,并在λ
-范数的意义下讨论了控制算法收敛的充分条件,严格的理论分析和仿真验证了该算法的合理性和有效性.1 预备知识

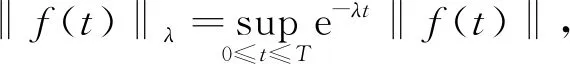
λ
>0,‖f
(t
)‖为某种向量范数.定义2
函数f
(t
)在[t
,t
]上的α
阶分数阶积分的定义为
f
(t
)在[t
,t
]上的Caputo左侧和右侧分数阶微分的定义分别为


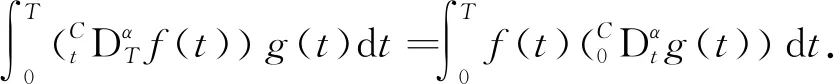
定义3
双参数的Mittag-Leffler函数定义为
其在分数阶微积分中的作用非常重要.
特别地,当β
=1时,单参数Mittag-Leffler函数定义为




引理3
初值问题
的解为



z
+1|≤θ
|z
|+|δ
|,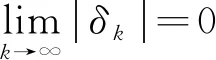
2 系统描述
考虑一类分数阶线性时不变系统
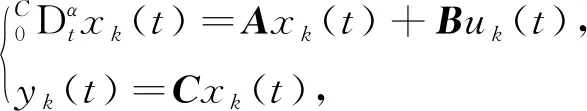
(1)

为了证明方便,假设分数阶系统(1)满足以下条件.
假设1
分数阶线性时不变系统(1)的期望输出y
(t
)在[0,T
]上α
阶微分存在,对于给定的y
(t
),有唯一期望控制输入u
(t
)和理想状态x
(t
),使得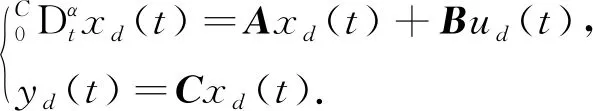
(2)
假设2
为行满秩矩阵.设u
(t
)(t
∈[0,T
])为一任意值,为首次控制输入.每次迭代学习时,假设分数阶线性系统(1)的初值x
(0)都不相同,为了使其输出能够精确跟踪期望输出,针对系统的控制输入和系统初值,设计如下初值学习的开闭环PD型分数阶迭代学习算法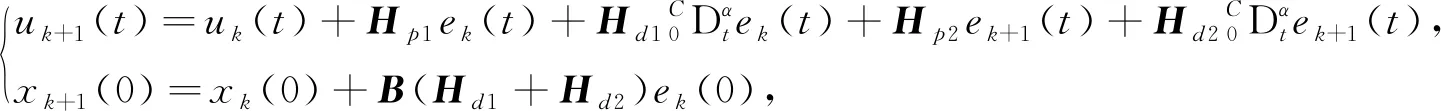
(3)
其中:e
(t
)=y
(t
)-y
(t
)为第k
次迭代学习时的跟踪误差;1,1为学习增益矩阵,2,2为反馈增益矩阵.3 收敛性分析
定理1
当初值学习的开闭环PD型控制算法(3)作用于分数阶线性时不变系统(1)时,若满足条件:(I)ρ
=‖-1-2‖<1;(II)ρ
ρ
<1.
其中:ρ
=‖(+2)‖,ρ
=‖-1‖,则当k
→∞时,系统输出y
(t
)在[0,T
]上一致收敛于期望输出y
(t
),即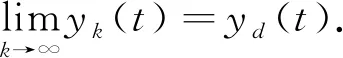
证明
根据引理2,由系统(1),有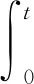
(4)
由(3)式,可得
e
+1(t
)=y
(t
)-y
+1(t
)=e
(t
)-(x
+1(t
)-x
(t
))=


(5)
由引理1,2,有





(6)
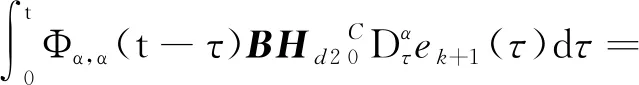

(7)
将(6),(7)式代入(5)式,有

e
+1(τ
))dτ
-1e
(t
)+CΦ
,1(t
)1e
(0)-



(8)
将t
=0代入(8)式,有e
+1(0)=(-1)e
(0)-2e
+1(0)+Φ
,1(0)2(e
+1(0)-e
(0))=(-1-2)e
(0).
(9)
(9)式两边同时取范数,有
‖e
+1(0)‖≤‖-1-2‖‖e
(0)‖=ρ
‖e
(0)‖.
(10)
根据条件(I),有

(11)
(8)式可变为


(12)
由假设2可知,存在反馈增益矩阵2,使得矩阵+2可逆.因此,(12)式两边左乘(+2),可得e
+1(t
)=

Φ
,1(t
)2(e
+1(0)-e
(0)).
(13)
由引理2可知,当t
∈[0,T
]时,有
故
‖Φ
,1(t
)‖≤c
M
,‖Φ
,(t
)‖≤c
M.
(13)式两边同时取范数,整理可得
‖e
+1(t
)‖≤‖(+2)‖‖-1‖‖e
(t
)‖+
(14)
其中
β
=c
M
‖(+2)‖‖‖‖1+1‖,β
=c
M
‖(+2)‖‖‖‖2+2‖,β
=c
M
‖(+2)‖‖‖‖2‖.
(14)式两端同乘以e-,并计算上确界,整理得
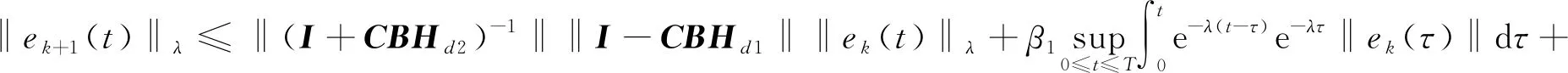



(15)
故
‖e
+1(t
)‖≤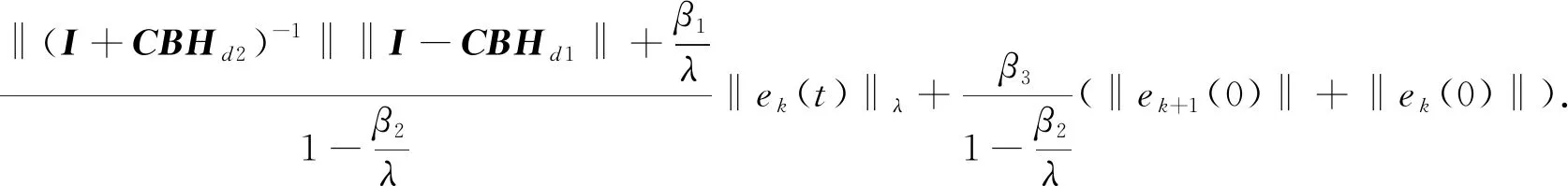
(16)
根据定理1条件可知,存在一充分大的λ
,使得
(17)
故
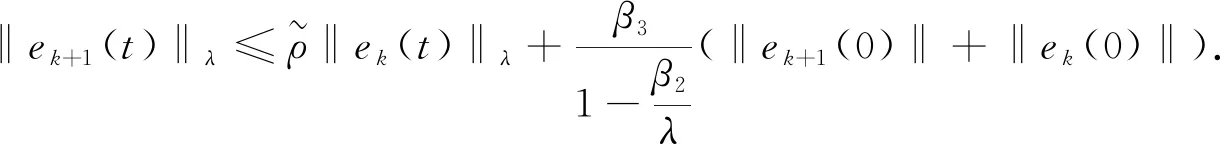
(18)
根据(11),(17),(18)式及引理4,有

故

定理1证毕.
当2=2=0
时,控制算法(3)退化为初值学习的开环PD型控制算法
(19)
定理2
当初值学习的开环PD型控制算法(19)作用于分数阶线性时不变系统(1)时,若满足条件ρ
=‖-1‖<1,则当k
→∞时,系统输出y
(t
)在[0,T
]上一致收敛于期望输出y
(t
),即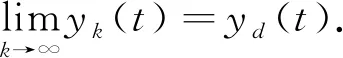
0
时,控制算法(3)退化为初值学习的闭环PD型控制算法
(20)
定理3
当初值学习的闭环PD型控制算法(20)作用于分数阶线性时不变系统(1)时,若满足条件:(I)ρ
=‖(+2)‖<1;(II)ρ
=‖-2‖<1.
则当k
→∞时,系统输出y
(t
)在[0,T
]上一致收敛于期望输出y
(t
),即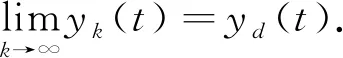
定理2,3的证明与定理1类似,故不再赘述.

注2
对于分数阶线性时不变系统,论文只分析了初值学习的一阶PD型控制算法收敛的充分条件,类似地,可以继续讨论初值学习的高阶PD型算法的收敛性问题.3 数值仿真
考虑如下分数阶线性时不变系统

(21)
其中:系统的运行区间为[0,1].
给定期望输出如下
y
(t
)=12t
(1-t
),t
∈[0,1].
为了验证控制算法对初值的敏感性,首次迭代时的初值x
(0)随机取值,但不等于期望初值x
(0).
首次迭代时,采用rand函数随机生成初始控制输入u
(t
)的值.在初值学习的开闭环PD型控制算法(3)中,1,1,2,2的参数分别为0.
8,1.
9,0.
6,2.
2,α
=0.
8,可以算出ρ
=0.
18<1,ρ
=0.
62<1,ρ
ρ
=0.
43<1,满足定理1,2的收敛条件.当传统的开闭环PD型控制算法被应用于分数阶线性时不变系统(21)时,给定的期望输出y
(t
)以及第4,8次迭代学习时的实际输出如图1所示,系统的跟踪误差曲线变化趋势如图2所示.从图1,2中可以看出,当系统初值随机取值时,在传统的开闭环PD型控制算法作用下,系统输出与期望输出之间存在偏差;随着迭代次数的递增,无法实现系统的实际输出对给定期望输出的精确跟踪,只能跟踪到期望输出的某邻域内,此时,系统的跟踪误差都是收敛有界的.
图1 开闭环PDα型控制算法在第4,8次迭代的输出

图2 开闭环PDα型控制算法的跟踪误差变化趋势
在同一仿真环境下,对初值学习的开闭环PD型控制算法(3)的收敛性进行仿真实验.当算法(3)被应用于分数阶系统(21)时,给定的期望输出y
(t
)以及第4,8次迭代学习下的实际输出如图3所示,系统的跟踪误差曲线变化趋势如图4所示.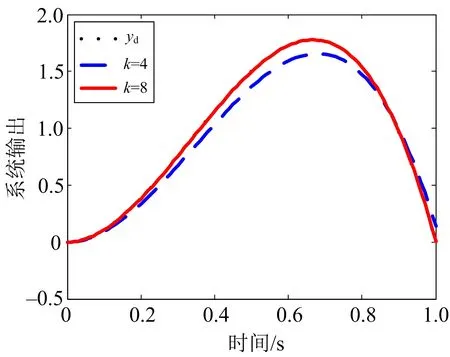
图3 初值学习的开闭环PDα型控制算法在第4,8次迭代的输出

图4 初值学习的开闭环PDα型控制算法的跟踪误差变化趋势
由图3,4可知,当系统初值随机取值时,在初值学习的开闭环PD型控制算法(3)作用下,随着迭代次数的递增,在整个区间[0,1]上,系统输出能够精确跟踪给定的期望输出,即系统的跟踪误差是趋于零的.
上述两种算法的仿真是在相同环境下进行的,由仿真结果可知,较之传统的开闭环PD型控制算法,论文的基于初值学习的开闭环PD型控制算法改进效果十分明显,消除了随机初值对系统的不良影响.在上述条件下,初值学习的开环PD型控制算法(19)、初值学习的开闭环PD型控制算法(3)分别被应用于分数阶线性系统(21)时,系统的跟踪误差变化曲线如图5所示.
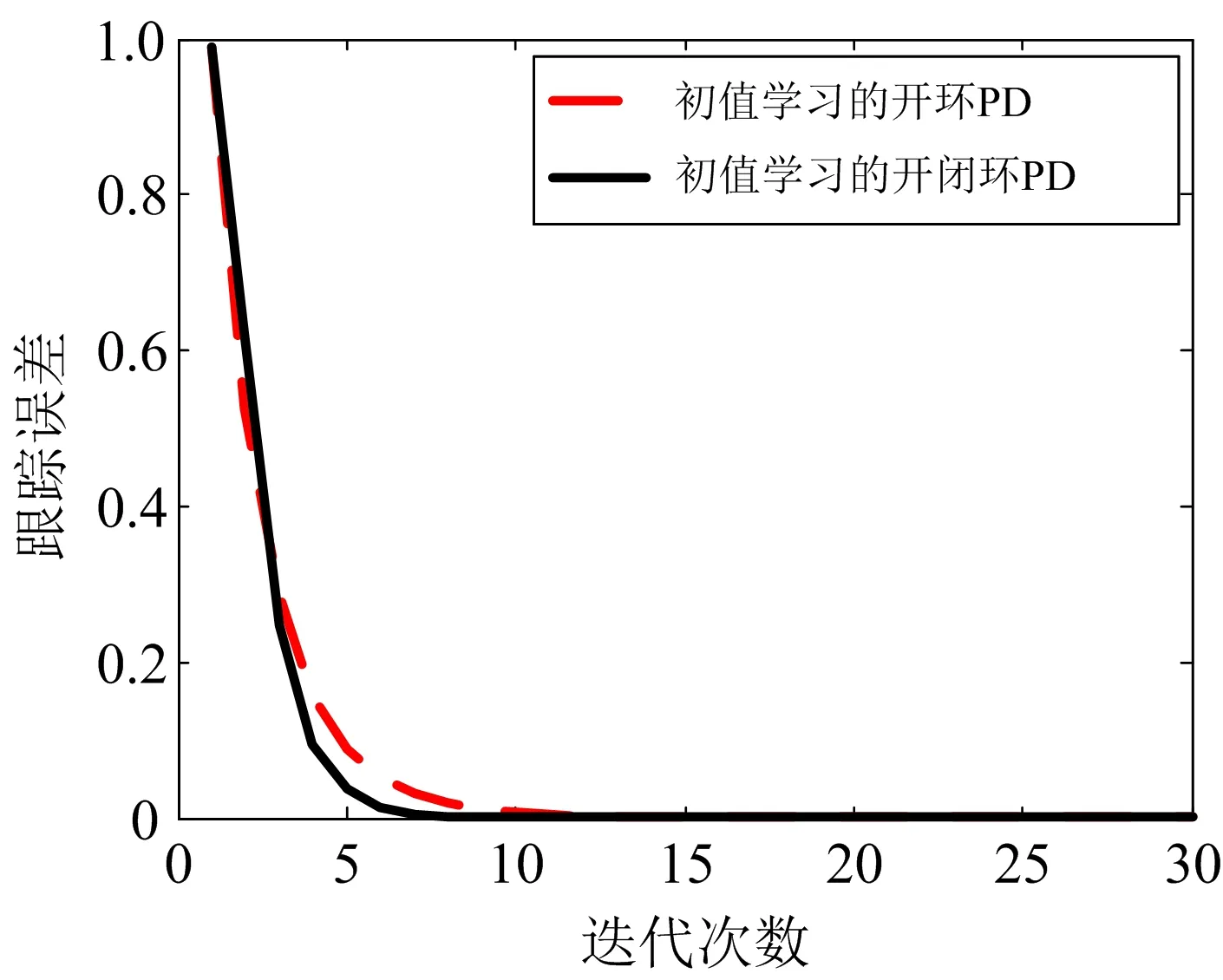
图5 初值学习的开环、开闭环PDα型控制算法的跟踪误差比较
由图5可知,随着迭代次数递增,在控制算法(3)、(19)的分别作用下,系统的跟踪误差都是趋向于零的.当ρ
ρ
<ρ
<1时,控制算法(3)迭代8次便可达到误差范围(0.002 5),而初值学习的开环PD型控制算法(19)需要12次迭代才能达到上述效果.可见,如果选取适当的学习增益,初值学习的开闭环PD型控制算法(3)比初值学习的开环PD型控制算法(19)具有更快的收敛速度,这一结果与注1的结论是相符的.4 结束语
为了解决由于系统的初值与期望初值不一致引起的系统输出不能精确跟踪期望输出的问题,针对具有任意初值的分数阶线性时不变系统,提出了基于初值学习的开闭环PD型分数阶迭代学习控制算法,在λ-范数的意义下,经过严格的数学证明,给出了控制算法收敛的充分条件.理论分析和仿真实验结果表明,当系统初值随机取值时,在论文算法的作用下,经过迭代学习后,系统输出能够完全跟踪期望输出.

