带时滞项的高阶Kirchhoff型方程的惯性流形

王利波,徐瑰瑰,林国广

(1.凯里学院 理学院,贵州 凯里 556011；2.云南大学 数学与统计学院，云南 昆明 650091)

无穷维动力系统的长时间性态已经得到广泛研究.在非线性偏微分方程无穷维动力系统的长时间行为的研究中，惯性流形的概念起着重要作用.惯性流形是系统的有限维的正不变的Lipschitz流形，在有限维的惯性流形上，可以把无穷维动力系统转化为有限维动力系统,有利于对无穷维动力系统的研究.文献[11]首次考虑半线性抛物方程情形下的非线性偏微分方程的惯性流形,文献[12]考虑二阶时滞波方程的惯性流形,文献[13]考虑带有时滞项的高阶Kirchhoff型方程的拉回吸引子的存在性.

论文讨论如下带时滞项的高阶Kirchhoff型方程解的适定性及其惯性流形的存在性

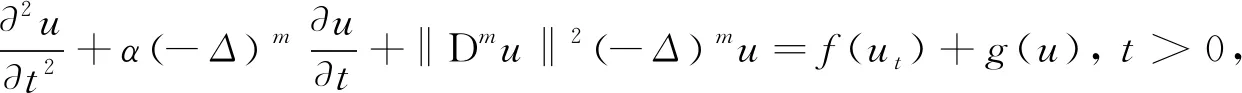
(1)

边界条件为

(2)

初始条件为

(3)

1 基本假设

Ae

=

μ

e

，

‖

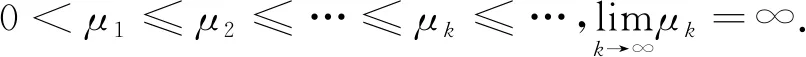
v

‖=sup{‖

A

v

(

θ

)‖:

θ

∈[-

r

,0]}

.

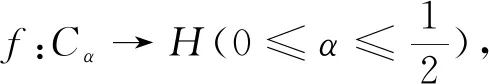
(F2)

f

(0)=0.

|

f

(

ξ

)-

f

(

η

)|≤

L

‖

ξ

-

η

‖

.

(F4)假设

v

→

f

(

v

)=

f

(

v

)+

f

(

v

)，其中

f

和

f

分别是从

D

(

A

)和

C

到

H

的映射，且使得‖

f

(

w

)-

f

(

w

)‖≤

M

‖

A

(

w

-

w

)‖,∀

w

,

w

∈

D

(

A

)，‖

f

(

v

)-

f

(

v

)‖≤

M

‖

v

-

v

)‖,∀

v

,

v

∈

C

，其中：

M

,

M

是正常数.对非线性项

g

(

u

)做以下假设：

2 解的存在唯一性

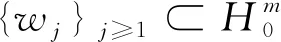
(4)

非线性方程组(4)满足初始条件

其中：1≤

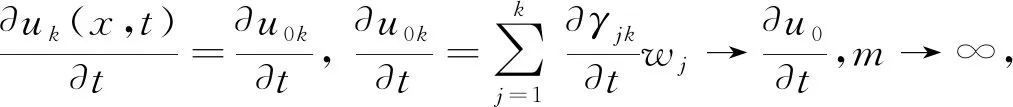
j

≤

k.

显然,上面的有限维时滞系统至少是局部适定的.利用先验估计证明对∀

T

>0，解在每个区间[-

r

,

T

]上是有定义的.

对上式在[0,

t

]上积分,可得

(5)

其中:

C

>0

.

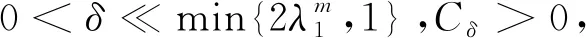
G

(

u

)≤

δ

‖

u

‖+

C

，

则

(6)

其中:|

Ω

|表示空间

Ω

的测度.

(7)

用

t

+

θ

代替上式中的

t

，并利用Gronwall不等式可得

(8)

结合(7)，(8)式可知，对∀

T

>0，有

故

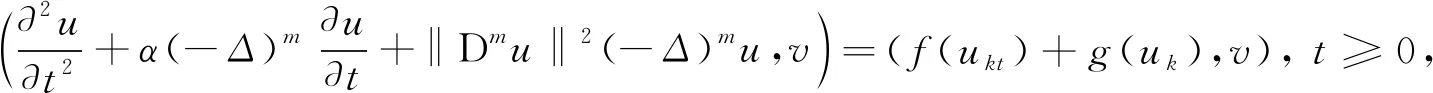
u

是方程(1)在条件(2)，(3)下的解且‖D

u

‖有界.由经典不动点理论可得解的唯一性.

3 惯性流形的存在性

下面证明方程(1)在如下初始条件下惯性流形的存在性

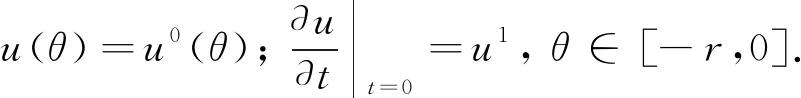
(9)

记

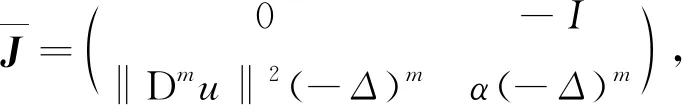
则方程(1)和初始条件(9)可化为

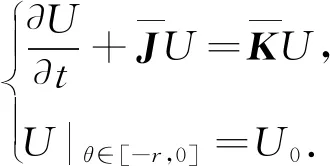
(10)

考虑分解

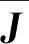
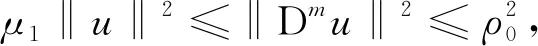
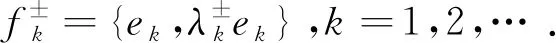
E

=

E

⊕

E

，其中

E

=span{(

e

,0),(0,

e

):

k

=1,2,…,

N

}，

E

=span{(

e

,0),(0,

e

):

k

≥

N

+1}

.E

和

E

的Hermitian内积分别定义为〈

U

,

V

〉=

α

((-

Δ

)

u

,(-

Δ

)

v

)-4(‖D

u

‖(-

Δ

)

u

,

v

)+(

αu

+

u

,

αv

+

v

)，

其中:

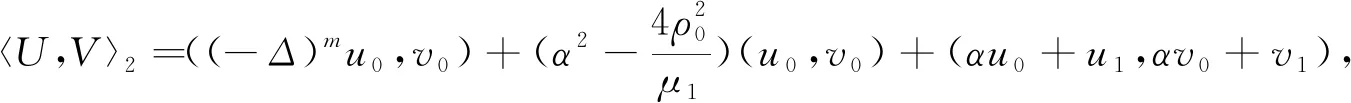
U

=(

u

,

u

),

V

=(

v

,

v

)分别属于相应的子空间

E

,

E

.

对任意的

U

=(

u

,

v

)∈

E

，计算得

(11)

设

P

:

E

→

E

,

P

:

E

→

E

是正交投影.若

U

=(

u

,

v

)∈

E

，

U

=(

u

,

v

)=

P

U

，则

P

U

=

u

,

P

U

=

u

，于是|

U

|=<

P

U

,

P

U

>+<

P

U

,

P

U

>≥

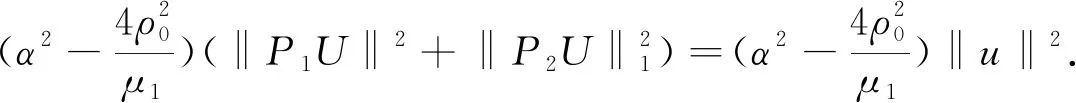
(12)

结合(G1)～(G2),(F1)～(F4)式，有

(13)

其中

(14)

(15)

其中:

U

是(10)式的一个弱解.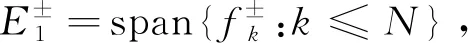

(16)

其中：-

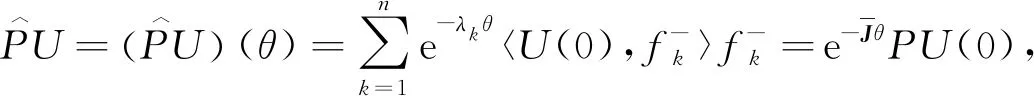
r

≤

θ

≤0，

U

=

U

(

θ

)∈

C

.

假设存在

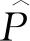
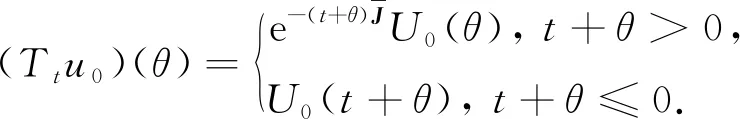
N

，使得谱间隔条件满足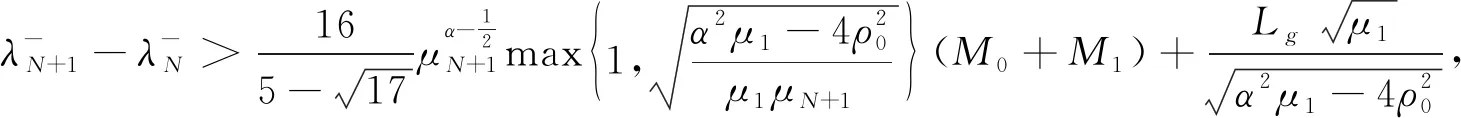

(17)

记

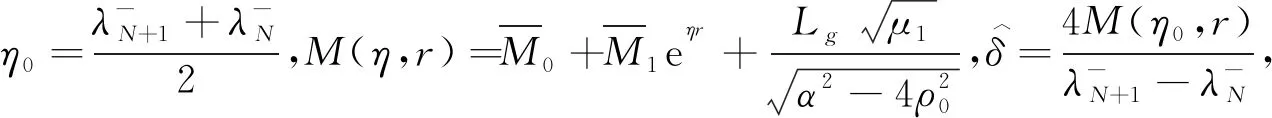
(18)

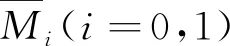
引理2

若谱间隔条件(17)对某一正整数成立且时滞

r

足够小,有

(19)

注

(1)谱间隔条件(17)不包含时滞

r.

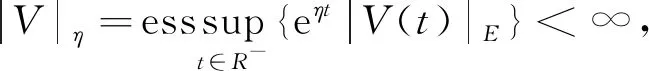
(20)

其中:

η

>0

.

由(13),(16)式可知

(21)

(22)

由(16),(20)～(22)式可得

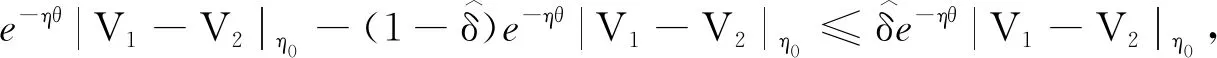
故

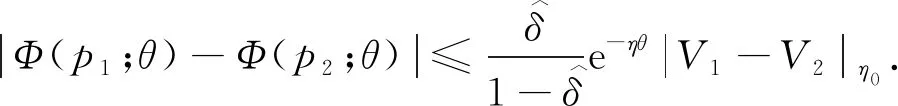
(23)

由(23)式可知,

Φ

满足Lipschitz条件,可以在空间

E

中定义一个流形

μ

，其中

(24)

引理3

由(24)式所定义的流形

μ

关于半群

S

是不变的,即对任意的

t

≥0,有

S

μ

=

μ.

对任一固定的

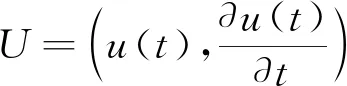
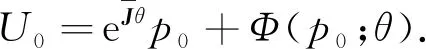
t

>0，定义函数

由于

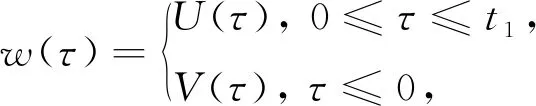
w

(

t

)是问题(10)在

s

≤

t

时的解,由常数变易法可得

(25)

只需证对任意的

s

≤

t

，

w

(

t

)满足如下方程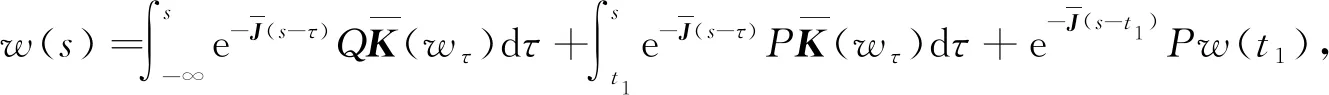

(26)

由

w

(

τ

)的定义可知，当

s

≤

t

时，用

P

作用于(19)式两端,有

(27)

令

s

=

t

，有

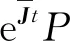
(28)

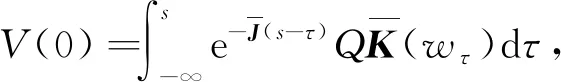
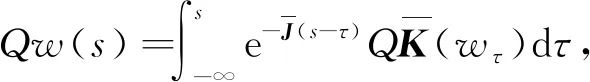
(29)

当

s

≤

t

时,用

Q

作用于(20)式两端,有

由(24)式可知

故当

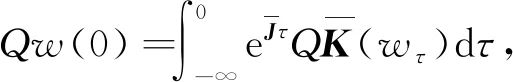
s

≤

t

时,有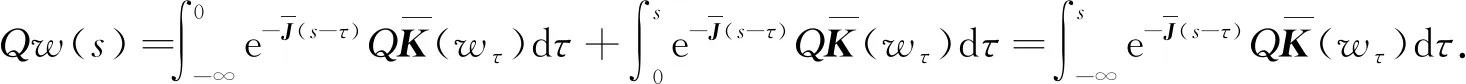

(30)

结合(24),(25)式,可知(21)式成立,这表明

S

μ

⊂

μ.

又由(19)式可知

μ

⊂

S

μ

,故

S

μ

=

μ.

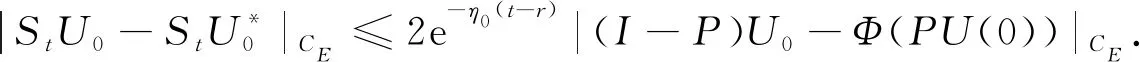
(31)

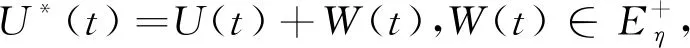
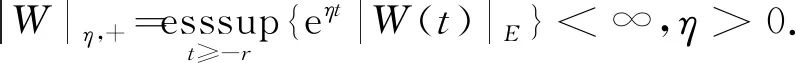
(32)

由于

故当

θ

∈[-

r

,0]时,有

(33)

由于

U

(

t

)∈

μ

，则

(34)

因此

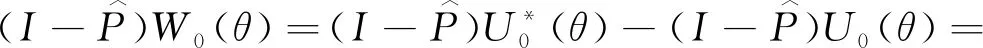
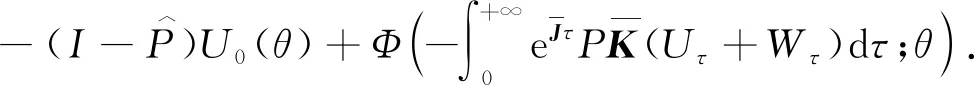
(35)

由(33)，(35)式可得

(36)

|

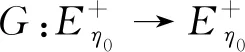
G

(

W

(

t

))-

G

(

W

(

t

))|=|

W

(

t

)-

W

(

t

)|≤

(37)

当

θ

∈[-

r

,0]时,有|

G

(

W

(

θ

))-

G

(

W

(

θ

))|=|

W

(

θ

)-

W

(

θ

)|≤

(38)

于是

因此

类似(37),(38)式可得以下估计

即

于是，结合引理1～4可知带时滞项的高阶Kirchhoff方程(1)及初值条件(9)产生的动力系统在空间

E

中有惯性流形.

即

μ

是问题(10)关于初始值

U

=(

u

,

u

)的惯性流形，且