湖北高密度杉木人工林生长规律研究
袁慧 刘波 陈书杭 朱佳 刘毅 许业洲

摘 要: 為研究湖北省高密度杉木人工林生长规律,对鄂东南地区高密度杉木人工林进行标准地调查,获取61块样地数据和183株解析木数据,建立了杉木单木树高、胸径和材积生长模型,根据拟合优度及残差指标,高密度杉木单木胸径和树高生长的最优模型选择理查德模型,单木材积最优模型选择考尔夫模型,所选模型检验精度均较高,达到拟合效果;通过绘制杉木胸径、树高和材积的生长曲线图,杉木生长量在初始阶段生长速率较大,单木树高和胸径生长量在第4 a达到最大值后逐渐下降,单木材积连年生长量在第10 a达到最大值;利用多元非线性回归建立关于杉木林分平均胸径、平均树高和林分蓄积与林龄、立地指数和林分密度的林分生长模型,选择的林分生长模型均通过检验;利用林分蓄积量的平均生长量和林分平均直径来确定高密度杉木林分的数量成熟龄和工艺成熟龄,在立地指数16~20 m和林分密度4 000~6 000株/hm2时,杉木的数量成熟龄和工艺成熟龄分别为10~13 a、10~11 a,与湖北咸宁地区高密度杉木造林小径级采伐年龄相符。
关键词: 杉木;高密度;生长模型
中图分类号:S718文献标识码:A文章编号:1004-3020(2021)03-0001-08
Growth Regularity of High Density Cunninghamia lanceolata Plantations in Hubei
Yuan Hui(1) Liu Bo(2) Chen Shuhang(2) Zhu Jia(2) Liu yi(3) Xu Yezhou(1)
(1.Hubei Academy of Forestry Wuhan 430075;
2.Xianning Forestry Bureau Qianshan Experimental Forestry Farm Xianning 437100;3.National Nature Reserve of Xingdou Mountain in Hubei Province Enshi 445000)
Abstract: In order to study the growth regularity of high density Cunninghamia lanceolata Plantations in Hubei Province, the authors investigate the high density Cunninghamia lanceolata Plantations in Southeast Hubei Province, obtain 61 sample plots data and 183 analytical wood data, establishe the growth model of the height, DBH and volume of the single Cunninghamia lanceolata. According to the fitting degree and residual index, Richard model is selected as the best model for the growth of the single height and the DBH of the high density, and kolf model was selected as the optimal model for volume growth of single tree. The test accuracy of the selected models was high and the fitting effect was achieved; By drawing the growth curve of DBH, height and volume of Cunninghamia lanceolata, the growth rate of Cunninghamia lanceolata is larger in the initial stage, the growth of single tree height and DBH reaches the maximum in the 4th year and then gradually decreases, and the annual growth of single tree volume reaches the maximum in the 10th year; The stand growth models of average DBH, average height, stand volume, stand age, site index and stand density were established by multiple nonlinear regression; Using the average growth of stand volume and average diameter of stand to determine the quantitative mature age and technological mature age of high-density Cunninghamia lanceolata stand, the quantitative mature age and technological mature age of Cunninghamia lanceolata stand are 10—13 years and 10—11 years respectively when the site index is 16—20 m and the stand density is 4 000—6 000 tree sper hectare, which is consistent with the small diameter age of high-density Cunninghamia lanceolata Plantation in Xianning area of Hubei Province.
Key words: Cunninghamia lanceolata; high density;growth model
杉木Cunninghamia lanceolata是中国特有的速生用材树种,生长快、材质优良、纹理直且具有抵御病虫害能力强等特点,是南方各省区最重要的造林树种之一[1]。中国种植杉木人工林的面积较广,随着杉木经济市场的不断变化,不同规格的杉木材需求量显著增加,小径材也得到广泛利用[2]。
短轮伐期栽培是选用速生树种,采用大密度、集约经营,在短时间内获得最高生物量的一种集约栽培方式,满足木材供应增加的需求[3]。在二十世纪六十年代,美国最早进行了短轮伐期能源林的培育研究,我国最早在八九十年代进行了杨树、桉树等阔叶树种的短轮伐期栽培的良种选育等研究工作,取得了显著成效[4]。于此同时杉木短轮伐期的研究也相继展开,李荣伟等进行杉木林短轮伐期的采伐试验研究[5],通过分析杉木的成熟龄,得出杉木在12~16 a的短轮伐期是合理可行,并提出数学模型。张传峰等对湖南丘陵地区杉木人工林进行研究[6],提出丘陵区杉木林速生期早,但衰退快且生长周期短,宜采取短轮伐期的培育方式。李晓储等对北亚热带江苏南部的低山丘陵区域杉木人工林研究[7],通过拟合林分生长模型,预测出短轮伐建材林的不同立地及林分密度下的适伐年龄,并分析探讨了杉木小径材集约经营和短期轮伐椽材的栽培技术和经济效益[8]。
湖北省位于杉木北缘产区,杉木高密度短周期小径材栽培在鄂东南区已有多年历史,且近年来小径材林的栽培更加广泛,对该区域的高密度造林培育小径材林的杉木林分生长状况进行研究就显得尤为必要。本文利用在湖北省咸宁和黄石等地区获取的高密度栽培杉木人工林标准地调查数据,分析研究小径材杉木单木及林分生长状况,对杉木短周期适伐龄进行研究,为合理缩短杉木用材林生产周期,为杉木小径材的培育及实现其速生丰产经营提供一定的参考依据。
1 材料与方法
1.1 研究地概况
研究材料及数据主要集中在湖北东南部区域,该区域位于北纬29°49′48″~29°50′38″,东经114°19′1.37″~115°13′12″。海拔28~860 m。地势南高北低,由西南向东北呈递减趋势,整体位于大幕山脉北部低山丘陵区。北亚热带气候区,气候温和,四季分明,年平均气温16.8℃,年均日照时数1 825.8 h,年均降雨量1 483.5 mm,年平均无霜期为245~263 d。冬季偏北风,偏冷干燥;夏季偏南风,高温多雨。土壤以红壤和黄棕壤为主。
1.2 数據来源
2016~2017年在湖北省咸宁市和黄石市进行高密度杉木人工林标准地调查,选取不同林龄、不同立地的林分,标准地设置面积为600 m2(20 m × 30 m),样地内每木检尺,测量胸径、树高、枝下高、冠幅等生长量指标,并记录地理位置、造林年度、造林密度等信息。每块标准地中选取3株平均木,按2 m区分段进行树干解析。共调查样地61块,伐取解析木183株。标准地基本信息见表1。
1.3 杉木生长量拟合
单木生长方程选择6个常用的理论生长模型,将解析木分成两组,利用140株建模解析木数据对杉木生长量和年龄进行数据拟合,选出拟合效果最优模型,剩余43株解析木数据用于模型检验。各方程表达式如表2所示,单木拟合及检验数据见表3。
利用每块样地的平均树高和平均胸径作为林分平均生长量,按照样地内每木检尺的林木计算单木材积并推导林分平均蓄积,单株材积利用湖北省杉木二元材积公式计算:V=0.000062678×D1.7043×H1.1486。林分生长模型参考李晓储[7]和李子敬[9]等人研究经验,模型按照表4中方程进行拟合,建模数据及检验数据见表5。
1.4 模型评价与检验
采用判定系数(R2)和标准残差(RSE)指标评价模型的拟合效果[9],从中选出拟合精度最高的方程作为杉木生长模型。
采用平均偏差(ME)、平均绝对偏差(MAE)、平均相对偏差(MPE)、平均相对偏差绝对值(MAPE)和预估精度(p)5个统计量对所选杉木树高、胸径和材积模型进行独立性检验[10]。
1.5 数据处理
利用统计之林ForStat 2.2软件进行解析木树高、胸径和材积计算及模型拟合,SPSS 19.0进行方差分析,应用Excel 2007进行生长模型评价检验计算,利用Sigma Plot10.0作图。
2 结果与分析
2.1 杉木单木生长规律
2.1.1 杉木单木生长模型拟合
以140株杉木解析木作为建模数据,利用6种生长模型分别拟合杉木胸径、树高、材积生长模型,拟合结果如表6所示。
树高和胸径生长模型中,对比各模型的拟合优度及标准残差,其中理查德模型的拟合优度分别为0.829 6和0.829 2,拟合优度最好且标准残差最低,模型参数值也在合理范围内。材积生长模型中理查德模型拟合优度最好(0.829 2),其次为考尔夫模型(0.828 6);理查德模型标准残差值(0.12)略低于考尔夫模型(0.15),但从模型参数值观察,理查德模型材积生长最大值参数a为0.076 7,显然低于杉木材积生长的合理范围。因此杉木树高和胸径生长模型采用理查德模型,而材积生长模型采用考尔夫模型。
利用43株杉木解析木数据对选出的树高和胸径理查德模型及材积考尔夫模型进行检验。模型各检验指标如表7所示。3个模型的预估精度均达到96%以上,其他偏差指标值均相对较小且控制在合理范围内,表明拟合效果符合精度要求。
2.1.2 杉木单木生长规律
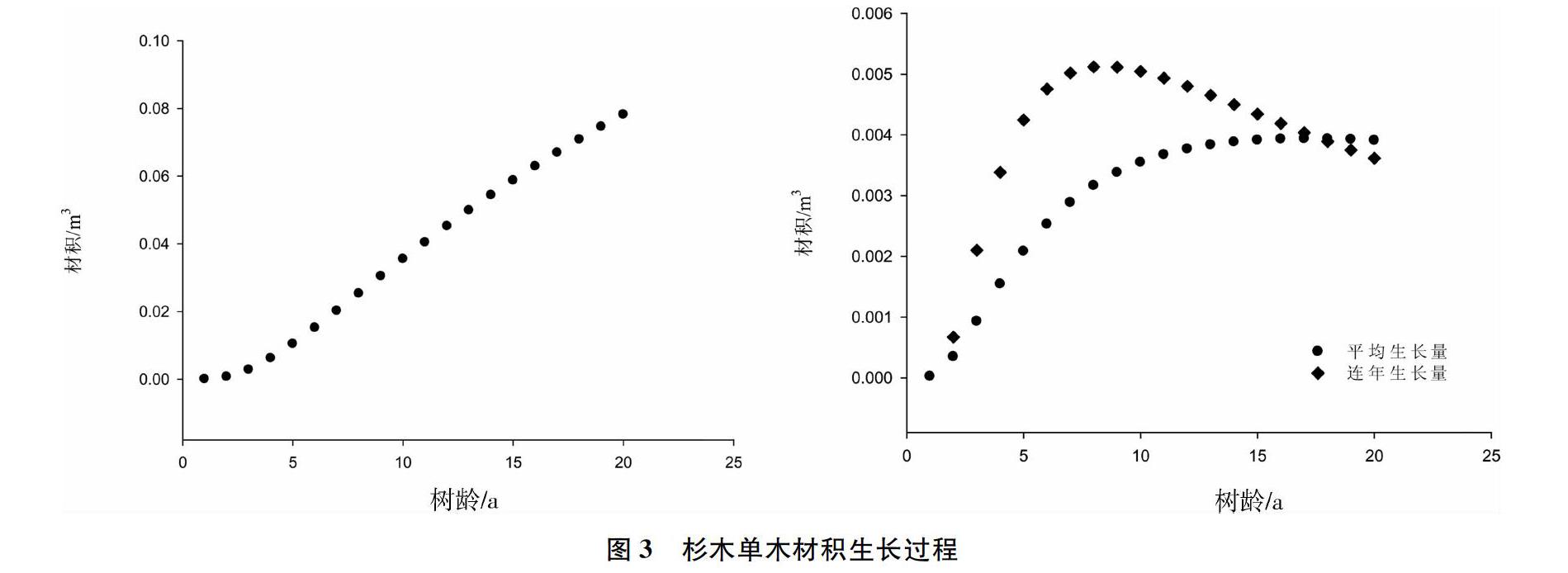
根据拟合得到的杉木最优单木生长模型,计算理论预估值并绘制树高、胸径和材积的平均生长量和连年生长量曲线图(图1~3)。
3个模型的生长曲线均呈“S”形,符合杉木生长的生物学特性。树高和胸径生长曲线的最大值分别趋近于12 m和9 cm,而材积最大值趋近于0.1 m3(图中只显示了前20 a生长情况)。树高、胸径和材积的平均生长量和连年生长量变化趋势大致相同,均呈现最初生长阶段较小且生长速率较大,当生长速率达到最大值后逐渐下降。树高和胸径的连年生长量均在第4 a左右达到最大值,随后逐年减小,树高连年生长量最大值约为1.4 m·a-1,胸径连年生长量约为1.6 m·a-1;而树高平均生长量在第5 a左右达到最大值,约为1.2 m·a-1;胸径平均生长量在第6 a左右达到最大值,约为1.1 m·a-1。因此,树高生长的速生期为生长初期的前5 a,而胸径生长的速生期为生长初期的前6 a。
材积生长速率在初期阶段逐年增加,连年生长量在第10 a左右达到最大值,约为0.008 m3·a-1,随后逐年放缓;而平均生长量在第18 a左右达到最大值,约为0.006 m3·a-1。
2.2 杉木林分生长模型拟合
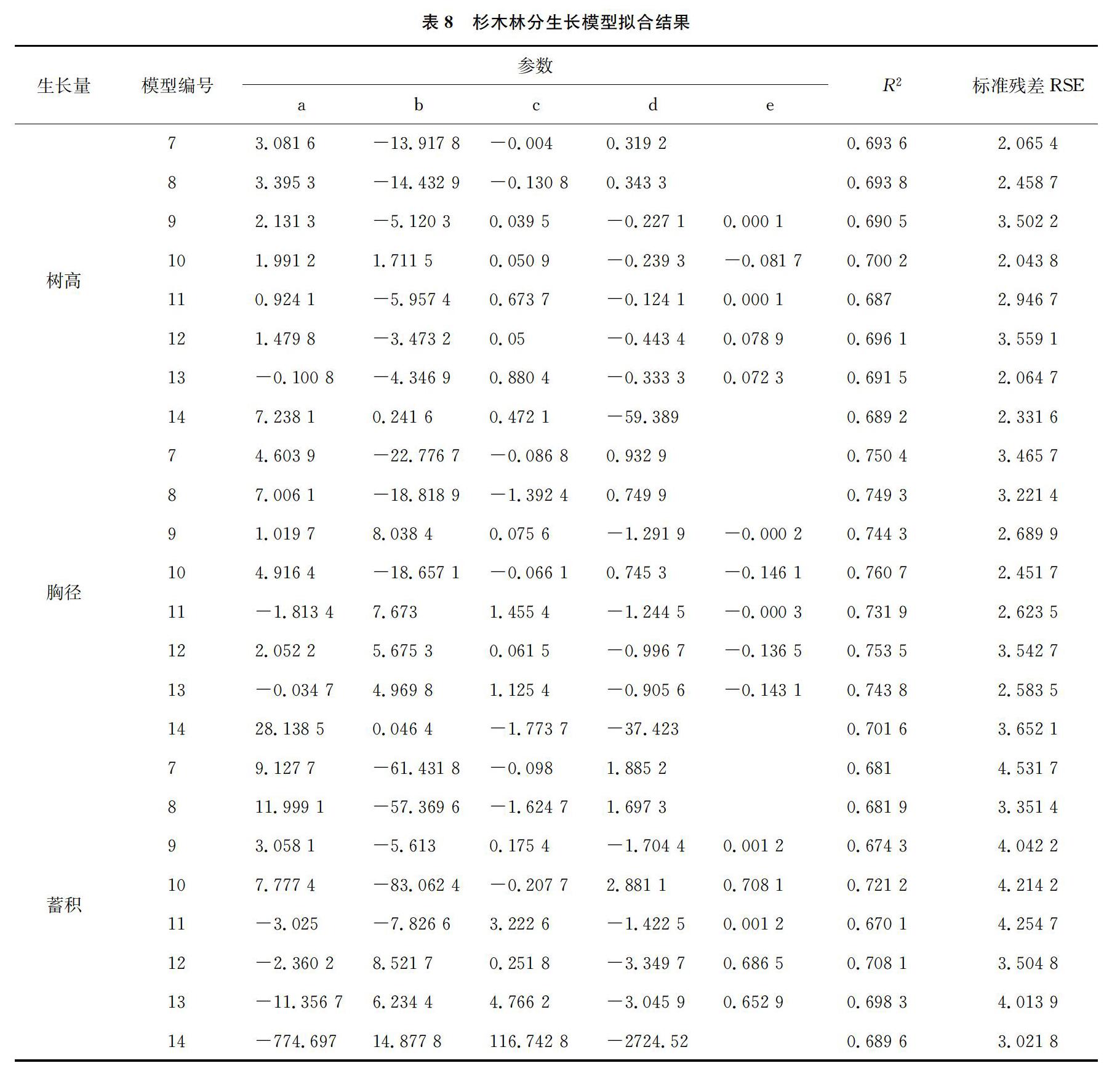
利用表4模型对林分平均树高、林分平均胸径、林分蓄积量分别与林龄、立地指数和林分密度进行拟合,结果如表8所示。从拟合结果表中可以得出林分平均树高、林分平均胸径最优拟合模型为模型10,林分蓄积量的最优拟合模型为模型14,拟合优度分别为0.700 2、0.760 7、0.689 6,拟合优度均高于其他模型;相对应最优模型10和模型14的标准残差在所有模型中最低,分别为2.043 8、2.451 7和3.021 8。因此,对3个选定的最优模型进行检验(表9),模型的相关偏差值均较小且预估精度均达到90%以上,表明模型的拟合效果符合要求。
2.3林分生长量预估与数量、工艺成熟龄
利用拟合得到的最优蓄积量生长模型(模型14),计算不同立地和林分密度条件下林分蓄积量的平均生长量,以平均蓄积生长量最大时对应的年龄确定杉木数量成熟龄[9],并计算对应成熟龄时的林分平均树高和平均胸径(模型10),以林分平均胸径10 cm的林龄为工艺成熟龄。
表10中列出了立地指数14~20 m、林分密度3 000~7 000株·hm-2下林分数量成熟龄及林分平均生长量预估值,数量成熟龄为 10~15 a。数据结果表明,不同立地和林分密度下数量成熟龄均有所不同,同一立地指数不同林分密度下,数量成熟龄随林分密度的增加而减小,林分蓄积年平均生长量随着林分密度的增加而增加,林分平均树高和平均胸径随着林分密度的增加而降低。同一密度不同立地指数条件下,林分数量成熟龄随立地指数的增加而降低,林分蓄积年平均生长量和平均树高随着立地指数的增加而增加,平均胸径随着立地指数的增加而减小。选择立地指数16 m以上、林分密度4 000~6 000株·hm-2的高密度栽培模式林分的数量成熟龄为10~12 a。
表11列出来立地指数14~20 m、林分密度3 000~8 000株·hm-2下林分工艺成熟龄,工艺成熟龄为9~12 a。同一立地指数不同林分密度下,工艺成熟龄随着密度的增加而增加,同一密度不同立地指数条件下,林分工艺成熟龄随立地指数的增加而减小。
在湖北省咸宁地区高密度杉木栽培模式中,造林密度在4 000~6 000株·hm-2,按估算表10、表11可知,该密度下林分达到数量成熟龄在10~14 a,工艺成熟龄在10~11 a。按照咸宁地区小径材杉木市场需求,胸径达到8 cm以上即可出售,综合数量成熟龄及工艺成熟龄,该地区高密度杉木造林第10 a即可达到小径级材的采伐年龄。
3 结论与讨论
利用理论生长方程分别对杉木单木的胸径、树高和材积生长过程进行拟合。最终结果得出,理查德模型是描述高密度杉木单木胸径和树高生长的最优模型,考尔夫模型是单木材积最优模型。根据选定的单木生长方程绘制杉木胸径、树高和材积的生长曲线图,分析了高密度杉木的单木生长规律,树高、胸径和材积的生长量变化趋势在最初生长阶段生长量较小但生长速率较大,生长速率达到最大值后逐渐下降。树高和胸径的连年生长量均在第4 a左右达到最大值,材积连年生长量在第10 a左右达到最大值,李荣伟等人研究四川地区杉木用材林短轮伐期试验[5],树高、胸径平均生长量达到峰值的年龄分别为7 a和8 a,本研究与其比较,生长量达到峰值的年龄提前了3~4 a;与湖北省常规栽培模型杉木人工林单木生长规律相比[11],高密度栽培模型下杉木单木连年生长量达到最大值的时间也均有提前,表明密度对杉木的生长速生期有重要作用,高密度条件下杉木个体竞争会缩短杉木的快速生长期。
根据高密度杉木林分生长模型预估林分数量成熟龄和工艺成熟龄,在立地指数16~20 m时,林分密度4 000~6000株·hm-2培育模式林分数量成熟龄和工艺成熟龄分别为10~13 a、10~11 a,符合湖北咸宁地区高密度杉木造林小径级采伐年龄。同一立地指数下,数量成熟龄随林分密度的增加而减小;同一密度条件下,林分数量成熟龄随立地指数的增加而降低,结果与李晓储等人研究的江苏南部高密度短轮伐杉木建材林的研究结论相符合[7]。本研究仅对杉木的蓄积量成熟龄和工艺成熟龄进行预估,经济成熟龄、生物量成熟龄等指标尚未估算,而杉木短轮伐期成熟龄是由相应的经营目标确定,本研究结果可以为相关杉木短周期经营提供一定参考。
参 考 文 献
[1]施恭明.杉木人工林培育研究进展[J].林业勘察设计,2010,(01):58-60.
[2]王宏棣,何金存,张佳彬.人工林小径结构用材的现状与发展趋势[J].林业机械与木工设备,2007(03):13-15.
[3]郭祥勝.国外短轮伐期人工林的培育[J].林业科技通讯,1989(01):3-5.
[4]郭祥胜.国内外短轮伐期栽培方式研究的现状和趋势[J].林业科技通讯,1988(06):3-5.
[5]李荣伟,王准,刘福云.杉木用材林短轮伐期的试验研究[J].四川林业科技,1987(04):1-8.
[6]张传峰,张玉荣,陈双武.湖南丘陵区杉木短轮伐期高产林试验研究[J].林业科技通讯,1988(12):9-11.
[7]李晓储,黄利斌,范科双,等.苏南低山丘陵杉木短轮伐建材林适伐龄的研究[J].华东森林经理,1997(01):31-36.
[8]李晓储,黄利斌.宁镇扬低山丘陵杉木短轮伐小径材集约经营的探讨[J].江苏林业科技,1987(04):4-8.
[9]李子敬.北亚热带日本落叶松纸浆林最佳轮伐期研究[D].北京:中国林业科学研究院,2011.
[10]李忠国,孙晓梅,陈东升,等.基于哑变量的日本落叶松生长模型研究[J].西北农林科技大学学报(自然科学版),2011,39(08):69-74.
[11]袁慧,杜超群,李斌成,等.湖北省杉木生长模型研究[J].中国农学通报,2019,35(34):50-58.
(责任编辑:唐 岚)

