基于图卷积和全局对齐策略的图分类网络
薛晖 孙伟祥

摘 要:受限于图数据拓扑结构的不规则性,以及图结点的无序性和规模多变性,现有图分类网络往往对结点嵌入向量采取简单聚合或排序等方式来构建图级别的表示向量,这会导致特征过度压缩以及特征平移等问题. 针对这些问题,提出基于全局对齐策略的图卷积网络,通过构建子图特征近似分布将图表示特征向量做全局对齐,在避免过度压缩和特征平移、有效提高下游分类网络对于特征信息挖掘效率的同时,又利用子图特征的分布信息,进一步学习图数据之间内在的结构相似性,从而提升整体网络对于图分类任务的推理能力. 在多个图分类数据集上的实验结果表明,采用全局对齐的图卷积网络相较于其他网络模型有2%~6%左右分类精度的稳定提升,消融实验和超参数敏感性分析实验也进一步证实了全局对齐策略的有效性和鲁棒性.
关键词:图表示学习;图分类;图神经网络;深度学习
中图分类号:TP391 文献标志码:A
Graph Classification Network Based on Graph
Convolutional Network and Globally Aligned Strategy
XUE Hui1,2?,SUN Weixiang1,2
(1. College of Computer Science and Engineering,Southeast University,Nanjing 211189,China;
2. Key Laboratory of Computer Network and Information Integration(Southeast University),
Ministry of Education,Nanjing 211189,China)
Abstract:Limited by the irregularity of graph topology, permutation independence of graph nodes and variability of graph node scale, the majority of neural networks designed for graph classification adopts simple aggregation or sort operation to generate graph-level representation, leading to over-compression and translation of features. In order to address such problems, this paper proposes a novel graph convolutional network, called Globally Aligned Graph Convolutional Network(GAGCN),where graph-level representations are globally aligned by constructing a sub-structural approximate distribution. GAGCN can not only avoid over-compression and feature translation, but also utilize sub-structural distribution to further learn the internal structural similarity among graph data, thereby effectively improving the efficiency of information mining for the downstream classification network and the inference ability for graph classification, respectively. Experimental results show that GAGCN achieves superior results and improves 2%~6% average accuracy on a range of graph datasets,compared with several state-of-the-art graph classification algorithms. The ablation study and the hyper-parameter analysis further reflect the effectiveness and robustness of our approach.
Key words:graph representation learning;graph classification;graph neural network;deep learning
圖数据(Graph-Structured Data)作为一类用于描述实体(点)及实体之间关系(边)的非欧氏数据(Non-Euclidean Data),广泛存在于知识图谱[1]、社交网络[2]、计算机视觉[3]以及生物化学[4]等众多交叉学科领域. 图数据的诸多复杂特性,例如结点的无序性与规模可变性,给现有的机器学习算法带来了巨大的挑战. 幸运的是,近年来,随着深度学习和图表示学习的兴起,DeepWalk[5]、Node2Vec[6]以及图卷积神经网络等算法[7]相继被提出. 特别是图卷积神经网络算法,能够将图数据的拓扑结构特征和结点属性高效地融合,从而学习得到高质量的图结点嵌入表示(Node Embeddings),使得机器学习算法对于复杂图数据的分析和挖掘能力得到了显著提升. 目前,图卷积神经网络算法已经成为机器学习和数据挖掘领域的研究热点之一.
图分类(Graph Classification)作为一类重要的图挖掘任务,旨在对不同类型的图数据进行分类预测. 与结点分类(Node Classification)等任务不同,图分类预测的对象为整个的图数据. 因此,当图神经网络被应用于该任务时,需要对学习得到的结点嵌入向量进行整合转化,生成图级别的表示向量(Graph-Level Representation)后才能用于后续的分类网络[8-9]. 然而,在结点嵌入整合转化生成图表示向量的过程中,存在着以下三个难点: 1)不同图之间结点规模可能存在较大的差异,但整合转化后得到图表示向量维度大小必须统一; 2)图结点的顺序是排列无关且无意义的,但整合转化后得到图表示向量的特征顺序必须是有意义的;3)图数据作为一种信息密集型数据,每个结点都可能代表着一个重要实体,因此结点嵌入中所蕴含的结构特征等信息应当在图表示向量中尽可能保留. 更具体地来讲,前两个难点主要是目前大多数分类算法对于输入数据的特定要求所致,如感知机和神经网络等常用分类器,均要求输入数据的特征尺寸大小必须固定,此外,这些分类器往往不具有处理数据特征排列不变性的能力,即它们对于输入数据的特征排列顺序有一定的要求. 例如,对于图像分类任务,当图像的特征顺序,即像素顺序被打乱后,分类器很可能无法对该图像进行正确分类. 因此,具有明确意义的数据特征顺序对于分类器而言有着至关重要的意义.
对于图分类任务而言,一个理想的特征顺序应当是全局对齐的.即数据的每个特征维度都应该对应着特定的含义. 这一想法是受图像分类任务的启发——该领域的研究者通常采用图像切割和旋转操作进行数据增强[10],以此期望模型学习得到一些不变性,例如平移不变性和旋转不变性,以增强模型对于目标物体的辨别(分类)能力. 究其本质,其需要数据增强的根本原因在于其目标特征没有全局对齐,导致存在特征平移和旋转等现象.若假设目标物体特征是全局对齐的,则这些不变性将没有学习的必要,这会大大降低目标检测难度. 同样地,在图分类任务中,特征不对齐的图表示向量也势必会引入特征平移和旋转等问题,这将对下游的分类网络提出更高的要求. 例如,若分类网络不具备对于特征平移不变性和排列不变性的良好学习能力,那么两个相似图结构很可能会被误认为有较大的差异,从而产生分类误判.
面对这些难点,一部分应用于图分类的网络模型选择牺牲掉图表示向量的信息丰富度,通过简单地将所有结点嵌入进行聚合压缩(求和或平均)的方式,来保证所输出图表示向量的尺寸大小固定,以及避免特征顺序的困扰[9,11-12]. 此外,还有一些模型对结点嵌入向量通过给定的规则排序后,固定地取前k个,然后将其拼接得到图表示向量[13]. 此类方法可以通过调节超参数k使得特征信息丢失减少,但是其得到的图表示向量的特征顺序仅是局部对齐的,无法避免特征平移等现象,且后续的分类网络并不能保证完全学习到这些不变性. 对于该方法而言,整体模型的分类性能将受到分类网络对于平移不变性学习的严重制约.
为了避免现有模型的这些缺陷,本文提出了一个新颖的图神经网络模型,即全局对齐图卷积网络(Globally Aligned Graph Convolutional Network,GAGCN),用于图分类任务. GAGCN通过新颖的全局对齐层(Globally-Aligned Layer)的设计,使得模型能够学习到全局特征语义对齐,且具有丰富结构信息的图表示向量,以此提高模型对图分类任务的分类精度. 具体地,GAGCN对于图分类任务的处理主要包含以下3個步骤: 1)图卷积网络学习得到图数据的结点嵌入向量;2)通过对结点嵌入空间做切片,得到子图(Subgraph) 特征的近似分布,并以此生成特征顺序全局对齐的图表示向量; 3)将图表示向量送入分类网络进行分类预测. 在多个数据集上的实验结果表明,GAGCN在图分类任务上的表现要优于各类比较算法,进一步的消融实验和敏感性分析实验也验证了GAGCN全局对齐策略的有效性以及鲁棒性.
1 相关工作
1.1 图核(Graph Kernel)
GAGCN的主要思想是受两类图核方法所启发,即WL-Subtree Kernel算法[14]以及Graphlet Kernel
算法[15]. 其中, WL-Subtree Kernel通过Weisfeiler -Lehman算法得到图中以每个结点为根结点的子树的特征集合后,通过比较两个图中子树结构特征的分布,计算得到两个图之间相似度. 而Graphlet Kernel算法则通过比较两个图数据的图元分布来计算它们之间的相似性. 受这两个工作的启发,本文提出通过构造子图特征的近似分布来对齐图表示向量的特征顺序,从而使得模型能够更轻易地学习和衡量不同图数据之间的相似性以及差异性. 但与这两个方法不同的是,GAGCN是基于图神经网络搭建的图分类模型,因此具有更强的特征抽象能力和更高的可扩展性.
1.2 图卷积神经网络
受传统卷积神经网络在图像处理领域获得巨大成功的激励,许多研究者尝试将卷积网络引入图领域,并提出了众多图卷积神经网络模型[16-19]. 总体来说,这些模型可以分为基于频谱(Spectral-Based)的方法和基于空间(Spatial-Based)的方法两大类. Xu等人[9]为大多数现有的图神经网络抽象出了一个统一的架构. 在该架构中,第k层图卷积被描述为:
ak
u = ψ({zk-1
u :v∈H(u)})
zk
u = φ(zk-1
v ,ak
u)
式中:zk
u 代表第k层学习得到的结点u的嵌入向量;H(u)为结点u的邻接点构成的集合;ψ(·)与φ(·)分别为聚合函数和结合函数,前者用来学习邻域结点的结构信息,后者将邻域信息与结点自身信息相融合. 当图神经网络用于图分类任务时,需要将这些结点嵌入向量整合转换为整个图的表示向量. 一些图神经网络模型通过将结点嵌入向量简单地进行聚合[9,11-12,20],例如求和或均值等,做生成图表示向量. 此类方法是受图像分析算法,特别是卷积神经网络中全局池化操作(Global Pooling)的启发,其特点是简单易实现,通过加入简单的聚合操作就可以将图卷积神经网络用于图分类任务. 但是图与图像不同,图像的多数像素可能都是背景和噪声信息,而图的每个结点都对应一个重要实体,故图的有效信息密度远高于图像,因此这类聚合策略由于过度压缩特征,有时会造成不可承受的信息损失. Zhang等[13]为了避免这一情况,提出了基于排序的全局池化方法,用于结点嵌入到图表示向量的转换,但是该方法却又引入了特征平移等问题. 此外,还有一些研究者提出采用集合学习(Set Learning)的方法,例如Set2Set[21],DeepSet[22]等,用于生成图表示向量[8],然而这些方法在带来大量计算开销的同时,其提升效果并不显著. 另外,针对图数据的对齐问题,AVCN[23]提出在图数据预处理层面采用任意图到平面图转换的技术来对齐图结构,但该转换过程并非是无损的,因此在数据预处理层面就可能造成了一些信息损失,且AVCN仅考虑了图数据的结点属性,忽略了一些边的信息,这些因素使得该模型对于图数据结构特征的学习能力可能不如一般图卷积神经网络,因此在图分类任务上得到的提升效果有限.
2 全局对齐图卷积网络
本文提出的全局对齐图卷积网络(GAGCN)遵循三段式架构:首先,图卷积层得到结点嵌入向量;其次,全局对齐层生成图表示向量;最后,由分类网络进行分类预测.
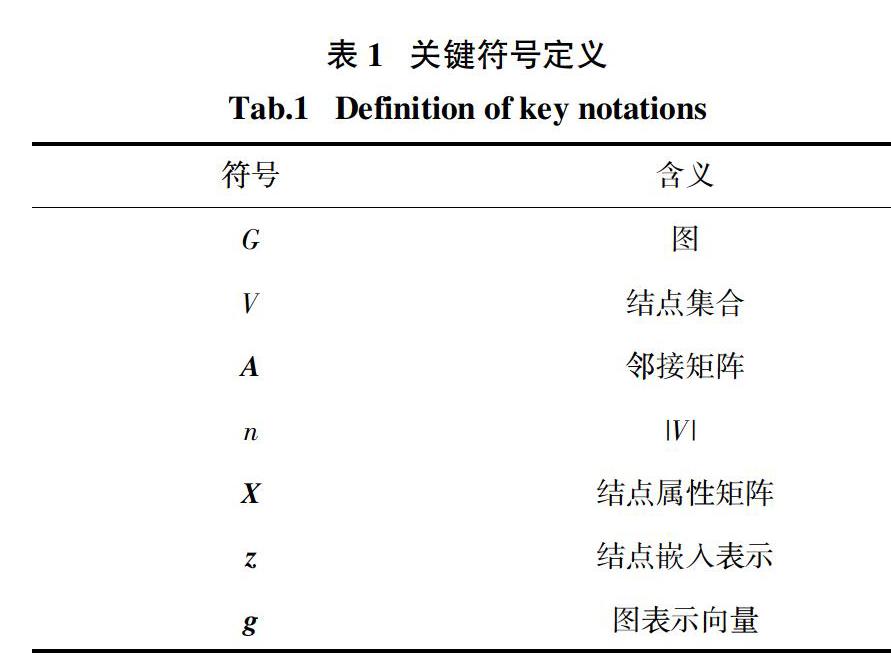
2.1 符号定义
关键符号及其含义如表1所示. 此外,本文还约定X∈Rn × d,其中矩阵X第u个行向量表示结点u的属性;zk
u ∈Rck
表示第k层图卷积输出的结点u的嵌入向量,且向量维度为ck . Zk∈Rn × ck
表示第k层图卷积网络输出的图G所有结点嵌入向量构成的结点嵌入矩阵.
2.2 图卷积神经层
GAGCN定义新的图卷积算法如下:
Hk = [D][~]-1/2 [A][~][D][~]-1/2·F(Zk-1) (1)
Zk = σ(Hk + μZk-1W) (2)
式中:[A]= A + I,表示圖G每个结点加了自环(Self-Loops)后的邻接矩阵;[D] 表示[A] 的度数矩阵(为对角矩阵);当k = 0时采用Z0 = X;F(·)是为进一步抽象结构特征而设计的一个轻量级全连接网络;W为一个可学习的参数矩阵;μ为融合时的平衡系数,融合后得到的特征通过一个激活函数σ(·)来做非线性变换,最终得到第k层所有结点嵌入向量,即Zk. 式(1)的目的是学习给个结点周围邻域的结构信息,式(2)是将邻域信息与结点自身信息做融合.
GAGCN通过堆叠加深图卷积层来提高模型对结点嵌入向量的学习能力. 但值得注意的是,与传统卷积神经网络模型类似,随着卷积层数加深,每一个神经单元的感受野也会不断扩增,故不同图卷积层得到的结点嵌入实际上蕴含结点周围不同规模的子图特征信息,即第一层得到一阶邻域子图特征,第二层得到二阶邻域子图特征等等,以此类推. 然而,堆叠深度过深会使得深层卷积层所学习的所有结点嵌入向量产生趋同性,该现象被称之为过渡平滑(Over-Smoothing)[7]. 因此,不宜采用过深的网络结构来学习结点嵌入表示. 同时,这一点也表明,对于图分类任务而言,需要综合考虑各层的结点嵌入输出,才能多方位地衡量图数据中各个领域规模的子图特征信息,以提高模型对图数据整体的学习能力.
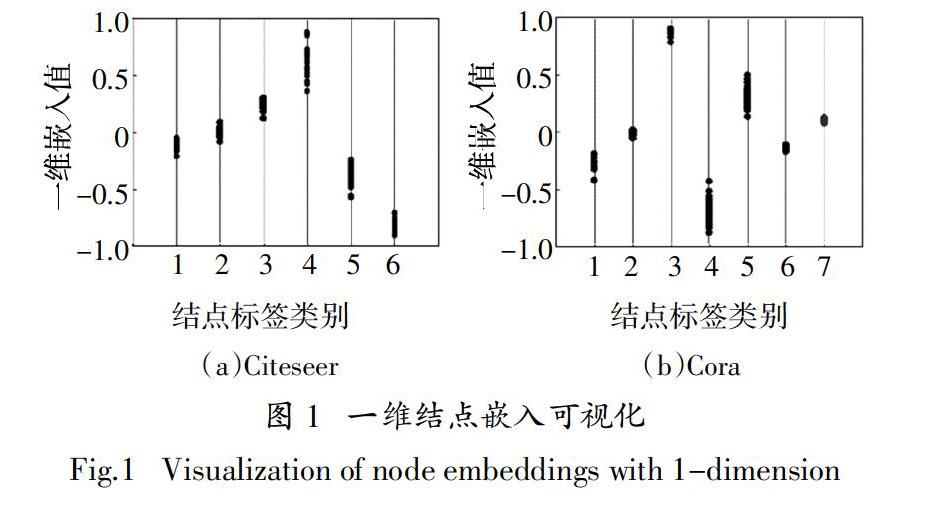
进一步分析,图卷积网络作为Weisfeiler-Lehman算法的一个“软版本”(Soft Version)[13,24],其学习得到的结点嵌入向量可以被认为是“连续的色彩”(Continuous Color),而“色彩”在Weisfeiler-Lehman算法中被用来表示不同的子图特征. 因此,图卷积层学习得到的结点嵌入本质上也可以被看作是一种子图特征的连续向量表示形式. 此外,文献[13]指出,图卷积网络可以将相似的结构特征嵌入至距离相近的向量中进行表达. 基于以上两点,可以得到一个基本的论断,即通过图卷积网络学习得到的距离相近的结点嵌入向量蕴含着相似的子图结构信息. 为进一步验证本小节提出的图卷积网络是否符合该论断,本文在Cora和Citeseer两个常用的结点分类数据集上进行了验证. 该验证建立在这样一个合理假设的基础上,即两个带有相同标签的结点,其邻域结点构成的子图的相似性,要大于两个带有不同标签的结点. 结点嵌入可视化结果如图1所示,图中每个点代表一个结点嵌入,不同的横坐标代表不同的结点标签. 从图中可以清晰地看到,即使是将结点嵌入维度压缩到了一维,带有相同标签的结点嵌入仍然表现出了强聚类特征. 因此,可以认为本节提出的图卷积网络符合结点邻域结构越相似,学习得到的结点嵌入表示距离越相近这一特性.
2.3 全局对齐层
图卷积网络得到结点嵌入表示向量后需要整合转化为整个图的向量表示,才能交由分类网络进行分类. 前文提及了该过程的几个难点所在,即如何保证图表示向量在维度大小固定以及特征顺序有意的前提下,尽可能地保留更多的结构信息. 为了解决这些问题,本文提出了全局对齐层(Globally-Aligned Layer),其通过构建子图特征的近似分布来全局对齐表示特征的语义,能够有效地提高图神经网络方法在图分类任务上的性能. 本小节将详细介绍Globally-Aligned Layer的原理与定义.
首先假定,在Globally-Aligned Layer中能够定义U∈Rk × r,其中U的每一个行向量Ui表示特定类型子图的特征,则U能够满足特征全局对齐性的同时,还能够反应出子图特征的分布信息. 为了做到这一点,需要确切地给出Ui的具体定义. 在2.2节的讨论中,可以发现式(1)与式(2)所定义的图卷积网络学习到的结点嵌入向量,实际上表示的是子图的特征,且满足距离越相近,所蕴含的子图信息越相似的性质. 因此,可以通过统计结点嵌入向量的分布来间接统计子图特征的近似分布. 更具体地,通过将结点嵌入的表示空间
,a+i
用来表示 Pi,且Ui被定义为:
Ui = ψ({zl
u ∶ zl
u∈Pi,?u∈V}) (3)
从而得到U = [U1,U2,…,Uκ]T. 此处ψ(·)表示将属于Pi的所有结点嵌入进行聚合. 由于Pi内的结点嵌入距离相近,故其所表达的子图特征具有相似性,因此此处的聚合不会因为压缩而造成特征信息的过度损失.
进一步,为了将所有共l层图卷积网络所习得的结点嵌入充分利用,对于?u∈V,定义
hu = [zl
u,z l-1
u ,z l-2
u ,…,z 1
u] (4)
式中:hu表示将所有图卷积层的输出拼接. 式(3)重写为:
Ui = ψ({hu ∶ hu
1∈Pi,?u∈V}) (5)
重写后U∈Rk × r,其中r = ci . 为了增加图表示向量的伸缩性,控制表示向量的维度,Globally-Aligned Layer采用一个可学习的线性变换矩阵Ws∈Rr × m(m < r)来做最后的变换,得到最终的图表示向量:
g = f(U·Wf) (6)
f(·)函数的意义为将输入矩阵拉伸为向量形式. 式(6)还可以被等价地看作对U逐行做卷积核为1、步长为1且通道数为m的一维卷积,故其不仅可以伸缩图表示向量维度,还能够起到归纳整合U中每个行向量Ui所蕴含的结构特征信息的作用.
进一步分析,根据R-Convolution理论[25],两个图之间的相似度被定义为:
D(G,G′) = δ(s·s′) (7)
式中:S和S′分别为G和G′的子图结构集合;δ(s·s′)=1当且仅当s和s′同构或近似同构,否则δ(s·s′)=0. 该理论说明,通过对比两个图数据的子图分布,可以计算得到它们近似同构的子图对数,进而推断出图数据之间的相似性. 事实上,许多图分类算法都是基于该原理[14-15]. 因此,Globally-Aligned Layer生成的图表示向量所蕴含的子图特征分布信息,有助于模型挖掘图数据之间内在的结构相似性,能够以此对图数据进行更为合理的分类推断.
2.4 分类网络与损失函数
为了说明GAGCN生成的图表示向量不存在特征平移,且蕴含信息易被挖掘,故GAGCN采用单隐藏层的简单全连接网络作为分类器. 最后,SoftMax和交叉熵(Cross-Entropy)被用来计算分类损失.
3 实验结果与分析
本节共包含3个实验: 1)基准实验通过将GAGCN与多个主流图分类算法在7个常用图数据集上进行比较,来评价GAGCN模型在图分类任务上的整体表现; 2)消融实验通过对全局对齐层的消融替换,来证明全局对齐层策略的有效性;3)参数敏感性分析实验用来进一步验证GAGCN的鲁棒性.
本节所涉及的所有实验均基于Ubuntu Linux 16.04操作系统,GAGCN源码使用PyTorch 和PyTorch-Geometric[26]学习框架实现,程序运行时的硬件环境为i7-8700K CPU、32GB RAM以及TITAN RTX GPU.
3.1 基准实验
数据集.该实验共采用7个常用图分类数据集,涵盖了生物、化学以及社交网络三个研究领域:在PROTENS、DD以及ENZYMES这3个数据集中,每个样例都代表一个蛋白质分子或酶分子;NCI-1中不同样例代表了不同的化学分子结构;IMDB-B、IMDB-M以及REDDIT-MULTI-12K(下文简写为RED-M12K)则是由社交或关系网络组成的图数据集合. 其中,生物、化学领域的4个数据集中每个图结点都带有属性;而社交网络的3个数据集则不带有结点属性,为了实验比较的公平性,GAGCN参照其他对比算法,将结点的度数作为其属性. 数据集相关的其他几个关键参数在表2中有详细的量化说明.
比对算法. 该实验选取的对比算法包括2个与GAGCN相关的Graph Kernel算法,以及5个主流的基于深度学习的图分类算法. 具体介绍如下.
Graph Kernel对比算法:即前文提及的WL-Subtree Kernel以及Graphlet Kernel两个算法. 当计算得到核矩阵之后,实验采用软间隔支持向量机(C-SVM)[27]对其进行分类. 该实验选取这2个Graph Kernel算法作为对比,主要是考虑到其与GAGCN理论上的相似性,故存在比较的意义和价值.
基于深度学习的对比算法:
1)DGK[28] [KDD,2015],即Deep Graph Kernel. 该方法通过CBOW以及Skip-Gram等模型学习得到子图结构之间的依赖性,从而提高经典Graph Kernel的分类性能.
2)DGCNN[13] [AAAI,2018]. 该模型提出了Sort-Pooling層,将结点嵌入按照其表示的子结构来进行排序,从而得到局部对齐的图表示,最后通过卷积神经网络进行分类.
3)DiffPool[29] [NeurIPS,2018]. 该算法实现了一个可微分的图池化方法,帮助图神经网络模型更好地处理图分类任务.
4)GIN[9] [ICLR,2019]. 该模型主要探究了不同的图卷积聚合算子对图分类任务的影响. 表2中GIN-0和GIN-为GIN模型的不同的实现.
5)CapsGNN[30] [ICLR,2019]. 该算法将胶囊网络(Capsule Networks)概念迁移至图领域,提出了胶囊图神经网络用于图分类任务.
GAGCN架构及参数设置:GAGCN的整体架构如图2所示. 在该实验中,各模块具体的参数设置如下:对于图卷积模块,其共包含6层图卷积,前5层通道数设置为64,最后一层设置为1,并均使用tanh作为非线性激活函数,式(1)中的F(·)被设计为具有64个隐藏神经元的简单全连接网络,且隐藏层采用ReLU进行非线性激活;对于全局对齐层,设超参数κ = 50,m = 32即Ws∈R321 × 32;对于分类网络,设其为具有128个隐藏神经单元的全连接网络,为了降低过拟合的风险,在该隐藏层后采用了Dropout,且Dropout rate为0.5. 最后,SoftMax和交叉熵被用来计算分类损失,整个模型可以做到端到端(End-to-End)训练以及分类预测. 此外,GAGCN的训练采用带有动量的随机梯度下降算法[31],且动量参数momentum为0.9. 对于不同的数据集,学习率从{0.01,0.001}中进行搜索,且用于小批次训练的超参数Bacth为64. 与对比算法相同[9,29],实验使用Early-Stopping技术,当判断损失函数不再下降,或精度不再提升时停止训练.
对比算法参数设置:对于WL-Subtree Kernel算法,其迭代次数搜索范围为{1,2,3,4,5};对于Graphlet Kernel算法,为了保证其计算效率,图元的结点规模被限定为3个结点以内. 当C-SVM进行分类时,其软间隔超参数C在{10-3,10-2,…,102,103}中进行搜索. 这两个算法运行坏境为MATLAB,C-S采用LIBSVM库实现. 对于5个基于深度学习的对比算法,表2报告了其原论文中的实验结果. 如果在原论文中某些数据集的结果没有被报告,则采用其官方源码对其进行补充实验,超参数设置遵循原论文和官方源码中的指导规则进行调整搜索. 对DGK而言,由于没有找到可用官方源码,故在DD数据集上没有参与比对. 所有对比算法,包括GAGCN,均使用十折交叉验证(10-Fold Cross-Validation )进行实现,表2中报告的分类精度为十折交叉验证精度的平均值.
由表2可知,在7个图分类数据集上,GAGCN相较于表现最好的对比算法平均精度将近有2%的显著提升. 尤其在PROTEINS、IMDB-B、ENZYMES以及RED-M12K几个数据集上有1%~4%的提升. GAGCN和DGCNN都强调避免结构信息的损失,提高图表示向量的信息丰富度,但是由于DGCNN只做到了特征局部对齐,而GAGCN则是利用子图特征分布做了全局对齐,同时使用了更为强大的图卷积网络,故在所有数据集上,GAGCN均好于DGCNN. 此外,GIN的分类结果也不如GAGCN,GIN虽然使用了同样强大的图卷积网络来做结点嵌入,但是却采用了简单聚合的方法来学习图表示向量,过度压缩了结构特征,造成信息损失,这一对比结果也进一步证明了GAGCN研究动机的合理性. 相较于DiffPool、CapsGNN等其他主流的图分类模型,GAGCN也体现了非常高的竞争力. 与基于Graph Kernel的两个方法相比,尽管WL-Subtree Kernel 在NCI-1数据集上取得了最好的结果,但GAGCN在NCI-1上的表现也同样亮眼,并且在其他6个数据集上的分类精度都显著高于这两个方法. 值得注意的是,Graphlet Kernel和GAGCN虽然都是利用了子图分布这一想法,但是结果却相差较多,这也说明了图神经网络模型在图分类任务上的优越性.
3.2 消融实验
为进一步证明GAGCN的关键贡献,即全局对齐策略的有效性,本文针对Globally-Aligned Pooling进行了消融实验. 该实验通过对GAGCN架构的Globally-Aligned Pooling做替换,并测试替换后的模型在NCI-1、DD、PROTEINS、IMBD-B以及ENZYMES等几个数据集上的分类表现,来比较不同的图表示向量生成策略对图分类结果的影响. 该实验共测试了5种图表示向量生成策略,包括两种聚合策略(Sum-Pooling和Average-Pooling)、Sort-Pooling、Set2Set以及本文提出的Globally-Aligned Pooling. 对于Sort-Pooling的超参数设置,实验遵循DGCNN论文及其源码的指导原则,并考虑到该策略对分类器的特殊要求,分类网络同样也与DGCNN的设置保持相一致;对于Set2Set,其迭代次数在{1,2,3}中搜索最优参数设置.
實验对比结果如图3所示,本文提出的Globally-Aligned Pooling在这些数据集上都取得了最高的分类精度. 再进一步分析,可以看到Globally-Aligned Pooling和Sort-Pooling,相较于聚合策略而言,分类精度较高,这一点证明了尽可能多地保留结构信息确实有助于提高模型的分类表现. 而Globally-Aligned Pooling和Sort-Pooling两者的比较结果也证明了全局对齐策略确实能够帮助后续的分类网络更好地利用和学习图表示向量的特征,从而更容易帮助模型挖掘出一些有价值的信息,帮助分类网络更好地进行分类. 此外,Set2Set这类集合学习的策略由于其本质上是基于聚合操作的一类加权求和策略,其权重的计算基于LSTM和注意力机制,在引入这些额外的计算复杂度的同时其结果也没有得到稳定的提升. 综上所述,该消融实验证明一个优秀的图表示向量生成策略需要保留足够丰富的特征信息,且全局对齐的特征顺序能够有效地提高图神经网络在图分类任务上的精度,进一步证明了本文提出的全局对齐策略的有效性.
3.3 超参数κ敏感性分析
κ作为Global-Aligned Layer的关键超参数,可能会对模型的预测结果产生关键性的影响. 因此,为了评估κ的参数取值敏感性,以及探究其有效的取值范围,本文针对超参数κ进行了敏感性分析实验. 该实验设定κ取值为{10,20,30,50,70,100,200},其他超参数采用与3.1节相同的设置. 如图4所示,在DD和PROTEINS两个数据集上,模型的分类精度呈现出一开始随着κ值的增加而提高的趋势,这是因为当κ值过小时,子图特征近似分布粒度较粗,特征被压缩较多,随着取值不断增大图表示向量蕴含越来越多的结构细节信息,这有助于模型更加合理地进行推断预测. 然而,当到达一定阈值之后,分类精度出现轻微的下降,虽然趋势不明显,但也反应出若取κ值过高或会承担一定过拟合的风险. 而在IMDB-B数据集上,GAGCN分类精度总体随κ值的增加而提高,但当超过一定阈值后,这一增加的趋势也变得不明显. 从该实验结果的分析中不难发现,κ值的取值会对结果产生一定的影响,但是总体来说,κ并不是一个取值非常敏感的超参数,在这3个数据集上,κ取值范围在50左右时,可以认为取得较为稳定且不错的结果.
4 结 论
针对现有图神经网络生成图级别表示向量时,存在的过度压缩和特征平移等问题,本文提出了基于全局对齐策略的图卷积网络,即GAGCN,该网络通过构建子图特征的近似分布来对齐图表示向量的特征顺序,在避免特征平移问题的同时,保留了更为丰富的结构特征信息,且GAGCN生成的图表示向量中蕴含的子图特征分布信息,能够帮助后续分类网络更容易地挖掘数据间内在的结构相似性,从而提高模型在图分类任务上的分类精度.
参考文献
[1] WANG Q,MAO Z D,WANG B,et al. Knowledge graph embedding:a survey of approaches and applications[J]. IEEE Transactions on Knowledge and Data Engineering,2017,29(12):2724—2743.
[2] YING R,HE R N,CHEN K F,et al. Graph convolutional neural networks for web-scale recommender systems[C]//Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York,USA:ACM,2018:974—983.
[3] LONG J W,FENG X,ZHU X F,et al. Efficient superpixel-guided interactive image segmentation based on graph theory[J]. Symmetry,2018,10(5):169—190.
[4] GOKCCER Y,DEMIRCI M F,TAN M. A graph-based pattern recognition for chemical molecule matching[C]//International Conference on Bioinformatics Models. Setubal,Portugal:SciTe Press,2015:158—162.
[5] PEROZZI B,AL-RFOU R,SKIENA S. DeepWalk:online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining- KDD. New York,USA:ACM,2014:701—710.
[6] GROVER A,LESKOVEC J. Node2vec:scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York,USA:ACM,2016:855—864.
[7] ZHOU J,CUI G,ZHANG Z,et al. Graph neural networks:a review of methods and applications [EB/OL]. [2020-04-30]. https:// arxiv.org/abs/1812.08434.
[8] NAVARIN N,TRAN D V,SPERDUTI A. Universal readout for graph convolutional neural networks[C]//2019 International Joint Conference on Neural Networks(IJCNN). Budapest,Hungary:IEEE,2019:1—7.
[9] XU K,HU W H,LESKOVEC J,et al. How powerful are graph neural networks?[EB/OL]. [2020-04-30]. https://arxiv.org/abs/1810.00826.[10] BUSLAEV A,IGLOVIKOV V I,KHVEDCHENYA E,et al. Albumentations:fast and flexible image augmentations[J]. Information,2020,11(2):125—145.
[11] DUVENAUD D,MACLAURIN D,AGUILERA-IPARRAGUIRRE J,et al. Convolutional networks on graphs for learning molecular fingerprints[EB/OL]. [2020-04-30]. https://arxiv.org/abs/1509.09292.
[12] DEFFERRARD M, BRESSON X, VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering[C]//Annual Conference on Neural Information Processing Systems. Cambridge,MA,USA:MIT Press,2016:3837—3845.
[13] ZHANG M,CUI Z,NEUMANN M,et al. An end-to-end deep learning architecture for graph classification[C]//AAAI Conference on Artificial Intelligence. Menlo Park,CA,USA:AAAI Press,2018:4438—4445.
[14] SHERVASHIDZE N,SCHWEITZER P,VAN LEEUWEN E J,et al.Weisfeiler-Lehman graph kernels[J]. Journal of Machine Learning Research,2011,12:2539—2561.
[15] SHERVASHIDZE N,VISHWANATHAN S V N,PETRI T,et al. Efficient graphlet kernels for large graph comparison[C]// International Conference on Artificial Intelligence and Statistics. Cadiz,Spain:JMLR,2009:488—495.
[16] KIPF T N,WELLING M.Semi-supervised classification with graph convolutional networks[EB/OL].[2020-04-30]. https://arxiv.org/abs/ 1609.02907.
[17] LI R,WANG S,ZHU F,et al. Adaptive graph convolutional neural networks[C]//AAAI Conference on Artificial Intelligence. Menlo Park,CA,USA:AAAI Press,2018:3546—3553.
[18] XU D,RUAN C W,MOTWANI K,et al. Generative graph convolutional network for growing graphs[C]//ICASSP 2019-2019 IEEE International Conference on Acoustics,Speech and Signal Processing (ICASSP). Brighton,United Kingdom:IEEE,2019:3167—3171.
[19] BECK D,HAFFARI G,COHN T. Graph-to-sequence learning using gated graph neural networks[C]//Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics(Volume 1:Long Papers). Melbourne:Association for Computational Linguistics,2018:273—283.
[20] ATWOOD J,TOWSLEY D. Diffusion-convolutional neural networks[C]//Annual Conference on Neural Information Processing Systems. Cambridge,MA,USA:MIT Press,2016:1993—2001.
[21] VINYALS O,BENGIO S,KUDLUR M. Order matters:sequence to sequence for sets[EB/OL].[2020-04-30]. https://arxiv.org/abs/1511.06391.
[22] REZATOFIGHI S H,BGV K,MILAN A,et al. DeepSetNet:predicting sets with deep neural networks[C]//2017 IEEE International Conference on Computer Vision(ICCV). Venice,Italy:IEEE,2017:5257—5266.
[23] BAI L,CUI L X,WU S,et al. Learning vertex convolutional networks for graph classification[EB/OL]. [2020-04-30]. https://arxiv.org/abs/ 1902.09936.
[24] MORRIS C,RITZERT M,FEY M,et al. Weisfeiler and leman go neural:higher-order graph neural networks[J]. Proceedings of the AAAI Conference on Artificial Intelligence,2019,33:4602—4609.
[25] DAVID H. Convolutional kernels on discrete structures[R]. Santa Cruz,USA:Computer Science Department,University of California,1999:UCSC-CRL-99-10.
[26] FEY M,LENSSEN J E. Fast graph representation learning with pytorch geometric[EB/OL]. [2020-04-30]. https://arxiv.org/abs/1903.
[27] CORTES C,VAPNIK V. Support-vector networks[J]. Machine Learning,1995,20(3):273—297.
[28] YANARDAG P,VISHWANATHAN S V N. Deep graph kernels[C]//Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York,USA:ACM,2015:1365—1374.
[29] YING R,YOU J X,MORRIS C,et al. Hierarchical graph representation learning with differentiable pooling[EB/OL]. [2020-04-30]. https://arxiv.org/abs/1806.08804.
[30] ZHANG X,CHEN L. Capsule graph neural network[EB/OL]. [2020-04-30]. https://openreview.net/forum?id=Byl8BnRcYm.
[31] SUTSLEVER I,MARTENS J,DAHL G E,et al. On the importance of initialization and momentum in deep learning[C]//International Conference on Machine Learning. New York,USA:ACM,2013:1139—1147.

