基于竞争粒子群算法的云计算资源调度策略

王镇道 张一鸣 石雪倩

摘    要：针对大规模云计算环境下的资源调度问题，提出了改进的竞争粒子群优化算法，以提高云计算资源调度效率. 基于多目标综合评价模型，首先建立包含任务完成时间、功耗以及负载均衡度的适应度函数，再利用混沌优化方法产生分布更加均匀的初始化粒子，引入自适应概率的高斯变异对胜利粒子位置进行更新，以提高种群多样性并增强全局搜索能力. 仿真试验表明，在相同的条件下，本文算法能够寻到最佳的调度方案，适用于大規模资源调度，且结果优于对比模型.

关键词：云计算;资源调度;负载均衡;竞争粒子群;混沌初始化;高斯变异;资源分配;算法

中图分类号：TP301                                文献标志码：A

Cloud Computing Resource Scheduling Strategy Based

on Competitive Particle Swarm Algorithm

WANG Zhendao1，ZHANG Yiming1?，SHI Xueqian2

（1. School of Physice and Electronics，Hunan University，Changsha 410082，China;

2. Nova Energie Co，Ltd，Changsha 410205，China）

Abstract：To solve the resource scheduling problem in the large-scale cloud computing environment， this paper proposes an improved competitive particle swarm optimization algorithm （ICSO） to improve the efficiency of resource scheduling in cloud computing. Based on the multi-objective comprehensive evaluation model， firstly， the fitness function including task completion time， power consumption and load balance are established. Then， the more evenly distributed initialization particles are generated by the chaos optimization method， and the Gaussian mutation of adaptive probability is introduced to update the position of the victory particles， so as to improve the population diversity and enhance the global search ability. Simulation results show that under the same conditions， the algorithm can find the best scheduling scheme， which is suitable for large-scale resource scheduling， and the results are better than the comparison model.

Key words：cloud computing;resource scheduling;load balancing;Competitive Particle Swarm Optimization algorithm（CSO）;chaos initialization;Gaussian variation;resource allocation;algorithms

云计算（Cloud Computing）是继分布式计算（Distributed Computing）、并行处理（Parallel Computing）、网格计算（Grid Computing）等之后计算模式的最新发展[1]. 云计算通过将各种互联的计算、存储、数据、应用等资源进行有效整合来实现多层次的虚拟化与抽象，用户只需要连接上网络即可方便使用云计算强大的计算和存储能力. 虚拟化技术是云计算中的关键技术之一[2]. 通过虚拟化技术，单个服务器可以支持多个虚拟机运行多个操作系统和应用，从而大大提高服务器的利用率，通过虚拟化为应用提供了灵活多变、可扩展的平台服务，用户租赁满足其需求的资源，并动态运行广泛的应用程序，由此可以看出云计算的核心问题是资源管理[3]. 考虑到云计算环境的动态性、海量数据、异构性、任务规模大等问题，云计算分布式系统上的资源调度是 NP-hard 问题. 对于求解计算时间长、复杂度高的问题，求解的算法主要有群智能优化算法. 例如模拟退火算法、遗传算法、粒子群优化算法、蛙跳算法等[4-7]运用在资源调度问题中取得了较好的效果，由于群智能算法在解决调度问题上的优异表现，因此被日益重视，但这些算法普遍存在对参数依赖度高、寻优效果不理想或者稳定性差等问题，且当优化问题存在大量局部最优解或为高维时，容易出现过早收敛. 这就导致随着云计算调度任务规模的越来越大，这些算法在大规模任务调度问题上整体性能下降，极易陷入“维数灾难”.

竞争粒子群算法（Competitive Particle Swarm Optimization，CSO）[8]通过引入成对的竞争机制实现粒子更新，不仅实现简单，而其在解决高维问题方面性能优越，已经被应用于解决大规模优化问题. 文献[9]提出利用竞争粒子群算法进行电网调度，表现出了优于同类算法的性能;文献[10]提出将二进制编码与竞争粒子群算法结合来解决电动车充电桩的需求管理问题，改进后的算法展现了在解决大规模、负載电力系统调度问题方面的优越性能;文献[11]通过对竞争粒子群优化算法的学习过程进行简化，然后将其应用于解决燃料电池模型的参数辨识问题，结果证明该算法在精度、鲁棒性、收敛性方面有很强竞争力.

本文在云计算资源调度中采用改进的竞争粒子群算法（Improved Competitive Particle Swarm Optimization，ICSO）对资源进行有效分配. 首先通过对任务完成时间、系统负载均衡度、任务完成功耗建立约束函数以兼顾三个目标的优化. 其次，在初始化操作中引入混沌映射，以改进收敛速度和寻优效率;引入自适应高斯变异操作对胜利粒子位置进行更新以提高算法搜索精度. 仿真结果表明，本文算法在任务完成时间、任务执行功耗以及系统的负载均衡之间取得较好的平衡，提高了在大规模任务下的云计算资源的利用率.

1   云计算任务调度

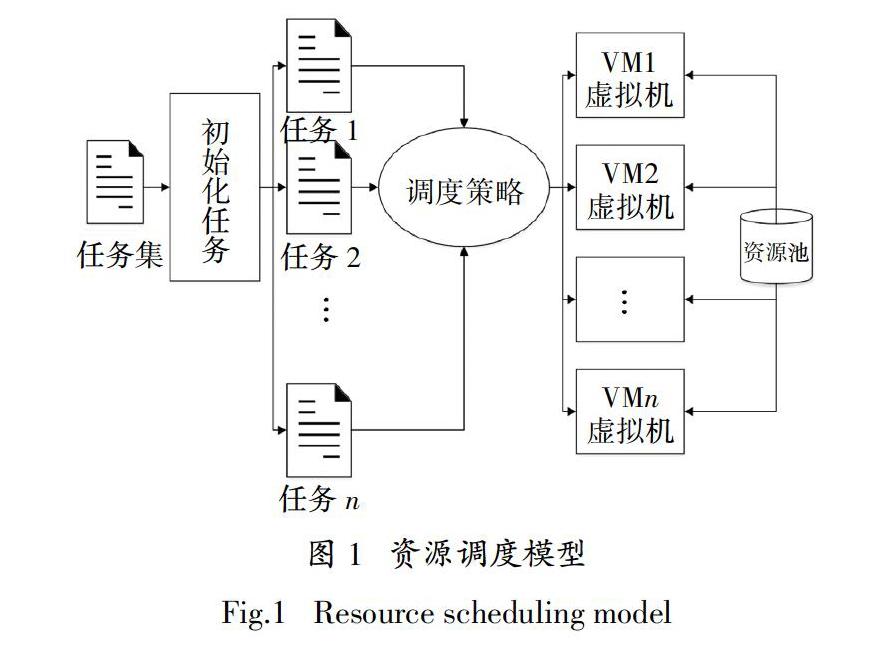
当前云计算系统主要采用Map/Reduce架构模式，通过对用户任务进行分配来完成任务调度. 具体来说，任务调度是指在云计算环境中根据任务和资源的实际情况，将任务分配或迁移到相应资源上执行的过程[12]，图1为云计算平台中任务调度的一般过程.  任务调度涉及了优先权、执行时间、完成时间、资源利用率、成本、能耗、网络吞吐率以及公平性等优化参数和测评指标[13]. 任务调度策略不仅直接对任务执行时间和成本产生作用，还会影响到整个云计算平台的性能.

1.1   云计算任务调度数学模型

在云计算资源环境中，设资源节点共有n个，用集合v = {v1，v2，v3，v4，…，vn} 表示，其中vj（1 ≤ j ≤ n）表示第j个虚拟资源节点，将任务划分成m个子任务，子任务表示为T = {t1，t2，t3，t4，…，tm}，其中第i个任务表示为ti（1 ≤ i ≤ m）. 每个子任务分配到一个虚拟资源节点运行，子任务分配到虚拟资源节点的情况可以用矩阵P表示为：

P = p11    p12    …    p1m

p21    p22    …    p2m

[…]    […]            […]

pn1    pn2    …    pnm       （1）

式中：元素pji代表一个子任务ti和虚拟资源节点vj的对应关系. 当子任务ti分配到vj时，pji = 1，反之为0，即pji∈{0，1}. 每个任务只能分配到某一个虚拟资源节点上执行，所以有：

pji = 1，1 ≤ i ≤ m         （2）

考虑到云计算平台资源的异构性，即不同的虚拟节点所具有的能力侧重点不同，有些节点资源的运算能力较强而带宽较小，而有些节点资源的内存较大而计算能力较弱等. 基于以上特性，可以用（VC，VM，VB）表示虚拟机节点的资源能力，其中 VC 表示 CPU 的运算能力（每秒处理百万级指令的能力），VM 表示内存的大小，VB表示带宽大小，而子任务对处理节点的需求采用P（Ci，Mi，Bi）描述，表示执行任务Pi需要的CPU 处理能力、内存及网络带宽.

1.2   服务质量模型

服务质量是用来衡量云计算资源调度中任务的完成程度的指标. 由于云计算的任务调度是一个多目标优化问题，综合评价云计算任务调度的优良需要从多方面进行考虑，根据前面对任务调度性能指标的描述. 首先给出3个优化目标：任务完成总用时Tmax、任务完成功耗E、负载均衡度Bdegree.

对于虚拟机节点在处理任务时，它的单个任务耗时可以表示为：

Tji =             （3）

式中：Li表示完成第i个任务的长度;VC j为第j个虚拟节点的CPU处理能力. 第j个虚拟节点处理任务总耗时为：

Tj = Tji            （4）

则任务总用时Tmax为各虚拟机节点完成时间中的最大值，即

Tmax = max（pji Tji），1 ≤ j ≤ n         （5）

按照目前的研究表明，单位时间能耗和CPU利用率是线性关系的[13]，结合能耗的计算公式E = P × T，任务从t0时刻到t1时刻所产生能耗可以表示为：

E（M） = Pdt         （6）

系统完成任务的总功耗为各节点功耗总和：

E = E（M）i = kVOC j tji         （7）

式中：VOC j为虚拟机节点j的CPU利用率;tji为虚拟机节点j执行任务耗时;k为乘法算子. CPU利用率计算方法为：

VOC j =  × 100%         （8）

式中：ci、vci分别表示任务对CPU处理能力的需求以及虚拟机节点所能提供的CPU运算能力. 同理虚拟机资源j中内存的利用率和带宽利用率可以分别表示为：

VOM j =  × 100%         （9）

VOB j =  × 100%         （10）

在云计算执行任务过程中，虚拟机的负载主要是由其执行的任务量的大小和自身的计算能力所决定，虚拟机Vj负载情况表示为Vj = {Mj，Cj，Bj}，其中Mj、Cj、Bj分别表示虚拟机Vj上的内存利用率、CPU利用率和带宽利用率. 则虚拟机资源j的利用率为：

VO j = k1

+k2

+k3

×100%

（11）

k1 + k2 + k3 = 1          （12）

式中：k1、k2、k3分别为CPU、内存、带宽的权值. 整个系统的虚拟机资源平均利用率为：

Vavg =  × 100%         （13）

以各个虚拟机节点利用率之间的标准差系数作为表示集合v = {v1，v2，v3，v4，…，vn}中虚拟机负载情况，则系统的负载均衡度Bdegree可以表示为：

Bdegree =          （14）

2   任务调度策略

2.1   竞争粒子群算法

粒子群优化算法（Particle Swarm Optimization，PSO）作为最经典的群智能算法之一，由于其简单的实现和快速的收敛性，被广泛应用于求解单目标优化问题（Single-Objective Optimization Problem，SOP）. 然而，当优化问题存在大量的局部最优解或为高维时，PSO算法性能较差. 竞争群优化算法是粒子群优化算法的一個变体，Cheng和Jin[8]提出的 CSO算法模拟了生物学中的优胜劣汰的个体竞争机制. 采用竞争机制的优化算法比原粒子群优化算法能够更好地平衡收敛性和多样性. 而且在大规模优化问题上，该算法表现出良好的性能和可拓展性. 该算法假设种群大小为 M，在解空间内随机地初始化种群. 在每一次迭代过程中首先将种群随机均分为2组，两组粒子两两进行竞争比较，根据适应值的大小分别为胜利者（Winner）与失败者（Loser），胜利者将直接进入下一代，失败者根据式 （15）和式 （16） 向胜利者学习并更新自身位置和速度.

vL（t + 1） = r1（t） × vL + r2（xw（t） - xL（t）） +

φr3（x（t） -  xL（t））              （15）

xL（t + 1） = xL（t） + vL（t + 1）          （16）

式中：xw（t）、xL（t）分别表示胜利者和失败者的位置向量;vL（t + 1）表示失败者的速度向量;t为迭代次数;r1（t）、r2（t）、r3（t）∈[0，1]D是3个服从均匀分布的随机向量，与解向量有相同的维数;φ是一个参数，用于控制x（t）对失败者位置更新的影响;x（t）有两种含义，一种表示所有粒子的平均位置，具有全局性;另外一种表示领域内粒子的局部平均位置，具有局部性. 在本文中x（t）使用全局平均位置.

2.2   改进的竞争粒子群算法

标准的CSO算法具有操作简单，所需参数较少，易于实现等优点，但由于CSO算法在每次迭代过程中只更新失败粒子的位置和速度信息，这使得种群多样性不足，最终导致算法陷入局部最优解及“早熟”现象. 因此，为了增强种群的多样性，平衡种群的探索与开发，本文借鉴遗传算法中的变异思想，在CSO算法中引入自适应高斯变异，用来对胜利粒子的位置进行更新，同时引入混沌初始化策略对初始种群进行初始化.

2.2.1   混沌初始化策略

在标准CSO算法中，种群的初始化是随机产生的，初始位置的散布程度及其在搜索空间中的位置是否均匀，将直接影响整个搜索过程的收敛速度和算法的寻优效率[14-15]. 混沌是一种无规则的运动状态，具有非常强烈的非线性特点，它有规律性、随机性和遍历性等特点，其基本思想是根据一定规则把变量从混沌空间映射到求解空间. 本文利用混沌优化策略对粒子群进行初始化，Logistic映射具有较均匀的遍历性分布区间，能产生分布均匀的混沌序列，有效地保证了种群在解空间中的均匀分布，从而提高算法的搜索效率. 本文选取Logistic映射的方法产生初始混沌序列. 该映射的表达式为：

xn+1 = μxn（1 - xn）              （17）

式中：xn为混沌变量;参数μ∈（0，4];n为混沌变量序号，n=1，2，3，…，m. 映射图像如图2所示，当3.569 9 < μ≤4时，系统处于混沌状态，在本文中μ取值为4.

本文利用混沌迭代生成初始化粒子群位置，具体步骤如下：

1）对于D维空间中的n个初始粒子位置，首先随机产生一个D维向量作为第一个混沌向量，即r1∈[0，1]D;

2）将r1的每一维利用式（17）进行n-1次迭代，生成n-1个混沌向量，r2、r3、…、rn;

3）将产生的n个混沌向量按照式（18）映射到解的搜索空间.

xi = xmin + （1 + ri）            （18）

式中：xmin、xmax分别为搜索空间的上下限;xi即为第i个混沌初始化粒子位置信息.

2.2.2   自适应高斯变异

由于变异算子在提升算法收敛性能和种群多样性方面有着显著表现，文献[16]将高斯变异引入到PSO算法中以改善粒子在求解过程中的多样性，提出一种基于高斯变异的多目标粒子群优化算法. 本文将高斯变异引入CSO算法中对胜利粒子的位置进行更新，变异操作如下：

xt+1 = xt + c × γ，rand（0，1） ≤ Pm

xt+1 = xt，rand（0，1） > Pm      （19）

式中：c为变异步长;γ为服从高斯分布Gauss（0，1） 的随机变量;Pm为变异概率. 同时考虑到迭代初期主要发挥竞争群算法自身的特点，采用较小的变异率，随着迭代进行，种群多样性逐渐降低，相应地增加了种群的变异概率，因此将变异概率设定为随迭代次数线性递增，使变异概率自适应变化. Pm的计算公式为：

Pm = Pm，min +      （20）

式中：Pm，min为最小变异率;Pm，max为最大变异率;k为当前迭代次数;N为最大迭代次数. 从更新公式可见，随着迭代次数的增加，变异概率线性递增. 因此，引入自适应高斯变异后胜利者的更新如式（21）所示.

xw（t + 1） = xw（t） + δ × Gauss（0，1） ×

xw（t） - [x]（t），rand（0，1） ≤ Pm

xw（t + 1） = xw（t），rand（0，1） > Pm    （21）

式中：δ为乘法算子;[x]（t）为所有粒子的平均位置，以胜利粒子的当前位置和全局粒子的平均位置的差值作为变异步长;rand（0，1） 为服从[0，1]均匀分布的随机数.

3   基于ICSO的云资源调度算法设计

3.1   粒子编码与适应度函数设计

设任务数m，虚拟资源节点数 n，本研究中每一个粒子代表一种任务分配方案，假设粒子所表示的解向量P = { p1，p2，…，pn}，N 表示向量 P 的维数，Ni 表示向量 P 第 j 维的值，则 Nj = i 表示任务 j 分配到虚拟机 i.

由于本文涉及到多个目标的优化过程，适应度函数与任务完成总用时Tmax、任务完成功耗E、负载均衡度Bdegree 3个目标相关联，所以首先需要将多目标问题转化为单目标问题. 首先将各个优化目标参数归一化，如式（22）所示：

F =         （22）

式中：F代表归一化后的值;f（x）表示当前系统中某一个优化目标参数大小;f（x）max、 f（x）min分别表示该目标参数的最大值和最小值. 通过对单个优化目标适应度值加权，将多目标优化问题转化为单目标优化问题. 适应度函数可以表示为：

fi = w1FT + w2FE + w3FB        （23）

式中：fi表示第i个粒子的适应度值;w1、w2、w3分别表示任务完成总用时Tmax、任务完成功耗E、负载均衡度Bdegree 3个目标对应的权值，且 w1+w2+w3=1.

3.2   改进竞争粒子群算法的任务调度

将本文提出的ICSO算法应用于云计算资源调度问题中，调度算法的具体实现步骤为：

步骤1   将云计算任务调度方案与ICSO算法中的粒子位置进行一一对应，粒子的最佳位置即为最佳任务调度方案;

步骤2   初始化参数. 给出任务集数据、虚拟机参数，算法的最大迭代次数Maxcycle、种群规模m、变异步长;

步骤3   按照公式（17）（18）对粒子群初始位置进行混沌初始化;

步骤4   根據式（23）计算每个粒子的适应度值;

步骤5   将种群随机进行两两竞争比较，根据适应度值的大小分为胜利者Winner和失败者Loser;

步骤6   根据式 （15）（16），更新失败粒子速度以及位置，根据式 （19）更新胜利粒子的位置和速度. 计算更新粒子的适应度值并更新全局最优值和最优解;

步骤7   达到最大迭代次数的时候，算法结束，转到步骤8，否则继续步骤5;

步骤8   得到最优粒子位置，即得到最优的任务调度方案.

4   试验测试和结果分析

本文采用CloudSim模拟云计算平台的仿真环境对算法进行验证[17-18]，具体的试验环境为：Window10操作系统，IntelCoreTM i5-8250U，1.60 GHz CPU，16.00 GB内存，CloudSim 4.0. 将本文提出的改进的竞争群算法ICSO与文献[13]中的竞争群算法以及基本PSO算法和GA算法进行了比较. 各算法试验参数设置如表1所示.

试验中考虑了资源的处理速度和待处理任务的长度，设定两个任务集T1、T2，分别设置任务数量为10～100和1 000～5 000，代表小规模和大规模两种任务规模情况. 计算节点数为10，随机设置虚拟节点的性能，设置虚拟节点能力为 [1 000，2 000] mi/s，内存为 [512，2 048] MB，带宽为[5 000，10 000] bit/s，在[500，9 000]间随机设置任务长度，最大迭代次数为200次，为排除偶然性，每种方法进行10次独立重复试验，并取平均值作为最终的试验结果.

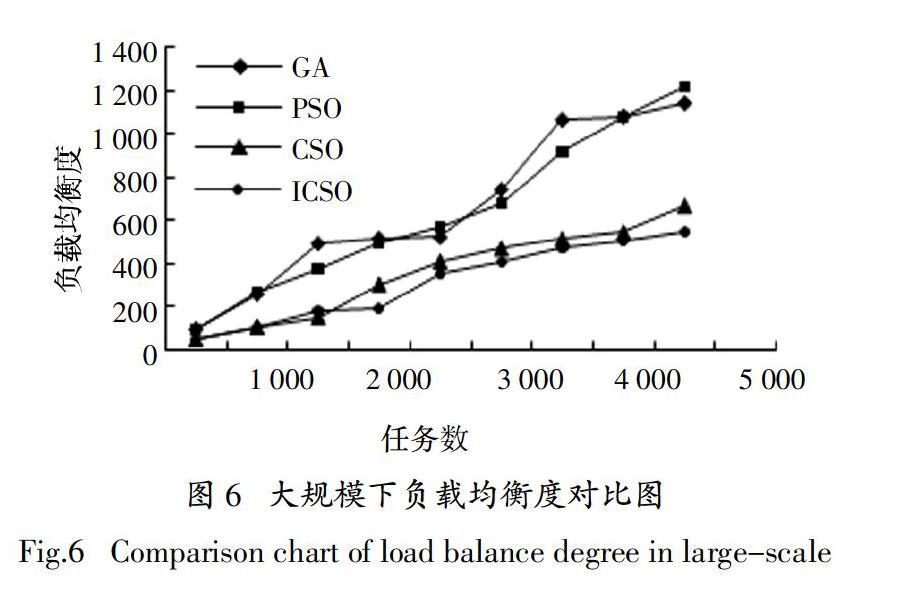
为了验证本文所提调度模型和算法的有效性，通过改变迭代次数、任务数来比较改进算法和对比算法在各个维度的差别. 首先，分别在大规模和小规模两个任务集中保证迭代次数相同的条件下 ，在任务完成时间、功耗、负载均衡度3方面做出对比. 试验结果如图3～图8所示.

1）图3和图4分别为ICSO算法、CSO算法、GA算法和PSO算法在小规模和大规模任务数量下的任务完成时间结果对比图. 可以看出，当任务数量较少时，ICSO算法与试验对比算法任务完成时间相差不大. 随着任务数量的增多，CSO和ICSO算法在大规模任务下具有明显的优势，ICSO和CSO算法的任务完成时间明显优于PSO和GA算法，ICSO算法的任务完成时间又优于基本的CSO算法，说明本文改进的ICSO算法在减少任务完成时间方面有所提升.

2）图5和图6分别为2种任务集下4种算法的负载均衡度对比图. 随着任务数量的增多，4种算法的任务调度策略的负载均衡度都在上升，但ICSO和CSO算法任务调度策略下负载均衡度上升速率明显小于PSO调度策略和GA调度策略;在整个过程中，ICSO调度算法下的负载均衡度始终低于另外2种算法. 这主要是因为ICSO算法中引入的变异算子提升了种群的多样性，很好地避免了局部最优，使得最后的结果更好.

3）图7和图8为2种任务集下的4种调度策略的任务完成功耗对比图. 从图中可以看出，在任务数量较少时，ICSO、CSO算法和PSO算法以及GA算法完成的云计算资源调度在任务完成功耗上差别不大，但随着任务数量的增多，CSO和ICSO算法在大规模任务下的优越性得到了体现，PSO算法下的调度策略功耗明显高于CSO和ICSO算法下的调度策略，而ICSO算法的功耗又略低于CSO算法的功耗，这说明改进的算法在降低任务完成功耗方面也有所提升.

从迭代次数的角度进行对比，将任务数设置为3 000，比较迭代次数对最优适应度值的影响. 结果如图9所示.

由图9可知，在初始阶段CSO算法和改进的ICSO算法收敛速度要高于PSO算法和GA算法，在迭代40次前，各算法所得适应度值差别并不明显，这时CSO算法略优于其他3种对比算法;随着迭代次数增至60以上，CSO算法和ICSO算法所求结果明显好于PSO算法和GA算法，且两种算法在80次开始逐渐趋于稳定，而PSO算法在120次以后才开始趋于稳定. 在收敛速度方面，CSO算法略微好于ICSO算法，这主要是由于引入的变异操作在一定程度上降低了算法的收敛速度;从求解精度上可以看到，ICSO算法能够跳出局部最优解，实现更好的求解精度，算法结果表现更加优秀.

5   结   论

针对大规模云计算资源调度中算法求解精度不高，易陷入局部最优等问题，本文提出改进的竞争粒子群优化算法来求解云计算资源调度问题. 相较于标准的竞争粒子群算法，该算法利用混沌理论产生初始化种群，使得初始化粒子在解空间中均匀分布;在粒子搜索过程中引入自适应变异概率的高斯变异来进行胜利粒子的更新，提升了种群多样性和算法的全局搜索能力. 在CloudSim仿真环境下，分别從不同任务规模下的求解精度与相同任务规模下的收敛速度两方面进行试验. 仿真结果表明，本文提出的多目标综合评价模型兼顾了云计算任务的完成时间、功耗以及负载均衡度，能搜索到最佳调度方案，可很好地应用于大规模云计算环境下的资源调度问题.

参考文献

[1]    THAIN D，TANNENBAUM T，LIVNY M. Distributed computing in practice：the Condor experience[J]. Concurrency and Computation：Practice and Experience，2005，17（2/3/4）：323—356.

[2]    MISHRA B，PANDEY D R. Different approaches of virtualization in cloud computing[J]. International Journal of Scientific Research，2017，5（11）：221—227.

[3]    TOPCUOGLU H，HARIRI S，WU M Y. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Transactions on Parallel and Distributed Systems，2002，13（3）：260—274.

[4]    ABDULLAH M，OTHMAN M. Simulated annealing approach to cost-based multi-QoS job scheduling in cloud computing enviroment[J]. American Journal of Applied Sciences，2014，11（6）：872—877.

[5]    SAFWAT A，FATMA A. Genetic-based task scheduling algorithm in cloud computing environment[J]. International Journal of Advanced Computer Science and Applications，2016，7（4）：550—556.

[6]    胡志剛，常健，周舟. 面向云环境中任务负载的粒子群优化调度策略[J]. 湖南大学学报（自然科学版），2019，46（8）：117—123.

HU Z G，CHANG J，ZHOU Z. PSO scheduling strategy for task load in cloud computing[J]. Journal of Hunan University（Natural Sciences），2019，46（8）：117—123. （In Chinese）

[7]    DENG Y，CHENG X H. A heterogeneous multiprocessor task scheduling algorithm based on SFLA[C]//World Automation Congress. Guilin：IEEE，2016：1—5.

[8]    CHENG R，JIN Y C. A competitive swarm optimizer for large scale optimization[J]. IEEE Transactions on Cybernetics，2015，45（2）：191—204.

[9]    WANG Y，YANG Z L，GUO Y J，et al. A novel binary competitive swarm optimizer for power system unit commitment[J]. Applied Sciences，2019，9（9）：1776.

[10]  WANG Y，YANG Z L，MOURSHED M，et al. Demand side management of plug-in electric vehicles and coordinated unit commitment：a novel parallel competitive swarm optimization method[J]. Energy Conversion and Management，2019，196：935—949.

[11]  XIONG G J，ZHANG J，SHI D Y，et al. A simplified competitive swarm optimizer for parameter identification of solid oxide fuel cells[J]. Energy Conversion and Management，2020，203：112—114.

[12]  马小晋，饶国宾，许华虎. 云计算中任务调度研究的调查[J]. 计算机科学，2019，46（3）：1—8.

MA X J，RAO G B，XU H H. Research on task scheduling in cloud computing[J]. Computer Science，2019，46（3）：1—8. （In Chinese）

[13]  AKHTER N，OTHMAN M. Energy aware resource allocation of cloud data center：review and open issues[J]. Cluster Computing，2016，19（3）：1163—1182.

[14]  程泽，董梦男，杨添剀，等. 基于自适应混沌粒子群算法的光伏电池模型参数辨识[J]. 电工技术学报，2014，29（9）：245—252.

CHENG Z，DONG M N，YANG T K，et al. Extraction of solar cell model parameters based on self-adaptive chaos particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society，2014，29（9）：245—252. （In Chinese）

[15]  TAN W A，ZHAO Y. Web service composition based on chaos genetic algorithm[J]. Computer Integrated Manufacturing Systems，2018，24（7）：1822—1829.

[16]  HU M，WU T，WEIR J D. An adaptive particle swarm optimization with multiple adaptive methods[J]. IEEE Transactions on Evolutionary Computation，2013，17 （5）：705—720.

[17]  CALHEIROS R N，RANJAN R，BELOGLAZOV A，et al. CloudSim：a toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms[J]. Software：Practice and Experience，2011，41（1）：23—50.

[18]  XU B，PENG Z P，XIAO F X，et al. Dynamic deployment of virtual machines in cloud computing using multi-objective optimization[J]. Soft Computing，2015，19（8）：2265—2273.