排队论模型在医院分诊系统中的应用

姚 颖

（辽宁师范大学，辽宁大连 116000）

基于排队论分析，在不影响患者就诊质量的情况下，通过建立数学模型压缩排队就诊的时间[1]。本文选取大连某医院为研究对象，根据实际数据建立排队模型。通过分析诊室排队系统，在各个环节缩短患者的等待时间、提高就诊效率、满足患者的需求、减少资源浪费、改善服务质量、降低门诊服务成本、提高医院效益。

1 医院分诊系统排队模型

1.1 医院分诊排队系统分析

（1）输入过程。

不同类型的患者按照不同规则输入，总数有限或无穷、单独或分批到达、连续到达间隔确定或随机、患者的输入独立或相关、输入过程稳定或不稳定。

（2）排队规则。

患者到达诊室挂号等待，代表进入排队系统，排队依次进入诊室，诊断完成离开诊室即离开排队系统。

1.2 医院分诊系统模型

（1）M/M/1/K排队模型。

假设系统的空间为K，患者X1到达诊台1接受医疗诊断，之后患者2进入排队系统，进行同样流程操作，直到患者XK的位置无空闲时，新到患者自动离开，反之则进入系统排队等待，如图1所示。

图1 单队单服务台模型

基于M/M/1/K排队模型，排队系统的平衡方程为：

由文献[2]可知：

患者损失率：

系统空闲率：

当ρ≠1时，平均队长为：

当ρ=1时，平均队长为：

平均排队长：

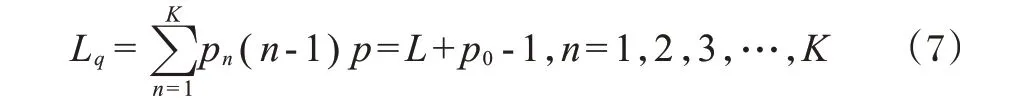
患者的到达率设为λ，针对排队系统内的K-1个排队位置，系统无空闲时患者无法进入，故可进入系统的实际概率为1-pK，即单位时间有效到达率为：

式中：pk——患者损失率。

平均逗留时间：

平均等待时间：

（2）M/M/S/K排队模型。

假设系统的空间为K，设诊台数量为S，患者X1到达诊台1接受医疗诊断，之后患者2进入排队系统，进行同样流程操作，直到患者XK的位置无空闲时，患者按照优先权形成XK、YK、ZK等多个队列前往到最多S个诊台，如图2所示。

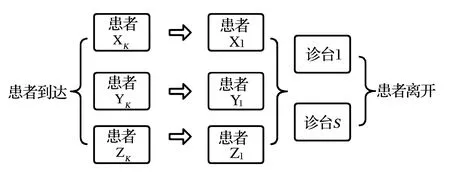
图2 多队多服务台模型

假设某天某门诊安排坐诊医生m人，患者到达诊台接受医疗诊断，相继到达时间服从参数为λ的负指数分布，后到达的患者进入排队系统，进行同样流程操作，假设系统空间K是无限的，直到最后有一个位置无空闲时，即当前诊台就诊患者数满时，患者按照不同的优先权形成多个队列去往其他诊台挂号就诊。此情况为典型M/M/S/K多服务台混合制排队模型，求得该条件下的定量指标。

1.3 医院效益分析理论

（1）最优服务人数。

在排队系统中，诊台数量决定服务质量和效率，但医院不能盲目投入人员和设备，应优化服务成本。

式中：Z——单位时间服务成本与患者逗留费用之和的期望值；Cs——单位时间诊台成本；Cw——单位时间的单个患者停留费用；M——最优服务人数。

（2）最优服务率。

当μ=1时，最优服务率z：

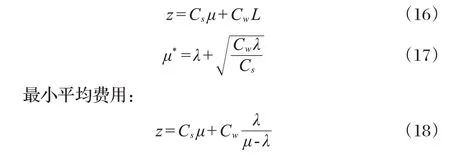
2 实证分析

2.1 数据来源

大连某医院有多个门诊，挂号所需平均时间相同，根据数据模拟某工作日门诊具体排队情况，如表1所示。

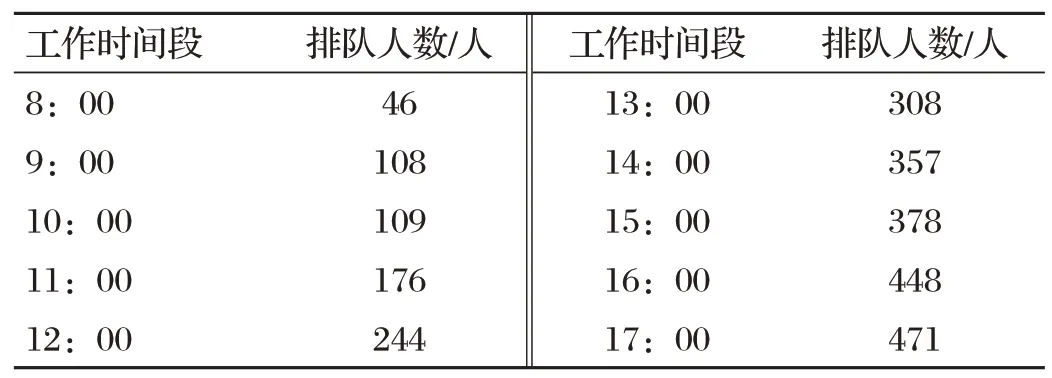
表1 某工作日患者就诊排队情况模拟

2.2 分析过程

（1）泊松分布证明过程。

设N(t)表示(0,]t时间内抵达医院的患者数量，采用卡方检验法，检验患者到达医院门诊的排队输入过程是否符合泊松分布的条件：

选取样本容量，假设输入过程患者数为200人，根据模拟某工作日患者就诊排队数据观察结果如表2所示。

表2 某工作日患者就诊排队频数统计

点估计λ=2.49，取显著水平α=0.05，根据相关信息查表得出在水平0.05下可接受假设H0，即认为患者为泊松流。

（2）M/M/1/K排队模型分析过程。

运用M/M/1/K排队模型进行分析，假设某天某位医生的门诊实际就诊患者数为30人，平均每分钟可服务一个患者；每两分钟会有一位患者进入排队系统，直到最后一个位置无空闲时，新到患者自动离开；根据排队模型分析过程计算相关数据，p30=0.03、L=15、Lq=14.03、W=11.07、Wq=10.35。

（3）M/M/S/K排队模型分析过程。

运用M/M/S/K排队模型进行分析，假设某天某门诊安排两名医生，每位医生每天限挂号30人，假设每位医生的平均服务时间为6 min，当某一位医生号满时，患者通常会选择其他的医生挂号就诊。假设每分钟有2名患者到达门诊，则某诊台空闲概率p0为1.45×10-19。由于患者数量远大于医生数量，从到达率的角度可以认为排队系统没有空闲时间。根据排队模型计算相关数据，p30=0.75、L=23.75、Lq=26.75、W=47.5、Wq=41.5。

（4）费用损失率分析过程。

顾客平均到达率和平均服务率如表3所示。

表3 服务人数与队长

由L(M)-L(M+1)≤Cs/Cw≤L(M-1)-L(M)可得M=7，安排7个医生，诊断效率增加一倍，理想情况下该科室的利润P=7×Cw×μ×（α-e）-（CsM+E）=13 366.93元。

假设某天某门诊只安排3个医生坐诊，导致排队拥堵或人员流失的现象，医院损失费用F=7×Cw×(λ-μs)×(α-e)，代入数据得3 047.74元，费用损失率为22.8%。

综上，排队论的应用对于医院提升服务效率和服务水平具有重要作用。

3 结语

本文引入排队模型，建立排队系统，通过分析医院相关数据得出结论。通过将有关的排队论模型引入医院实际排队系统当中，可以为医院把握成本和就诊质量提供一定理论基础。