航空发动机叶轮机流场数值模拟方法研究
唐晓毅 余雅琪
(中国航发湖南动力机械研究所,湖南株洲 412002)
随着航空发动机朝着高性能方向发展,对叶轮机设计提出了更高的要求,因而采用CFD技术结合优化设计方法成为重要的设计手段。由于优化设计方法需要计算大量样本以进行寻优或建立代理模型[1-3],CFD求解器的计算时间成为设计时间成本中的主要部分。计算准确度高、收敛速度快、鲁棒性好的CFD求解器可极大的缩短设计周期,节约成本。Jameson等人提出的JST格式在全三维数值仿真中得到广泛应用,该格式采用一阶后差格式离散N-S方程时间项,中心差分离散N-S方程空间项,加入人工粘性保证计算的稳定性。该格式为二阶精度,计算量较小、收敛速度快、鲁棒性好,自格式推出后不断得到改进,在叶轮机械CFD领域得到了广泛的应用。
本文基于改进的JST格式[4-6],自主开发了叶轮机数值模拟求解器,为满足高精度流场快速仿真需求,对Spalart-Allamaras湍流模型方程及滑移壁面函数的应用进行研究,开展了高负荷压气机转子叶片流场模拟,通过与试验流场、数据对比,验证了计算方法的正确性。
1.N-S方程求解
本文求解器采用有限体积法求解N-S方程,坐标系其绝对圆柱坐标系(z,θ,r)。其中,考虑转速的积分形式守恒型N-S方程为:
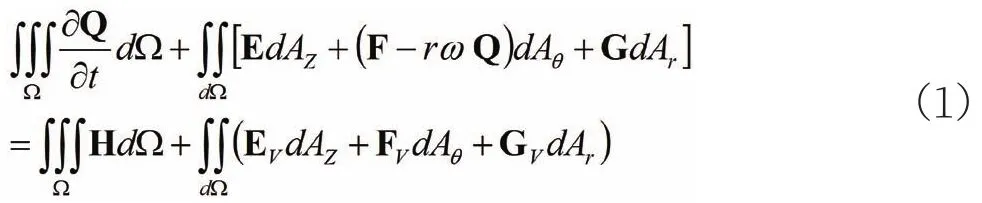
其中Ω为网格单元控制体,Az,Aθ,Ar分别为控制体表面在相应坐标轴方向的投影面积。守恒变量矢量为Q,ω为旋转角速度。矢量(E、F和G)、(Ev、Fv和Gv),对应(z,θ,r)方向的对流通量及粘性通量,源项为H。采用基于JST格式的五步混合Rung-Kutta显示时间推进法求解方程,应用了当地时间步长、隐式残差光顺技术加速收敛[5]。
2.Spalart-Allamaras湍流模型方程
S-A模型由Spalart和Allamaras[6-7]于1992年提出,通过求解中间变量的控制方程计算湍流粘性系数,方程的封闭系数经过丰富的实验数据调校,拥有较高的准确度,相对于零方程湍流模型(如B-L模型),S-A模型计算得到湍流粘性系数在整个流场内保持连续,对存在分离现象的流场也适用,对网格量要求低,方程收敛性好,本文采用S-A模型计算湍流粘性,在保证湍流粘性计算精度的同时获得较高的计算效率。
同N-S方程(1)式一致,本文在文献[6]中S-A方程通过引入连续方程,得到了积分形式的守恒型S-A模型方程:
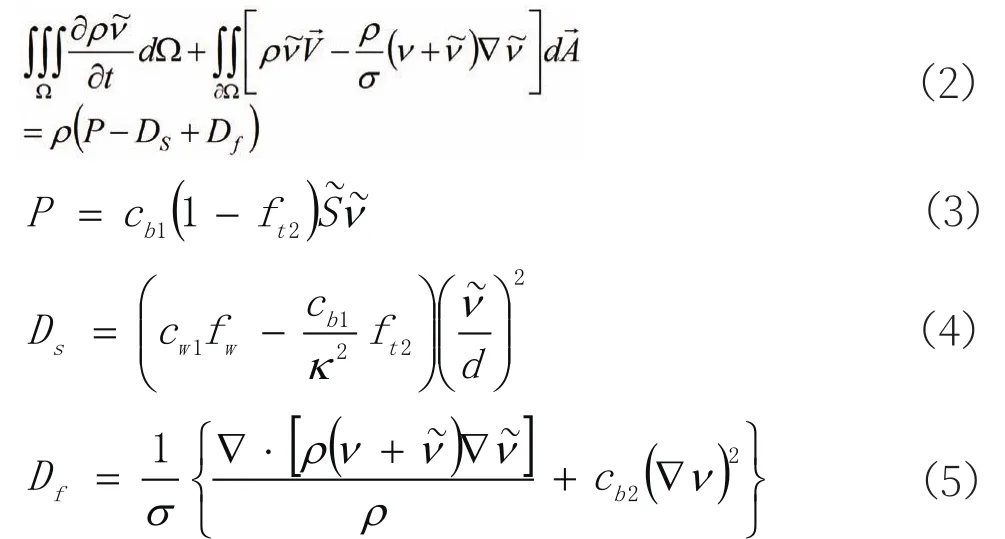
方程左端第二项分别代表湍流方程无粘通量和粘性通量,P、Ds和Df为方程源项表达式。由于引入了连续方程,Df有别于标准表达式,并且本文将其中的交叉偏导项作为粘性项消除了梯度计算的困难。
实际应用中,S-A方程偶尔存在计算发散的现象,综合分析发现主要原因为源项量值过大,因此对进行限制,防止其出现负值或小值:
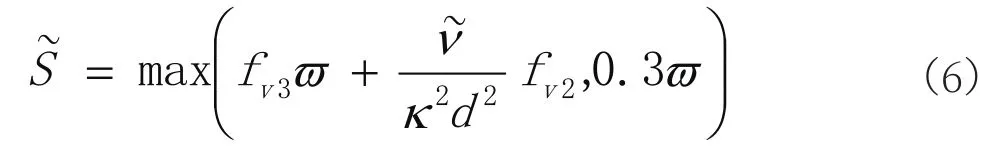
对r进行限制,防止其值过大:

壁面处给定为=0,在方程求解过程中限制µt≤5000µl。为增强S-A方程计算的稳定性,对源项(4)、(5)式采用相同格式进行了隐式处理,如(4)式处理方法为:
以增强计算不稳定工况点附近湍流方程求解的稳定性。变量定义及公式中常量见文献[6]中值。
3.壁面边界条件设置
对于无滑移壁面边界条件,如需准确模拟壁面附近粘性底层的流动,需在靠近壁面处布置大量网格,使壁面附近的无量纲距离Y+<10。为了减少近壁面处对网格量及网格尺寸的要求,本文利用Denton[8]提出的壁面函数对壁面附近粘性底层流动进行模拟,假设近壁面第一层网格处在层流底层或者湍流对数律区外,壁面处流体摩擦系数可通过式(9)求出:
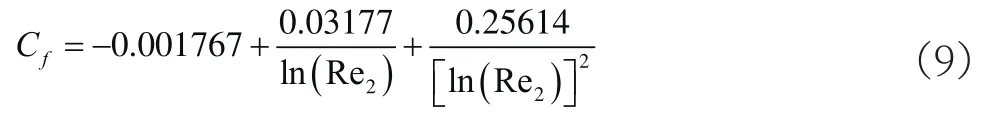
式(9)中Re2的参考长度为靠近壁面第一层网格的法向距离,参考速度为靠近壁面第一个网格点处的相对速度Vref。计算得到摩擦系数Cf之后,可计算出壁面处的切应力:

4.算例验证
NASA Rotor 37为压比20核心压气机的进口级转子,其基元叶型为多圆弧叶型,采用低展弦比、高稠度设计的,其叶片进口相对马赫数均为超声速,设计压比2.1,绝热效率高达0.877[9],其内部流场结构复杂,成为众多学者的研究对象。本文也以其为对象检验所开发求解器的准确性。
在经过网格无关性验证后,最终选定网格数为:119×39×45(流向×周向×展向),总体网格单元数约20万,图3为本文采用的Rotor 37的计算网格,在其叶顶间隙设置了3层网格,叶片通道内共55个网格点,在叶片前、后缘处加密网格以增强对前、后缘圆弧的模拟,如图1所示。经过约1300个时间步后连续方程残差相对值下降了4个数量级,进出口流量平衡,达到收敛标准,残差收敛史见图2。
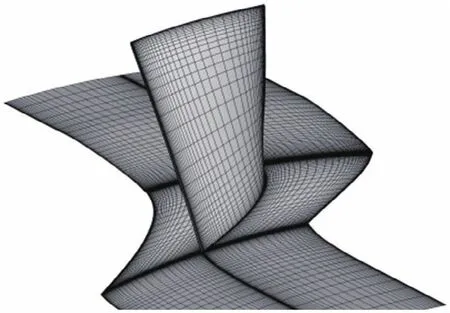
图1 NASA Rotor 37计算网格
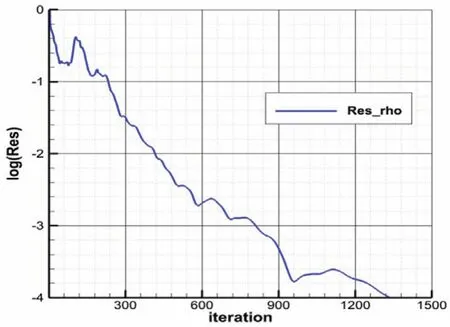
图2 连续方程残差收敛史
数值计算得到的特性曲线如图3、图4所示。从图中可以看出,特性曲线的变化趋势与试验值一致。在数值上,压比特性计算值略高于对应试验值,而效率特性预测值总体偏低,偏差约为2%,显示出较高的精度。表1给出了计算与试验性能参数对比,可见计算精度不低于3%。
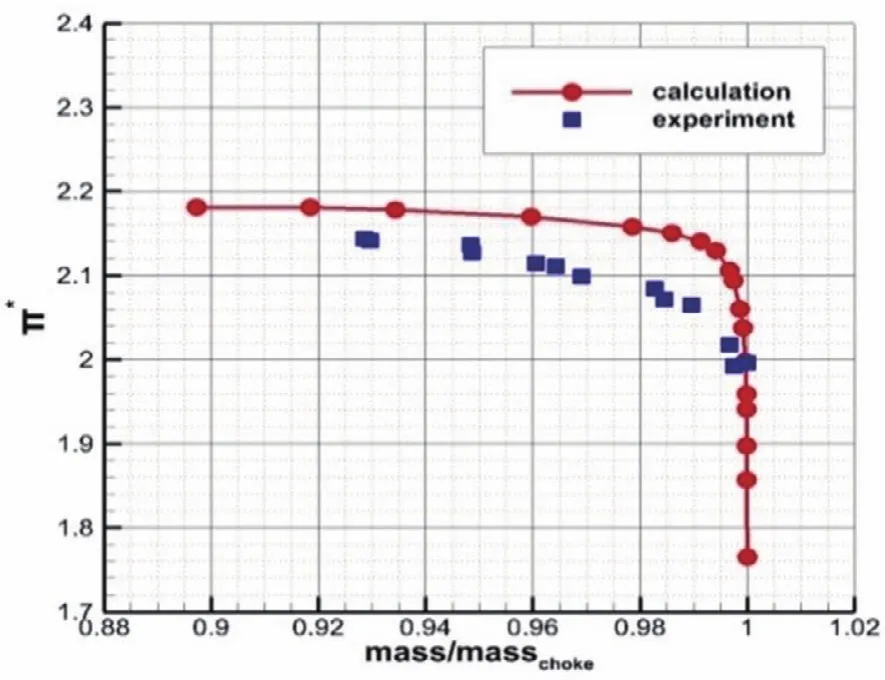
图3 NASA Rotor 37计算与试验压比特性曲线
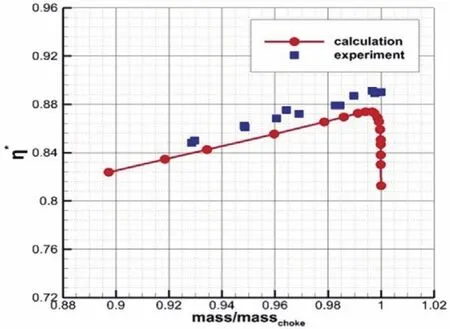
图4 NASA Rotor 37计算与试验效率特性曲线
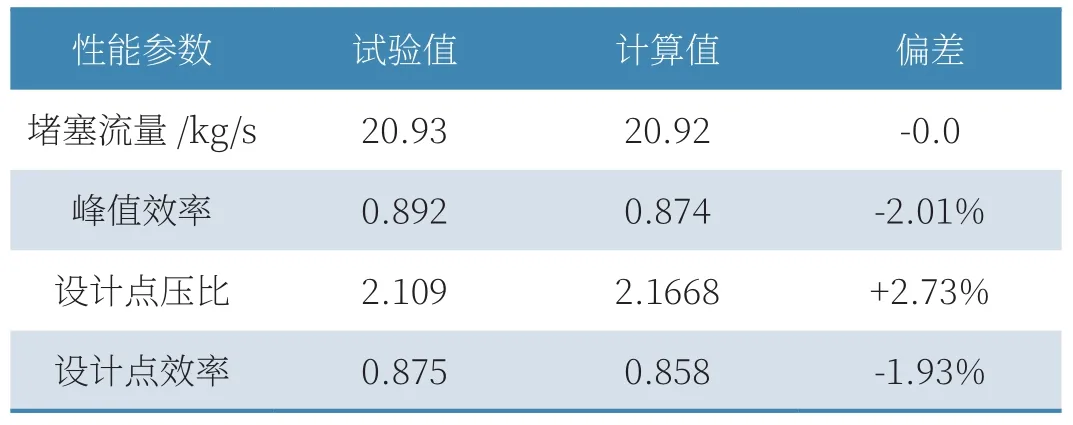
表1 NASA Rotor 37计算与试验性能参数对比
S-A湍流模型能够有效模拟存在分离的流动,并且能得出满意的湍流粘性分布和模拟尾迹,为验证所开发求解器对尾迹模拟的可靠性,图5为Rotor 37转子出口测量站50%叶高相对马赫数分布,由图中可以看出,计算结果在马赫数数值大小、尾迹大小和尾迹宽度等流动细节方面均与试验测量值一致,进一步表明了本文所开发的求解器能够准确模拟分离以及尾迹区的复杂流动,并有较高精度。
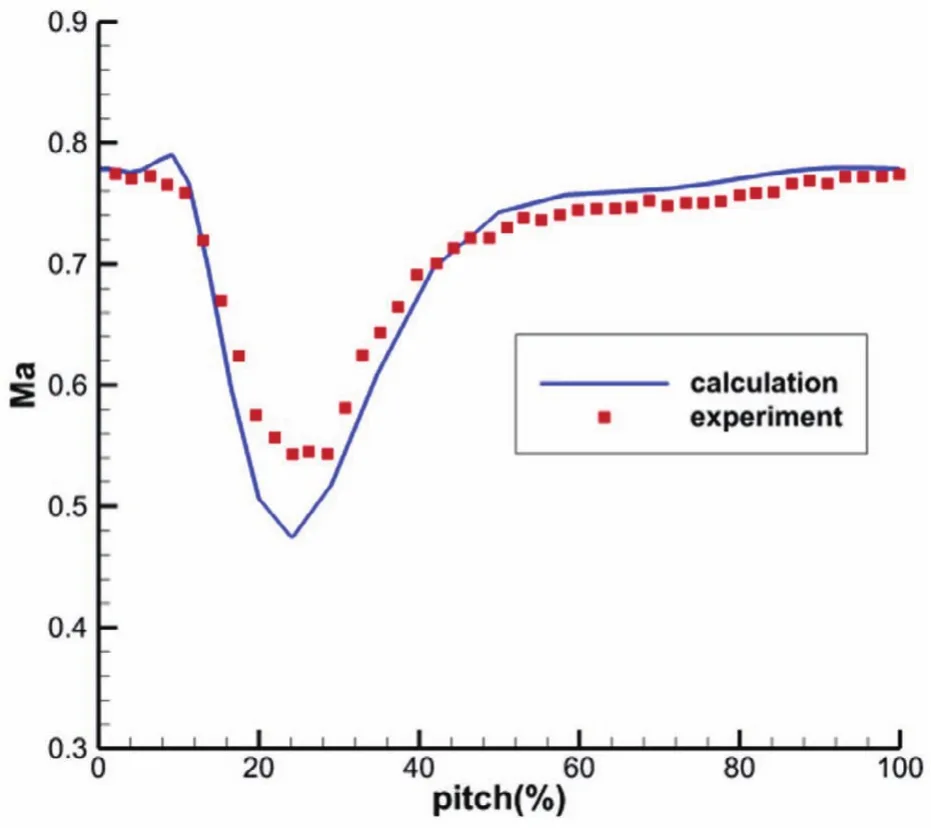
图5 98%堵塞流量工况转子出口50%叶高叶片通道相对马赫数分布
5.结论
本文给出了圆柱坐标系下采用JST格式的S-A湍流方程求解数值方法,以及滑移壁面函数的应用。对NASA Rotor 37转子开展了数值模拟,通过与试验数据对比,计算结果显示求解器对高负荷叶轮机特性预测精度较高,较好的捕捉了叶片尾迹,验证了本文数值程序的正确性和精度,表明本文所采用的方法对跨声速转子流场有较高的预测精度,能够满足工程精度要求。

