绝热条件下固体氧化物燃料电池的瞬态电化学特性

王朝阳，刘明，赵永亮，种道彤，严俊杰

（西安交通大学动力工程多相流国家重点实验室，西安 710049）

0 引言

2020年第75届联合国大会上，我国向世界郑重承诺，力争在2030 年前实现碳达峰，努力争取在2060 年前实现碳中和［1］。同年12 月，在气候雄心峰会上，我国宣布为实现“双碳”目标采取了一系列新举措［2］。随后，国务院发布了《新时代的中国能源发展》白皮书，明确指出我国未来将构建“多元清洁的能源供应体系”［3］。为此，我国将持续增加风能、太阳能等可再生能源的装机规模［4］，而风能、太阳能等可再生能源发电具有间歇性、周期性等特点，难以依靠自身保证持续稳定的电力供应。为提升可再生能源的利用效率和技术水平，可在能源系统内耦合储能设备，增强系统运行的灵活性［5］。

固体氧化物燃料电池（SOFC）是一种既可运行于发电模式，又可运行于电解模式的能量转换装置［6-7］。SOFC 在发电模式下能将H2，CH4等碳氢燃料的化学能通过电化学反应转化为电能，在分布式能源发电、小型发电设备及移动电源等领域具有广阔的应用前景［8］。SOFC 的逆过程为电解过程（SOEC），可将H2O，CO2等电解为H2，CO 等，将电能转化为化学能［9-10］，进而实现电能存储，或将电网无法消纳的可再生能源电力转换为H2，CO 应用于工业界，提高可再生能源的利用规模和效率［11］。

SOFC 在化学能与电能的转换过程中，电化学过程伴随着热量的吸收与释放，进而影响其内部温度变化，运行温度反过来又会影响化学反应中各项电化学参数的变化。蒋先锋［12］介绍了SOFC 中的热力学和电化学原理，随后根据电池的伏安特性曲线对不同电流密度下的活化极化、欧姆极化和浓差极化进行了研究。Tikiz 等［13］针对平板式SOFC 电池建立了三维仿真模型，探究了运行压力等参数对电池电化学性能的影响。楚迪［14］研究了顺流板式SOFC分别以H2和CH4为燃料时，沿着工质流动方向电池内部的温度、组分浓度、电流等关键参数的分布特性。Wu 等［15］基于高阶滑模观测器提出了一种复合非线性控制器，用于缓解SOFC 电堆在负荷变动时内部温度梯度大等问题。

目前，针对SOFC 热力学、电化学特性的研究主要集中在非绝热条件下的稳态热力学及电化学特性，对绝热环境下功率变化、电解与发电模式切换等瞬态过程的热电耦合特性研究却十分有限。为此，本文建立了SOFC 电堆动态模型，针对SOFC 电堆在绝热工况下的瞬态热力学和电化学特性进行研究，为SOFC 电堆在未来大规模应用时电堆运行热管理和能量高效转换利用提供参考。

1 SOFC动态模型

1.1 模型假设

SOFC单电池简化结构如图1所示，燃料和氧气分布在电解质两侧，当电池中有电流通过时，电解质中发生化学反应，完成化学能与电能的相互转化。SOFC 电池分为燃料侧、电解质和氧气侧，其中：燃料以流量qn，fuel，in进入燃料电极，以流量qn，fuel，out流 出；氧 气 以 流 量qn，oxygen，in进 入 氧 气 电 极，以 流 量qn，oxygen，out流出；电化学反应发生时放出热量Qreaction，向燃料散热Qfuel，向氧气散热Qoxygen。

图1 SOFC基本单元简化结构Fig.1 Simplified structure of a basic unit in the SOFC

本文建立了SOFC 电堆模型，该电堆模型主要由热力学和电化学模型耦合而成［16］。电堆模型的基本假设如下：（1）电堆采用集总参数模型；（2）工质为理想气体；（3）忽略电堆内部流体压力损失；（4）电堆内部各通道工质混合均匀；（5）忽略电堆运行过程中的衰减。

1.2 模型控制方程

SOFC电堆由N个相同的单电池片组成，在本文中N=8。电堆动态模型控制方程见表1，主要包含质量守恒方程、动量守恒方程、能量守恒方程以及电化学控制方程。表中：Mi为电堆内工质i的物质的量，mol；q˙n，i，in为进入电堆工质i的摩尔流量，mol/s；q˙n，i，out为流出电堆工质i的摩尔流量，mol/s；q˙n，i，react为电堆工质i参加化学反应产生的摩尔流量，mol/s；φ为系数，当反应生成工质i时φ=1，当反应消耗工质i时φ=-1；Rr为流道阻力系数；pin为电堆内部压力，MPa；pout为电堆外部压力，MPa；cs为电堆比热容，J/（kg·K）；ms为电堆质量，kg；hin为进入电堆的工质比焓，J/mol；hout为离开电堆的工质比焓，J/mol；W˙s为电堆发电量，W；Q˙s，react为堆内化学反应热，W；P˙s，int为堆内产热功率，W；ΔS0为标准摩尔熵，J/（mol·K）；P˙ext为电堆与外部热量交换功率，W；Q˙react为1 mol 工质发生化学反应产生的热量，W；N为电堆包含的单电池片数；Acell为单电池有效面积，cm2；Asur为电堆表面积，cm2；σ为斯蒂芬-玻尔兹曼常数；J为电堆电流密度，A/cm2；J0为电堆极限电流密度，A/cm2；Ts为电堆温度，K；Tf为电堆外部环境温度，K；ΔG0为吉布斯自由能变，J/mol；pO2为电极流道内氧气分压力，MPa；pH2为电极流道内氢气分压力，MPa；pH2O为电极流道内水蒸气分压力，MPa；α为电子传递系数；n为化学反应过程中1 mol反应物转移的电子的摩尔数；Vcell为电池输出电压，V；Vact为电池活化极化电压损失，V；Vohm为电池欧姆电压损失，V；Ras为面比电阻，Ω·cm2；Vconc为电池浓差极化电压损失，V；F为法拉第常数；ENernst为电池能斯特电压，V；角标tpb代表三相点；角标fuel代表燃料电极侧；角标oxygen 代表氧气电极侧。

本文采纳的SOFC 电堆结构和运行参数见表2。基于表1的控制方程，将各微分方程进行数值差分，自编程完成模型建立。将表2中电堆的相关参数代入模型，完成模型调试。动态模型验证部分已在作者之前的工作中进行了详细描述，电堆温度、电压和功率等关键参数的相对误差可控制在1%以内［16］。

表1 电堆动态模型控制方程Tab.1 Governing equations for the stack dynamic model

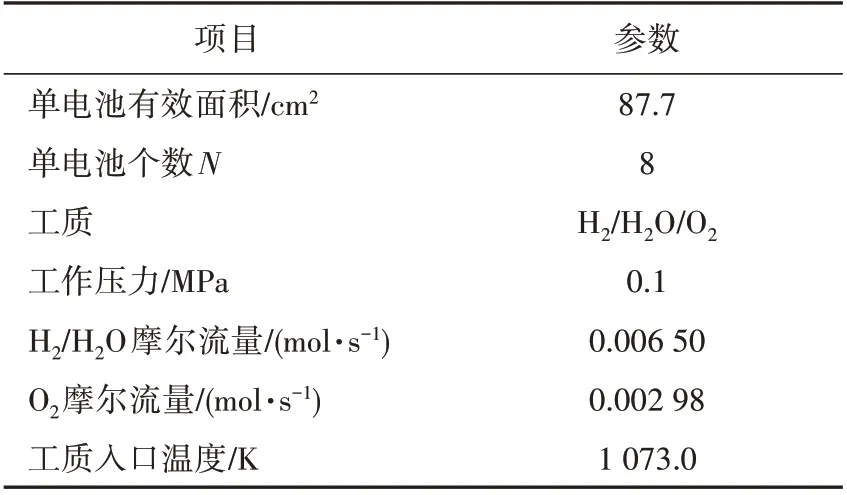
表2 SOFC电堆参数Tab.2 Parameters of the SOFC stack

2 SOFC电堆瞬态电化学特性

以SOFC 电堆定温（Ts=1 073.0 K）运行时电堆单电池内各项电化学指标为参照，对比分析绝热条件下SOFC 电堆内发电模式与电解模式切换的瞬态过程中，电池能斯特电压（ENernst）、电池活化极化电压损失（Vact）、电池欧姆电压损失（Vohm）、电池浓差极化电压损失（Vconc）和电池输出电压（Vcell）的变化情况。

训练数据集中有19种特征，其中特征7-13、15-17的值在测试数据集中被隐藏，特征14(Correct First Attempt)为需要预测的分类特征。因此，在训练过程中也排除了特征7-13和特征15-17。我们将剩下的8种非类别特征分为三类，一是与学生相关的特征，即特征2；二是与题目相关的特征，即特征3-6；第三类是与知识点相关的特证，即特征18和19。在对数据样本进行距离度量过程中采用协同过滤算法，把学生当做主体，即协同过滤算法中的客户，将题目和知识点看作与客户相关的项目。

本文研究了SOFC 电堆分别以斜坡和阶跃形式在电解和发电模式之间进行切换的过程中，电池的瞬态电化学特性。电堆运行前，初始温度为1 073.0 K，电流密度为0，电堆内O2电极通道O2体积分数为100%，燃料电极通道H2和H2O 体积分数分别为50%。电堆运行的边界条件见表2。

2.1 电流斜坡变化

如图2 所示，电流的变化总周期为4t0（t0=10 000 s）：0＜t＜t0时，电流密度J以斜坡变换方式从0 变为-0.25 A/cm2；t0＜t＜2t0时，J从-0.25 A/cm2回 到0；2t0＜t＜3t0时，J从0 增至0.25 A/cm2；3t0＜t＜4t0时，J从0.25 A/cm2回到0。

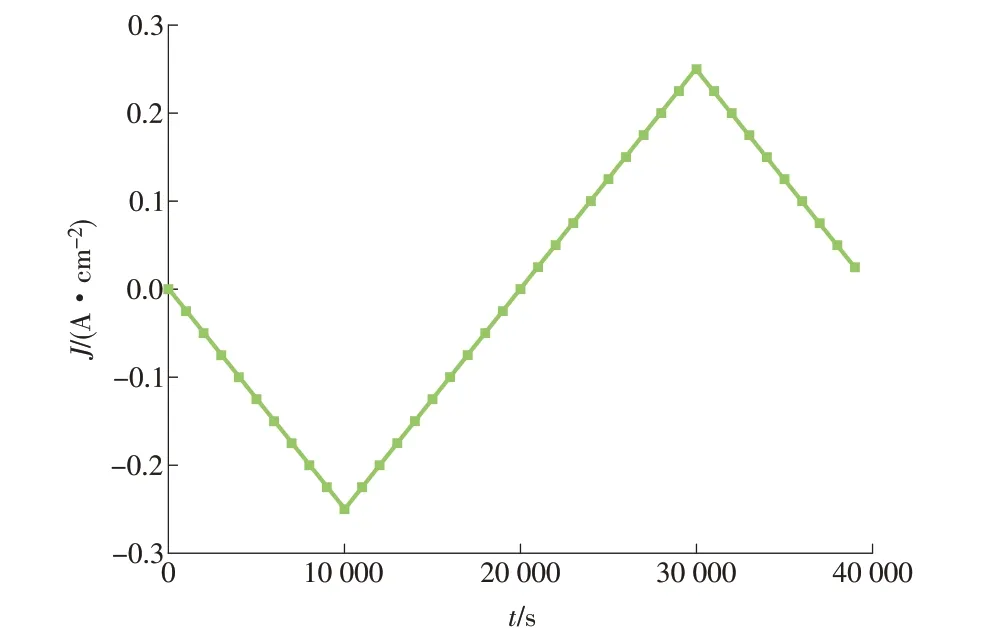
图2 电流密度斜坡变化Fig.2 Current density variation in ramp format

图3—8为SOFC电堆在绝热环境和定温环境下进行电解和发电模式切换的瞬态过程中，电流密度以斜坡形式变化时Ts，ENernst，Vact，Vohm，Vconc和Vcell的变化趋势。

如图3 所示，当J逐渐变为-0.25 A/cm2时，电堆运行在电解模式（SOEC），堆内的化学反应吸热，Ts从1 073.0 K 逐渐降低。0＜t＜t0时，随着J的增大，堆内电化学反应速率加快，Ts的下降速率逐渐增大；t0＜t＜2t0时，随着J的减小，堆内电化学反应速率降低，Ts的下降速率逐渐变小；当2t0＜t＜3t0，电堆运行于发电模式（SOFC），随着J的增加，Ts升高速率增大；当3t0＜t＜4t0，Ts的升高速率逐渐变小。t=4t0，电堆完成SOEC 到SOFC 模式切换的1 个周期，Ts先降至1 044.1 K，随后逐渐增至1 089.9 K，1 个周期内温度差达45.8 K，1 个周期后电堆温度较初温（1 073.0 K）增加了16.9 K。

如图4 所示，电堆在定温条件下时，ENernst与J之间一一对应，结合图3 中Ts的变化规律，在0＜t＜3t0范围内，在绝热边界条件下，Ts＜1 073.0 K，根据能斯特电动势的计算方法，绝热状态下的ENernst比定温（Ts=1 073.0 K）下的数值高，最大相差0.007 9 V；当3t0＜t＜4t0，ENernst比定温（Ts=1 073.0 K）下的数值低，最大相差0.004 8 V。

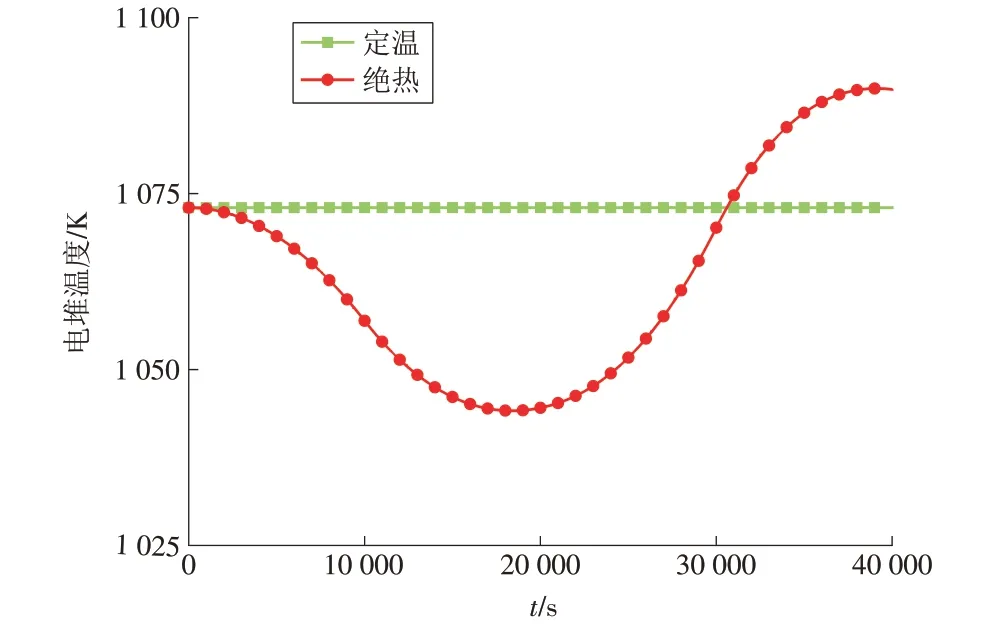
图3 SOFC电堆温度1Fig.3 Temperature 1 of the SOFC stack

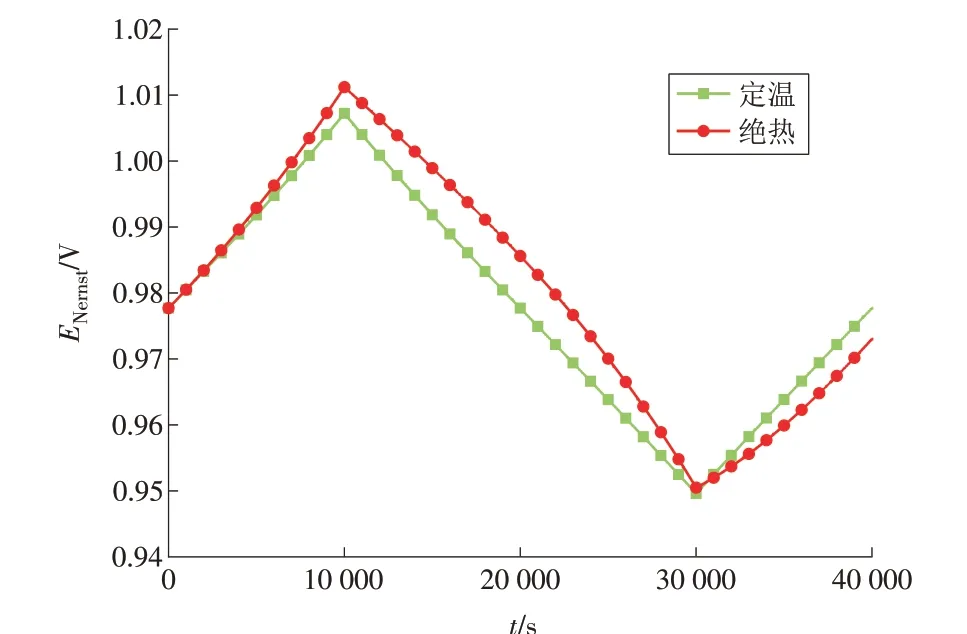
图4 电池能斯特电动势1Fig.4 Nernst EMF 1 of the cell

由图5 可知，电池的活化极化电压损失Vact与J成正相关：定温条件下，Vact与J成正比；燃料电池在经历SOEC 和SOFC 模式变化过程中，Vact受J与Ts的共同影响。从图5 可知，当t=t0时，J=-0.25 A/cm2，绝热条件下的Vact比定温条件下大0.005 V。

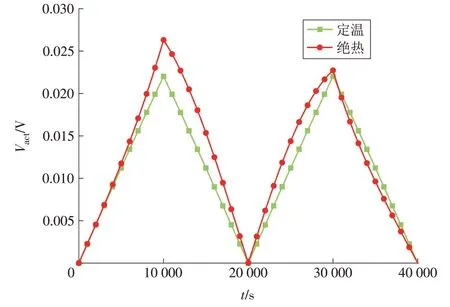
图5 电池活化极化电压损失1Fig.5 Activated polarization voltage loss 1 of the cell

如图6所示，在模式切换的瞬态过程中，燃料电池的欧姆电势损失Vohm变化趋势与Vact十分接近，当t=t0时，J=-0.25 A/cm2，绝热条件下的Vohm比定温条件下的数值大0.010 V。

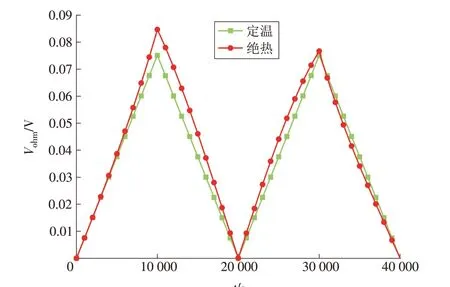
图6 电池欧姆极化电压损失1Fig.6 Ohmic polarization voltage loss 1 of the cell

由图7 可知：在本文的工质流量和电流密度边界条件下，与Vohm和Vact相比，Vconc的数量级较小；电堆温度对Vconc的影响较小。在本文的研究范围内，发电和电解时的各类工质在电堆内部相对充足，Vconc的数值相对较小。如图8所示，在模式切换过程中：Vcell受J和Ts共同影响，当J相同时，Ts越高，Vcell越低；当J相同时，绝热和定温运行对Vcell的影响最大相差0.014 V。

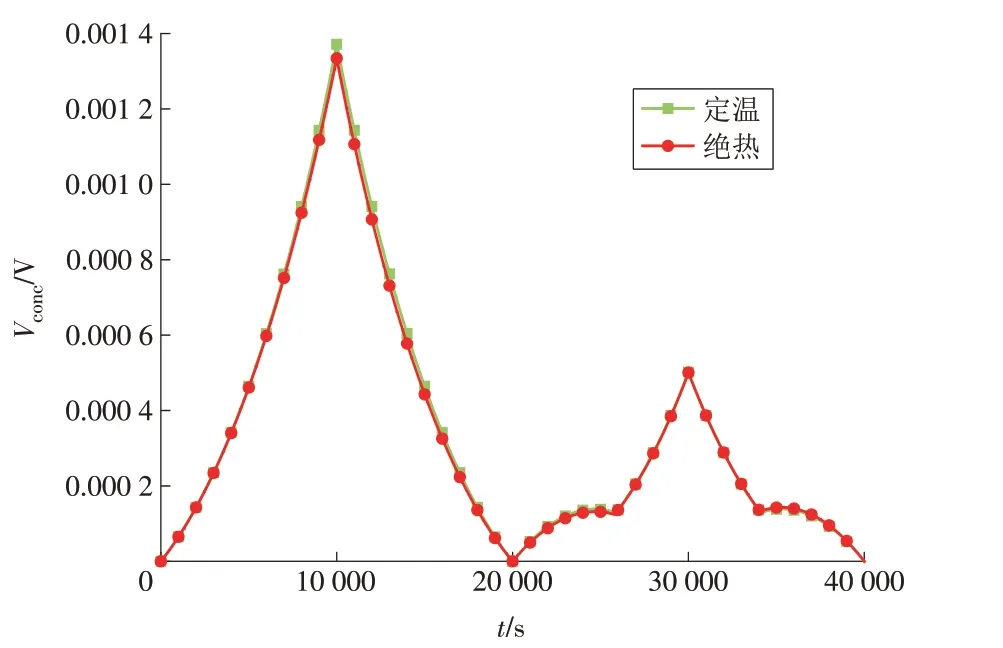
图7 电池浓差极化电压损失1Fig.7 Concentration polarization voltage loss 1 of the cell

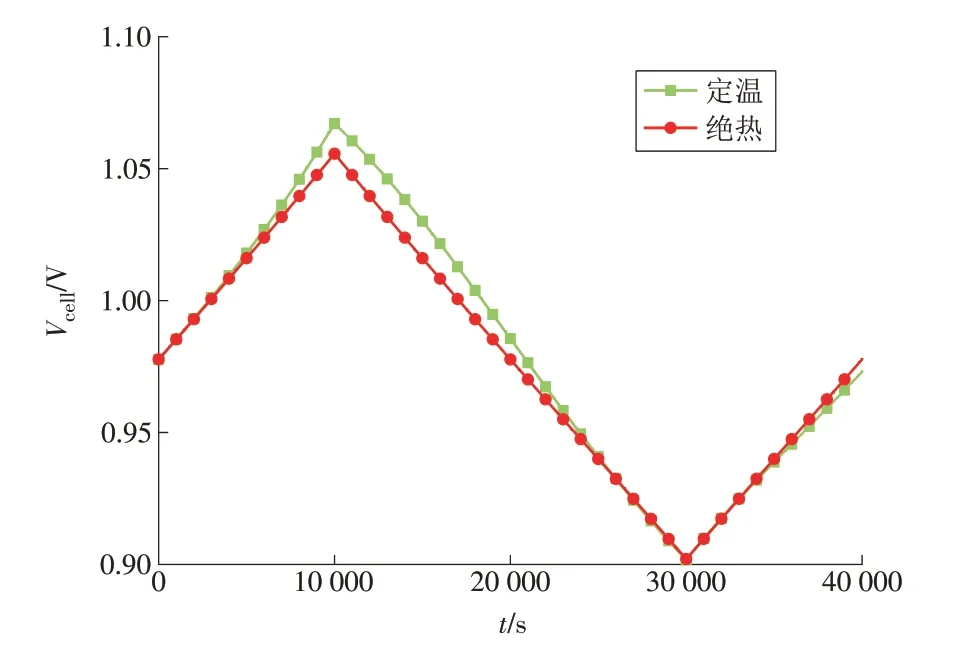
图8 电池输出电压1Fig.8 Output voltage 1 of the cell

2.2 电流阶跃变化

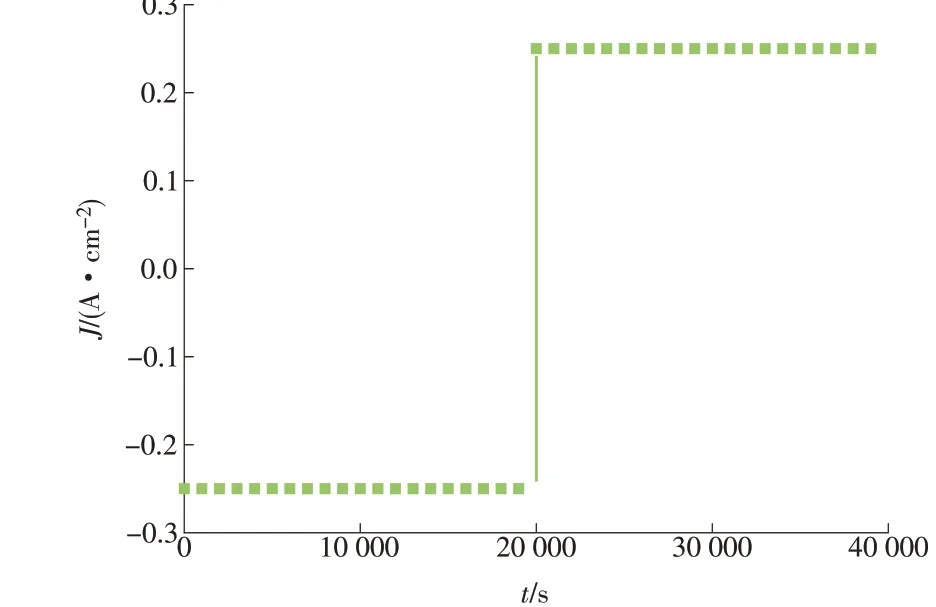
图9 电流密度阶跃变化Fig.9 Current density variation in step format

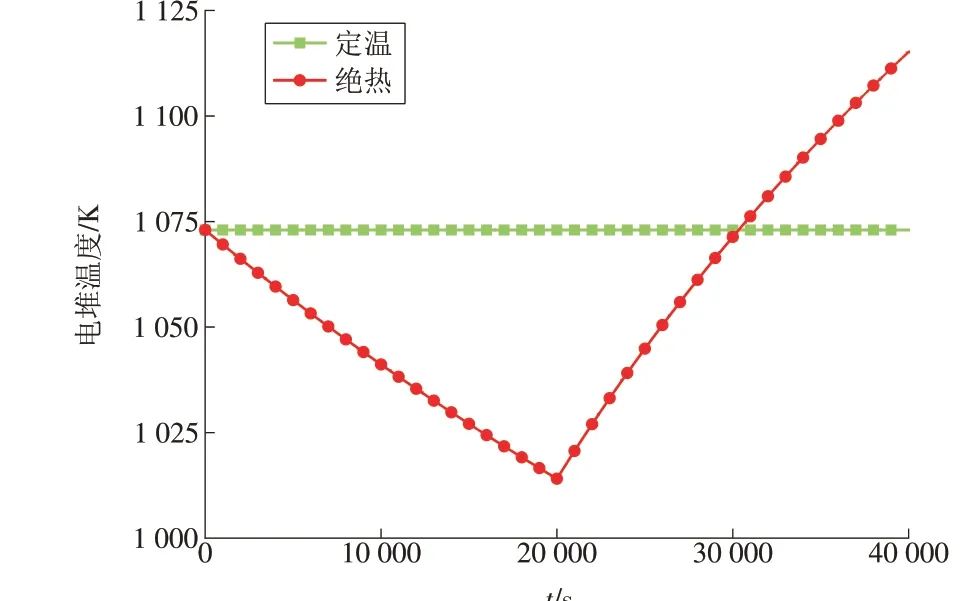
图10 SOFC电堆温度2Fig.10 Temperature 2 of the SOFC stack

如图11 所示，电堆在定温条件下（Ts=1 073.0 K）运行时，ENernst与J的数值和方向有关，当J大小不变，方向改变时，ENernst瞬间发生变化。电堆在绝热环境运行时：SOEC 模式下，Ts逐渐降低，ENernst随着Ts的降低而增加，从1.007 V 增至1.022 V；SOFC 模式下，Ts逐 渐 升 高，ENernst随 着Ts的 升 高 而 降 低，从0.985 V降至0.937 V。

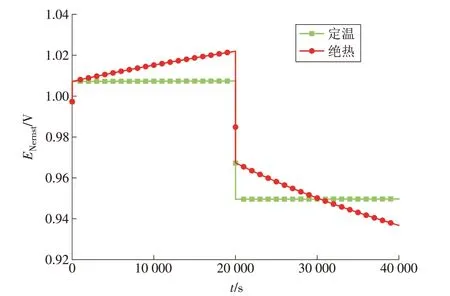
图11 电池能斯特电动势2Fig.11 Nernst EMF 2 of the cell

如图12 所示：SOEC 模式下，电流密度J=-0.25 A/cm2，0＜t＜2t0范围内，电池的活化极化电压损失Vact随着Ts的降低而增加，从0.022 V 增加至0.042 V；SOFC 模式下时，J=0.25 A/cm2，2t0＜t＜4t0范围内，Vact随 着Ts的 增 加 而 降 低，从0.042 V 降 低 至0.014 V。

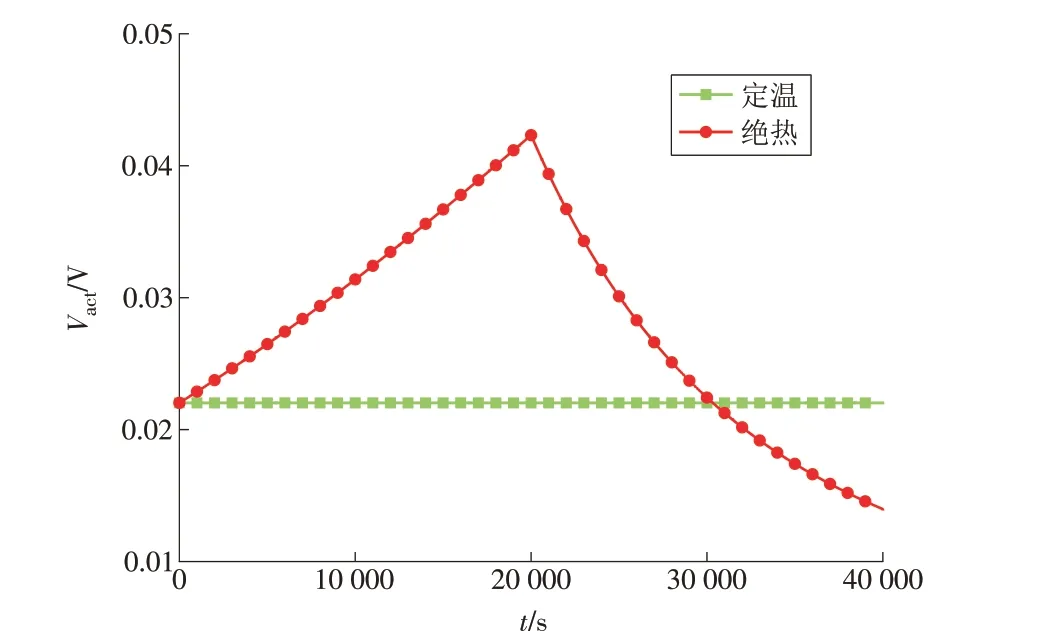
图12 电池活化极化电压损失2Fig.12 Activated polarization voltage loss 2 of the cell

由图13可以看出，燃料电池的欧姆极化电压损失Vohm变化趋势与Vact十分接近：在SOEC模式下，Vohm从0.075 V 增 至0.121 V；在SOFC 模 式 下，Vohm从0.121 V降至0.057 V。

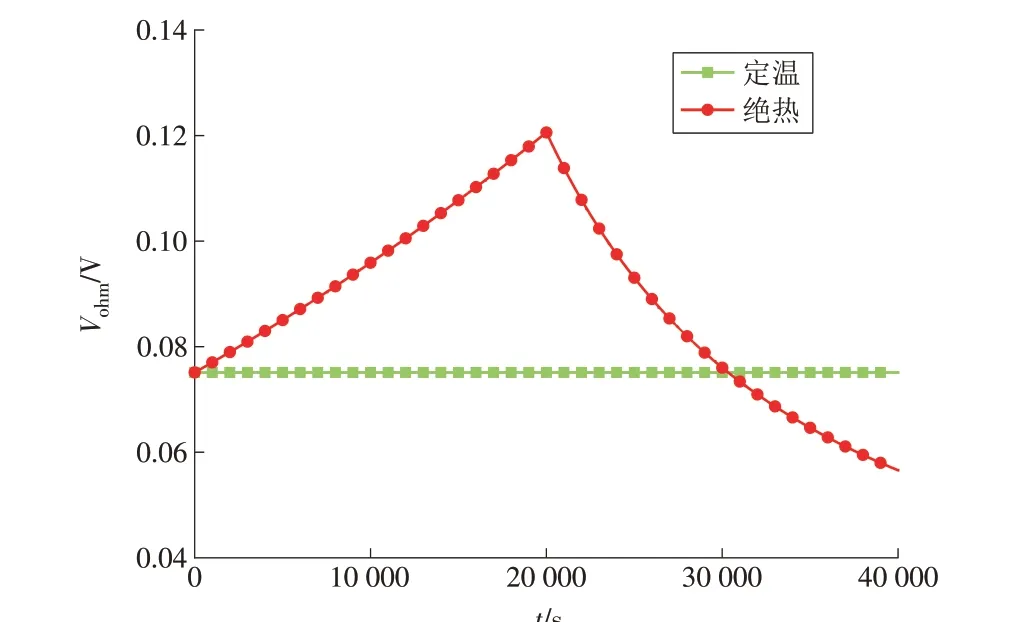
图13 电池欧姆极化电压损失2Fig.13 Ohmic polarization voltage loss 2 of the cell

如图14所示，电流阶跃变化的瞬间，Vconc瞬间降至极小值，随后在很短的时间内上升到相对稳定的数值，这是由于电堆内燃料通道内部有H2和H2O；当模式由SOEC 转换为SOFC 时，H2的摩尔分数瞬间增大，Vconc瞬间发生变化，由于电堆内的容积很小，在很短的时间内Vconc可到达新的稳定状态。温度同样影响Vconc：电堆运行于SOEC 模式时，在绝热边界条件下，Vconc随着电堆运行温度的降低而减小；电堆运行于SOFC 模式时，在绝热边界条件下，运行温度对Vconc的影响较小。

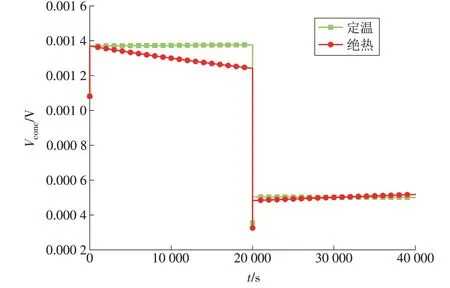
图14 电池浓差极化电压损失2Fig.14 Concentration polarization voltage loss 2 of the cell

由图15可以看出：电堆在SOEC模式下运行时，随着Ts的降低，Vcell逐渐升高，0＜t＜2t0范围内，电流密度J=-0.25 A/cm2时，绝热和定温运行对Vcell的影响最大相差0.050 0 V；电堆在SOFC模式下运行，随着Ts的 降 低，Vcell逐 渐 升 高，2t0＜t＜4t0范 围 内，J=0.25 A/cm2时，绝热和定温运行对Vcell的影响最大相差0.001 8 V。

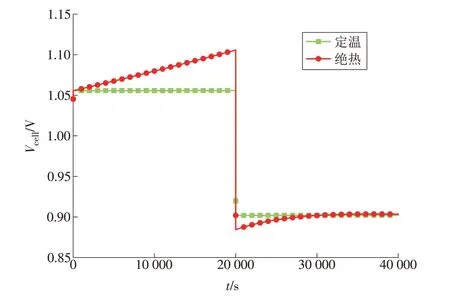
图15 电池输出电压2Fig.15 Output voltage 2 of the cell

综上可知，电堆运行温度影响固体氧化物燃料电池内的电化学特性。在绝热条件下，当电堆运行于电解模式时，运行温度越低，单电池的ENernst越高，同时各项电压损失（Vact，Vohm，Vconc）也越大，最终输出电压Vcell随电堆温度（Ts）的降低而升高，致使电解过程中所需电能增加；当电堆运行于发电模式时，运行温度越高，单电池的ENernst越低，Vact，Vohm也越低，Vconc变化不大，最终输出电压Vcell随Ts的升高而增加，进而发电功率增加。由此可知，保证电堆在电解时的热量供应可减少电解所需电能，电堆在发电过程释放的热量有利于其发电功率的提升。

3 结论

本文建立了固体氧化物燃料电池动态模型，以模型为基础，获得了电堆在电解（SOEC）和发电模式（SOFC）切换瞬态过程中的电化学特性，结论如下。

（1）电堆在绝热条件下进行从SOEC 到SOFC 模式切换，当初始温度为1 073 K、电流密度变化范围为-0.25～0.25 A/cm2、切换周期为40 000 s 时：电流以斜坡形式切换，电堆温度变化范围为1 044.1～1 089.9 K；电流以阶跃形式切换，电堆温度变化范围为1 014.0～1 115.2 K。

（2）电堆运行温度对电池的能斯特电压、活化极化电压损失、欧姆电压损失、浓差极化电压损失和输出电压等具有较大的影响；电流密度相同时，电堆在绝热条件和定温条件下运行时，单电池输出电压最大相差0.015 V。

（3）在电堆模式切换瞬态过程中，堆内工质摩尔分数影响电池的浓差极化电压损失，但由于电堆内的容积有限，在数秒内电堆的浓差极化电压损失会迅速达到新的稳定值。