基于有限元模拟的汨罗市泥石流发生机理研究及该区域风化砂土剪切特性考察
周 飞,王 磊
(山东正元地球物理信息技术有限公司,山东 济南 250101)
0 引言
泥石流是我国仅次于滑坡、崩塌的第三大地质灾害,严重影响了山区居民的生命财产安全、山区资源可持续发展以及山区工程的建设和维护,每年造成直接经济损失达数十亿元[1-4]。2016年7月4日汨罗市川山坪镇玉池山村玉明片区陈家山组后山出现了多处泥石流,导致上千群众受灾,直接受灾损失高达782万元。泥石流成灾过程具有较强的偶然性和复杂性,时程变化特性显著,野外原型观测与模型实验存在较大困难,因此,构建合理的数值模型来反演和再现泥石流过程的复杂物理现象逐步成为泥石流研究的有效手段。基于离散介质的网格方法通常忽略了泥石流运动中的流体特性,仅适用于含水较少的碎屑流模拟[5-6]。基于连续介质网格法发展较为成熟,与GIS平台以及目前通用的数字高程模型结合程度较好,便于各类泥石流本构模型与流量、侵蚀模型整合[7-8]。
经野外调查发现,在汨罗市泥石流发生的源头区域,土体的种类构成以及其粒径分布往往具备不均匀性,而渗透性的差异大量存在,如风化岩和堆积物,其具有高渗透性,因此与透水性能较差的岩层有一定的差异,此时不能渗入基岩的雨水在渗透和非渗透层的边界流动,并导致流入土体和地面塌陷的现象,参与到原始泥石流沉积物中形成大规模的地质灾害[9-11]。而大量的调查报告表明,管流孔道的痕迹大量出现在泥石流的源头部,这可能是后期导致泥石流发生的重要原因。管流的特性,流动和水压对安全系数和边坡崩坏的影响尤为显著,也是当前需要不断进行深入研究的着力点。当前大量的研究基于有限元法的理论基础,通过渗流分析对存在管流的坡面的地下水流向进行了讨论[12-14]。研究结果表明:管道中粗粒部分和孔道的堵塞引起的局部水压变化可能导致坡面塌陷,但孔道本身的结构和管道中泥沙的运动过程的结论尚未统一。
本研究中,暂时不对管流现象的产生与否进行讨论,利用有限元数值模拟,从压力水头,总水头差,流速等角度对边坡破坏机理进行详细分析探讨,对汨罗市玉池山村泥石流发生进行了有效再现和破坏机理分析。同时通过室内剪切试验对上部软弱风化土层的物理力学性质进行了分析,该分析对泥石流源头滑坡安全率理论计算具有重要作用,同时对该区域地质灾害预警和防治具有重要意义。
1 有限元渗透模拟
1.1 概述
本节通过有限元渗流模拟,以把握渗流速度和地下水水头,分析崩塌原因。在数值模拟中,把风化土层厚度、边坡坡度、表层条件作为变量。
1.2 泥石流特征整理
以汨罗市玉池山村泥石流的斜坡为模型,调查发现该斜坡具有以下特点:
地质条件:发生泥石流的地区以中生代白垩纪形成的花岗岩为主。花岗岩硬岩暴露在附近的山区,砂土化的风化堆积物稀薄地分布在山谷中。
地形:中游的河道为约5°的缓坡,裸露出花岗岩基岩(图1a)。泥石流末端区部分堆积物主要由砂土组成,即使在2°~3°以下的缓坡,也发生了250~400 m的流动距离(图1b)。
源头区域状况:泥石流源头部崩塌平均深度为1.5 m或更小,坡度多为25°~40°,尤其集中在30°~35°范围内。在风化层与基岩的交界处,有粗粒沉积物分布,说明渗透性较强(图1c)。

图1 区域现场拍摄图像Fig.1 Field images in the area
1.3 数值方法、模型和案例
根据1.2泥石流特征,建立边坡模型,采用有限元法进行二维渗流数值模拟。
1)土层构成和初期条件设定。通过对泥石流发生边坡的野外勘察,发现表层土没有或者很薄。其次,由于发现风化的砂土层与花岗岩基岩的交界处夹杂一层具有高渗透性的粗粒层,推测为以往泥石流的堆积物。数值模拟将分别在风化砂土层上有/无表土层的情况、风化砂土层部分分布表土层的情况、风化层与基岩之间有/无高渗透层的情况结合进行分析。关于非饱和渗透性,图2中表示了体积含水率θ与负压水头ψ的关系、体积含水率θ与比渗透系数Kr的关系。各土层的渗透特性见表1。采用线弹性模型进行数值分析,风化砂土的弹性模量设为10 MPa,泊松比为0.3,条件为排水。由图2和表1可知,在深度方向的吸力分布设置为0,并且未设置初始地下水位。

图2 非饱和渗透特性Fig.2 Unsaturated permeability characteristics

表1 各土层特性Table 1 Characteristics of each soil layer
2)坡度。参考发生泥石流的状况,将斜面坡度设置为25°,中游坡度设置为5°,不易发生泥石流的条件。
3)降雨量与边界条件。将表2中从2016年7月4日湖南省汨罗市观测到的降雨量作为降雨条件。在这种降雨条件下,泥石流产生于上午7:00至8:00之间。由图3可见,给模型的左右两边设置一定水头(右边20.0 m,左边至表土下),模型底部为排水面。在本数值分析中,采用恒定流量渗透边界。为了便于与真实降雨变化情况进行对比分析,默认模拟开始时间与真实降雨开始时间一致,即为凌晨1:00,之后进行时间累计分析。
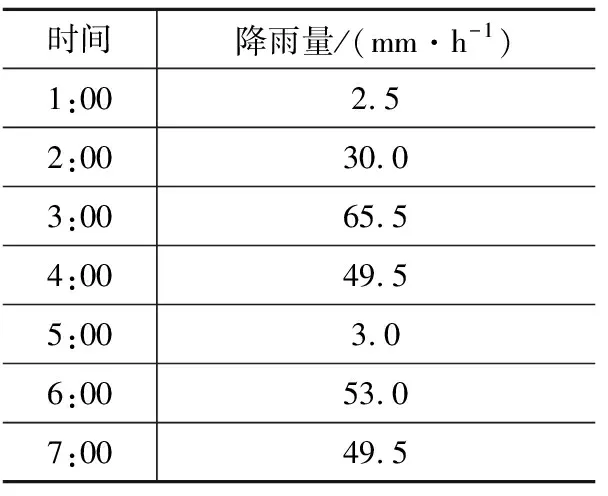
表2 2016年7月4日汨罗市山区降雨Table 2 Rainfall in the mountainous area of Miluo City on July 4,2016
根据现场勘察情况,对表3和图3中所示的5种情况进行了数值分析。
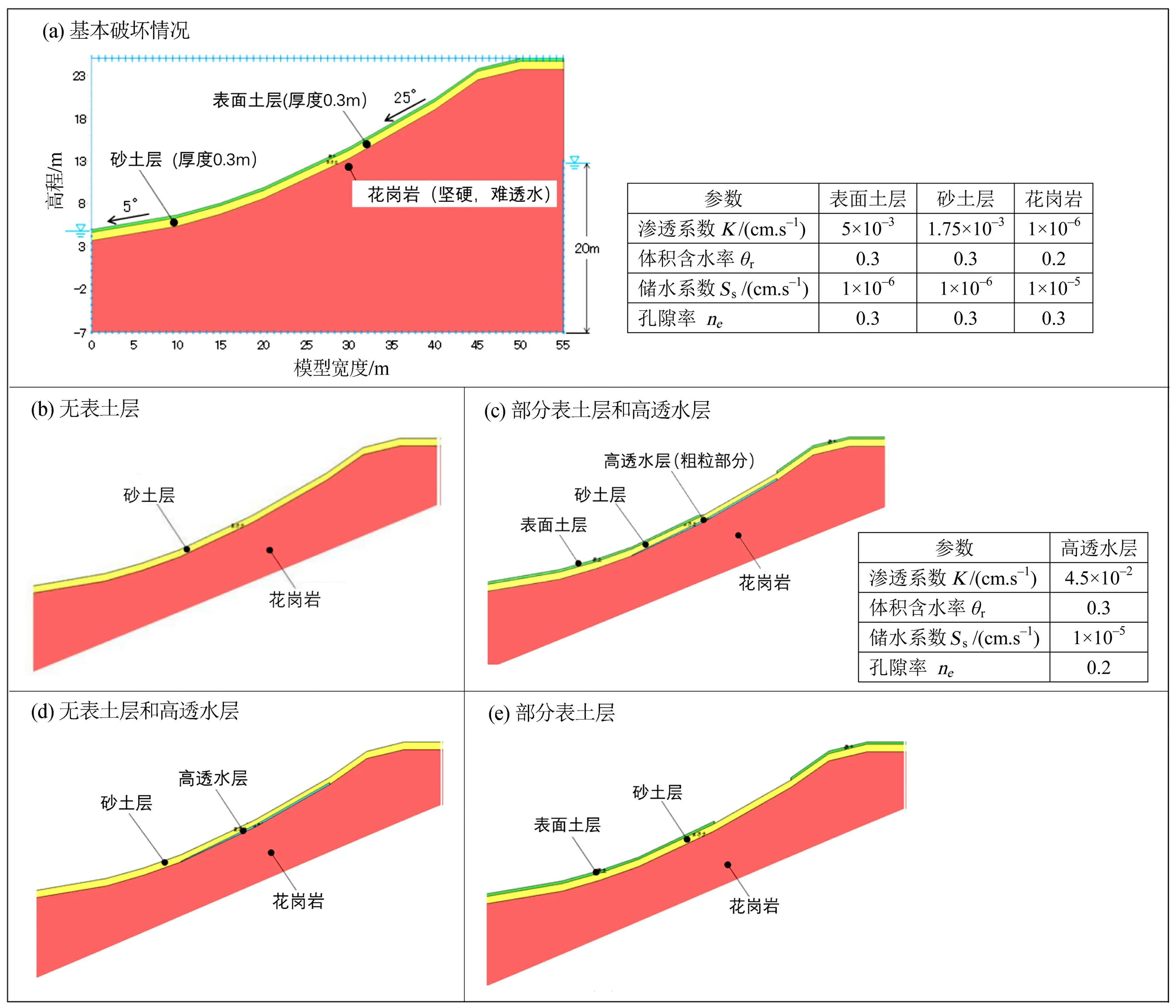
图3 边坡模型Fig.3 Slope model

表3 有限元数值分析案例Table 3 Finite element numerical analysis case
2.4 数值模拟结果
分别对表3中五类工况进行分析,边坡模型为长55 m、地下水位线右侧20 m处。图4为各次降雨开始后5.5 h的上午6:30边坡内水头分布情况。由图4a可见,如果有表层土壤但没有高渗透层,即使给以大量降雨,压力水头也不会随着时间的推移而发生剧烈变化。
另一方面,表土完全不存在的工况b中,图4b中,压力水头为0,即地下水位不规则地出现在边坡中,这种情况已经无法用达西法则来解释说明。这种状况是从凌晨2:00的降雨引起的,无法解释7:00到8:00泥石流的发生。

图4 有限元模拟结果Fig.4 Finite element simulation result
在缺少部分表土的工况c和工况e情况下,残留表土在这两种情况下都会抑制渗透,斜坡内的渗流相对稳定。在工况c和工况d中,无论有无表土,在高渗透层中都会发生比其他情况更快的渗流,压力水头随也会时间增加而增加。特别是图5中工况d时,4:30以后,高渗透性区域的压力水头逐渐增大。在分析初期,2:00时水头分布的不自然被看作是过渡现象,之后在3:00时开始变得稳定。
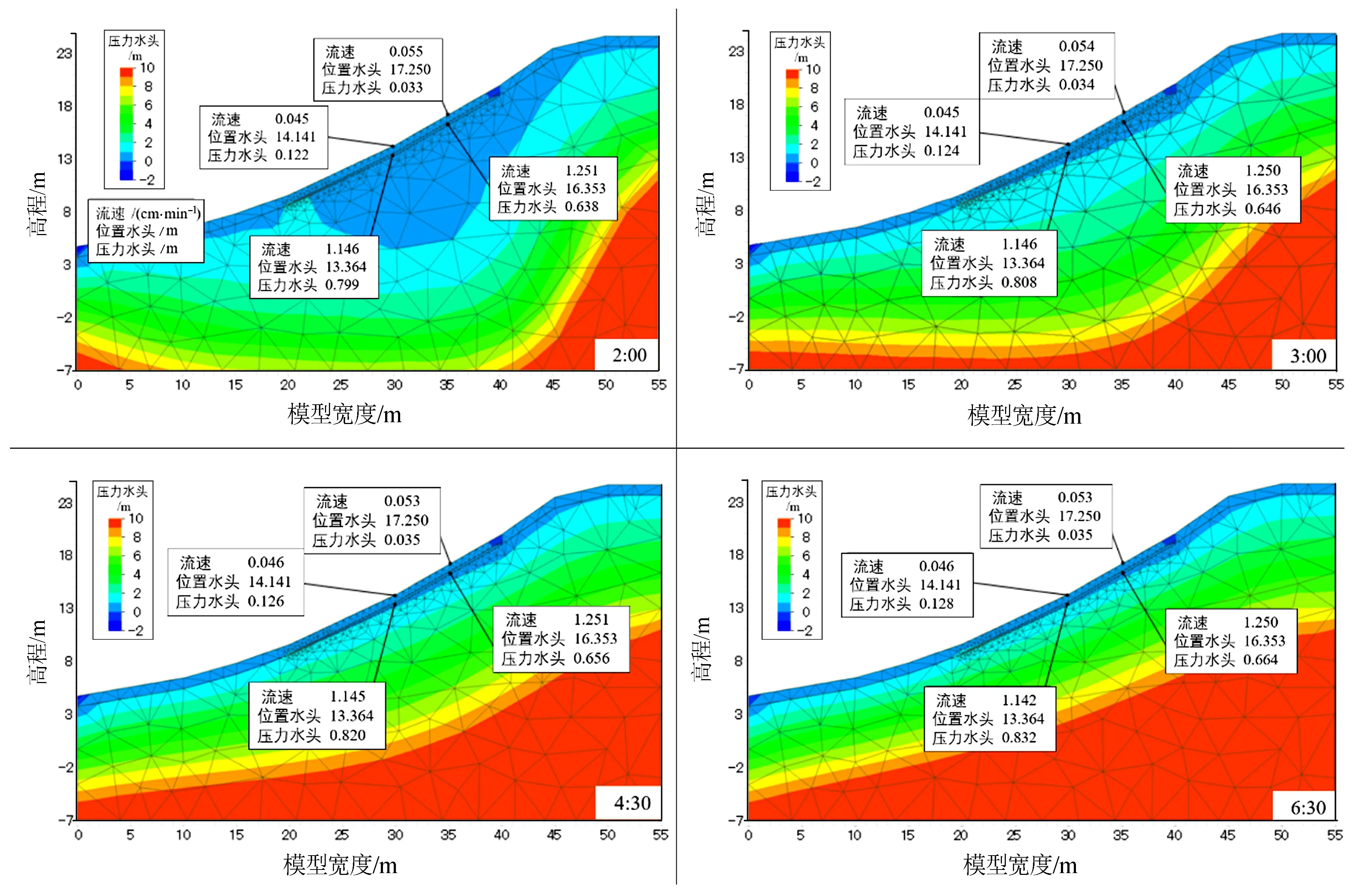
图5 工况d的经时变化Fig.5 Time variation in case d
表4为风化砂土层内部的流速、水头、安全率的计算结果。实际流速为观测1、2点的平均流速除以有效孔隙率的值。工况c和工况d的实际流速达到0.06 cm/s。本文采用经典的Taylor(1948)[15]极限流速ν计算公式(1),得到ν=1.78 cm/s。
(1)
其中:g为重力加速度;γs为土的浮重度;A为受到渗流作用土的横截面积;γw为水重度;Gs为土粒相对密度,取值2.62;d为粒径,D10= 0.003 cm。
可以推断出风化砂土层中的流速足够缓慢和稳定,不会因流速而导致渗透破坏。图4中两点(1点和2点)流土现象安全系数F用公式(2)计算[16]。压力水头最大的点为第2点,距第2点水平距离为5~10 m处上游点为第1点,计算结果见表4。
(2)
其中:e为孔隙比,0.8;ha为压力水头差;D为位置水头差。
由表4可知,只有在工况d中,没有表土,砂土层厚1.0 m,交界处有高渗透层,F才略低于1.00。第一次强降雨后的4:30分,F≥1.00,但第二次强降雨后的6:30,F<1.00,与泥石流发生时间一致。虽然没有因流速而发生渗流破坏,但认为由于压力水头的增加,边坡稳定性有所下降。

表4 观测点1和2的流速、水头、安全率Table 4 Flow velocity, water head and safety rate at observation points 1 and 2
3 风化花岗岩剪切特性考察
对于泥石流源头多处的边坡崩塌,本文数值分析从水头变化等角度对边坡稳定性进行了讨论,但仍需要从力学性质角度对边坡构成土层进行力学分析以及进下一步的边坡安全率计算等。本节通过直剪试验对汨罗市泥石流发生区域风化花岗岩滑动过程中的剪切特性进行了初步判定。
3.1 野外调查和土样采集
土样采集点位于汨罗市川山坪镇玉池山村玉明片区陈家山组后山边坡,坡度约30°。表层花岗岩风化强烈,地层组成以砂土为主。土样采集图片见图6,图7为原状土采集土筒的尺寸。

图7 原状土采集土筒Fig.7 Undisturbed soil collection tube
3.2 剪切仪概况
剪切仪见图8,土样盒直径6 cm,高2 cm,内部光滑,分为上下两层。剪切前进行超过20 min的压密,试验开始后维持同一垂直应力σ不变,保持0.2 mm/min的剪切速度,每隔1 min记录剪切应力τ,垂直位移ΔH和剪切位移δ。当剪切位移达到7 mm时终止试验(剪切仪剪切位移上限)。

图8 室内剪切仪Fig.8 Laboratory shear equipment
3.3 风化层物理性质
风化层物理性质详见表5,风化土层原状土土样抽取3个进行剪切试验。

表5 风化层物理性质Table 1 Physical property of weathered layer
3.4 剪切试验结果
图9中展现了风化土在自然含水比(Sr=37%)下,剪切应力τ、垂直位移ΔH和剪切位移δ关系。剪切过程中剪切应力τ没有出现明显峰值后下降的现象,到达一定值后趋于稳定。

图9 剪切应力-剪切位移关系(a),垂直位移(b)-剪切位移关系Fig.7 Relationship between shear stress and displacement (a), vertical displacement and shear displacement (b)
从体积变化角度来看,最主要展现了剪切过程中土样体积收缩的特性。剪切应力τ和垂直应力σ的关系见图10。

图10 剪切应力和垂直应力关系Fig.10 Relationship between shear stress and vertical stress
4 有限元模拟和剪切试验结果考察
在有限元分析结果中,每种工况下都得到了随着降雨的持续而出现的压头升高情况,但在工况d中,坡面无表土,且透水性有差异,即基底与砂层之间夹杂高渗透层,随着降雨量和时间的增加,观测点2的压力水头逐渐增大。本案例中,在计算安全系数时,在上午6:30,即降雨后5.5 h,得到F<1.00,推测有流土现象发生,可能由于以下原因造成:
首先,如果基底的岩层非透水,而表层土又不能抑制渗透,那么强降雨时,约1.0 m厚的薄砂土层会很快饱和。此外,由于表土没有覆盖整个坡面,且与基底的边界附近分布着粒径相对较大的高渗透层,随着降雨的不断进行,导致压力水头升高。到了一定程度,压力水头达到所谓的流土状态,土颗粒失去凝聚力,从而进一步导致崩坏发生。
在后续风化花岗岩土样剪切试验考察部分,初步得到了风化土层物理参数及其剪切特性,为今后边坡稳定性分析和理论研究提供重要参数支持。
5 结论
本研究通过数值分析在不同土层分布条件下,对汨罗市玉池山村泥石流发生进行了有效再现和破坏机理分析,有限元数值模拟和剪切试验得出的结论如下:
1) 对2016年7月4日汨罗市玉池山村泥石流灾害发生源头边坡进行数值分析,孔隙水压随土层构成不同而变化较大,当砂土层和不透水层之间存在粗粒高渗透层时,观察到孔隙水压急剧增加,造成坡稳定性下降。
2) 在无表层土和存在粗粒高渗透层的情况下,在第二次强降雨后,孔隙水压上升导致安全率小于1,边坡失稳。
3) 作为数值模拟水压变化的补充,进行了部分土的力学性质实验。在剪切试验中,风化花岗岩展现出剪切收缩特性,并初步得到了该风化土层物理力学性质,为下一步边坡稳定性分析奠定力学基础。
本研究对该区域地质灾害预警和防治具有重要意义,对于夹杂高渗透层导致管流和边坡流土发生的情况,今后研究中仍需边坡模型试验对数值模拟进一步对比分析。

