竞争和对抗背后的秘密——博弈是个啥?
闫升
最近,国内一些城市出现了一些按时间对商品进行打折促销的生鲜店。以Q店为例,该店从每晚19时开始打九折,并且每隔半小时降一折。湖南株洲的小吴居住的小区旁就有一家Q店。在得知这种打折模式后,他觉得其中有利可图,因为按照该店规定,晚上11点半店内所有商品都免费赠送。一天晚上,小吴打算去Q店买些打折肉。但让他没有想到的是,才到晚上9点(五折时分),店里的蔬菜就已经卖得一干二净,肉柜台只剩下几块很肥的五花肉。犹豫再三,他还是从中挑了一块,原价35元,打折后17.5元。

提出“纳什均衡”的约翰·纳什。
虽然以半价买到一块五花肉,但它是被挑剩下的,因此小吴并没有什么成就感。他很疑惑:为什么才到晚上9点,店内商品就几乎售罄?为什么大家不等到晚上11点半店家免费赠送商品呢?其实,没有消费者能在晚上11点半免费领到店中剩下的商品,而这是博弈论所预测的一种必然结局。美国数学家约翰·纳什将这样的结局称为“纳什均衡”,他也因提出“纳什均衡”模型而获得1994年的诺贝尔经济学奖。
博弈:通过竞争达到均衡
什么是博弈论?博弈就是竞争或对抗。小到猜拳、下棋和讨价还价,大到金融交易和国际关系,其实在整个人类社会和自然界都充满各方之间的博弈。博弈论研究的是博弈各方会怎么想和怎么做。博弈思想古已有之,《孙子兵法》就是诠释博弈思想的古代著作之一。进入现代,数学家开始系统研究博弈论。1928年,被誉为“计算机之父”的冯·诺依曼证明了博弈论的基本数学原理,也宣告博弈论成为一门正式学科。博弈论的核心在于:人或动物只有在考虑自己的同时预测其他参与者的行为,才能选出对自己最有利的方案。
纳什均衡又是什么呢?不妨以小区居民去Q店买菜来举例说明。在打折时段前,总有人会进店买菜。而Q店每天上架的蔬菜和肉类是有固定量的,卖完后不会补货,这意味着早去的消费者能挑选到品质最好的菜或肉,而越晚进店选择越少,甚至可能无菜可选。因此,在涉及生鲜品价格和品质的竞争中,永远不会出现消费者0元拿好菜的结局,而只会出现一些人原价买好菜、另一些人低价买劣菜的均衡结局,这就是一种纳什均衡。
纳什均衡的另一个例子是价格战。价格战虽违背了生意人的基本逻辑(以最小投入换取最大利润),却是一种最稳妥的生存之道。假设有甲和乙这两家超市。如果它们同时高价售卖商品,那么它们都能躺着赚大钱。但只要一方开始降价促销,另一方为了争夺消费者,就必须立刻跟上。作为博弈中的任何一方,是否降价会导致四种结局(这里只说明简化情况):一,双方都不降价,都会大赚;二,自己不降价而对方降价,自己会倒闭;三,自己降价而对方不降价,对方会倒闭;四,自己和对方都降价,双方都会小赚。可见,通过降价能保证自己100%生存下来,而不降价则有一定的倒闭风险,因此,任何一个理性的经营者都会选择降价。这样一来,同行之间的价格战在所难免。

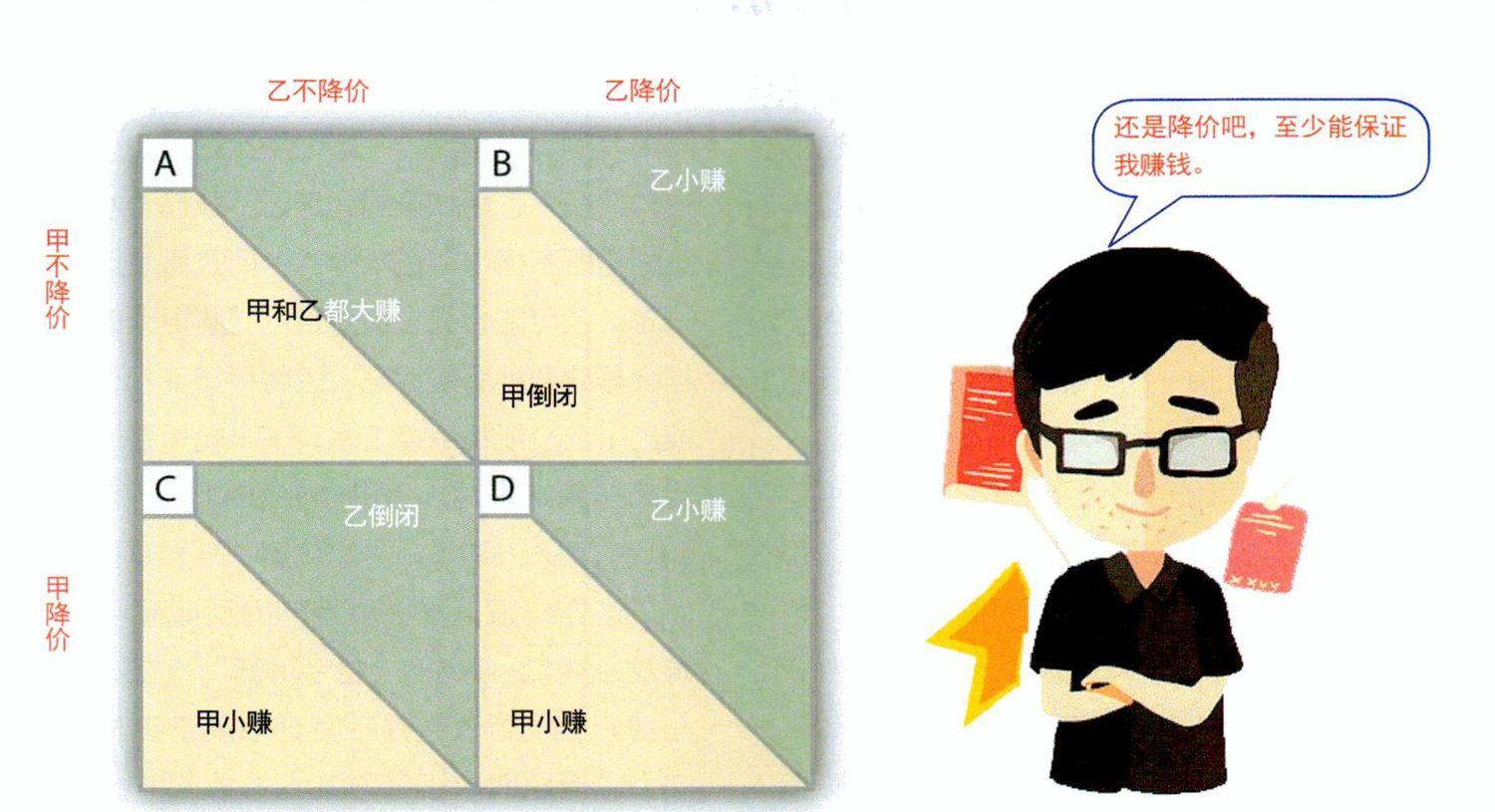
價格战双方的选择和收益表格
因为博弈中的各方无法控制其他所有参与者的行为,所以要保证自己收益最大化,各方必须采取折中但稳妥的方案,并且对所有人都最有利的结局是不可能达到的,这就是纳什均衡的核心思想。
智猪博弈:强者和弱者如何共存?
根据不同的博弈情景,纳什均衡的具体形式也分好几种,其中的“智猪博弈”尤为特殊。什么是智猪博弈?在一个狭长的猪圈中,生活着一头大猪和一头小猪。猪圈的一头是投食口,如果按下位于猪圈另一头的开关,投食口就会放出一定量的食物。这两头猪都有两种选择:要么在按按钮后跑到投食口,要么慢慢走到投食口并等待对方按按钮。大猪吃猪食的速度远远超过小猪,因此无论小猪是否主动按按钮,最后大猪都会吃掉大部分猪食。而如果小猪选择等待,那么大猪为了不被饿死,就只能选择主动去按按钮。在这种情况下,纳什均衡就是大猪按按钮,小猪守在投食口等待猪食。
智猪博弈可以说是现实生活中应用场景最广泛的博弈模型。在商业竞争中,开拓市场和创新的任务往往由资金雄厚的大企业承担,小企业则更愿意选择跟随和模仿大企业。这种纳什均衡能保证付出更多的大企业获得更多收益,而付出较少的小企业也能以最小的投入换回不错的收益。在企业中,会思考且努力的员工就像智猪博弈中的大猪,而懒惰且不愿思考的员工就像小猪。一般而言,虽然企业主会想方设法让员工更努力工作,但只要有大猪存在,就会有小猪的生存空间。

枪手博弈:胜负不光看实力
在水上乐园的平台上,有甲、乙、丙三人玩斗鸡游戏。他们单脚站立,用另一条腿撞击对方,落水就算失败。其中,甲玩得最好,每次撞击有80%的概率让对方落水;乙稍次,有60%;丙最差,只有40%。游戏规则是:每轮三人同时开始行动,且每人每轮只能撞一次。那么,最终谁赢得比赛?从命中率来看应该是甲,但结果不一定如此。
例如,甲可能会决定优先撞乙,理由是乙对自己威胁更大。如果乙和丙也这么想,那么他们会优先撞甲。必须乙和丙同时撞偏,甲才不会被撞下水,这种情况发生的概率为24%(60%×40%)。乙不被撞下水的概率为20%(1-80%)。而因为第一轮没有人会去撞丙,所以丙不会被撞下水。
如果改变规则,三人轮流撞击,为了照顾水平最差的丙,由丙先开始,那么结局会如何?在这种情况下,丙如果想让自己不被撞下水,最佳策略是既不撞甲,也不撞乙,而是假装撞偏。下一轮,乙可能会优先撞对自己威胁更大的甲。这样会导致两种可能情况:乙将甲撞下水,轮到丙撞乙;乙没能将甲撞下水,下一轮甲会撞乙……当第三轮结束后,甲继续站在平台上的概率为55.6%,乙为66.7%,丙为83.3%(推导过程从略)。
这样一来,水平最差的丙反而最可能赢得游戏,这就是著名的“枪手博弈”。它告诉我们,在博弈中能否获胜并不完全取决于参与各方的实力,而更取决于各方实力造成的彼此间的制约关系。

三人斗鸡示意图
竞争,淘汰物种也保护物种
为了生存,自然界的生物同样在进行着激烈的博弈。在博弈过程中,物种与物种之间会形成一种“剪刀石头布”型纳什均衡。
科学家一直想知道,为什么同一片栖息地中能够容纳许多物种?为什么没有一种超级物种能够完全排挤掉其他所有物种?以珊瑚为例,同一海域的珊瑚彼此之间的竞争十分激烈。有的珊瑚长得十分巨大,从而尽可能获得更多光照,并遮挡其他珊瑚的光照;也有珊瑚会通过触手中带毒的刺细胞,或喷出含有刺细胞的黏液,从而杀伤竞争对手。然而,就算某些珊瑚的竞争手段十分狠毒,也没有哪个品种的珊瑚能击败所有其他珊瑚。更有趣的是,珊瑚之间的竞争不但没有限制它们的生长,反而让珊瑚占据了其他不少物种的生态位——作為珊瑚的主要竞争物种,巨藻一般只出现在珊瑚多样性低的区域。
珊瑚之间的竞争就好像一场“剪刀石头布”游戏,没有绝对的强者,不同的珊瑚物种会轮流占据优势地位。随着珊瑚物种越来越丰富,它们采取的生存策略越来越复杂,整个大珊瑚礁生态系统的稳定性也越来越高。珊瑚礁越稳定,单一珊瑚物种完全死亡的可能性也会随之降低。因此。竞争和相互制约是珊瑚繁盛的秘密之一。
面对有限的空间和资源,竞争和对抗在所难免,这就是研究博弈论为何如此重要的原因。通过了解种种纳什均衡,我们可以知道有时候会追求不到最优结果:有时我们需要允许别人搭便车,有时我们要看清自己和别人的关系。同时,博弈思想又是复杂、变化的。例如,枪手博弈的大前提是所有人都已掌握关于自己和对方水平的信息,但如果某个高手故意隐藏实力,结果又会如何呢?

