Orientation dependence in high harmonics of ZnO with polarization corrections to counteract the birefringent effect*
Yin-Fu Zhang(张银福) Teng-Fei Huang(黄腾飞) Jia-Peng Li(李佳鹏) Ke Yang(杨可)Liang Li(李亮) Xiao-Song Zhu(祝晓松) Peng-Fei Lan(兰鹏飞) and Pei-Xiang Lu(陆培祥)
1School of Physics and Wuhan National Laboratory for Optoelectronics,Huazhong University of Science and Technology,Wuhan 430074,China
2Hubei Key Laboratory of Optical Information and Pattern Recognition,Wuhan Institute of Technology,Wuhan 430205,China
3CAS Center for Excellence in Ultraintense Laser Science,Shanghai 201800,China
Keywords: high-order harmonics,birefringent effect,Jones calculus
1. Introduction
High-order harmonic generation (HHG) in gaseous media has led to significant advances in the study of molecular electron dynamics on the attosecond time scales.[1-10]Because the information of the target structure is encoded in the HHG, a technology called molecular orbital tomography has been developed.[11-14]Recently,the developments of HHG in the solids have opened a new frontier in the ultrafast science.Since Ghimireet al.observed HHG in the ZnO crystal using mid-infrared (mid-IR) laser pulses,[15]harmonics generated from various crystals have been reported.[16-24]Similar to the HHG in the gases,the solid structures are related to the dependence of harmonic yields on the orientation of the crystal axis. Different from the gas-phase media,solids have periodic structures and can be precisely aligned to a certain orientation. It is expected to have great potential for band-structure reconstruction[25-28]and probing electron dynamics[29,30]by using the HHG in solids. Whereas, the harmonics in solids are coupled with the propagation effect, such as the absorption,phase mismatch of HHG,[31]and the birefringence of the crystals. It may affect the HHG in solids. However,the effect of birefrigence is not explored in previous works of HHG in ZnO.[20,32,33]
In the past several years,the propagation effect has been studied in some crystals.[31,34-37]In Ref.[36],Vampaet al.investigated the HHG in a reflection geometry with MgO and Si.They predicted the variation of the high-harmonic power with the angle of incidence by introducing the nonlinear reflection coefficients. By using both the reflection and transmission geometries,Xiaet al.studied the propagation effect in the HHG of GaAs.[37]They observed that the orientation dependence of HHG in the transmission geometry becomes more anisotropic for the thicker sample. In contrast,the orientation dependence of HHG in the reflection geometry is less anisotropic than that in the transmission geometry. When the laser pulses propagate through the crystal, the polarization can be altered from linear to elliptical because of the birefringent effect. Whereas,the influence of the change on the HHG in solids has not been discussed clearly.
In this paper,we measure the harmonics in a ZnO crystal as a function of the alignment of the optic axis with respect to the laser polarization.The orientation dependence of the HHG spectra is affected by the birefringence of ZnO. We find that the birefringent effect can be described by a Jones matrix even in the intense field. We introduce the Jones calculus to correct the laser polarization. We obtain the orientation-dependent harmonics with linear polarized laser pulses at the last layers of the ZnO crystal. There are distinctions between the harmonics with polarization corrections and the signals without the corrections.
2. Experimental setup
In our experiment,we use a transmission geometry. The sample is a 500-μm-thick a-cut ZnO crystal. Its roughness is less than 5 ˚A, and the purity is more than 99.99%.The transmission spectra and x-ray diffraction data refer to Refs.[38,39].The mid-IR pulse(center wavelength of 2.4 μm,temporal duration of 150 fs)is produced by a commercial optical parametric amplifier (OPA, Light Conversion TOPASprime)pumped by an amplified Ti:sapphire laser system(Legend Elite Duo,Coherent,Inc.). The repetition rate is 1 kHz.
The laser pulse is focused into the crystal at a normal incidence with a lens of 50-mm focal length.The spot size is about 150 μm in vacuum, which is measured by a knife-edge scan.To control the alignment with respect to the laser polarization and the field strength, we mount the crystal to allow rotation about its normal and translation through the laser focus. We use a half-wave plate(HWP)and a quarter-wave plate(QWP),which are set in front of the focusing lens,to control the polarization of the incident laser pulse.At the exit of the crystal,we use a combination of a polarizer(WP25M-UB,Thorlabs)and a power meter to analyse the polarization of the emitted laser pulse. HHG signals are collimated by a 50-mm-focal-length lens and focused by a lens with the same focal length. Then the signals are collected to a spectrometer with a 150 g·mm-1grating and detected by an intensified charge-coupled device camera(ICCD,PI-MAX1024UV).
3. Results and discussion
The schematic of the ZnO crystal is shown in Fig. 1(a).The blue shaded region shows the a-cut plane. The laser polarization,shown as a black arrow,is lying in this plane.θindicates the angle between the optic axis and the laser polarization.As shown in Fig.1(b),the measured spectrum covers harmonics from 4th to 9th order.The conversion efficiency of harmonics is estimated to be from 2.5×10-5(4th)to 1.0×10-7(9th). The HHG spectra are measured as a function ofθ. The wavelength of the laser field is centered at 2.4 μm and the strength is about 0.9 TW/cm2. Under this field strength, we observe the maximum yield of HHG without optical damage.The even harmonics are at their maxima when the laser polarization is along 0°or 180°, which correspond to the optic axis. And they are at their minima when the laser polarization is along 90°. The periodicity of even harmonics isπ. In addition,secondary peaks appear near 60°and 120°for the even harmonics. The odd harmonics show their maxima when the laser polarization is along 0°, 90°, and 180°. The periodicity of odd harmonics isπ/2.
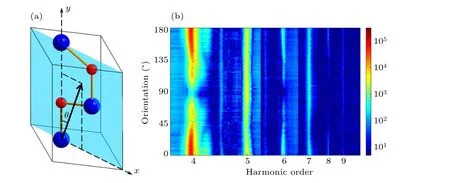
Fig.1. (a)Schematic of the wurtzite ZnO crystal with shaded region showing an a-cut plane. The Zn is shown in blue and slightly larger than the red O.The laser polarization is shown as the black arrow,and the angle θ,between the optic axis and the laser polarization is indicated. (b)High-order harmonic spectra as a function of the crystallographic orientation with respect to the polarization of the laser pulse. The crystal is rotated about the laser propagation axis to vary the angle between the laser polarization and the optic axis. The field is centered at 2.4 μm,and the strength is about 0.9 TW/cm2. The intensity of harmonics is normalized in arb. units. The periodicity of odd harmonics is π/2, and the periodicity of even harmonics is π.


whereEis the electric field of the incident laser pulse. Then we model the birefringent effect of ZnO crystal as a matrix,R.From Fig.2,we observe that the orientation of the major axis of the transmitted laser pulse is the same as that of the incident pulse. Only the ellipticity changes. So the Jones matrix can be given by
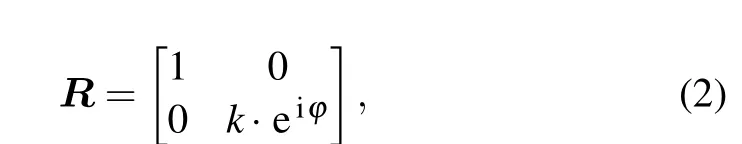
wherekis the coefficient of the amplitude of the electric field,andφis the phase difference betweenx-component andycomponent of the electric field. The transmitted pulse after propagation in the crystal is given as following:

By fitting the value ofJemittedto the experiment, we get the value ofR,which is given by
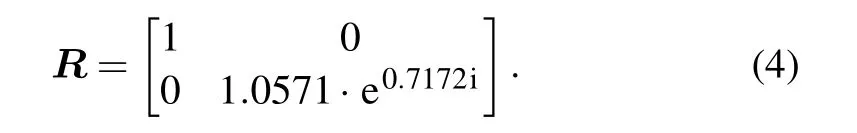
The fitting results are shown as the blue dash lines in Fig. 2.They are in good agreement with the experimental data(shown as the red solid lines in Fig.2). The agreement confirms that it is reasonable to use the Jones matrix to describe the birefringent effect of ZnO crystal even in the intense laser field.

Fig.2.Polarization of the laser pulse after passing through the ZnO crystal in the experiment(red solid lines)and the Jones calculus calculations(blue dash lines).The title is the angle between the polarization of the incident laser with the optic axis of the crystal.The intensity is normalized by the maximum. The ellipticity of the emitted laser changes from 0.05(linear,0° or 90°)to 0.38(elliptical,45°).

Fig. 3. High-order harmonic spectra as a function of the alignment of the crystal with respect to the polarization of the laser pulse by counteracting the birefringent effect. The wavelength and field strength of the laser pulse are same as those in Fig.1.The periodicity of odd harmonics and even harmonics is π/2 and π,respectively.
Then we use the inverse matrix,R-1, to counteract the birefringent effect. We firstly calculate the polarization of the incident laser pulse byJincident=R-1·Jemitted.By controlling the angles of the HWP and QWP in front of the focusing lens,we alter the polarization of the incident laser to make sure that the transmitted laser is linearly polarized along a specific direction. Then we measure the orientation dependence of the HHG using the corrected polarization laser pulses. The measurement results are shown in Fig.3. The wavelength and the field strength of the laser pulse are the same as those in Fig.1.One can clearly see some distinctions compared with the HHG spectra in Fig.1.
To show the distinction clearly, we compare the HHG with polarization corrections to the signal without corrections in Fig. 4. The blue dots are the HHG signal with the birefringent effect, and the red dots are the HHG with polarization corrections. By comparing to the even harmonics without polarization corrections, the modulation of the even harmonics from 45°to 135°is much smaller after the polarization correction. Moreover, the secondary peaks of even harmonics disappear after the polarization correction. It shows that the secondary peaks originate from the change of the laser polarization. For the odd harmonics,the intensity with polarization corrections exhibits a deeper modulation compared to that without polarization correction. The ratio between the minimum and the maximum of the 5th-order harmonic is about 0.32 (0.38 for the 7th-order harmonic, 0.5 for the 9th-order harmonic)without polarization correction. The ratio becomes about 0.1 for the 5-th order harmonics(0.15 for the 7th-order harmonic, 0.25 for the 9th-order harmonic) with polarization correction. Furthermore,the birefringence affects the symmetry of the HHG signal. As shown in Fig. 4, the symmetry axis is at 90°. The symmetry of the HHG with polarization corrections is excellent. But for the HHG without the corrections, the intensity alongθ(from 0°to 90°) is smaller than that along 180°-θ. These comparisons show that the secondary peaks,the small modulation,and the asymmetry of the HHG are associated with the birefringent effect. Some extra features are coupled in the orientation dependence of the HHG without polarization correction. It will affect the understanding of the generation mechanism of the HHG. Moreover, we need to eliminate the birefringent effect to obtain the original signals and retrieve the solid structure.
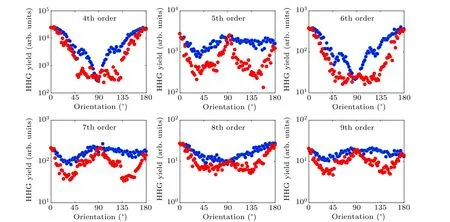
Fig. 4. Comparison of the HHG spectra from transmission through the bulk ZnO and that with polarization corrections by using the Jones calculus. The blue dots are the measurements with the birefringent effect, and the red dots are the HHG spectra counteracting the effect by using the Jones calculus.
4. Conclusion
We report the HHG spectra in ZnO as a function of the alignment angle between the laser polarization and the optic axis. The harmonics are affected by the birefringent effect of the crystal. By introducing the Jones calculus, we counteract the birefringent effect and obtain the HHG spectra with polarization corrections. There is explicit distinction in the HHG spectra compared with the uncorrected signals. Without the birefringent effect,the modulation of the odd harmonics is deeper and the even harmonics have no secondary peaks. It is important to eliminate the birefringent effect from the HHG to reflect the original structure of solid.
- Chinese Physics B的其它文章
- Numerical simulations of partial elements excitation for hemispherical high-intensity focused ultrasound phased transducer*
- Magnetic-resonance image segmentation based on improved variable weight multi-resolution Markov random field in undecimated complex wavelet domain*
- Structure-based simulations complemented by conventional all-atom simulations to provide new insights into the folding dynamics of human telomeric G-quadruplex*
- Dual-wavelength ultraviolet photodetector based on vertical(Al,Ga)N nanowires and graphene*
- Phase-and spin-dependent manipulation of leakage of Majorana mode into double quantum dot*
- Deep-ultraviolet and visible dual-band photodetectors by integrating Chlorin e6 with Ga2O3

