Simulation and experiment of the cooling effect of trapped ion by pulsed laser*

Chang-Da-Ren Fang(方长达人) Yao Huang(黄垚) Hua Guan(管桦)Yuan Qian(钱源) and Ke-Lin Gao(高克林)

1State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China

2Key Laboratory of Atomic Frequency Standards,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China

3School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100049,China

Keywords: doppler cooling,pulsed laser cooling,molecular dynamics simulation

1. Introduction

In the past two decades, optical clock technology has been developed rapidly and has currently become the frequency standard with the best accuracy and stability, and it has many potential applications in timing,precision measurement physics, verification of fundamental physical theories,detection of dark matter and gravitational waves, etc.[1-9]At the same time,new candidate systems for optical clocks have been proposed, such as highly charged-ion-based(HCI)optical clocks, and nuclear-based optical clocks.[10-12]The reference transitions for these above-mentioned clocks are insensitive to the external field, thus these clocks are considered to be one of the next-generation optical clocks with higher precision. However,for the above-mentioned clock candidates,the wavelengths of the cooling lasers are often in the deep ultraviolet (DUV) range. Though with the development of DUV laser technology, lasers with wavelengths in the order of tens of nanometers have been made,[13-16]no CW laser with wavelength less than 170 nm has been reported yet. At present,for a reference system with a cooling laser wavelength less than 170 nm, such as27Al+ion optical clock[17]and HCI optical clock,[10,11]sympathetic cooling method is required,and the state readout for the optical clock is realized indirectly with the quantum logic measurement scheme,[18]which requires complicate cooling processes such as sideband cooling,which could increase the technical complexity of optical clock implementation, meanwhile, additional uncertainty would be brought in by this scheme due to the existence of sympatheticcooling ions.[19]If DUV pulsed laser can be used for cooling these ions directly,the uncertainties of these optical clocks will be expected to be even smaller.

The following key parameters that should be considered when studying whether DUV pulsed laser can be used to cool ions are: the pulse width, duty ratio, and the linewidth of the pulsed laser, the heating rate of the ion trap, etc. Taking the27Al+clock as an example,the required cooling laser wavelength is 167 nm;while a 167 nm DUV pulsed laser had been made by Technical Institute of Physics and Chemistry,CAS, thanks to the development of deep-ultraviolet diode laser-pumped solid-state lasers(DUV-DPL).The pulse width is 200 μs with a duty ratio of only 1‰ limited by technical reasons related to the crystal growth.[20,21]It can be expected that the pulsed laser Doppler cooling effect for ions with low duty cycle should be different from that by continuous laser,which makes the efficiency and effectiveness of pulsed laser cooling has become a valuable research topic.

Many research groups in the world have conducted related research on pulsed laser cooling. In 1991, Mølmer proposed to utilize pulsed lasers with pulse width similar to the lifetime of upper state of the cooling cycle to cool atoms,which may lead to a temperature limitation below the Doppler cooling limit.[22]In 2006, Monroe’s group from the University of Michigan used ultrafast pulsed lasers for cooling the Cd+ion, reaching a temperature of 1 K.[23]In 2014, the National Institute of Information and Communications Technology of Japan successfully excited the1S0-1P1state transition of In+at 159 nm with vacuum DUV laser generated by highorder harmonics in the cavity,since the power is only 6.5 μW,this laser can only be used for detection but cannot achieve laser cooling.[24]In 2016, Udemet al.at Max-Planck Institute tried to use ultraviolet comb for Doppler cooling of Mg ion,[25]while the sympathetic cooling method is still needed in the cooling process due to the heating effect caused by the blue detuned“comb teeth”.In a word,pulse laser has not been used for mK level ion laser cooling in the world. What is the efficiency and effectiveness of pulse laser cooling? It is still an urgent problem to be solved.

In this paper, we have studied the efficiency and effectiveness of pulsed laser cooling in combination of simulation and experiment. First of all, in the experiment, we take the40Ca+ion as a research object,using the acousto-optic modulator (AOM) to modulate a continuous 397 nm laser for generating a parameter adjustable pulse laser. By adjusting the detuning and power, we optimize the effect of the Doppler cooling, and then measure the cooling result. In addition,we propose an optimized molecular dynamics (MD) simulation program to simulate the Doppler cooling process of in the ion trap. The simulations include the background heating process,continuous laser Doppler cooling process and pulsed laser Doppler cooling process. The results of comparison between the computer simulations and the experiments show that this MD-Simulation program is effective in weak laser intensity situation. Next, we use this MD-simulation method to analyze the possibility of pulsed laser cooling of27Al+as an example. This method can also be extended to other systems such as HCI optical clocks and nuclear optical clocks.

2. Optimized molecular dynamics simulation

The laser cooling process of the trapped ion is primarily affected by: (1) radio frequency (RF) field and axial electrostatic potential trapping force;(2)Coulomb interaction among ions;(3)laser cooling force;(4)random interaction forces between ions and the environment in an ion trap such as residual background gas in the vacuum chamber. The kinetic equation of a specific ion in the system can be expressed as[26]

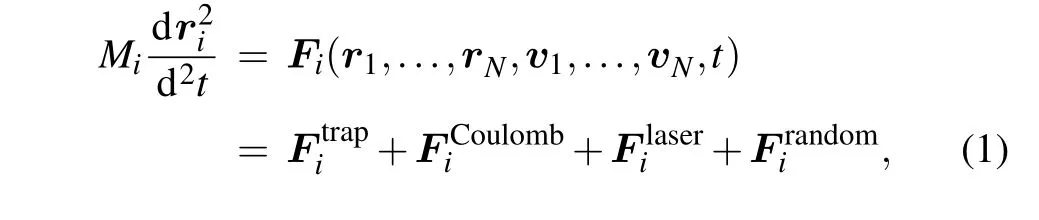
wherei=1,...,Ndenote every specific ion in a system withNions.Mi,ri,videnote the mass,position vector and velocity vector of thei-th ion,respectively.[27]

The electric potential field force applied on thei-th ion can be obtained as follows:

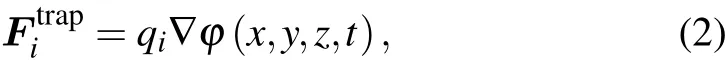
whereqiis the charge of thei-th ion,and the expression of the trapped potential field is

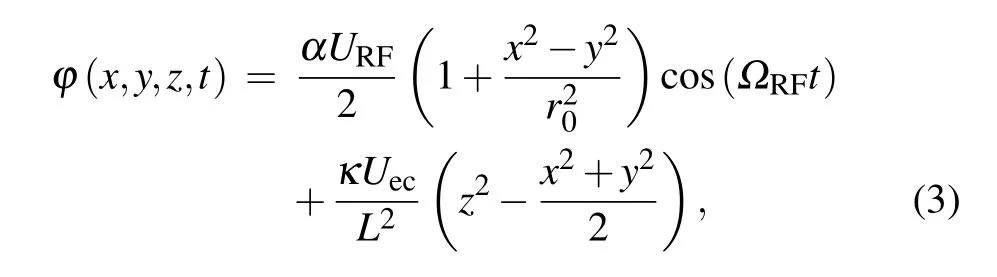
whereαandκare the radial and axial geometry factors, respectively,which are introduced because the electrodes are not perfect parabola and will be shielded by other electrodes.URFis the RF field voltage amplitude,ΩRFis the RF field angular frequency,Uecis the cap voltage,r0is the distance between the tip of the blade and the axis of the trap, andLis the tip distance between the two caps.

The Coulomb interaction force experienced by thei-th ion can be obtained by superimposing the Coulomb force exerting on thei-th ion by all other ions,which can be expressed as

whererjiis the position vector of thei-th ion relative to thej-th ion,andε0is the vacuum permittivity.

The force applied on the ion induced by the laser field can be expressed as[28]

wherevis the velocity vector of the ion,Γis the natural line width,δis the detuning of the laser, andkis the wave vector of the laser. The parameters=(Ω2Rabi/2)/(Δω2+Γ2/4)is the saturation parameter, in whichΩRabiis the Rabi frequency,s0=2Ω2Rabi/Γ2=I/Isatwhen Δω=0,in whichIsat=2π2ħcΓ/3λ3Laseris the saturation laser power intensity.[28]

The laser force of low temperature ions can be approximated with low order expression aroundv=0:F=F0-β ·v+o(v2), whereF0= (ħks/2)/[1+s+4(δ/Γ)2] can be interpreted as the average radiation pressure applied on the ion, while the effect ofFcooling=-β·vdepends on the coefficientβ=-4ħk2sδ/[Γ ·(1+s+4δ2/Γ2)2]. When the laser is red detuned, which means the detuningδ ＜0, theFcooling=-β·vis opposite to the ion’s velocity all the time like a damping force, which decelerates the ion. On the contrary,when the detuningδ ＞0,the damping coefficientβ ＜0,which leads to a heating force.

When the ion temperature is high, the high-order effect of the laser on ion cannot be ignored, so we take the original expression (5) into the simulation. On the other hand, we use the formulaFL-random=rrandom·(ħkΓ s)/2(1+s+4(δ-k·v)2/Γ2) to express the force induced by the spontaneous emission,which was often ignored in previous MD-simulation programs,whererrandomdenotes a random direction of the spontaneous emission.

Due to the non-ideal characteristics of the experimental environment such as the effect of the background gas, the limited machine precision of the trap, the electric noise on the RF voltage, we can ignore the effect of random background heating. We assume that the random background heating forceFrandomis isotropic,which obeys a normal distributionN(0,2mP/Δt),wheremis the ion mass,Pis the heating rate of the trap measured in the experiment. The motion of the ion under the action of this random force behaves as Brownian random walk stochastic process in its momentum space,which leads to a heating effect. Using the relevant conclusions of Brownian motion and the relation between the chi-square distribution and the normal distribution,we can obtain

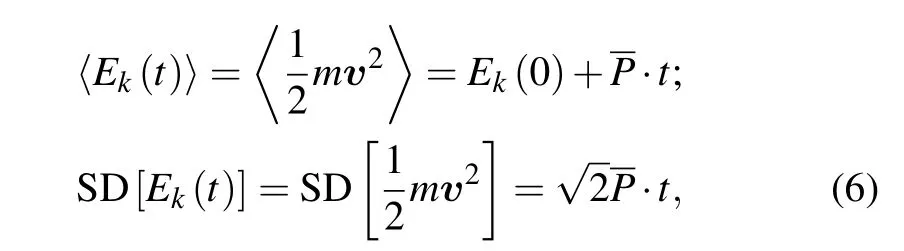
where〈···〉indicates carrying out the expectation value of the variables in brackets, SD[···] represents the standard deviation of the variables in the brackets. Formulas (6) imply that the mean(expected)value and standard deviation of the total kinetic energy of the particle increase linearly with time,under the action of the assumed forceFrandom.

Finally,we introduce time-dependent laser force to simulate the action process of pulsed laser on ions and use leap-frog algorithm[29-31]to simulate the dynamic process of the ions.

3. Experiment for the Doppler cooling of 40Ca+with pulsed laser

We chose40Ca+ion as the research object in the experiment. Due to the lack of pulse laser,we used an acousto-optic modulator to switch continuous laser to produce pulsed laser,using time sequence we could control and adjust the pulse width and duty ratio of the pulsed laser. A slightly modified new type of trap, which was first designed by NIST,[32]was used in this experiment. This ion trap has a low heating rate,which is conducive to long-term stable ion trapping, and the cooling effect may also reach a lower level.

The evaluation of ion temperature can be realized by observing the Rabi oscillation spectrum of the clock transition. The Rabi oscillation of the transition is weakly modulated by the ion temperature(phonon number)in the following form:[33]

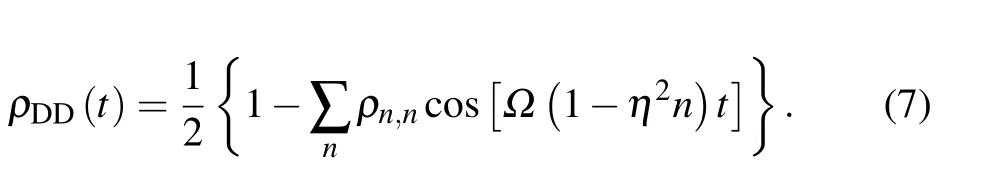
As in the case of40Ca+,tis the action time of the 729 nm laser andρDDis the population of state 32D5/2,the sum here iterates over all the positive integers,i.e.,the phonon number is 1～∞,whileρn,nindicates the population when phonon number isn.Finally,the average phonon number can be obtained by carrying out the statistical average of phonon numbern,whereηis the Lamb-Dicke parameter. Since the Lamb-Dicke parameter is less than 0.1 at most of the time,it is reasonable to expand the expression of Rabi frequency to first order inη2, which leads to an approximate analytical formula:[33]wherenis the average phonon number,andx= ¯n/(¯n+1).

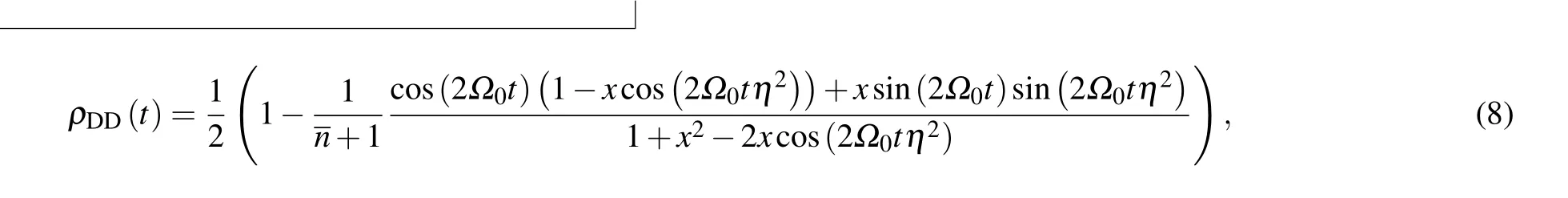
By fitting the curve data obtained in the experiment using formula(8),average phonon numberncan be obtained,while the temperature of the ion and ¯ncan be expressed as

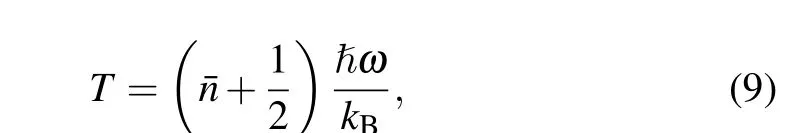
whereωis the secular motion frequency of interest,andkBis the Boltzmann constant.

3.1. Heating rate measurement

The experiment can be divided into three main parts,and the sequence is shown in Fig.1:

In the first part, we adopt a fixed near red detuned frequency for the 397 nm laser to cool the40Ca+for 2000 μs.The purpose is to make each experiment starts at the identical low initial temperature(close to the Doppler cooling limit). In the second part,we turn off all the lasers and let the40Ca+be heated for a while. This allows the temperature of the40Ca+to rise for the measurement in the third stage. In the third part, we use a 729 nm clock transition laser for probing the40Ca+. After that,a 397 nm laser is used to observe the fluorescence signal of the ion,for counting the population between the states of 42D1/2and 32D5/2, we take 75 measurements at each experimental point to get the average result. By obtaining the relation between the population and the action time of 729 nm laser, we constructed a Rabi oscillation curve to be fitted to get the temperature at each time. Finally, we got the relation between the temperature and the waiting time,i.e.,the heating time,which indicates the heating rate of the trap.

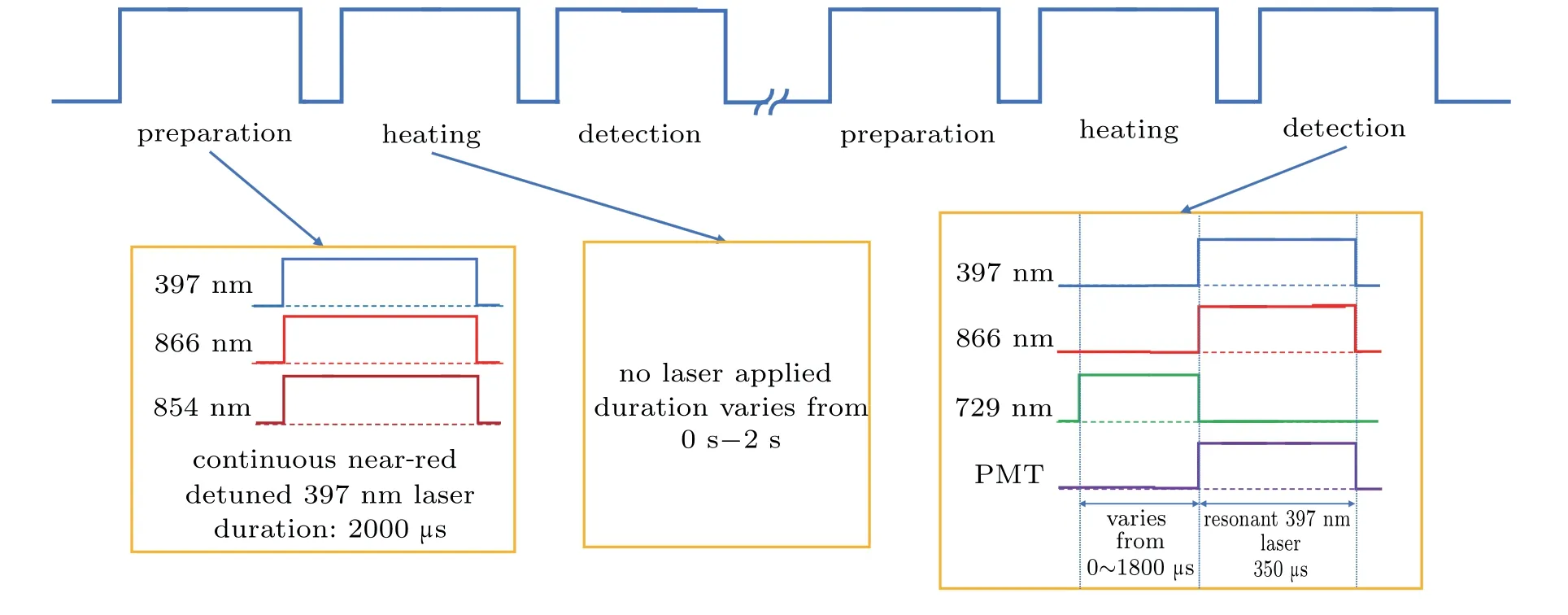
Fig.1. Schematic for the pulse sequence in the heating rate measurement.

3.2. Doppler cooling of the 40Ca+with pulsed laser

We measured the influence of two important parameters in the experiment, which are the laser’s effective pulse width and the duty ratio of the pulsed laser. The experiment can be divided into three main parts, and the sequence is shown in Fig.2.

In the first part, we used a fixed-frequency red detuning laser to cool the40Ca+. The purpose is to make the40Ca+at the same initial temperature at the beginning of each experiment,so that we can ensure that each experiment is carried out under the same initial conditions. The reason for using far-red detuned laser is to keep the40Ca+at a high initial temperature for the next cooling process experiment. In the second part,we used a 397 nm pulsed laser for cooling; the pulse width,pulse number,and the duty ratio parameters of the laser were continually changed during the experiment. In the final stage,the same as the previous experiment, by detecting and fitting the Rabi oscillation diagram we obtained the ion temperature.Based on this, we can give the diagram that the temperature of40Ca+ion changes with time under the action of 397 nm pulsed laser with given intensity,given red-detuning and given pulse on/off time parameters.

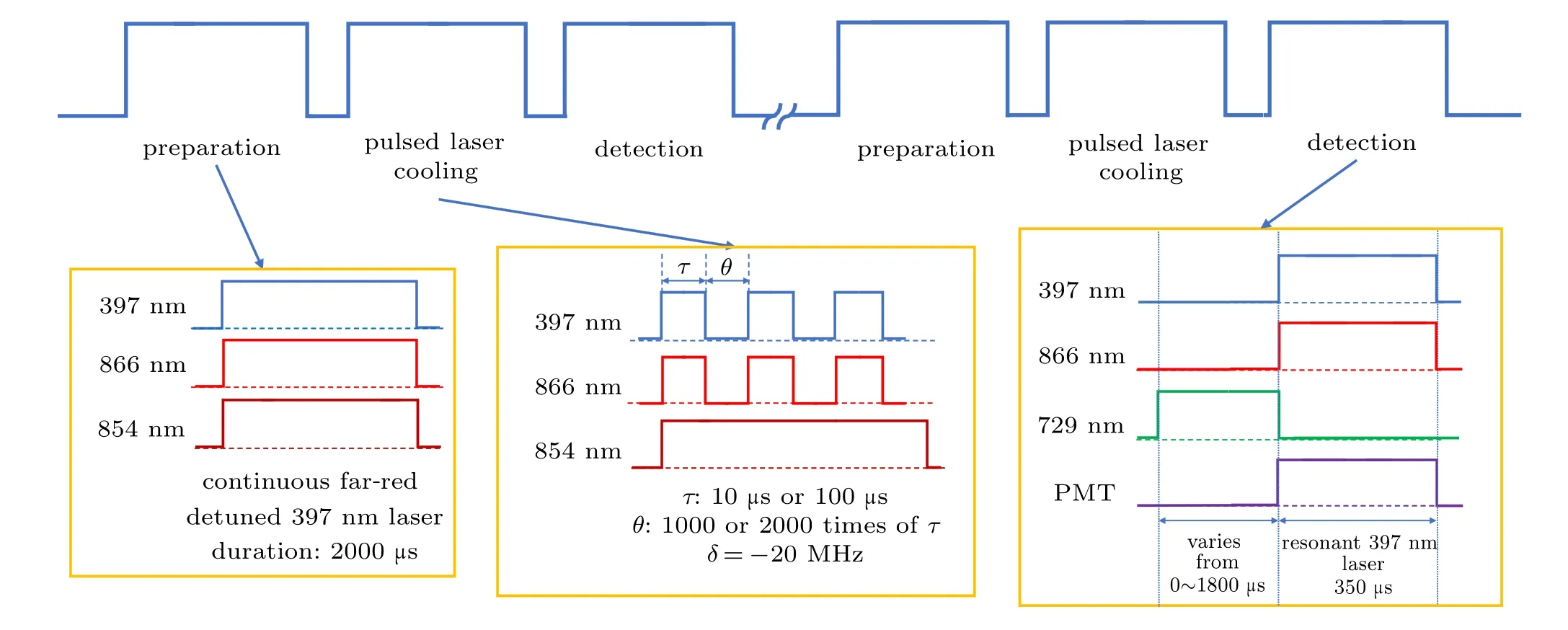
Fig.2. Schematic for the ion temperature measurement after the laser cooling.

4. Analysis

By substituting the relevant parameters in the MDsimulation program with the measured heating rates,the pulse width and duty ratio used in the experiment,we performed the simulation. After obtaining the data derived from the MDsimulation, we put the experimental and simulation results in the same graph for comparison and analysis, as shown in Figs.3 and 4.

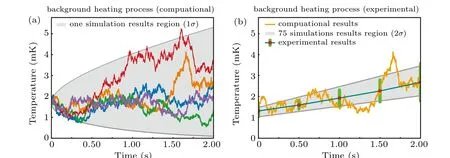
Fig. 3. (a) The heating process calculated by MD-Simulation. Each color line is one specific simulation result, since all the processes are stochastic,actually there are countless possible results,we present 5 results here in the figure without loss of generality,in the same situation of Figs.4 and 5. The gray area indicates one standard deviation range of the single simulation result. The blue line with green bar in(b)shows the experimental results(each measurement point is an average of 75 measurements),the orange line shows one simulation result,and the gray area shows two standard deviation ranges of the average of 75 simulations.

Fig. 4. Comparison between experiment and simulation of the Doppler cooling by pulsed laser. The results under different laser parameters are shown,in which the blue points represent the measured data,and the color curves represent the simulation results of several numerical calculations.Since the process is stochastic,there could be countless possible real processes,five possible results are shown in each picture.

It can be seen that MD-Simulation program gives a fairly consistent result in each case,some deviation of the blue dots from the simulation results could be due to the change of the experimental environment during the long period of the measuring procedure.In addition,due to the low heating rate of the ion trap used in the experiment, the on/off time of the pulsed laser does not seem to significantly affect the cooling process of40Ca+. Of course,the higher the duty ratio is,the more stable the temperature variation of the ion is,while the lower the duty ratio is,the more likely the energy of the ion will change randomly during the light-off period,and the greater the temperature variance there will be.Therefore,we can observe that when the duty cycle is 1/2000, the jitter of ion’s temperature appears to be larger than the situation when the duty cycle is 1/1000. It needs to be mentioned that due to the fact that the Doppler cooling process of40Ca+(down to the Doppler cooling limit)only requires a few hundreds of microseconds under the initial conditions we have given, the laser action time of 100 μs is enough for significantly reducing the ion’s temperature, and the horizontal axis in the figure is in the scale of seconds, which makes the deceleration process of 100 μs appear to be very steep in the figure.

Based on the above results, we believe this MDSimulation program can be reasonably applied to a wider range of situations. For example, under the condition that given the duty ratio of the pulsed laser,how much should the heating rate of the trap must be controlled so that the ion can be effectively cooled? Because it is difficult to adjust the heating rate in a large range, to explore the problem by means of MD-Simulation is an effective solution.

Next, we take the27Al+as an example, using the pulse width and duty ratio of the laser mentioned in Refs. [20,21](the pulse width of the 167 nm pulsed laser is 200 μs, and the duty ratio is 1‰)as the input value of the model,through calculation and simulation,the possibility of using this pulsed laser to achieve Doppler laser cooling of the27Al+has been explored.

Through a simple analysis of formula(6),we can see that the interaction between laser and ion is positively correlated withΓ. When the natural widthΓis large and the detuning amountδis small, the interactionFbetween laser and ion is almost proportional toΓ. Meanwhile,ΓAl+is about 10 times that ofΓCa+, which means that the interaction intensity between 167 nm laser and27Al+is almost 10 times that of 397 nm laser and40Ca+. It can be foreseeable that aluminum ions will be cooled down faster under the action of 167 nm laser, and molecular dynamics simulation does give this result. We give the temperature change of27Al+in one second under the action of 167 nm pulse laser under three different trap heating rates (the initial temperature given in this direction is about 37 mK),as shown in Fig.5.

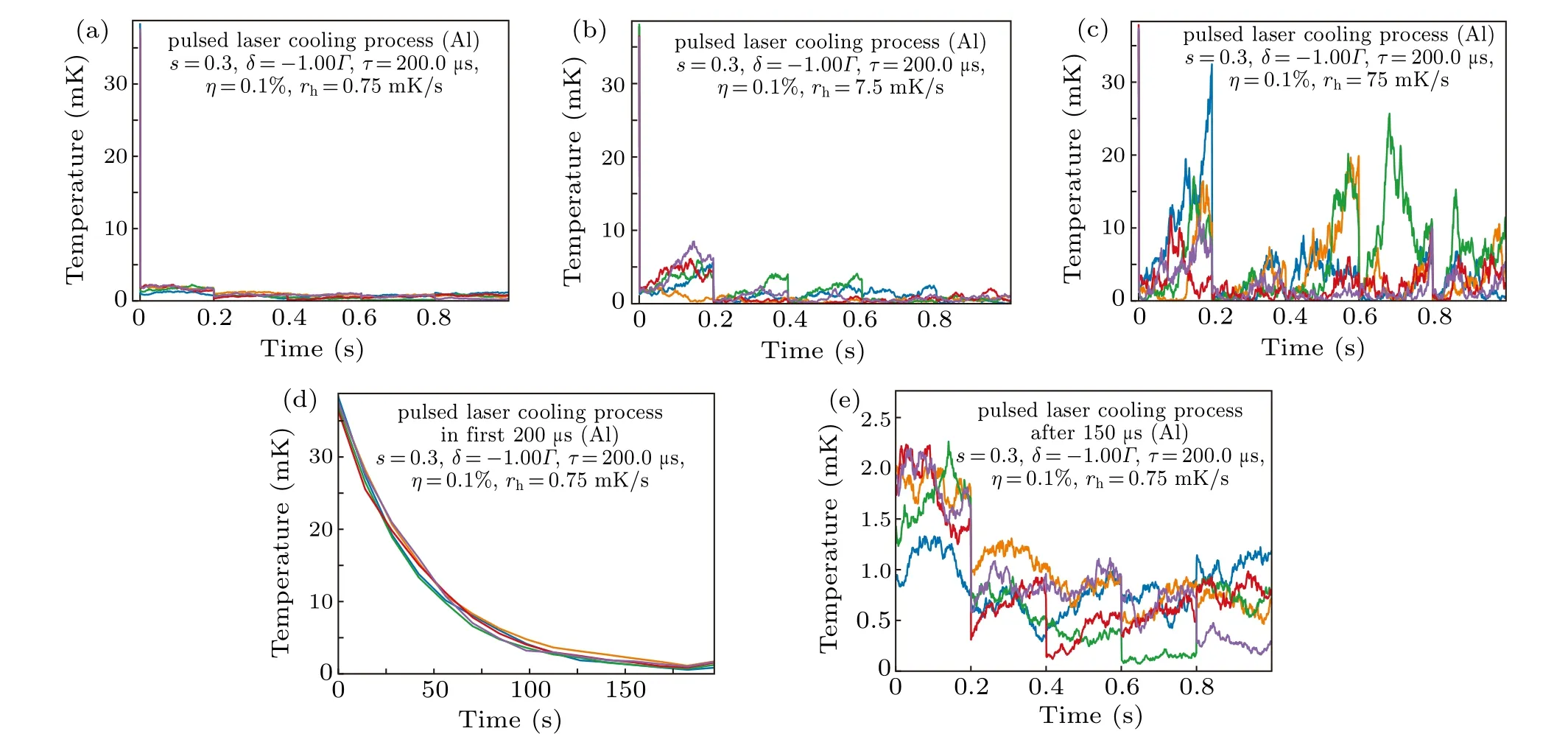
Fig.5. Simulation results of 27Al+ cooling by 167 nm pulse laser with pulse width of 200 μs and duty ratio of 1‰.Note that the deceleration effect of the 167 nm laser on 27Al+ is so strong that the 27Al+ in each group of the simulations experienced the initial rapid cooling process,which leads to the sharp drop at the beginning of the curve,as shown in(a)-(c). (d)The energy change in the first 200 μs. (e)The evolution after the first 150 μs of(a),performed under these parameters: s=0.3,δ =-1.0ΓAl+,τ =200 μs,η =0.1%and rheating =0.75 mK/s(the same phenomenon happens in (b) and (c), in which the heating rate of the trap are set to be 10 and 100 times of the original heating rate respectively with the other parameters unchanged).

From the foregoing discussion,we can see that this MDSimulation program gives a relatively consistent result with the experiment for the situation of40Ca+. On the other hand,because the laser cooling process of40Ca+and27Al+obey the same physical mechanism, the MD-Simulations of these two ions also give fairly consistent results as expected. In this sense,the simulation results given by this program for the situation of27Al+should also be able to guide relevant experiments.

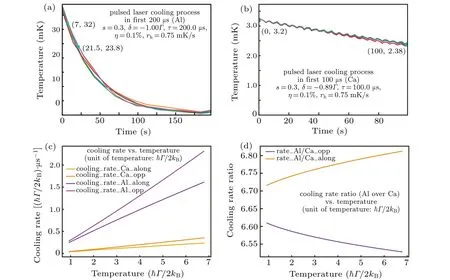
Fig.6.Comparison between27Al+and40Ca+.Figure 6(a)showsthefrist200 μs ofFig.5(a)wh〈ileF〉ig.6(b)showsthe frist100 μs ofFig.4(a).Figure6(c)shows thecooling rateof both 27Al+and 40Ca+basedonthe formula Pcooling=-βv2,whichmeans how muchthe coolingrate theionwill experiencewhenitisat certainaveragetemperature(the unitof temperature hasbeenconvertedto ħΓ/2kB,whichis the formof theDoppler cooling limit). Figure6(d)givesthe ratioof the cooling ratebetween27Al+ and 40Ca+. Thesuffxialong andopp indicatethe velocity of ion is along the laser propagation direction and opposite to the laser propagation direction,respectively.

It can be seen from Fig.5 that for ion traps with low heating rate, the pulsed laser with the parameters used above can cool27Al+to the order of mK. However, as the heating rate of the trap increases,the temperature of the ions becomes difficult to control. In order to keep the temperature fluctuation above the cooling limit within 2 mK as an example, the temperature rise of27Al+in the off-time,which is 200 ms,should not exceed 2 mK, which means that the heating rate of the trap should be controlled within 10 mK/s. Since the heating of the27Al+mainly occurs in the off-time of the pulsed laser,as long as the temperature rises within 2 mK during this period,the 167 nm cooling laser in the next 200 μs will certainly cool it to the limit cooling temperature. When the trap heating rate reaches 100 times of the original heating rate of the trap used in our experiment,the temperature of27Al+fluctuates sharply in a wide range,the27Al+ion cannot be cooled effectively.

5. Conclusion

We have explored the Doppler cooling process of the ions in the ion trap by constructing a more accurate and more suitable molecular dynamics simulation program in the case of pulsed laser cooling. Compared with the experiment, the results show that the self-built MD-Simulation program does give reasonable results. In addition, we realize that the deceleration efficiency of 167 nm laser acting on27Al+is about 6.6-7.1 times that of 397 nm laser acting on40Ca+, and that the cooling effect of 167 nm pulse laser acting on27Al+is significant in 200 μs during the on-time of the pulsed laser,which means that it is not significantly different from the situation of continuous laser. Finally,the key factor to control the temperature of ions is the heating rate of the trap. As long as the heating rate is small enough,the ion temperature can be effectively reduced and controlled. According to the simulation results, the limit value of the heating rate is given. The comparison between40Ca+and27Al+shows that it is feasible to apply this method to the guidance of the experiment on27Al+.

Acknowledgment

We thank Lijun Du,Xiaozhou Yang,and Qiongli Wu for their fruitful discussions and help.