Fast qubit initialization in a superconducting circuit*

Tianqi Huang(黄天棋), Wen Zheng(郑文), Shuqing Song(宋树清), Yuqian Dong(董煜倩), Xiaopei Yang(杨晓沛),Zhikun Han(韩志坤), Dong Lan(兰栋), and Xinsheng Tan(谭新生)

National Laboratory of Solid State Microstructures,School of Physics,Nanjing University,Nanjing 210093,China

Keywords: active reset,quantum cooling,thermal population

1. Introduction

Quantum computation calls for high fidelity operation,which requires precise state preparation.[1-3]Instead of qubit initialization by passively waiting,[4]active reset can rapidly implement the preparation of the qubit system,increasing the experiment repetition rate. Meanwhile, by eliminating residual populations in excited states, the qubit can be thermally refrigerated, thus leading to fidelity improvement and decoherence suppression. Moreover,the active reset has indispensable applications in quantum error correction code,[5]where reusable ancillary qubits are essential.

Previously, there are several routines of active reset, one is measurement-based, such as post-select[6]and herald,[7]which reveals to be non-deterministic. Moreover, readout fidelity sets the limitation to reset performance due to the back action involved in measurement. A tempting improvement is feedback,[8-10]where iterative closed-loop control is performed by injectingπpulse triggered conditioning the outcome of the consecutive measurement. However,this method carries the drawbacks like relatively long latency(several hundred nanoseconds)and requirements for high-speed digits.

Apart from the above mentioned methods, alternative approaches like frequency detuning[11-14]and microwave driving[13-18]circumvent the requirement for high fidelity measurement. A primary idea rests in the latter involves dissipative environments engineering, such as reservoirs typically cooler than superconducting qubits, Purcellfiltered resonator,[12]quantum-circuit refrigerator,[19,20]and low-quality-factor cavity.[15-18,21]Nevertheless,with ancillary circuit elements introduced, this may cause the consumption of on-chip space and complex design of processor layout.

In this paper,we demonstrate a reset protocol in the platform of superconducting quantum circuit. Initially there is residual thermal population in the excited state of a target qubit(labeled asQa). We drive the target qubit and transfer the unwanted thermal population to an ancillary qubit, which is denoted asQb. Thus, the thermal population will be relocated from the computational space to the auxiliary levels. After tuningQbto the avoid-crossing point, a SWAP operation results in the cooling effect of the qubit. We characterize our approach at different temperatures and obtain the effective temperatures from fitting Dirac-Fermi statistics, which suggests that the qubit system can be effectively cooled after reset,thus performance improvement will be expected.Comparing to the current methods, our approach is fast and easy to implement.With the further increase of the operation fidelity, this technique provides a useful tool for scalable quantum processing.

2. Experiment method

In our experiment, the sample consists of six transmons,which are in an array with nearest-neighbor coupling through static capacitor (Fig. 1(c)). Each qubit is readout with an individualλ/4 coplanar resonator which is coupled to the transmission line on the sample. The chip is mounted in a dilution refrigerator with a temperature around 30 mK.Each qubit can be drivenin situby microwave signal (XY), and biased by inserting DC currents into flux lines(Z). The reflected signals from the resonators will be transported through co-axial lines and amplified by a HEMT amplifier,finally collected by the analog-to-digital converter. Without loss of generality,we initialize the target qubit (Qa) via an ancillary qubit (Qb) to demonstrate our scheme.The system Hamiltonian can be written as

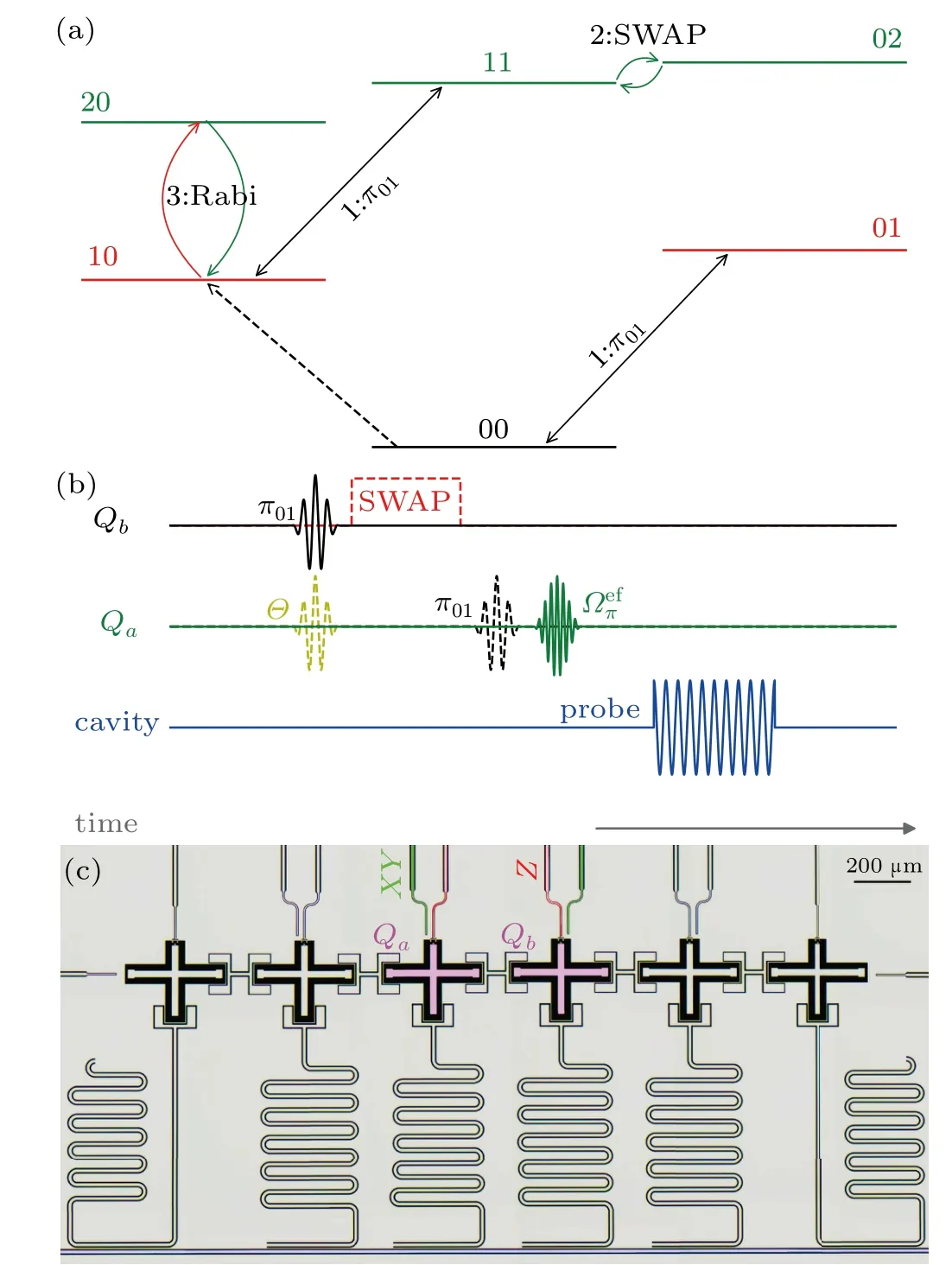
Fig. 1. (a) Diagram illustrating the principle of our protocol with Qa and Qb. Step 1, a π01 pulse corresponding to the transition frequency in the{|0b〉,|1b〉}subspace of Qb. Step 2, a tailored square pulse sented through flux bias line,whose voltage and duration are finely tuned to perform a full SWAP gate at the avoid-crossing point of |1a1b〉↔|0a2b〉. Step 3, a Rabi oscillation pulse Ω12π driving qubit evolution in {|1a〉,|2a〉} subspace, following a π pulse flipping the|0a〉and|1a〉states of Qa. (b)Pulse sequence versus time. The yellow pulse is aimed to prepare Qa to an arbitrary superposition state in the{|0a〉,|1a〉}subspace. A probe pulse is produced at the end of every round. (c)Blue(green,red,and magenta)color represents transmission line(drive line,flux line,and transmons).

Our scheme is divided into two steps, as illustrated in Fig. 1(b). First, we promote aπ01pulse toQb, in order to flip the populations between|0b〉and|1b〉states,which can be expressed as a transformation matrix ˆUbπ=∑(|ia1b〉〈ia0b|+|ia0b〉〈ia1b|). Second,a flux pulse is applied toQbto ramp it approaching the avoid-crossing point of|1a1b〉↔|0a2b〉transition,inducing vacuum-Rabi oscillations between two qubits.After fixed flux pulse duration (i.e., 27 ns), a full SWAP operation ˆUSWAP=|0a2b〉〈1a1b|+|1a1b〉〈0a2b|is conducted,resulting in population reversal between|1a1b〉and|0a2b〉.

By tracing out the degree of freedom of the ancillary qubitQb,one can obtain the state matrix of the target qubitQa. As ˆρa=(P00+P01+P10)|0a〉〈0a|+P11|1a〉〈1a|. The population in the excited state is deduced asP11. Nevertheless,this figure merely gives an optimal estimate which can hardly be reached in this experiment owing to the drawbacks in our system,and we will give an analysis latter.

Normally, we obtain the population of each energy levels from the measured amplitude of the signal, which can be written as

wherePiis the population at|i〉andαiis the ideal voltage measured when the qubit is at|i〉. Notice that normallyαiis calibrated,and we solvePifrom the equation above. However,in this experiment, we can not obtain theαidirectly, due to the noise of our instruments. Here we utilize a routine to obtainPi, in which an additional step is introduced. We drive a Rabi oscillation ofQabetween|1a〉and|2a〉states by anΩ12πpulse (green solid line). The outcome signal can be fitted to a sinusoidal envelopeA1(0)cos(θ).A0andA1correspond to different situations whetherQais prepared to|0a〉or|1a〉previously(black dash line),whose expression is given as

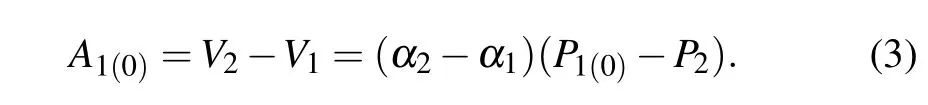
SinceP2≪P1,we can deduce the spurious excited populationsP1,as below:

3. Results and discussion

Considerring the fact that the fringe of Rabi oscillations is proportional toP1, one can characterize the residual thermal population by Rabi oscillation. We obtained that the initial equilibriumP1ofQais around 7% at 30 mK. After reset,P1achieved 2.55%. To amplify the cooling effect and investigate the efficiency changing with the temperature, we then increased the temperature of the cold plate of the dilution refrigerator. The Rabi oscillations at different temperatures (50 mK, 100 mK, 150 mK) are plotted in Fig. 2. Figure 2(a) corresponds to resetQa. Only three periods of Rabi oscillations are shown, whose amplitudes are fitted by the standard Rabi model (solid and dash lines), from which we can calculate the spurious thermal populations to be (0.1096, 0.1385, 0.1859) and (0.0309,0.0445,0.0786)before and after the reset. As the temperature rise, more quasi-particles will be invoked,[22]leading to the deterioration of remnant thermal populations. The efficiency increases. Figure 2(b) shows the outcomes related to resetQbusingQa. Similarly, the spurious thermal populations are(0.0907,0.1153,0.1655)and(0.0464,0.0688,0.1146)before and after the reset. Switching the roles of the qubits produces a variation in the reset performance, which arises from the environmental differences experienced byQaandQb. When climbing up to 150 mK,the lines become skewed owing to the reduced dephasing time.

Fig. 2. (a) Rabi oscillations of Qa at different temperatures (50 mK, 100 mK, 150 mK). X (Y) axis is the Rabi evolution time (normalized Rabi amplitude). Red(black)dots along with error bars depict results without(with)reset. Solid(dash)line is fitted to the standard Rabi model,from which we can calculate the spurious thermal populations to be (0.1096, 0.1385, 0.1859) and (0.0309, 0.0445, 0.0786) before and after the reset. (b) Reset outcomes of Qb. The spurious thermal populations are calculated to be(0.0907,0.1153,0.1655)and(0.0464,0.0688,0.1146)before and after the reset.

To characterize the efficiency for different initial states,we prepareQaat a superposition state,as shown in Fig.3(a).We demonstrate the reset efficiencyηto be (P1-P1′)/P1, a figure comparing the relative change ofP1before and after the reset,which can be referred in the inset. In the worst case,all populations are initialized in|1〉(Θ=π), the reset operation becomes equivalent to a singleπflip, thusηis almost zero.While prepared at|0〉,the efficiency is around 100%theoretically.

It is worth noting that the deviation of experiment results from theory can be primarily attributed to the limited SWAP gate fidelity,which is measured to be 98%. The distortions in flux pulses are unavoidable, owing to the limited bandwidth in digital devices and lines. Previously added flux pulses and crosstalk with other qubits also bring error. In recent publications,several groups have enhanced two-qubit gate fidelity to over 99.6%,[2,23]which opens up an opportunity to display the advantage of our method by carrying out a high fidelity SWAP gate. We investigate that through perfect pulse parameters,the reset performance can be improved substantially,by eliminating the thermal population to less than 1%, thus fulfilling the request for error correction.

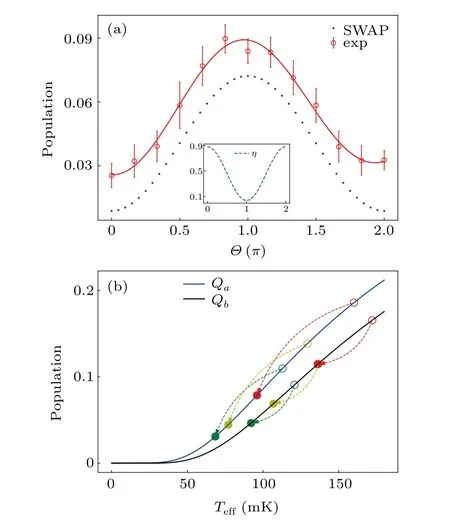
Fig. 3. (a) The chart illustrates the reset results for Qa from arbitrary superposition states at 30 mK (red dots along with error bars displaying the standard deviations). The horizontal axis corresponds to evolve along the longitude of the Bloch sphere for one period.The solid line is fitted to a Rabi model. A minimum P1 reads 2.55%at Θ =0,representing the residual thermal population after reset. The dot lines are the simulated results using the Qutip package. The inset gives an example of reset efficiency η. When the qubit is initialized to|0〉(|1〉),η reaches the maximum(minimum). (b)Using the statistics from Fig. 2, one can calculate the effective temperatures of the qubit with Dirac-Fermi distribution. Teff differs a bit for Qa and Qb,due to the different environments experienced by the qubits. Here,different colors (green, yellow, red) correspond to temperatures at 50 mK, 100 mK,150 mK,respectively.

From another perspective of view, we further derive the effective temperaturesTeffof the qubits using the statistics from Fig.2 according to Dirac-Fermi distribution(Fig.3(b)).Due to the difference in the environments experienced by the qubits,Teffdiffers a bit forQaandQb.Specifically,at different temperatures (50 mK, 100 mK, 150 mK),Qais cooled from(112.83 mK,129.31 mK,160.04 mK)to(68.5 mK,77.07 mK,96.02 mK),andQbfrom(120.75 mK,136.60 mK,172.05 mK)to(92.08 mK,106.84 mK,136.1 mK).

4. Conclusion

We propose and realize an active reset protocol in cQED,showing a potential to eliminate residual thermal population in 27 ns,which is faster than the results reported before. This scheme calls for neither feedback nor dissipative environment,only a spare qubit is required. Besides,it is general and can be easily transported to other architectures, like trapped-ion,[24]NV-center,[25]quantum dots,[26]etc.Since amplifying the signal strength can significantly improve the accuracy and speed of state discrimination,one can further improve the efficiency of reset by using a JPA to readout the qubit.