基于流固耦合计算的边坡在水位变动情况下的变形机理分析

崔高麓

(常州市武进水利工程有限公司，江苏 常州 213000)

1 概 述

在水利水电工程的修建、运营过程中，不可避免地会遇到一些不稳定的库岸边坡，因此对不稳定斜坡的变形机制进行研究具有十分重要的意义[1-6]。目前，国内外学者对此已经进行了很多研究[7-10]。

本文阐述了水库水位升降对边坡的影响规律，并探讨了一种进行流固耦合计算的方法。在这种方法的基础上，选取3类典型边坡进行数值计算，以期计算结果为类似工程提供借鉴与参考。

2 边坡响应特征定性分析

对水库边坡而言，除降雨、地震、人类活动扰动之外，水位升降往往是最重要的致灾因子。水位活动对边坡稳定性造成扰动，从整体上的影响来看，水位上升、下降过程导致边坡浸润线的空间几何分布出现重分布。对给定的边坡而言，升水位后将会导致边坡浸润线上升，浸润线变化范围内的岩土体重度将会由半饱和/全饱和容重逐渐转变为天然容重。在这个过程中，这一部分岩土体重度将会变低。除此之外，还会导致这部分的应力路径发生变化，抗剪强度参数也会出现变化，由相对低值逐渐升高。在这个过程中，将会导致浸润线两侧岩土体受重力作用下的应力环境发现显著变化，最直接的后果就是临界线上下两侧岩土体的位移量值不同。若岩土体水理性较好，那么剪应力集中的情况不会太严重；但若是页岩、泥岩、黏土或是含蒙脱石较高的岩石，在前缘有临空条件的情况下，极有可能出现滑动，甚至出现滑坡。如意大利的瓦伊昂大坝，当初选址就是因为没有考虑软弱夹层的工程物理特性，最后导致灾难性的后果。从局部影响来看，水位升降过程将会导致边坡坡脚的岩土体应力环境出现明显变化，若坡脚为边坡的锁固段，那么在浸润过程中，坡脚变软，整体稳定性将无可避免地降低。另一方面，若坡脚为下滑段(这种情况往往比较少见)，那么浸润过程将直接劣化坡体的应力环境，导致其更容易出现滑动。以上分析主要还是从定性的角度进行介绍，要佐证笔者的论述，需要进行数值计算。

3 多场耦合的数值计算前处理

3.1 计算模型设计

要进行合理的多场耦合计算，首先需要建立合理的数值计算模型。建立数值模型时，根据场地的地形特征，选取合理的地层剖面，具有以下几点特征：①能准确反映斜坡结构特征；②剖面方向能代表潜在主要滑动方向或是坡向；③尽可能全面展示场地的地质要素(如挖方路基、填方路基、沟壑、拉陷槽、裂缝等)。

选取合理的地层剖面后，对不同区域赋予不同的材料模型。堆积体、基岩采用弹塑性模型。如有工程措施，则结合实际情况讨论。如锚索、土钉等一般采用结构杆单元表示，抗滑桩、护面墙一般采用结构梁表示。材料选取正确后，再给相应的区域赋予不同的参数值。然后结合现场的结合尺寸比例进行网格绘制(一般采用1∶1，或者1∶200、1∶500、1∶1 000缩放)。网格形状方面，一般采用四边形较好，但是局部几何空间不满足的情况，最好采用三角形单元嵌入，总之尽可能采用“总体四边形单元，局部三角形单元”这种网格划分模式。完成网格绘制后，需要施加边界条件，此处主要根据现场实际情况来确定(一般左右两侧三向约束，底面三向约束)，此处不再赘述。完成以上工作后，需要考虑渗流场的分布情况，需要提前绘制初始水位线，坡体两侧施加水头边界，在给定的渗透曲线的前提下，采用半饱和/饱和有限元计算，检查计算结果生成的水位线。若浸润线与现场实测线吻合，则可以继续计算；若否，则返回检查模型的合理性。

按照本原则，对选取反倾变质岩边坡、上硬下软型边坡、顺倾边坡建立数值计算模型，见图1-图3。

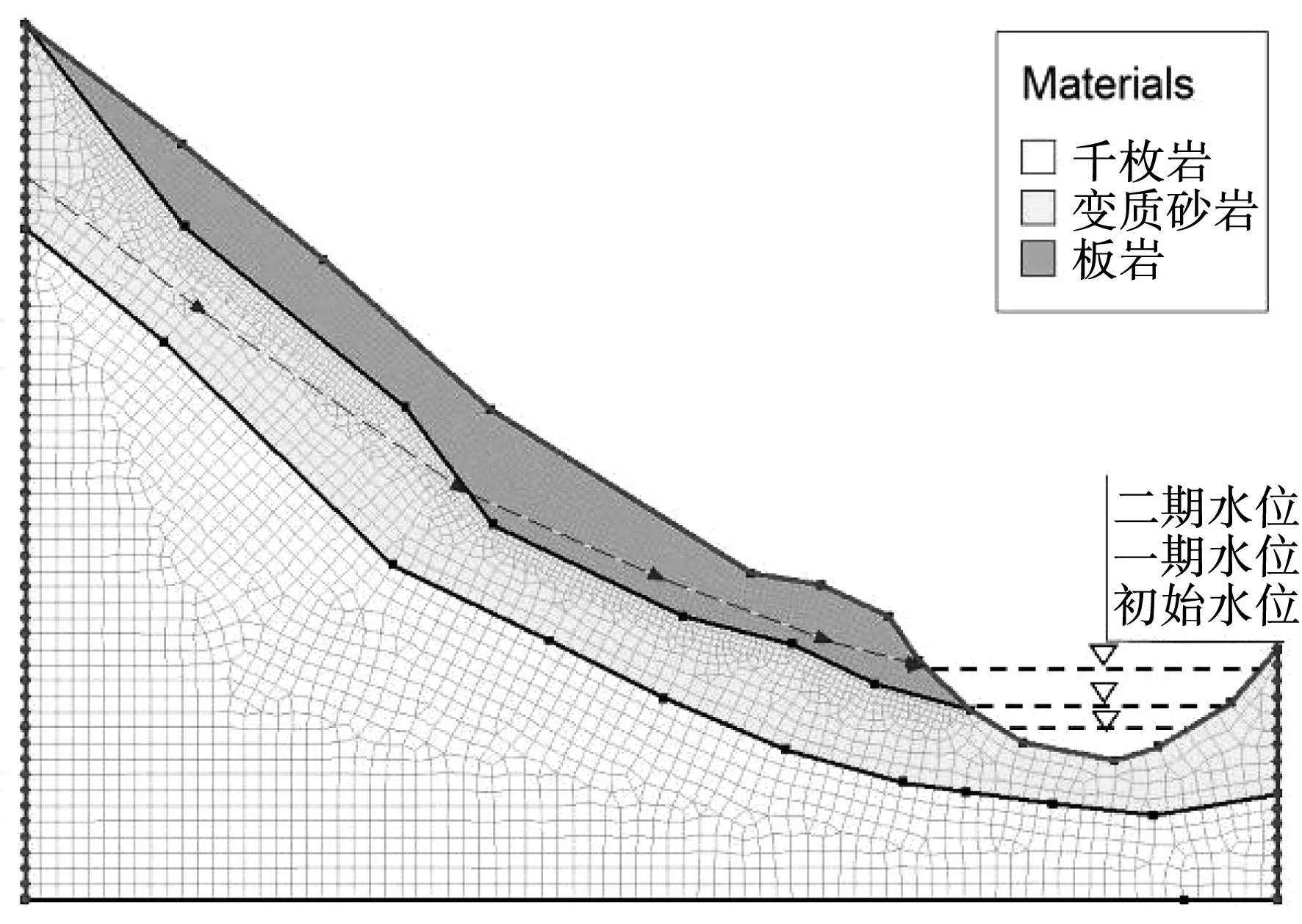
图1 反倾变质岩边坡数值计算模型

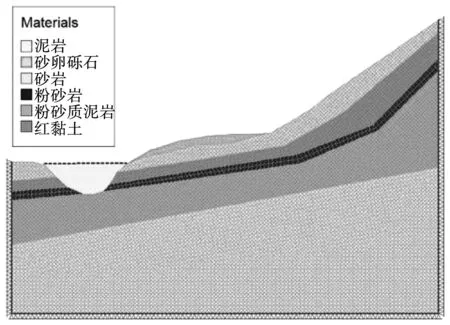
图2 上硬下软型岩质库岸边坡数值计算模型

图3 顺层岩质边坡

3.2 工况与模拟方案标定

本次数值计算主要考虑以下3种工况，即①工况一：蓄水(仅考虑自重，g=9.8 m/s2)；②工况二：蓄水；③工况三：泄水。

具体模拟方案如下：

1) 工况一将有限元软件中的SWEEP/W和SIGMA/W模块相结合，按实际情况绘制水位线，两侧边界设置水头，材料渗透系数利用Van Genuchten估计方法，结合体积含水量反推渗透系数，在渗流场计算结果的基础上，引入应力、应变分析模块，对边坡的响应特征进行分析。

2) 工况二：完成初步分析后，按照实际蓄水位添加水头，进行应力重分布分析。

3) 工况三：结合实际泄水位进行水头设置，然后进行荷载变形分析。

4 案例分析计算

4.1 反倾变质岩边坡流固耦合特征分析

在3种工况下的计算结果见图4-图7。

图4 常水位最小总应力

图5 常水位最大剪应变

图6 蓄水工况最小总应力

图7 蓄水工况最大剪应变

由图4-图7可知，在蓄水作用下，最小总应力呈条状分布，随着深度的增加而增加，压应力主要以重力场为主，最小总应力负值(拉应力区)主要出现在坡表，应力集中以陡缓交界处最为明显，拉应力最大值约80 kPa。最大剪应变方面，与常水位相比，有增加的趋势，最大达到0.064。根据以上分析，认为水库蓄水后，导致边坡出现变形，整体处于不稳定状态，需要采取治理工程措施。

4.2 上硬下软型岩质库岸边坡流固耦合特征分析

这类边坡在3种工况下的计算结果见图8-图13。

图8 常水位最小总应力云图

图9 常水位最大剪应变云图

图10 蓄水工况最小总应力

图11 蓄水工况最大剪应变

图12 泄水工况最小总应力

图13 泄水工况最大剪应变

根据以上计算结果可知，坡体处于常水位时，最小总应力总体受压应力控制，坡表局部位置和坡体内部局部出现拉应力单元，说明整体稳定性较好，但可能存在局部稳定性问题。相比天然工况，蓄水后，最小总应力的拉应力区明显扩展，沿坡体内部逐渐延伸至斜坡前缘。最大剪应变方面，应变增量与屈服单元沿软弱层发育，说明对这类上硬下软型边坡来说，在库水作用下，应注意极软层前缘临空情况，一旦蓄水，该层极有可能发育为相对不稳定层。在泄水工况下，斜坡中上部坡表拉应力区贯通，但斜坡中下部拉应力区未贯通，软弱层内部出现剪应变集中，但量值相比蓄水工况更小，说明对上硬下软型边坡来说，稳定性受蓄水影响更大。

4.3 顺层岩质边坡流固耦合特征分析

这类边坡在3种工况下的计算结果见图14-图19。

图14 天然工况最小总应力云图

图15 天然工况最大剪应变云图

图16 蓄水工况最小总应力

图17 蓄水工况最大剪应变

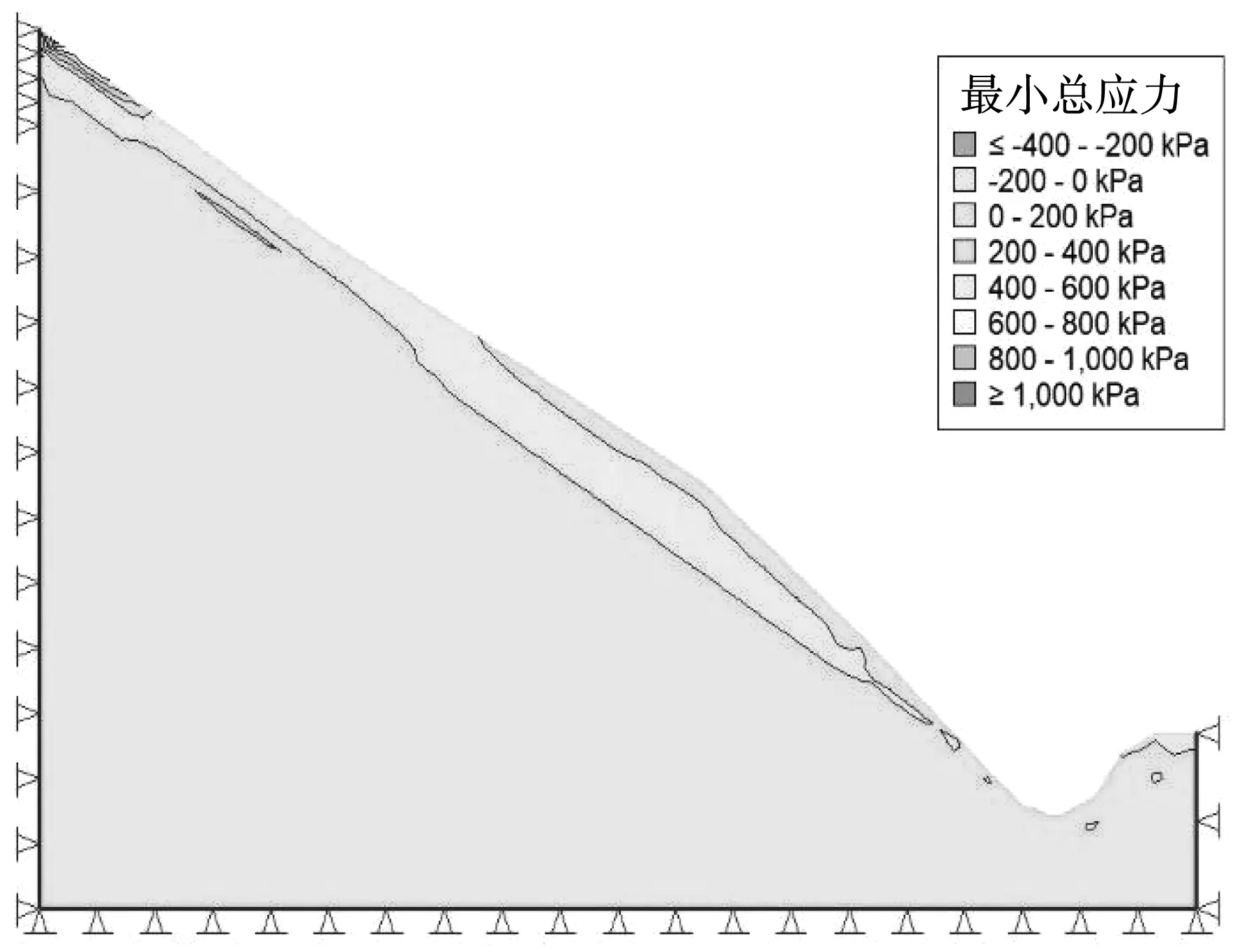
图18 泄水工况最小总应力

图19 泄水工况最大剪应变

计算结果显示，坡体处于常水位时，最小总应力总体受压应力控制，坡表局部位置和坡体内部局部出现拉应力单元，说明整体稳定性较好，但可能存在局部稳定性问题。相比天然工况，蓄水后，最小总应力的拉应力区明显扩展，沿坡体内部逐渐延伸至斜坡前缘。最大剪应变方面，应变增量沿泥岩层发育，说明对这类顺倾边坡来说，在库水作用下，应注意相对软弱层的倾向特征，一旦蓄水，该层极有可能发育为相对不稳定层。泄水工况下，边坡中上部坡表拉应力区贯通，但斜坡中下部拉应力区未贯通，泥岩层内部出现剪应变集中，但量值相比蓄水工况更小，说明对顺倾边坡来说，其稳定性受蓄水影响更大。

5 结 论

本文阐述了不同斜坡结构类型下的边坡在常水位、蓄水位、泄水位3种工况下的变形成因机理，分析了进行流固耦合计算的方法，并选取3个典型边坡进行计算，结论如下：

1) 对反倾岩质边坡而言，拉应力区主要出现在坡表，应力集中以陡缓交界处最为明显，蓄水后，拉应力的分布范围与应力量值明显扩大。最大剪应变方面，与常水位相比，有增加的趋势，最大达到0.064。可以认为，对这种类型的边坡，在水库蓄水后，极有可能导致边坡坡表出现变形。

2) 对上硬下软型边坡而言，在库水作用下，应注意极软层前缘临空情况，一旦蓄水，该层极有可能发育为相对不稳定层。在泄水工况下，斜坡中上部坡表拉应力区贯通，但斜坡中下部拉应力区未贯通，软弱层内部出现剪应变集中，但量值相比蓄水工况更小，说明对上硬下软型边坡来说，稳定性受蓄水影响更大。

3) 对顺倾岩质边坡来说：在库水作用下，应注意相对软弱层的倾向特征，一旦蓄水，该层极有可能发育为相对不稳定层。泄水工况下，边坡中上部坡表拉应力区贯通，但斜坡中下部拉应力区未贯通，泥岩层内部出现剪应变集中，但量值相比蓄水工况更小，说明对顺倾边坡来说，其稳定性受蓄水影响更大。