基于人工势场的无人机集群协同对抗问题研究
杨 皓,张佳乐,裴志明
(长安大学工程机械学院,陕西 西安 710054)
0 引言
随着无人机技术与人工智能技术的发展,新一代人工智能技术与自主技术快速走向战场[1-3],使得无人机协同作战成为可能,多无人机间的协同攻防对抗逐渐成为未来空战的重要模态[4]。
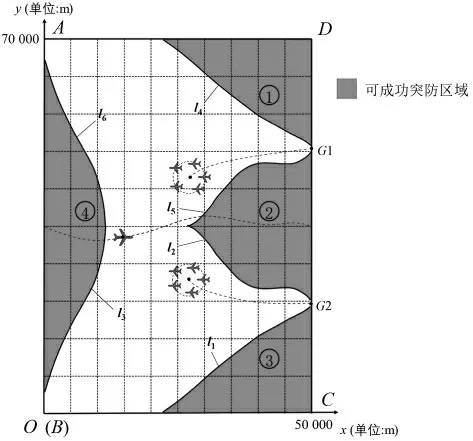
课题小组讨论的对抗区域如图1所示,在图1所示的矩形区域ABCD内,攻击纵深即BC之间的距离为L=50 km,通道带宽即AB之间的距离为M。蓝方作为进攻方,旨在突破红方无人机的拦截成功抵达目的地。红方作为拦截方,在给定的区域内阻止蓝方的突防。可知当蓝方突防无人机与红方至少两架无人机的距离均小于R=300 m时,就认为红方成功拦截了蓝方突防无人机。且红方任何相邻两架无人机的间距相同,红方任何两架无人机的间距需大于30 m,每一架无人机与本集群中至少两架无人机的距离不超过200 m,红方运载机的速度为V红=300 m/s,转弯半径不小于1 000 m,红方无人机的速度为VP=200 m/s,最小转弯半径为RP=350 m。此外,红方运载机与所属无人机集群中至少一架无人机的距离不超过10 km,与任何一架无人机的距离需大于100 m,同时为安全需要,与蓝方的突防无人机的距离需大于5 km。蓝方无人机需在360 s内越过边界CD,否则视为突防失败。蓝方无人机的速度为VE=250 m/s,最小转弯半径为RE=500 m。在整个追击对抗过程中,红蓝双方无人机的速度保持不变,运动的方向可根据机动策略的需要随时改变,但受转弯半径的限制。
如图1所示,假设红方两个无人机集群的起始圆周中心分别位于半径为100 m的G1和G2处,其中DG1=20 km,G1G2=30 km,CG2=20 km。试建模分析蓝方无人机处在ABCD内哪些位置,可使得红方无人机无论采取什么追击策略,都无法阻止蓝方的突防,并找到蓝方无人机相应的最优突防策略。

图1 红蓝双方无人机协同对抗示意图
1 问题分析
问题要求在规定的时间内以及满足相应拦截规则的条件下,建模分析出蓝方无人机处于矩形ABCD内哪些位置时,无论红方无人机集群怎样协同拦截,蓝方无人机总能找到相应策略实现成功突防。由于问题要求是在平面区域内同一高度进行协同对抗,且双方无人机的速度保持不变,速度方向可根据机动策略进行随时改变。因此,考虑将该问题转换为物体在速度势场中吸引与排斥问题。问题解决思路流程如图2所示,步骤概括如下。

图2 问题解决思路流程图
1)根据红蓝双方无人机在对抗中的速度、转弯半径以及规则要求,将至少两架红方无人机与蓝方无人机之间的距离,简化为红方无人机集群中心点距蓝方无人机之间的距离。
2)确定红蓝双方无人机所处的排斥势场与吸引势场,建立人工速度势场模型,基于在MATLAB环境中通过枚举法确定出蓝方无人机可以成功突防的伊始点坐标。
3)调用MATLAB中CFtool工具箱,对上述伊始点的坐标进行基于最小二乘法的多项式曲线拟合,确定出蓝方无人机能成功突防的具体区域,根据仿真结果对比获得蓝方无人机的最优突防策略。
2 人工速度势场模型建立与求解
2.1 拦截模型简化
根据已知条件,当蓝方突防无人机与红方至少两架无人机的距离均小于300 m时,认为红方成功拦截了蓝方突防无人机。同时,假设红方无人机集群时刻处于“最优拦截队形”,即集群中总有两架无人机时刻保持与蓝方无人机距离相同。由条件可知,红方无人机集群圆周半径为100 m,则拦截时刻红蓝双方无人机位置关系如图3所示。根据几何关系,计算得此时蓝方无人机与红方无人机集群圆周中心(后文简称集群中心)的间距,近似为lmax=375 m。此后,在讨论能否成功拦截的问题时,只需判断蓝方无人机至集群中心的距离是否小于lmax即可。因此,后续可利用集群中心点Fi(i=1,2,…,n)来表示运载机所发射的集群。
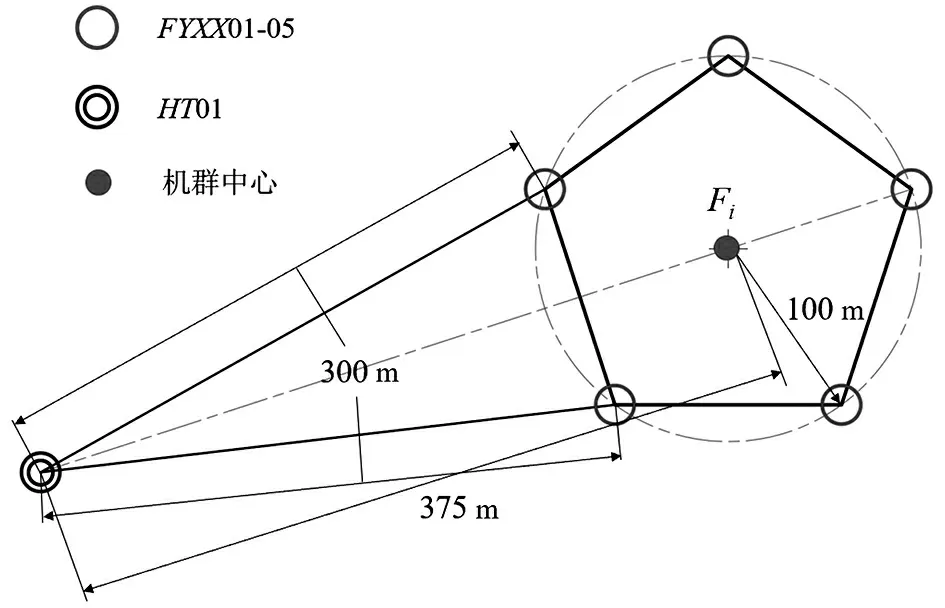
图3 红方无人机集群简化模型示意图
2.2 人工速度势场模型的建立
人工势场法是由Khatib提出的一种比较常用的局部路径规划算法,本质上为一种反馈控制策略,对控制和传感误差有一定的鲁棒性,常用于无人机的路径规划中[5-9]。课题小组基于人工势场的思想,提出一种基于人工速度势场的突防模型与拦截模型,即无人机某一方向上速度的大小直接受其与吸引、排斥势场源距离的影响。
对蓝方无人机来说,由于其突防路径不可超过矩形区域ABCD的上下边界,因此,由矩形的上下边界AD、BC与红方无人机集群共同为其提供速度排斥势场,由矩形右边界CD为其提供速度吸引势场,速度排斥势场不断逼使蓝方无人机远离边界AD与BC,速度吸引势场则使得蓝方无人机朝着CD边线方向不断靠近。对红方无人机来说,由于轨迹不受边界ABCD限制,故仅由蓝方无人机为其提供速度吸引势场,使其不断向蓝方无人机靠近进行拦截。同时,可通过调整速度吸引、排斥势场中的参数,实现双方无人机突防策略或追击策略的改变。由于双方无人机处于移动状态,造成速度势场源随时改变,使得不同位置处的速度势场同样在随时改变,进而导致作用在双方无人机上的场强大小具有随动性,因此,可称该突防—追击策略为随动策略。具体建模过程如下。
如图4所示,以点B为原点,BC方向为x轴正方向、BA方向为y轴正方向建立平面坐标系xOy,由已知条件知 图 中 各 点 坐 标 为A(0,70 000)、B(0,0)、C(50 000,0)、D(50 000,70 000)、G1(50 000,50 000)、G2(50 000,20 000)。设蓝方无人机HT01坐标为H(x1,y1),其广义速度坐标为;红方运载机FY01发射的无人机集群中心坐标为F1(x2,y2),其广义速度坐标为;运载机FY02发射的无人机集群中心坐标为F2(x3,y3),其广义速度坐标为。
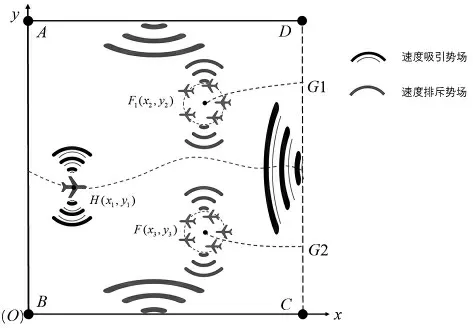
图4 人工速度势场示意图
利用人工势场思想,结合已知数据,建立双方无人机的速度表达式,即突防、拦截随动策略表达式。
①建立H在x、y方向上的速度表达式。
令其在y方向上的速度表达式为:
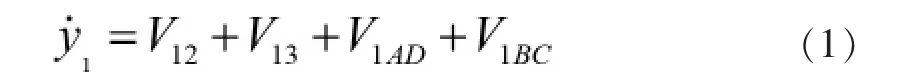
其中,V12、V13、V1AD、V1BC分别为由F1、F2、边界AD以及边界BC对其产生的速度排斥势场,通过分段规划方法及线性映射思路推导获得,其相应公式为:
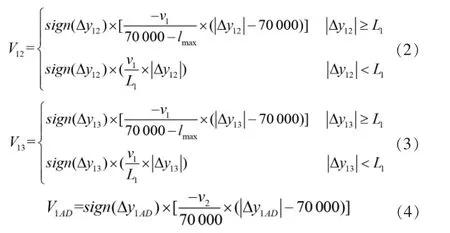
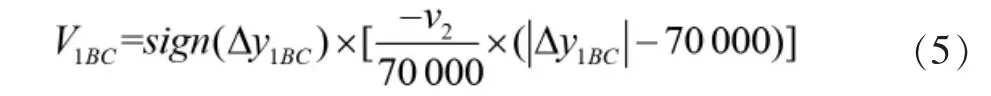
由于H速度大小要求保持不变(VE=250 m/s),即有因此,其由边界CD提供的x方向上速度吸引势场可由如下公式表示:

②建立Fi在x、y方向上的速度表达式。
以F1为例,为实现追击拦截,其运动方向需朝向H,如图5中所示,此时有:

图5 F1速度分解示意图

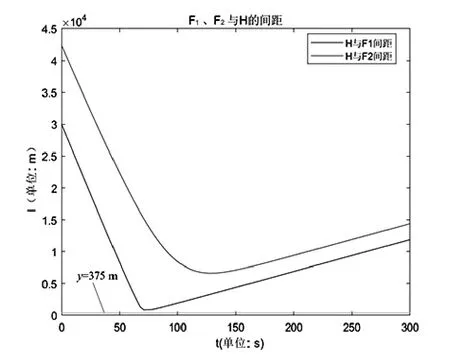
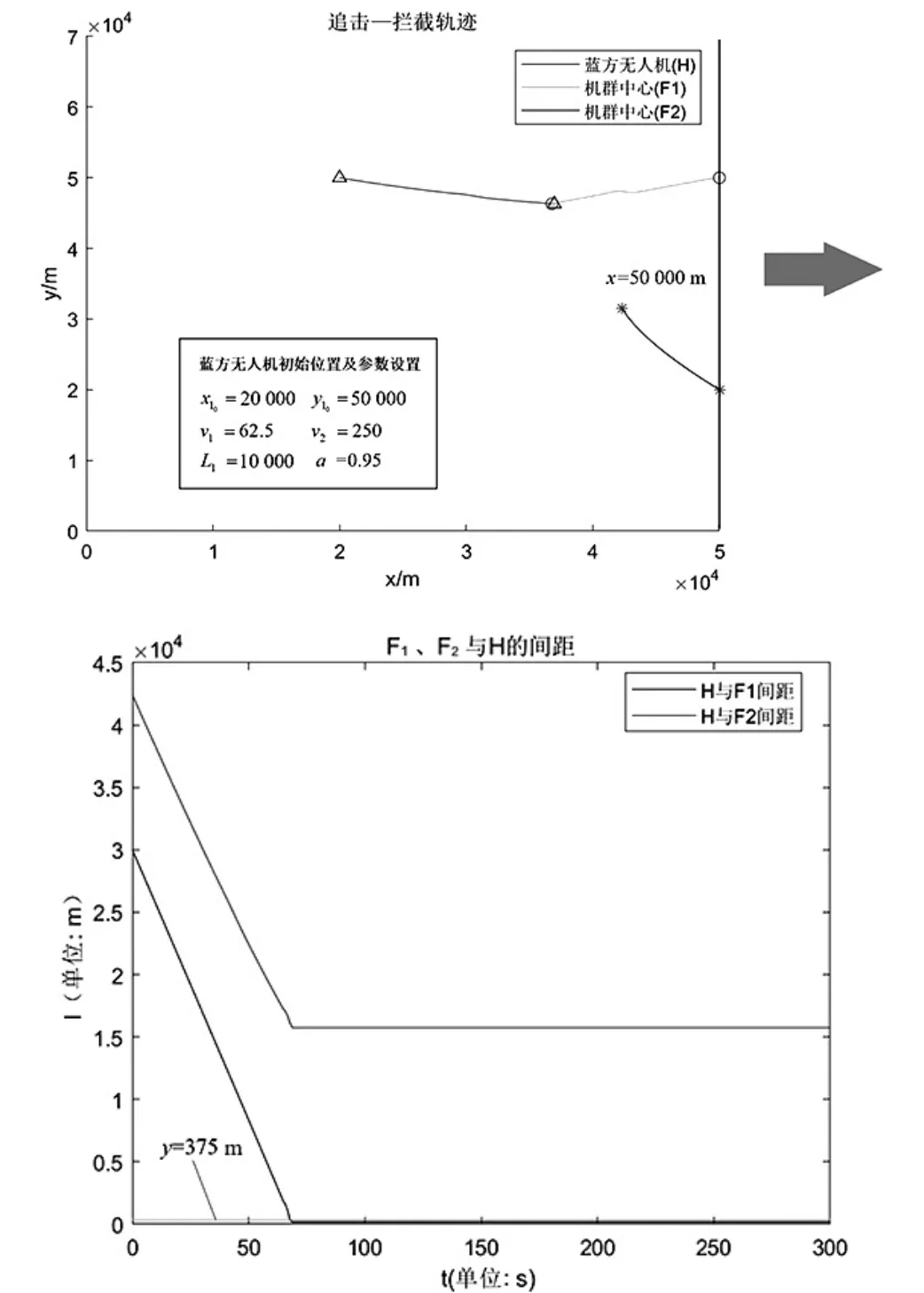
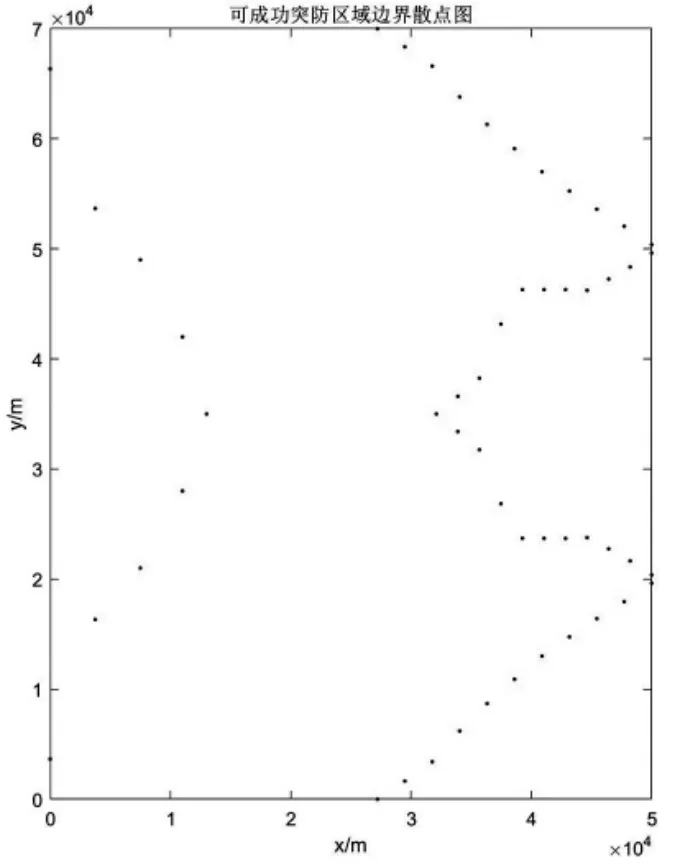
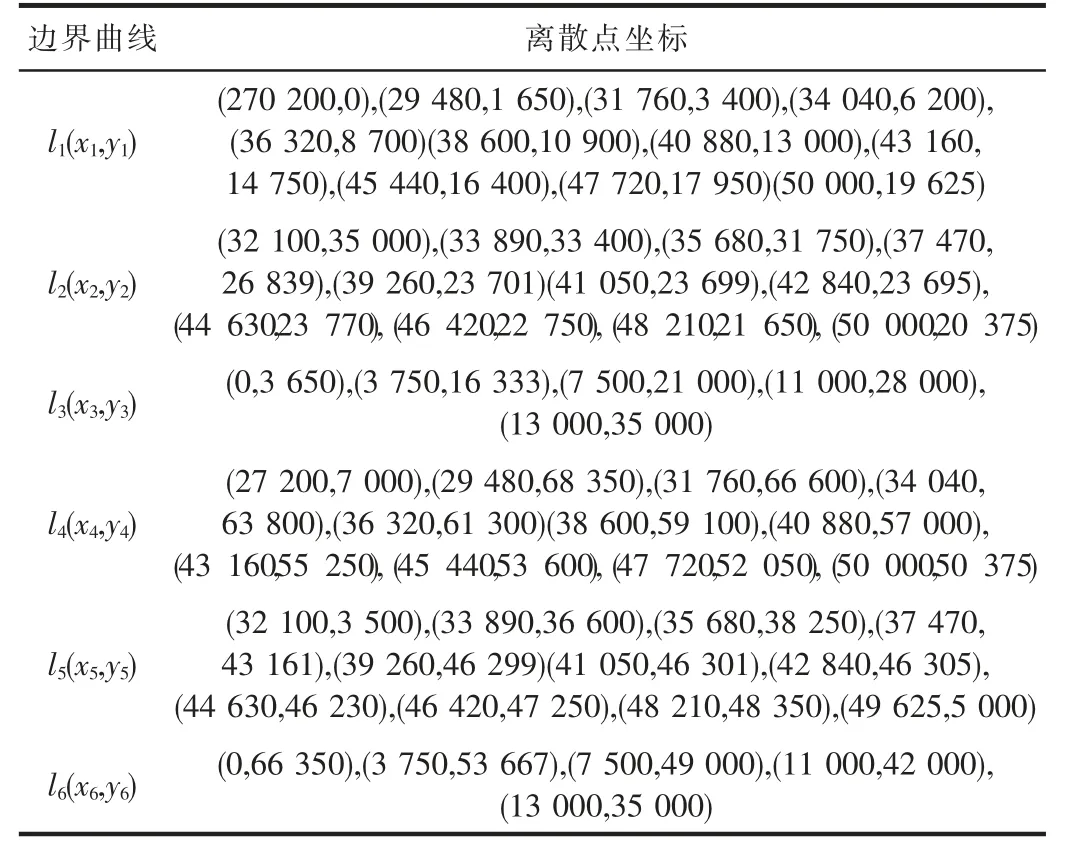
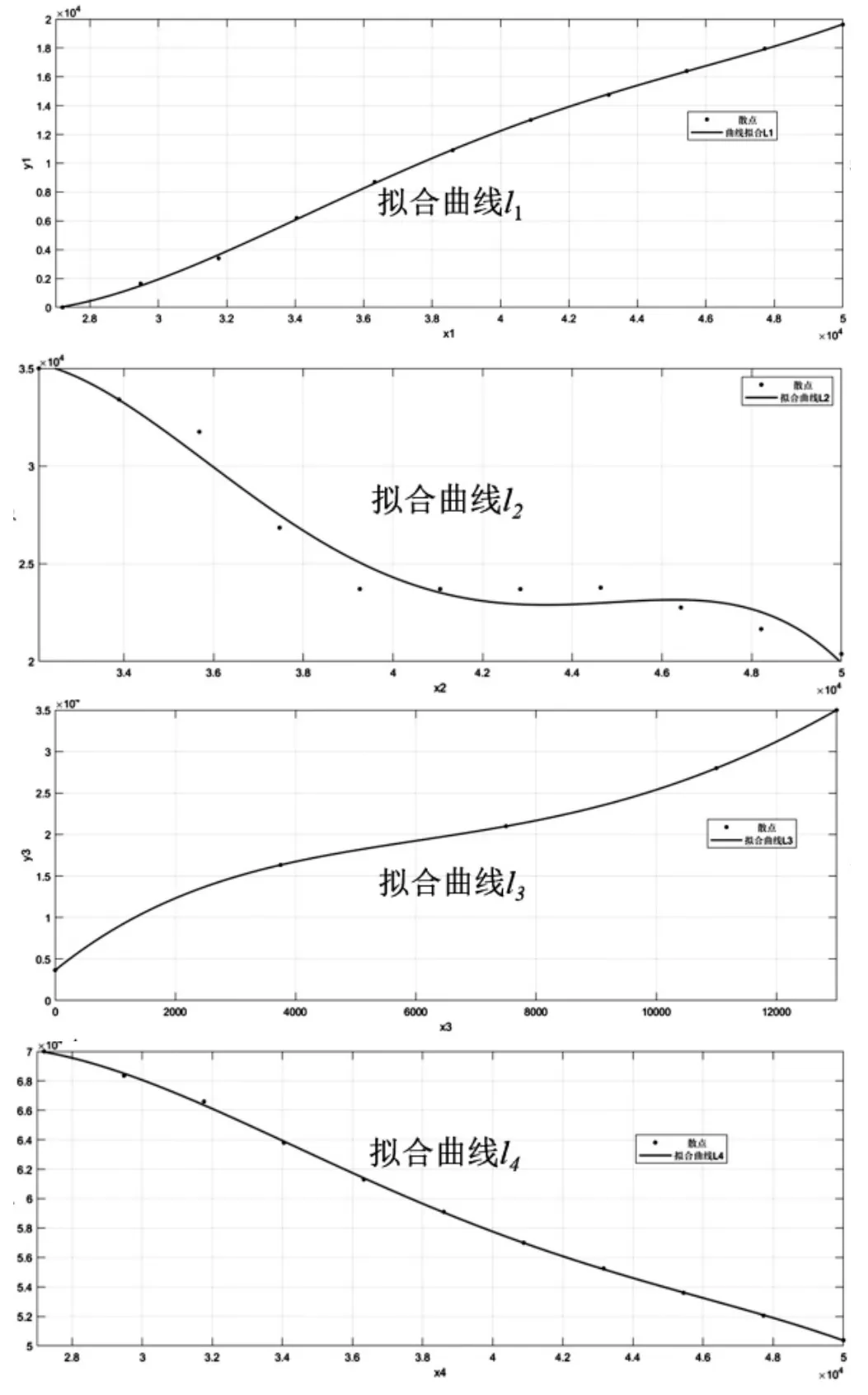
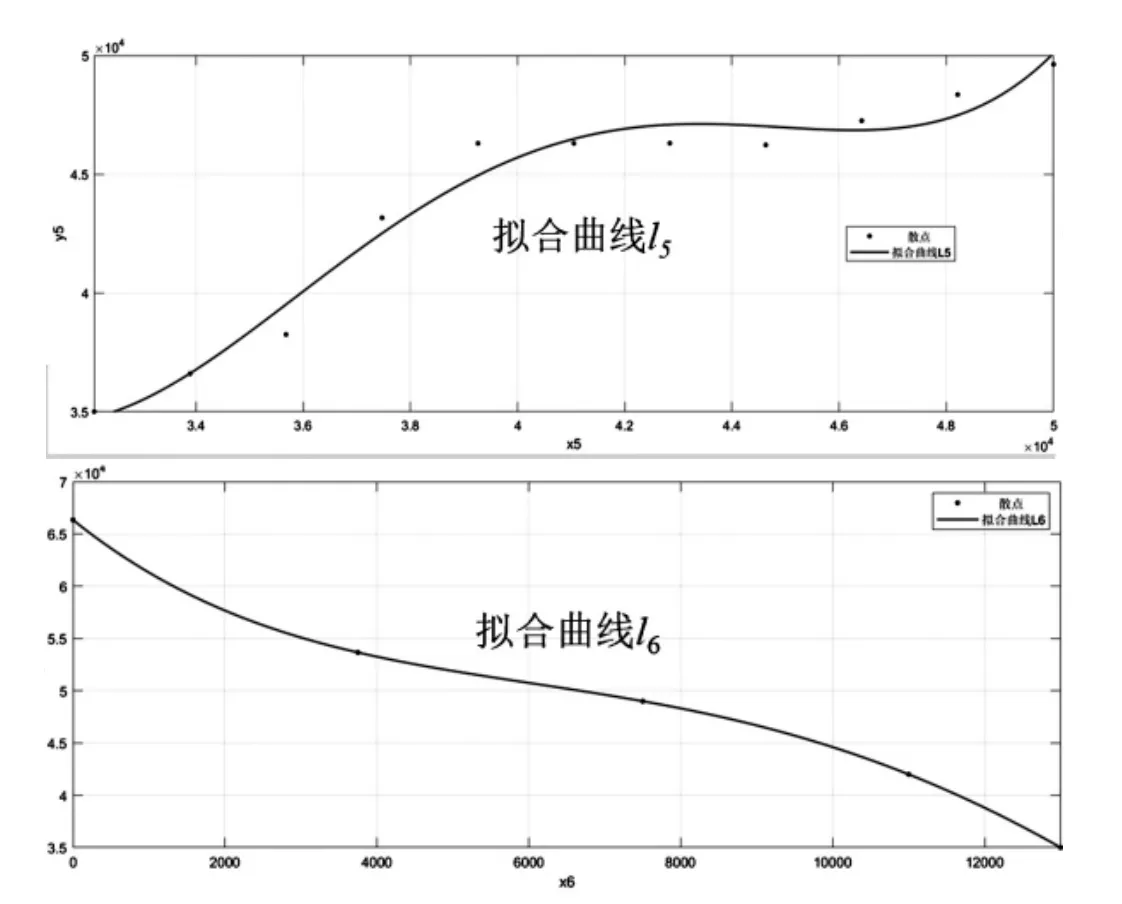
但结合实际考虑,由于Vp 同理,F2的速度表达式为: 由于该速度势场模型中具有多个可调参数,同时运用求解动力学微分方程的思想,可保证红蓝双方无人机各自的运动轨迹依据对方位置实时进行调整,具有良好的随动性。 由2.2中模型可写出该突防—追击模型的运动学方程为: 其初值为: 利用MATLAB中ode45函数对由式(11)、式(12)构成的运动学方程进行求解,并输出360 s内的仿真结果,同时实时输出F1、F2与H的间距值: 由2.1中的简化模型可知,在t<360 s时,若出现l12或l13的值小于lmax(375 m),则证明本次拦截成功。当蓝方无人机初始位置为时,选取不同势场参数时程序输出结果如图6、图7所示。 图6 某一势场参数下蓝方无人机成功突防示意图 图7 改变势场参数后蓝方无人机遭遇拦截示意图 由图6、图7可知,在蓝方无人机初始位置相同的情况下,势场参数的选取影响着蓝方无人机能否突防成功, 势场参数的不同代表着突防策略与拦截策略的不同。 如图8所示,从左至右分别为H、F1、F2速率随时间变化的曲线。由图可知,在仿真过程中,系统时刻满足给定的速度条件(VE=250 m/s、Vp=200 m/s),保证了模型的正确性。 图8 红蓝双方无人机速度检验 为获得H总能成功突防的起始位置所构成的区域,利用枚举法,通过改变H的起始位置以及可调参数v1、v2、b、L1及L2,进行大量自动仿真,获得H刚好运动至边界 CD处时成功突防的H起始位置散点图,如图9所示。 图9 可成功突防区域边界散点图 各离散点坐标如表1所示。 表1 各边界离散点坐标 根据表1中数据,利用CFtool工具箱进行基于最小二乘法的四次多项式函数曲线拟合[10],分别得到如图10所示的6条蓝方无人机总能成功突防的起始位置所构成区域的边界。 图10 六段散点曲线拟合结果 将6条拟合曲线绘制在同一坐标系下,得到蓝方无人机总能成功突防的初始位置区域,如图11所示。 图11 可成功突防初始位置区域示意图 其中,l1-l6六条曲线的表达式分别为: 其所包围的区域①、②、③、④,即为无论红方无人机采用什么样的追击策略,蓝方无人机总能成功突防的初始位置区域。 同时,对不同势场参数下的突防仿真结果对比可得,当蓝方无人机所处y方向上的速度势场相关参数取值为v1≈82.5,v2≈100,L1≈4 000时,为蓝方无人机相应的最优突防策略。 本课题组首先对突防过程中双方无人机的相对位置进行了几何分析,将对抗模型作简化处理;而后基于人工势场的思想,以红蓝双方无人机为研究对象,建立了人工速度势场模型,为使双方无人机具有不同的突防、拦截策略,在该模型中引入了四个可变的势场参数,提高了该模型的准确性与实用性;最后,基于MATLAB编程环境,利用枚举法与最小二乘曲线拟合法确定出该速度势场模型下蓝方无人机总能成功突防的起始位区域;同时,对比分析不同势场参数下的仿真结果可得,当蓝方无人机所处y方向上的速度势场相关参数取值为v1≈82.5,v2≈100,L1≈4 000时,为其最优突防策略。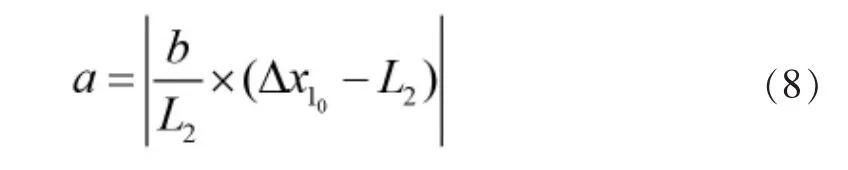
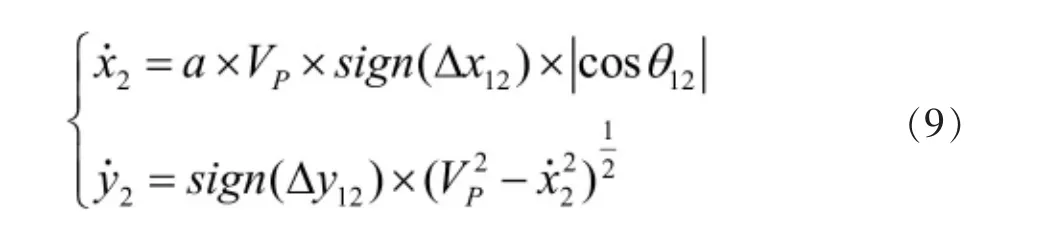
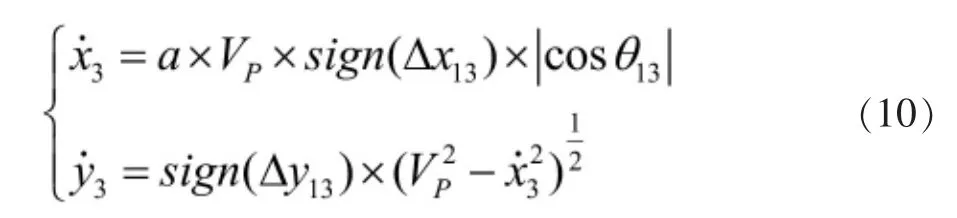
2.3 模型的求解与仿真
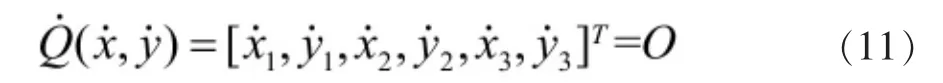

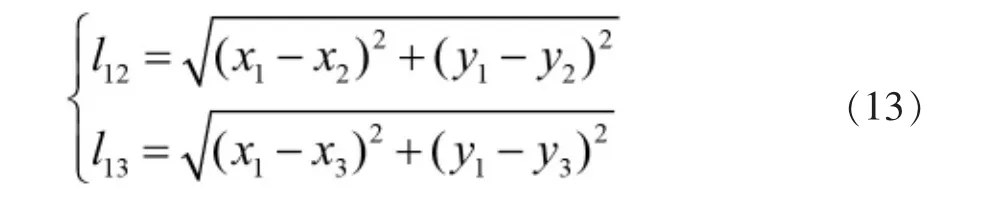

3 基于最小二乘法的多项式函数曲线拟合
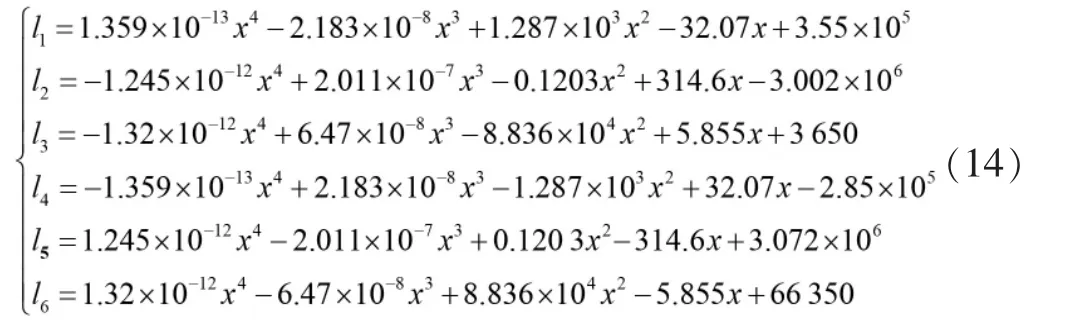
4 结论

