热冲压高强钢不同充氢时间下的氢浓度计算及其与氢脆层关系研究*

张晓欣，陈 扬，黄苏婷，韩先洪，2*

(1. 上海交通大学 材料科学与工程学院塑性成形技术与装备研究院，上海 200030；2. 上海交通大学 材料科学与工程学院模具CAD国家工程研究中心，上海 200030)

0 引言

随着汽车行业对于安全标准和轻量化要求的提升，热冲压高强钢在车身中的应用率显著增加。热冲压是将冷轧后的钢板在900～950℃的温度下保温3～5 min，待板料组织全部转化为奥氏体后，在水冷模具中淬火同时压制成型，获得高强度马氏体零件的一种工艺方法。热冲压工艺可以获得回弹小、强度高的零部件[1]。但材料的强度越高，其氢脆敏感性越高，产生氢致延迟断裂的风险也越大[2-3]，具体表现为氢在加热、酸洗、服役等过程中渗入板料，与残余应力作用一定时间后，引起机械性能下降，产生裂纹，并最终导致零件损伤、断裂[4]。

高强钢的氢脆问题已引起国内外学者的广泛关注。Wang等[5]对比了QP980和QP1180淬火再分配高强钢的抗氢致延迟断裂性能，结果显示： 其抗延迟断裂能力随强度增加而降低。Depover等[6]通过研究TRIP钢、DP钢、FB钢和马氏体钢这4种热冲压高强钢充氢后的力学性能，分析不同组织对高强钢氢脆敏感性的影响，发现了马氏体钢对氢的敏感性最高，奥氏体对氢敏感性最低；Venezuela等[7]研究了MS1700新型先进高强钢在不同充氢环境中的氢脆现象，发现其在3.5%(质量分数)的NaCl中的氢脆敏感性远低于在0.1 mol·L-1NaOH和0.1 mol·L-1HCl溶液中的氢脆敏感性，拉伸断口呈现脆性剪切断裂特征；Li等[8]采用高强度马氏体不锈钢PH13-8Mo研究了充氢时效影响下的断裂形式，指出有氢时断口截面外部表现出脆性的准解理断裂，中心区域为韧性断裂，且脆性断裂区深度和脆性断裂区面积分数随氢作用时间延长而增加。

材料的氢脆现象与氢浓度分布密切相关，但氢具有活性高、体积小、扩散能力强的特点，很难测定或观察氢扩散及运动过程，因此采用数值模拟是研究氢扩散行为的有效方法[9]。Diaz等[10]根据扩散方程和传热方程的相似性，在Abaqus软件中建立与传热类似的氢扩散子程序，将氢运动与弹塑性材料的力学响应耦合起来。Olden等[11]利用有限元内聚单元模拟氢致裂纹的萌生，研究了X70管线钢氢扩散与断裂的关系，指出焊接产生的热影响区易于断裂，具有较强的氢脆敏感性。Mente等[12]则使用Ansys模拟了氢扩散影响下，不同相之间裂纹萌生、扩展的过程。注意到目前针对热冲压高强钢的氢扩散与分布计算的研究较少，现有研究尚未建立氢浓度与氢脆层的关系。本文分别利用理论计算和ABAQUS有限元软件模拟了氢在热冲压高强钢B1500HS中的扩散，分析氢的扩散和浓度分布规律；通过电化学充氢、拉伸试验以及断口微观观测，将试验结果与模拟结果联系起来，获得断口氢脆层分布与氢浓度的对应关系。

1 氢扩散理论计算与数值模拟

1.1 热冲压钢中的氢扩散理论计算

菲克第一定律假定扩散物可稳定地从高浓度扩散到低浓度，且扩散过程中各处的浓度变化与时间无关，即：

(1)

实际上，稳定态扩散的情况很少，大部分扩散属于随时间变化的非稳定态扩散，即满足菲克第二定律：

(2)

当氢扩散源为非点源时，其扩散过程宏观上可以近似为一维扩散，(2)式中的菲克定律可简写为：

(3)

针对一般的电化学充氢过程，近似满足如下边界条件： 当t=0时，扩散介质中氢浓度为0；在氢扩散起始面，氢浓度始终为Cs；在扩散介质中距离扩散起始面较远的位置，氢浓度为0。

通过Laplace变换求解C(x，t)，得到沿扩散深度方向氢浓度随时间变化的误差函数解[13]：

(4)

1.2 热冲压钢中的氢扩散有限元模型

以有限元软件ABAQUS为平台开展氢扩散数值模拟。ABAQUS遵循的质量扩散方程dC/dt=-ΔJ是菲克定律的扩展，物质扩散过程中除了受到浓度梯度的影响，温度和应力梯度也有利于氢的扩散。假定在非均匀介质中，化学势梯度是氢扩散的驱动力，给出了瞬态氢扩散方程[14]：

(5)

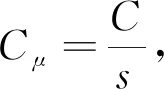
针对氢由试样表面向内部渗透扩散的现象，建立沿厚度方向的平面模型，如图1所示。几何模型尺寸为1.4 mm×6.0 mm，其中1.4 mm代表板料厚度，最小单元尺寸为10 μm，网格共划分为8.4×104个单元。采用二维四节点四边形的DC2D4单元和瞬态分析过程进行氢扩散计算。模型两侧为氢扩散起始位置，氢浓度为Cs，试样内部的初始氢浓度为0。

图1 氢扩散有限元模型

2 氢扩散试验

2.1 试验材料

本试验采用B1500HS热冲压用钢，厚度为1.4 mm，化学成分及含量见表1。热处理前的原始组织为铁素体和珠光体。加热到920℃，保温5分钟得到完全的奥氏体组织，水淬后为全马氏体。

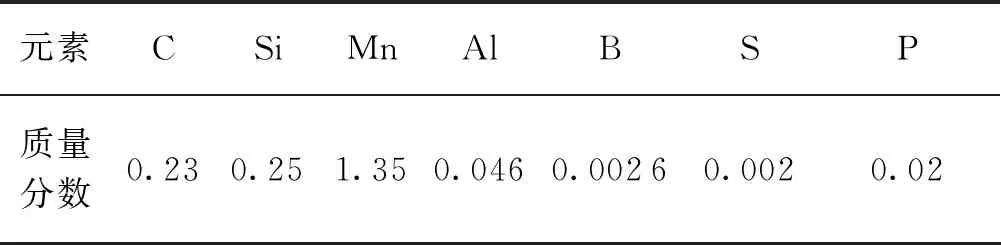
表1 B1500HS钢化学成分 %

2.2 充氢试验

原始热冲压试样中的氢含量很低，需要外界充氢增加试样中氢的浓度，本试验采用电化学充氢法对B1500HS的氢扩散现象进行研究。通过电源、导线、铂丝、试样和电解液构成电化学充氢回路。其中，铂丝作为阳极，试样作为阴极，电解液为500 mL物质的量浓度为0.5 mol·L-1的稀硫酸，添加硫脲作为抑制氢原子结合成为氢气分子逸散的毒化剂，提高氢原子渗入试样的效率，试验使用0.001 A充氢电流(充氢电流密度为0.422 mA·cm-2)。

2.3 拉伸试验及断口观测

试样在充氢300， 780， 1 800 s后，继续保持电解充氢状态，防止氢溢出试样，使用INSTRON拉伸试验机以9.6 mm·min-1的拉伸速率快速拉断，从而获得不同充氢时间下热冲压钢的宏观力学性能及微观断口形貌变化。使用充氢后的延伸率损失表示脆性指数(Embrittlement Index, EI)[6]，以评估试样氢脆敏感性程度，该指数表达式如下：

(6)

式中：δAir和δHydrogen分别表示充氢前后试样的延伸率。

参照GB/T 228—2010设计出试验所需标准拉伸试样，如图2所示。通过给试样开缺口来控制断裂位置，获得平整断口，缺口应力集中系数为3.1。在电解充氢过程中，试样表面除用来测量应变的标距段外，均采用绝缘胶带包裹(图2中深色区域)。使用扫描电子显微镜(Scanning Electron Microscope, SEM)观测不同充氢时间下试样的拉伸断口，分析其微观形貌差异，研究氢浓度分布对热冲压钢断口形貌的影响。本试验采用VEGA LaB6扫描电子显微镜进行观测试验。

图2 B1500HS缺口拉伸试样(单位： mm)

3 结果分析与讨论

3.1 热冲压钢中氢扩散的理论计算结果和有限元模拟结果

本节建立了氢在热冲压高强钢中扩散的有限元模型，研究氢在高强钢中分布的规律。氢在马氏体热冲压高强钢中的扩散系数D=3.3×10-10m-2·s-1[15]，使用试样充氢饱和后的热脱附光谱(Thermal Desorption Spectroscopy, TDS)测得的平均氢浓度作为试样表面的初始氢质量分数Cs=1×10-5。氢扩散的时间分别为t1=300 s，t2=780 s，t3=1 800 s。同样的氢扩散参数也适用于式(4)所示菲克第二定律的误差函数解。图3为根据式(4)得到的氢扩散误差函数解(曲线图)和有限元解(散点图)的结果，表示不同氢扩散时间下，沿深度方向的氢浓度分布。氢在浓度梯度的驱动下，由材料表面向材料内部进行扩散。由图3可知，两种解法得到的结果非常接近。氢扩散的误差函数解法已经被广泛应用[14，16]，由本试验对比可知： 使用Abaqus有限元模拟热冲压高强钢中的氢扩散具有较好的可信度。

图3 不同充氢时间沿扩散深度方向变化的氢浓度分布

图4为有限元模拟得到的氢浓度梯度分布云图，由图3和图4可知： 氢从试样外表面向内扩散，氢浓度分布呈现递减规律。随着氢扩散时间的增加，氢在试样中的扩散距离和高浓度氢聚集的区域面积进一步扩大，但氢浓度梯度有所降低。如果氢扩散时间足够长，整个试样中的氢浓度将与环境氢浓度一致。

(a) 300 s

3.2 不同充氢时间下试样的宏观力学性能

本节通过单向拉伸试验分析不同充氢时间下材料的氢脆现象。试样在电化学充氢不同时间后快速拉伸，得到热冲压高强钢应力应变曲线，如图5所示，表2则是不同充氢时间对应的抗拉强度、延伸率以及脆性指数EI。由图5，表2可知： 随着充氢时间的增加，材料的抗拉强度和延伸率也在逐渐降低。仅充氢300 s，其强度为1 406 MPa，较未充氢试样降低13.8%，延伸率为2.37%，氢脆指数达到58.6%；在充氢780 s后，抗拉强度降为1 196 MPa，延伸率降为1.08%；充氢1 800 s后，抗拉强度减小到1 118 MPa，与未充氢试样相比损失31.5%，延伸率仅为0.94%，氢脆指数升至83.6%。随着氢原子由试样表面向试样内部扩散时间的延长，进入试样的氢原子数目逐渐增加，试样中氢浓度上升，最终引起了材料强度、塑性的降低，发生氢脆现象。

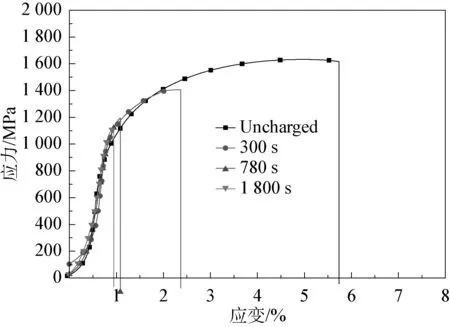
图5 不同充氢时间后拉伸的应力-应变曲线

表2 不同充氢时间后拉伸的抗拉强度和延伸率

3.3 断口形貌及氢脆层分析

图6(a)～6(c)分别为热冲压高强钢在充氢300， 780和1 800 s后，快速拉伸得到的断口形貌图。该形貌图取自沿试样厚度方向靠近表面的位置，其中实线表示断口边缘，即试样表面，也是电化学充氢试验中与电解液接触的平面，即渗氢起始面。图6中可以观察到充氢不同时间后，试样断口边缘位置向内产生了光滑氢脆层，且随着充氢时间的延长，氢脆层的深度也在扩大，但是断口内部依旧是韧性断裂，有小且深的韧窝。每组试样选取50处位置量取氢脆层厚度，得到： 充氢300 s后，氢脆层厚度为14～20 μm；充氢780 s，其氢脆层厚度基本在27～42 μm之间，与充氢300 s后的氢脆层相比略有增加；充氢1 800 s后的氢脆层厚度已经可以达到31～50 μm。

图6 充氢不同时间后拉伸断口边缘形貌

图7为试样断口氢脆层平均厚度柱状图，充氢300， 780和1 800 s后，断口氢脆层的平均厚度分别为18， 30和43 μm。充氢时间越长，通过电化学还原、渗入试样中的氢就会扩散到更远的位置，因此受氢扩散影响的氢脆层厚度也就越大。尽管根据模拟结果显示： 同一深度不同位置的氢浓度分布是一致的，因此氢脆区深度应该是均匀的，实际上由于材料各处微观缺陷，造成局部氢浓度过高，在图7中使用误差棒表示所有统计结果与平均厚度的差距。需要指出，在试样中并不是只有脆性区才有氢。实际上氢原子遵循化学势梯度扩散，在试样中存在由高浓度向低浓度连续扩散的趋势，只是靠近试样表面位置处的氢浓度更大，达到了能使试样断口形成脆性断裂特征的临界氢浓度，而试样截面靠近中心的位置虽然也有氢分布，但氢浓度较低，因此依旧保持韧性断裂特征，从而整个断面呈现两种不同的断裂形式。

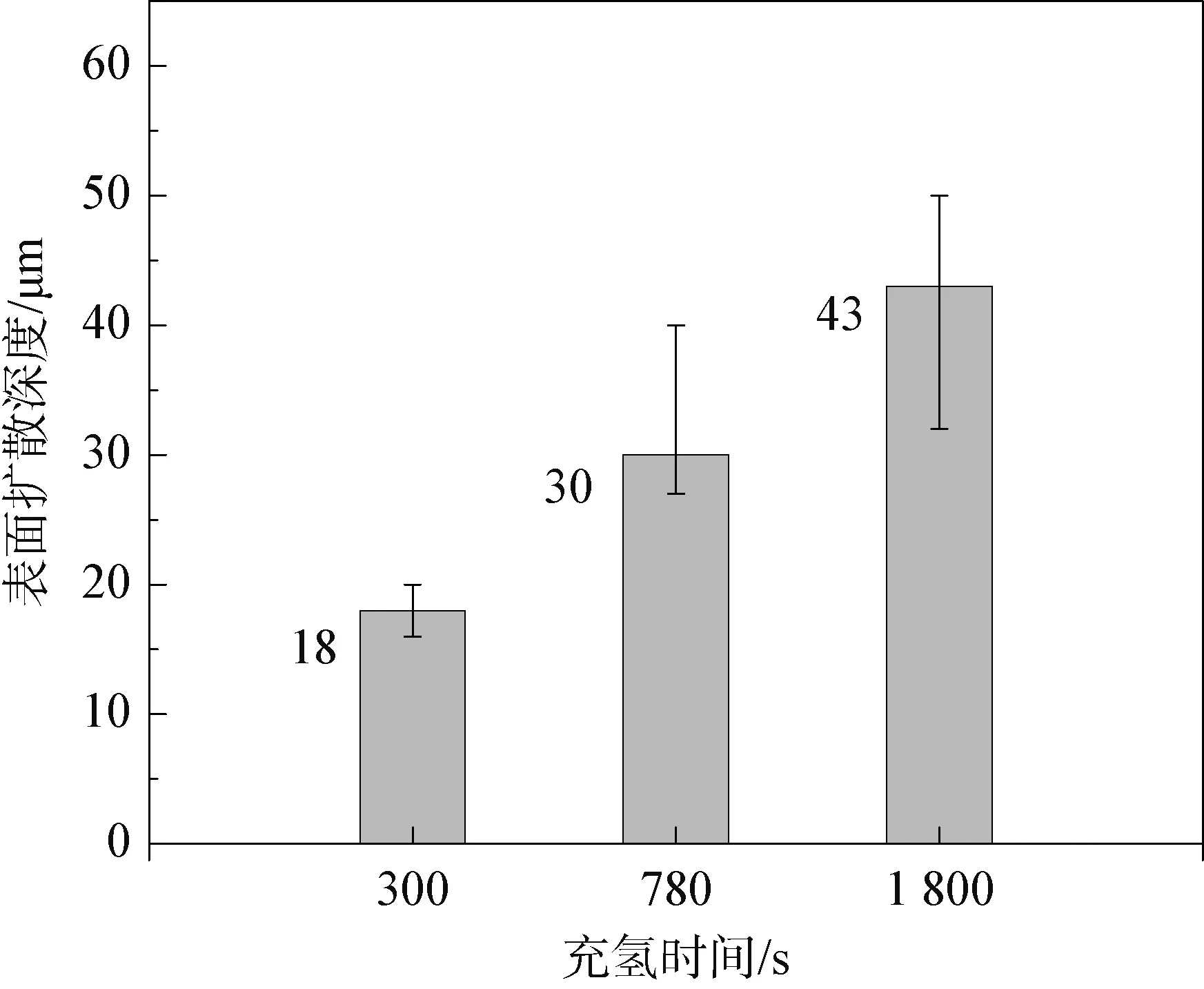
图7 不同充氢时间氢脆层深度

通过数值模拟，可得到断口各个位置在不同时间下的氢浓度值，如图8所示。研究3个典型充氢时间后的氢脆层边界所对应的氢浓度值发现： 充氢300 s，氢脆层深度18 μm处，对应的氢质量分数为8.18×10-6；充氢780 s，氢脆层深度30 μm处，对应的氢质量分数为8.10×10-6；充氢1 800 s，氢脆层深度43 μm处，对应的氢质量分数为8.23×10-6。非常有趣的是： 3种情况下，氢脆层边界对应的氢质量分数接近，均为8.20×10-6左右。张惠臻等[17]研究指出： 慢应变拉伸速率下氢有足够的时间运动到孔洞、夹杂等易形成高应力的位置，促进外力作用下的裂纹扩展，因此试样截面整体呈现脆性断裂特征。而本试验中的拉伸试验是在快应变速率下进行的，且缺口试样断裂更快，拉伸过程中几乎没有产生应力诱导氢扩散，因此只有达到临界氢浓度的位置才会在断裂后呈现脆性特征。通过氢脆层深度和有限元的模拟计算，可以预测，对于本试验所采用的热冲压钢B1500HS，引起脆性开裂的临界氢质量分数约为8.20×10-6。

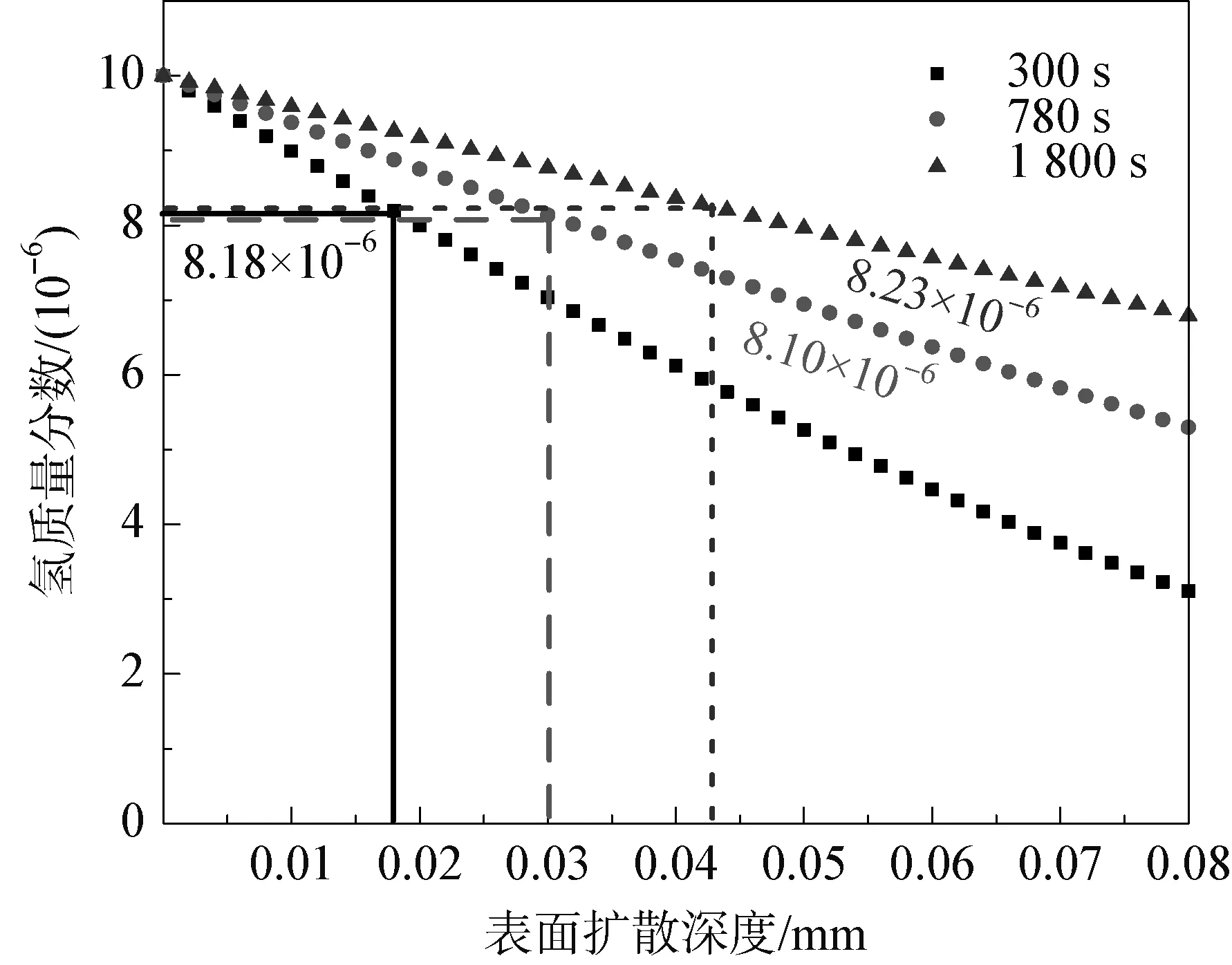
图8 模拟结果中氢脆层厚度对应的临界氢浓度

4 结论

本文以热冲压高强钢B1500HS为试验对象，利用ABAQUS模拟不同充氢时间下氢的扩散和浓度分布，并开展氢脆试验与断口微观形貌观测，得到以下结论。

1) ABAQUS模拟氢扩散曲线显示试样从外向内扩散氢浓度分布呈非线性递减规律，随着氢扩散时间的延长，试样中的氢扩散距离和高浓度氢分布面积均增大；

2) B1500HS的力学性能随着充氢时间的增加而下降，充氢1 800 s的试样强度仅为1 118 MPa，塑性为0.94%，塑性损失达到83.6%，氢脆敏感性高；

3) 随着充氢时间的增加，热冲压钢拉伸断口出现两种不同的断裂模式。断口边部为光滑的氢脆层，呈现脆性断裂特征，断口中心位置则出现韧窝这一韧性断裂特征，且氢脆层的平均厚度从充氢300 s的18 μm，扩大到充氢1 800 s的43 μm；

4) 结合实际断裂氢脆层尺寸和氢扩散有限元模拟，得出引起B1500HS脆性开裂的临界氢质量分数约为8.20×10-6。试样中局部氢质量分数超过8.20×10-6，产生脆性开裂，而低于此临界值时，产生韧性开裂。