尾翼EFP成型及气动的数值模拟
丁 丰,赵太勇,杨宝良,付建平,印立魁,陈智刚,王维占
(1 中北大学机电工程学院,太原 030051;2 中北大学地下目标毁伤技术国防重点学科实验室,太原 030051;3 西安现代控制技术研究所,西安 710065)
0 引言
EFP因其不受炸高限制,能从100~150 m距离处对目标发起攻击,近年来国内外学者进行了大量理论与试验研究。从EFP形成机理出发,Li等[1]研究了环形多点起爆对EFP成形特性的影响。Berner,Rondot 等[2-3]对EFP的飞行稳定性和终点弹道进行了一系列的分析,总结出具有良好飞行稳定性的EFP形状,如双裙体,尖拱形头部等;Liu等[4]研究了EFP的气动特性,提出尾翼结构能够有效改善EFP的飞行稳定性,并减少EFP的飞行阻力;任芮池等[5]应用工程计算方法系统研究准球形、杆式、单尾裙EFP的气动参数随特征尺寸的变化规律,并分析了EFP的升阻力系数随攻角的变化情况;门建兵等[6]采用AUTODUN-3D软件对异形壳体和多点起爆EFP进行研究,得到不同形状尾翼的侵彻体;张孝忠等[7]研究了刻槽药型罩对EFP成形的影响,得到了不同长径比的尾翼EFP;龙源等[8]研究了多点起爆对双层药型罩成形及侵彻的影响,结果表明当起爆点数在4~8时,双层药型罩EFP战斗部能够形成具有较好空气动力学特性的侵彻体;刘健峰等[9]研究了偏心起爆对EFP成形及气动的影响;时党勇,唐平江等[10-11]研究了壳体对EFP形成尾翼的影响;沈慧铭,陆鸣,李成兵等[12-14]研究了多点起爆对EFP成形的影响。
目前公开的文献主要研究壳体材料和形状,药形罩材料和形状,装药等对EFP成形的影响。但对尾翼EFP的成型及气动的综合评判还鲜有报道。文中利用LS-DYNA获得尾翼EFP,通过UG逆向工程得到EFP的几何模型,然后利用FLUENT软件对EFP进行气动分析,得到最利于发挥EFP终点效应的起爆半径。
1 尾翼EFP成型数值模拟
1.1 战斗部结构设计
壳体外表面为正六边形,外接圆直径120 mm,为减少影响因素,省略顶部壳体[15],装药高度Hw=100 mm,采用六点起爆的方式,爆点在六边形的对角线上,装药直径为D=100 mm,药形罩的外半径为151 mm,内半径为160 mm,战斗部结构示意图如图1所示。
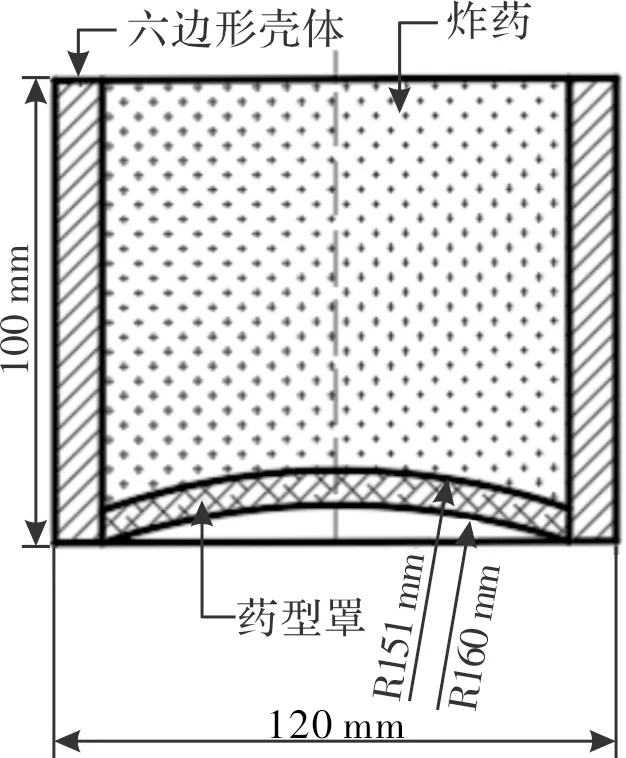
图1 战斗部结构示意图
1.2 尾翼EFP成形数值模拟
为得到清晰的尾翼形状,采用Lagrange算法。利用True Grid软件建立三维有限元模型,网格类型均使用Solid164八节点六面体单元。在炸药、壳体、药型罩相互之间均使用自动面面接触。壳体材料为45#钢,药型罩为紫铜,为了模拟能承受大应变、高应变率的材料,其本构关系模型均采用Johnson-Cook模型。主装药选用8701,选用HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程来描述,其主要材料参数见参考文献[15]。图2为战斗部计算的初始网格。

图2 聚能装药战斗部计算模型
数值模拟总共计算了中心点起爆及不同起爆半径下EFP的成型,图3为各工况下的成型情况。
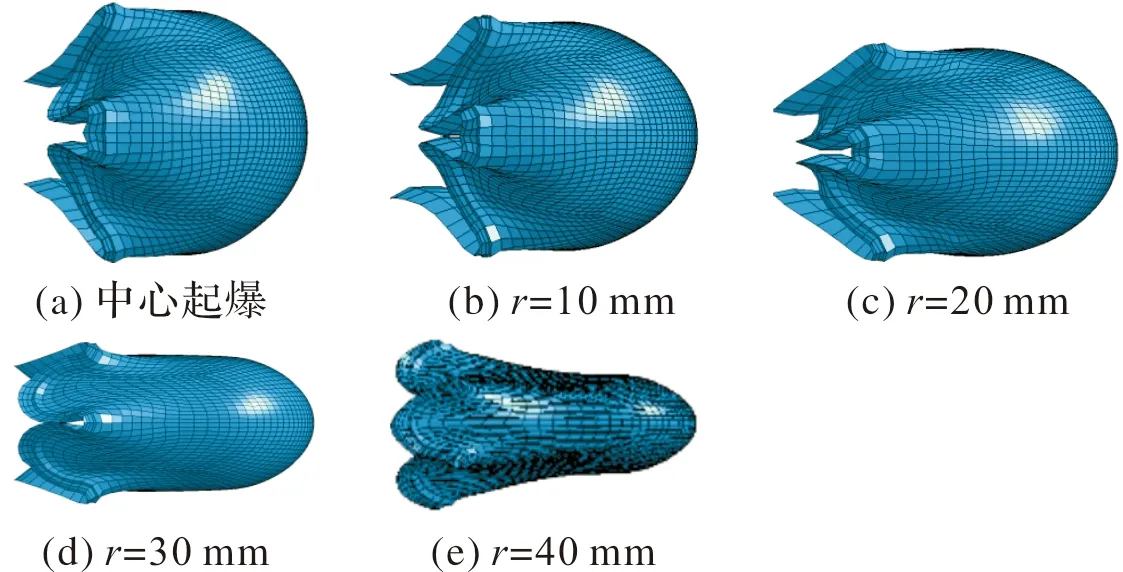
图3 各工况EFP成型
2 尾翼EFP气动特性计算模型
2.1 气动特性数值计算模型
由于LS-DYNA并不能直接对爆炸成型弹丸进行气动分析。因此将计算得到的爆炸成型弹丸在LS-PREPOST中导出STL格式,将模型导入UG中进行逆向建模,得到EFP的几何模型。尾翼EFP的几何外形复杂,曲率变化大,因此采用Mesh划分为四面体网格,由于几种工况下的EFP模型处理方法一致,图4仅给出起爆半径r为40 mm时EFP的几何模型及有限元模型。

图4 EFP模型
将模型导入Fluent进行边界条件设置。研究物体的运动速度小于0.3Ma时的气动特性可忽略空气的可压缩性。文中研究EFP的运动速度在4Ma~6Ma之间,因此需考虑空气的可压缩性。使用双精度计算,选用Density-based求解器,将空气选为理想气体。为适应空气的高马赫数流动,将粘度模型选为Sutherland。湍流模型选用k-omega双方程模型,考虑空气的能量变化,打开能量方程。将流体入口设置为压力远场。
2.2 EFP空气动力
EFP在空气中飞行时,受到空气动力的作用,空气动力的大小取决于EFP的外形、飞行速度及攻角。研究EFP的气动外形有利于提高飞行过程中的稳定性及精度。
弹丸在空气中飞行时,弹轴与速度的夹角称为攻角,攻角所在的平面称为阻力面,如图5所示,以弹丸质心为坐标原点建立右手笛卡尔坐标系oxyz,ox轴与弹丸速度方向相反,oy轴在阻力面内且与ox垂直,oz轴则与阻力平面垂直。作用在弹丸P点上的空气动力R在ox轴方向上的投影为Rx,称之为正面阻力;在oy轴方向上的投影为Ry,称之为升力;在oz轴上的投影为Rz,称之为侧向力。弹丸都会有正面阻力,如有攻角还会产生升力。
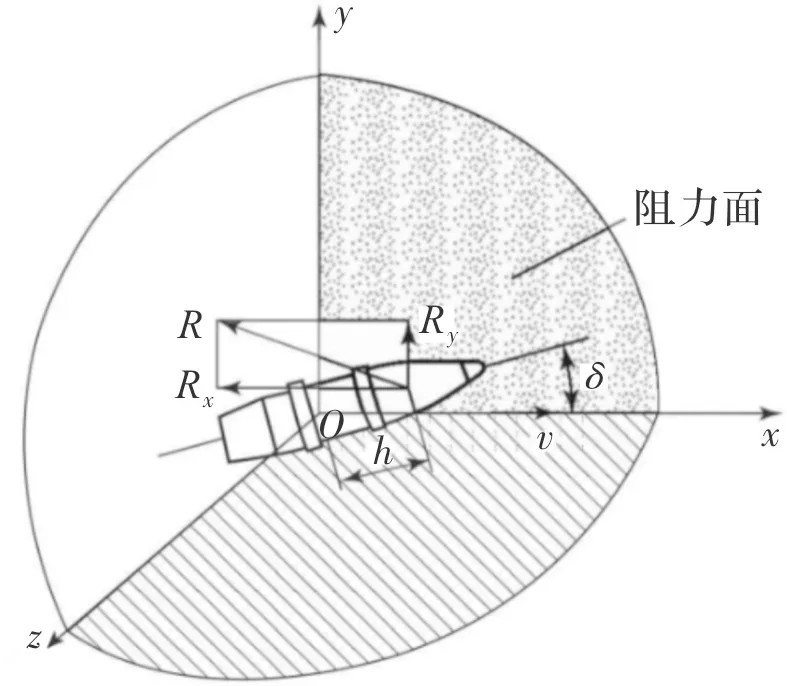
图5 作用在弹丸上的空气动力
根据空气动力学规定,上述空气动力可以表示为:
(1)
式中:p为空气密度;S为弹丸最大横截面面积;v为弹丸飞行速度;Cx为正面阻力系数;Cy为升力系数;Cz为侧向力系数。
若压心P在弹丸头部与质心之间,此时升力与正面阻力的合力引起弹丸质心偏转的力矩Mz称之为翻转力矩,若压心在弹底与质心之间则力矩Mz称之为稳定力矩。EFP的稳定性通常用稳定储备量B来表示。即:
(2)
式中:xp,Cp分别为弹丸阻力中心至弹顶的绝对、相对距离;xs,Cs分别为弹丸质心至弹顶的绝对、相对距离;l为弹丸全长。
对于尾翼稳定的弹丸,应尽量使空气动力对弹丸质心的力矩为稳定力矩,及B>0,良好的尾翼稳定弹丸,其稳定储备量至少在15%~28%。稳定储备量是决定弹丸能否以预设攻角到达瞄准点的一个重要参量。
3 计算结果及分析
3.1 不同起爆半径对EFP成形的影响
多点起爆时,在爆轰发生的一瞬间,每一个起爆点所引起的爆轰以球面波的形式传播,随着爆轰波的传播,相邻位置的爆轰波会在其对称面位置上相遇,并发生激烈碰撞,形成马赫波。在爆轰碰撞区域内压力增加,炸药爆轰更加完全,相当于增加了炸药爆轰的局部能量释放。在药型罩与马赫波接触的微元上,压力会比附近微元高,离马赫区越远,其药型罩上的压力也会随之降低,正是由于药型罩表面微元上的这种压力梯度的变化,导致折叠尾翼的形成。多边形壳体对尾翼的形成也有一定的增益作用。表1是多点起爆下EFP成型增益情况,EFP的平均速度增益、长径比增益都是对单点起爆而言。
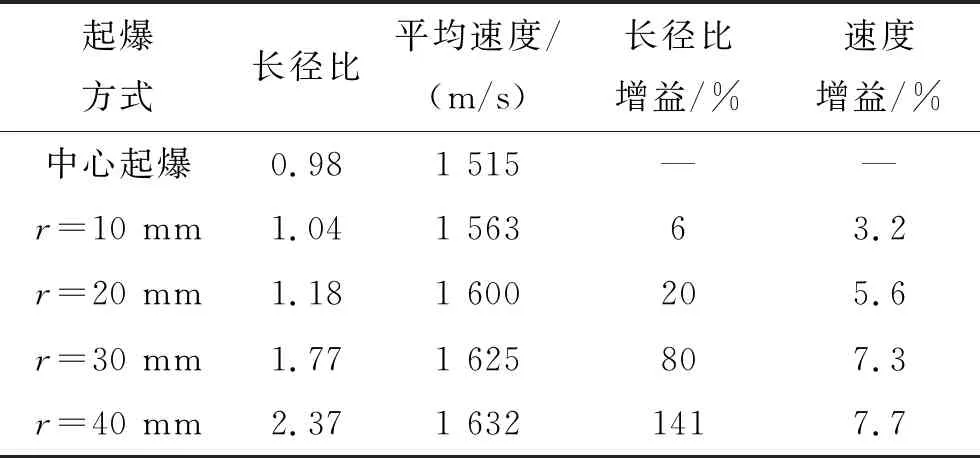
表1 各起爆方式下EFP的参数
3.2 起爆半径和攻角对阻力系数的影响
图6展示了4种EFP的阻力系数随攻角的变化曲线。
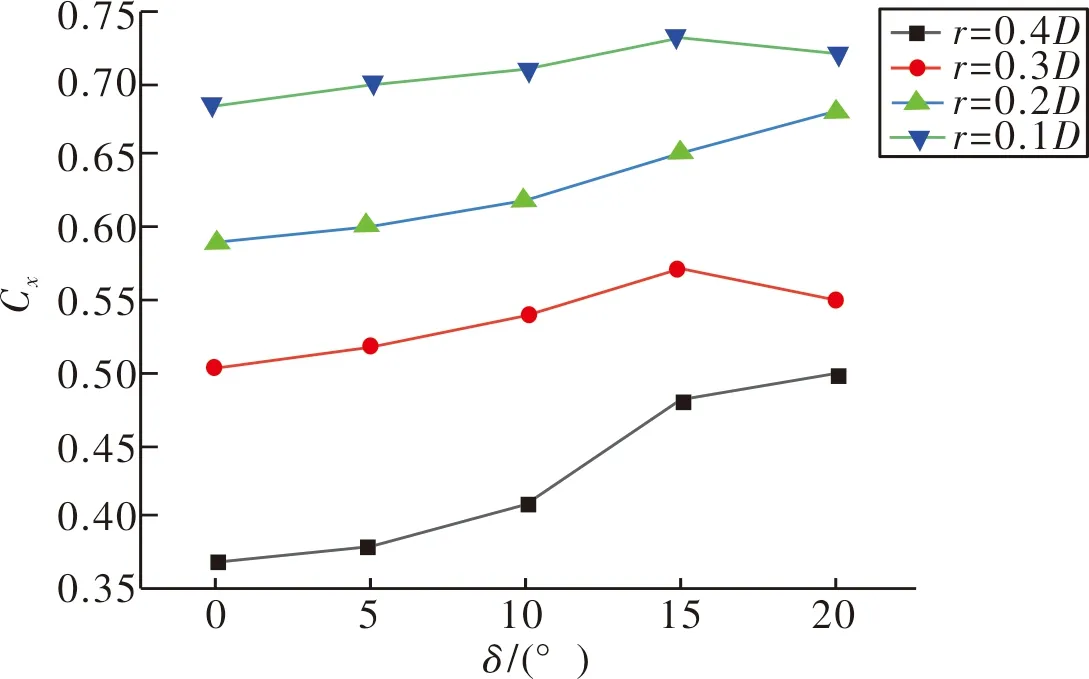
图6 阻力系数变化曲线
在确定攻角时,随着起爆半径的增加,阻力系数急剧降低。分析其主要原因是起爆半径增大导致了EFP长径比增大,相应的受力横截面积减小,因此减小了阻力,导致阻力系数降低;在确定起爆半径条件下,随着攻角的增加,其阻力系数会增加。分析其原因是存在攻角时弹丸的迎风面积会显著增大,导致其阻力增大。
3.3 起爆半径和攻角对升力系数的影响
图7展示4种不同起爆半径下的EFP的升力系数随攻角的变化规律。
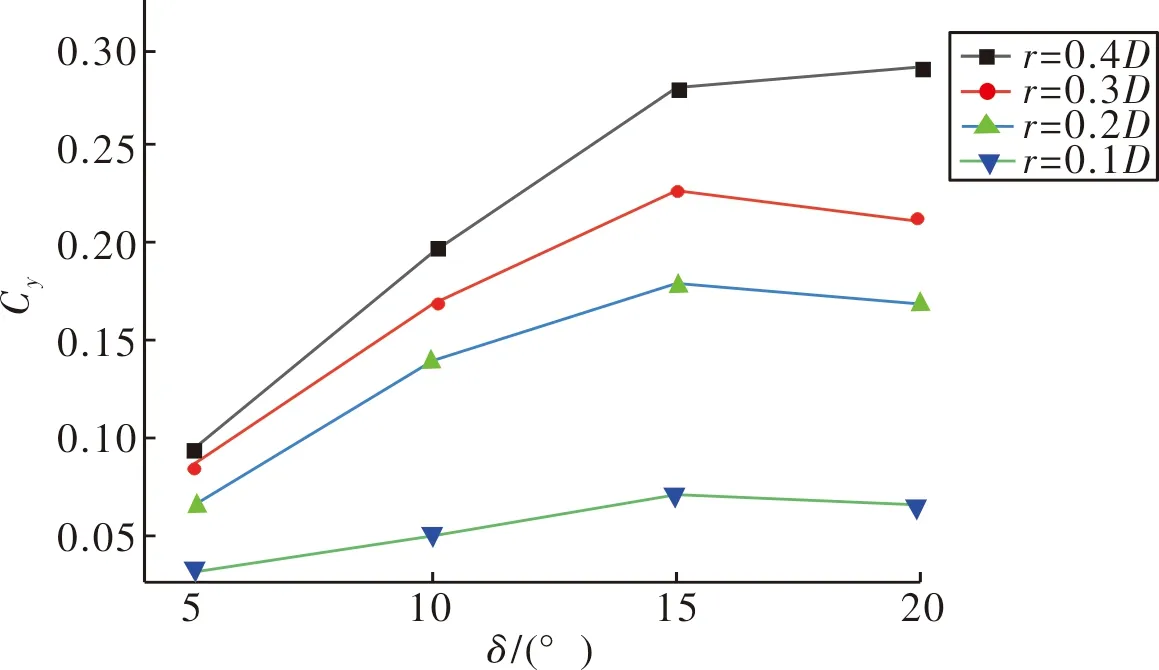
图7 升力系数变化曲线
在确定攻角时,其起爆半径越大,升力系数越大,这是由于起爆半径增大导致弹丸长径比增加,EFP的马赫数更高,作用在弹丸外表面迎风侧和被风侧的气压差值更大,所以其造成的升力更大,而其弹丸最大横截面积却随着起爆半径的增大而减小。因此升力系数会随着起爆半径的增加而增加;起爆半径相同时,随着攻角δ的增加,EFP升力系数呈线性增加,其斜率与起爆半径呈正相关,攻角δ>15°以后,其升力系数增加速度减缓,甚至随着攻角的增加其升力系数开始下降。
3.4 起爆半径和攻角对稳定储备量的影响
稳定储备量是描述尾翼稳定弹丸飞行稳定性的一个重要参量。图8展示了各侵彻体的稳定储备量随攻角的变化曲线。
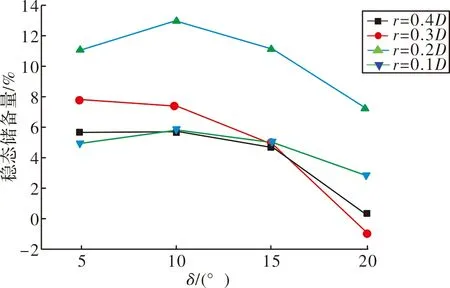
图8 稳定储备量变化曲线
在δ<15°时,随着起爆半径的增加,稳定储备量会有一个先上升后下降的趋势,稳定储备量对攻角的变化不太敏感;在δ>15°时,稳定储备量会急剧下降,弹丸飞行稳定性会明显降低,这会对弹丸的着靶姿态产生不利影响,从而影响弹丸的终点效应。因此尾翼稳定飞行EFP的攻角应该严格的控制在一个合理范围内。
3.5 EFP威力特性综合分析
影响EFP威力的主要因素有长径比、气动特性、速度及速度保存能力。由以上分析可知,在几种不同起爆半径下EFP的速度随起爆半径的增加而增大,且其增长率逐渐减小,尤其是起爆半径r=0.4D与r=0.3D相比,其速度增加仅为0.4%,因此当起爆半径增加到0.3D以上时,仅仅增加的是EFP的长径比,而对EFP的速度增益并不明显。EFP威力重要评价指标之一是开孔直径。因此长径比不宜过大。然而长径比越大,其速度保存能力就越强,但其静态储备量会下降从而影响弹丸的飞行稳定性,静态储备量与阻力系数及弹丸速度这几个因素相互制约,因此应该对其综合考虑。从前面的分析可以看出,起爆半径r位于0.2D~0.3D之间时,EFP的静稳定储备最大,而其阻力系数及EFP的速度都控制在一个较为理想的范围内。
4 结论
采用LS-DYNA对不同起爆半径下的EFP进行数值模拟,并通过Fluent分别计算不同攻角时的阻力系数、升力系数、静稳定储备量等气动参数,得出如下结论:
1)通过UG逆向建模将LS-DYNA计算得到的EFP外形数据传递给流体力学计算软件Fluent进行超高音速气动分析,实现了LS-DYNA与Fluent的联合仿真。
2)通过Fluent气动分析,综合考虑阻力系数、稳定储备量及弹丸速度,确定了成型弹丸6点起爆,起爆半径r位于0.2D~0.3D内时能够获取更好实现其终点效应的侵彻体。

