基于二维空变运动补偿的机动平台大斜视SAR稀疏自聚焦方法

李 根 马彦恒 熊旭颖

(陆军工程大学石家庄校区无人机工程系 石家庄 050003)

1 引言

机动平台大斜视合成孔径雷达(Synthetic Aperture Radar, SAR)成像系统能够进一步增强导弹、战机以及无人机的战场侦察、精确打击和自我生存能力，相关的成像方法受到了广泛关注[1–4]。

机载SAR易受气流扰动，由于惯导设备精度有限，基于回波数据的自聚焦方法通常是SAR成像过程中必不可少的环节。对于机动平台大斜视SAR成像，大斜视角和空间3维加速度的存在使运动误差具有明显的2维空变性，极大地增加了自聚焦的难度。常规的相位梯度自聚焦(Phase Gradient Autofocus,PGA)[5]、最小熵(Minimum Entropy Analysis,MEA)[6]等自聚焦方法及其改进算法[7,8]，在非空变的包络误差校正和方位相位补偿等方面有显著效果。当运动误差同时存在距离和方位2维空变时，文献[9]推导了混合坐标系下图像域和方位时域相位的近似傅里叶变换关系，采用高斯拟牛顿的方法估计3维的运动误差轨迹，并采用时域算法进行成像处理。文献[10]在快速分解后向投影(Fast Factorized Back Projection, FFBP)算法框架下，基于最大对比度准则对双基地SAR成像模式下的双机3维运动误差轨迹进行迭代估计。文献[11]在稀疏自聚焦框架下，提出了一种误差轨迹重建方法，但该方法需要在时域建立稀疏表示矩阵，内存占用极大，仅能用于小场景成像。为实现大场景成像，文献[12]将近似观测算子模型引入稀疏自聚焦框架，极大地降低了内存占用，使稀疏自聚焦方法可以用于大场景成像，但其无法估计和补偿2维空变的运动误差。文献[13]在近似观测算子模型下进一步扩展了稀疏自聚焦框架，提出了一种运动误差幅相联合补偿算法，能够实现空变运动误差的估计与补偿，但巨大的运算量限制了其应用。3维运动误差轨迹的估计需要建立图像域和方位时域相位历程的映射关系，当平台存在较大的斜视角和加速度时，运动误差中的线性分量将极大地影响3维运动误差的估计精度。

常规的PGA和MEA等自聚焦方法仅能用于全采样数据下的误差相位估计和补偿，而稀疏自聚焦方法可以同时用于全采样和欠采样数据下的误差相位估计与补偿，具有更高的精度和更大的适用范围[14]。本文在稀疏自聚焦框架下，提出了适用于机动平台大斜视SAR聚束成像的2维空变运动误差估计与补偿方法。该方法基于Keystone变换和频域相位滤波法[15,16]构建了一种能够校正成像参数空变性的频域近似观测算子，并对距离方位解耦后的方位时域运动误差进行高阶多项式建模，通过多个子区域的非空变误差相位估计空变的运动误差多项式系数，最后通过修正频域近似观测算子中的相位滤波系数，实现了全采样和欠采样数据下的2维空变运动误差的补偿。

本文的后续结构安排如下：第2节介绍机动平台大斜视SAR频域近似观测算子构造方法；第3 节详细论述距离和方位2维空变相位误差的估计与补偿方法，并进行运算量分析；第4节给出真实SAR场景回波反演数据的成像结果，验证了本文方法的有效性；第5节对全文进行总结。

2 近似观测模型

加速度和大斜视角的存在使机动平台大斜视SAR的成像参数具有明显2维空变性，为实现距离方位解耦、多普勒谱去混叠以及空变线性距离徙动的校正，采用文献[4]中的方法对回波信号先后进行距离走动校正、去加速度处理和方位向Keystone变换，可得距离徙动校正和距离压缩后的信号为

在方位压缩处理中，本文基于频域相位滤波[15,16]的思想校正空变的多普勒参数。首先，采用式(4)去除距离依赖的多普勒中心

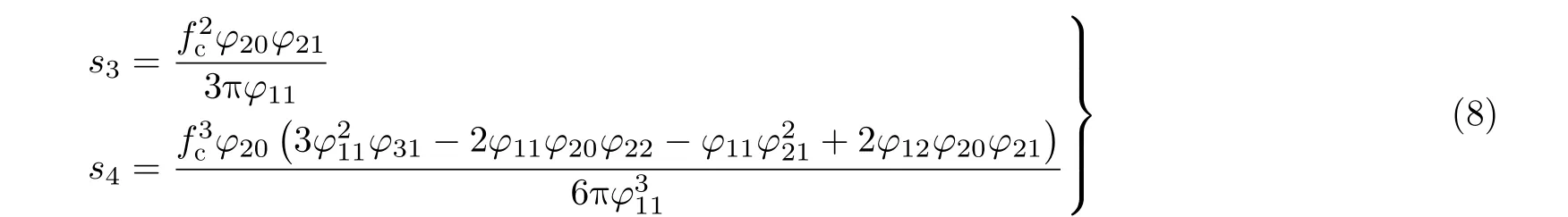
频域相位滤波后，构造如式(9)所示的方位时域Deramp函数

3 2维空变相位误差的估计与补偿

3.1 基于近似观测的稀疏自聚焦方法

式(14)中的稀疏优化模型可以采用基于两步优化和迭代软阈值(Iterative Shrinkage-Thresholding Algorithm, ISTA)的稀疏自聚焦方法[12]进行求解。

3.2 空变的运动误差模型

在距离向处理中，Keystone变换去除了包络幅度误差中线性分量对距离徙动校正的影响，通常情况下，残余的非线性包络幅度误差对距离徙动校正的影响可以忽略。本文重点研究方位压缩过程中，距离空变和方位空变的相位误差估计与校正。

本文采用的2维空变误差校正方法，是通过修正所构建的频域近似观测算子中的滤波系数来实现的。在所构建的频域近似观测算子中，斜距模型为文献[4]中的4阶多项式模型，观察式(3)中多普勒参数的空变展开系数可以发现，在频域相位滤波法中，回波的方位时域调制相位需考虑多普勒中心和调频率的2阶方位空变性，3阶多普勒参数的1阶方位空变性。为便于在频域相位滤波法中校正空变的运动误差，运动误差的多项式阶数应与斜距模型一致。因此，本文将距离压缩回波中的残余空变误差相位在距离和方位向近似为如下所示的4阶多项式模型

3.3 空变误差相位的求解与补偿

假设在Gc中共截取了D个子区域，其中第i个子区域的局部误差相位表示为ϕsub_i。采用最小二乘法可以对其进行多项式拟合，则子区域i的4阶多项式拟合系数表示为

最终，所提机动平台大斜视SAR稀疏自聚焦方法流程如图2所示。由于所提方法采用稀疏自聚焦方法对运动误差进行估计，因此该方法可用于全采样数据下的匹配滤波成像以及欠采样数据下的稀疏成像。

图2 机动平台大斜视SAR稀疏自聚焦方法流程

3.4 算法的场景适用性分析

本文所提稀疏自聚焦方法对成像场景的适用性分析如下：

场景类型的要求：所提方法需要在成像场景的不同区域内选择若干子区域，采用稀疏自聚焦方法进行局部非空变相位误差的估计，要求成像场景具有一定的对比度。PGA通常要求场景中具有强散射点，MEA等图像准则自聚焦方法要求场景具有一定的对比度，所提方法对场景类型的要求与MEA相似，低于PGA。

场景大小的要求：对于机动平台大斜视SAR成像，非线性轨迹和大斜视角的存在使成像参数具有较强的空变性，本文采用Keystone变换和频域相位滤波法进行成像参数空变性的校正，运动误差产生的空变相位误差的校正通过修正频域相位滤波法的时频域滤波系数实现。由于运动误差的幅度远小于平台机动所造成的轨迹偏移，因此成像场景的大小主要由频域相位滤波法的空变性校正能力决定，在频域相位滤波法的有效成像区域内，所提的空变运动误差补偿方法均是有效的。

3.5 运算量分析

本文基于Keystone变换和频域相位滤波法构造了如图1所示的机动平台大斜视SAR频域成像算法。在采用稀疏自聚焦方法估计全局非空变相位误差时，在所有的距离单元中仅需选取平均能量排序前5%～10%的距离单元即可取得理想的效果，这样可以极大地降低矩阵维度，提高算法效率。在对相位误差进行估计时，所提方法仅利用了距离压缩回波Src及相应的频域算子Γ-1(·)和Γ(·)。频域算子共包含3次方位向FFT/IFFT运算和两次矩阵点乘运算，设其运算量为CΓ。

图1 机动平台大斜SAR频域成像处理流程

设稀疏自聚焦的迭代次数为Imax，每次迭代需要计算2次频域算子Γ-1(·)或Γ(·)。在图2的空变运动误差估计过程中，设估计全局非空变运动误差时选用的距离单元占全部距离单元的比例为η1，估计子图像相位误差时，每个子图像的距离单元占全部距离单元的比例为η2，则空变运动误差估计所需的运算量为

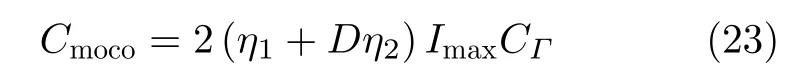
仿真实验表明，Imax＝30,η1＝0.1,η2＝0.02,D＝8即可高精度地估计空变的运动误差，所需的运算量为15.6CΓ。在图2中，实现方位压缩的成像算子Γ(·)的运算量约占整个算法运算量的1/4，因此所提方法进行空变运动误差估计的运算量约为15.6/4 ＝3.9次频域匹配滤波成像的运算量，在SAR稀疏成像中仅相当于2次迭代的运算量，具有较高的运算效率。

4 仿真分析

机动平台大斜视SAR的实测数据还难以获取，本节采用文献[17]的方法模拟真实SAR场景的回波数据验证所提方法的有效性。仿真采用的SAR系统和平台运动参数如表1所示，选择含有少量强散射点且稀疏性较低的场景1用于全采样数据成像实验，含有大量强散射点且稀疏性较高的场景2用于稀疏数据成像实验，场景1和场景2均平行于X轴放置，分别如图3(a)和图3(b)所示。根据常规机载SAR的惯导数据，加入如图3(c)所示的3维运动误差。

图3 仿真场景和3维运动误差曲线

表1 仿真参数

为验证本文所提2维空变相位误差估计与校正方法的有效性，图4给出了全采样数据下场景1的匹配滤波成像结果，同时选择加权PGA(Weighted PGA, WPGA)[7]和基于近似观测的稀疏自聚焦方法[12]作为对比算法，图4中矩形框所选择的子区域为本文方法估计空变相位误差时所选择的子区域。从图4中可以看出，由于WPGA方法对强散射点的依赖较强，对于强散射点较少且对比度较低的场景1, WPGA方法无法有效聚焦；稀疏自聚焦方法[12]能够明显提高聚焦质量，但依旧存在一定的散焦情况，而本文方法具有最好的聚焦效果。

为直观体现本文方法的空变误差校正效果，图5放大显示了图4中部分子区域成像结果，子区域序号对应的子区域与图4中的标号一致。由于 WPGA方法的聚焦效果明显差于另两种方法，因此图5未展示WPGA方法聚焦后的子区域成像结果。从图5中可以看出，稀疏自聚焦方法可以估计全局的非空变误差相位，但残余的空变误差相位降低了局部子区域的聚焦质量，本文方法同时估计了距离和方位向的空变多普勒系数，能够校正子区域的空变相位误差，对场景1中不同的子区域均有较好的聚焦效果。为进一步量化分析所提方法的聚焦效果，采用图像熵和对比度量化分析图4中3种方法的聚焦效果，结果如表2所示。可以看出，本文方法聚焦图像的熵值最小，对比度最高，具有最好的聚焦效果。

图4 全采样数据下的场景1成像结果对比

图5 场景1局部区域成像结果

表2 场景1成像结果量化分析结果

为验证本文方法的稀疏成像效果，抽取场景2的36%原始回波数据进行成像处理，其中稀疏采样矩阵L中的降采样率ξa和ξr均为0.6，场景2的成像结果如图6所示，其中WPGA、稀疏自聚焦和本文方法聚焦图像的熵值分别为15.50,12.06和11.95。从图6中可以看出，距离和方位向的欠采样使基于WPGA的匹配滤波方法的成像结果存在严重的欠采样噪声，本文方法和稀疏自聚焦方法均可以有效去除这种欠采样噪声，同时由于本文方法校正了空变的相位误差，具有更小的熵值和更好的稀疏成像效果。

图6 欠采样数据下的场景2成像结果对比

5 结束语

本文提出了一种适用于聚束式机动平台大斜视SAR的空变运动误差估计与补偿方法，该方法结合Keystone变换和频域相位滤波法构造了近似观测算子，并采用基于近似观测的稀疏自聚焦方法估计全局非空变和局部空变的误差相位。所提方法仅抽取少部分距离单元进行全局非空变相位误差的估计，具有较高的运算效率，能够用于全采样和欠采样数据下的自聚焦处理，仿真实验验证了所提方法的有效性。受限于频域相位滤波法的多普勒参数空变校正能力，本文方法仅适用于低阶的空变运动误差，下一步将研究高阶空变运动误差下的稀疏自聚焦方法。