基于深度生成对抗网络的海杂波数据增强方法

丁 斌 夏 雪 梁雪峰

①(西安文理学院 西安 710065)

②(西安石油大学 西安 710065)

③(西安电子科技大学 西安 710071)

1 引 言

随着我国建设海洋强国战略的全面实施，海洋生态文明建设作为生态文明建设的重要组成部分，已成为国家战略。海洋遥感作为监测和感知海洋环境现状，保障海洋生态文明建设和海洋经济绿色发展的重要技术手段，越来越被研究人员所关注。雷达作为海洋遥感的主动式传感器之一，发挥着不可替代的作用。

雷达回波中的海杂波会严重影响雷达目标检测，尤其是在复杂的海洋环境中，由于海面风力、海面环境湿度、浪涌等多种自然因素的影响，雷达海面回波在雷达接收机中出现严重的多径效应，导致海杂波信号相比其他信号变化复杂、强度高。因此，海杂波特性及建模研究是一个探索性强且难度很大的瓶颈技术问题，也是当前雷达海洋目标检测研究的难点和热点问题。

众所周知，不论是雷达海洋目标探测还是海杂波特性及建模研究，都离不开海杂波数据的支持。目前，海杂波数据的获取方法主要可归纳为两类，一类是基于雷达-海面目标几何模型和电磁散射理论，通过仿真建模生成海杂波数据；另一类是进行试验，获取实测海杂波数据。

理论建模可以通过数值计算获得实际测量难以得到的特性数据；而实测数据又为理论建模提供了有效的验证依据。然而，实际海洋环境复杂，海面目标的散射起伏不定，海杂波呈现非高斯、非线性和非平稳特性，很难使用某种确定不变的统计分布模型来对实际场景中的海杂波进行描述和建模。

随着海洋遥感监测的需求越来越多，要求越来越高，同时，雷达的工作模式及其参数、雷达探测环境都是复杂多变的，因此需要大量的海杂波数据以支撑更加准确的海杂波特性的分析。

由公开文献可知，世界各国对海杂波数据的获取非常重视，而且进行了大量的海杂波测量试验[1]。国外方面，主要有美国海军研究实验室的4波段(P,L, C, X)机载雷达海杂波测量实验[2]、美国海军与美国国防部高级研究计划署的“山顶计划[3]”、加拿大麦克马斯特大学的X频段海上冰山监测雷达(Ice multiParameter Imaging X-band radar,IPIX)海杂波测量试验[4,5]、西班牙南海岸Ka频段雷达海杂波测量试验[6]、澳大利亚国防科技署(Defense Science and Technology Organization,DSTO)的L频段多通道海杂波实验[7–9]、南非科学和工业研究理事会(Council for Scientific and Industrial Research，CSIR)的X频段Fynmeet雷达海杂波测量试验[10,11]等。

国内方面，中国科学院空天信息创新研究院、中国电科第14所、第38所等研究所，以及西安电子科技大学、电子科技大学、哈尔滨工业大学、哈尔滨工程大学、南京理工大学、北京理工大学、大连海事大学、国防科技大学、空军预警学院、海军航空大学等高校也开展了多种条件下海杂波测量试验，获取了不同雷达平台下大量海杂波数据，并在海杂波测量、海杂波特性分析建模、多域特征提取等方面开展了大量的研究工作[12]。

尽管如此，当研究人员准备从事海杂波特性研究时，还是不可避免地面临两大困境：一方面，海杂波实测数据的采集需要耗费较长时间和昂贵的资源。另一方面，雷达对海上目标探测研究，需要雷达实测数据支持，由于军事及技术保密等原因，大多数雷达实测海杂波实验获取的数据集均未公开，更加严峻的是，前期已公开的雷达对海探测数据，现在也难以获取。目前在深度学习领域，生成对抗网络(Generative Adversarial Networks, GAN)已成功用于训练数据的数据增强，本文改进了传统GAN网络模型结构，通过网络模型学习真实海杂波数据的分布，生成与真实海杂波数据分布一致的海杂波数据。

2 GAN原理

Goodfellow等人[13]于2014年首次提出GAN，即一种深度对抗生成网络，并且从理论上证明了，当GAN在训练到纳什均衡点(Nash Equilibrium，又称为非合作博弈均衡，是博弈论的一个重要术语，以约翰·纳什命名，在一个博弈过程中，博弈双方的平衡策略都是为了达到自己期望收益的最大值，此时这个平衡策略就定义为纳什均衡)时模型收敛，该生成模型的生成数据的概率分布与真实数据相同。

生成对抗神经网络由两部分组成：生成器网络(Generator, G)和判别器网络(Discriminator, D)。如图1所示，生成器G的输入为从某个概率分布(如高斯分布)中采集的随机变量z，z经过G网络(复杂的非线性变换)后，得到输出信号G(z)，我们将G(z)称为生成数据。

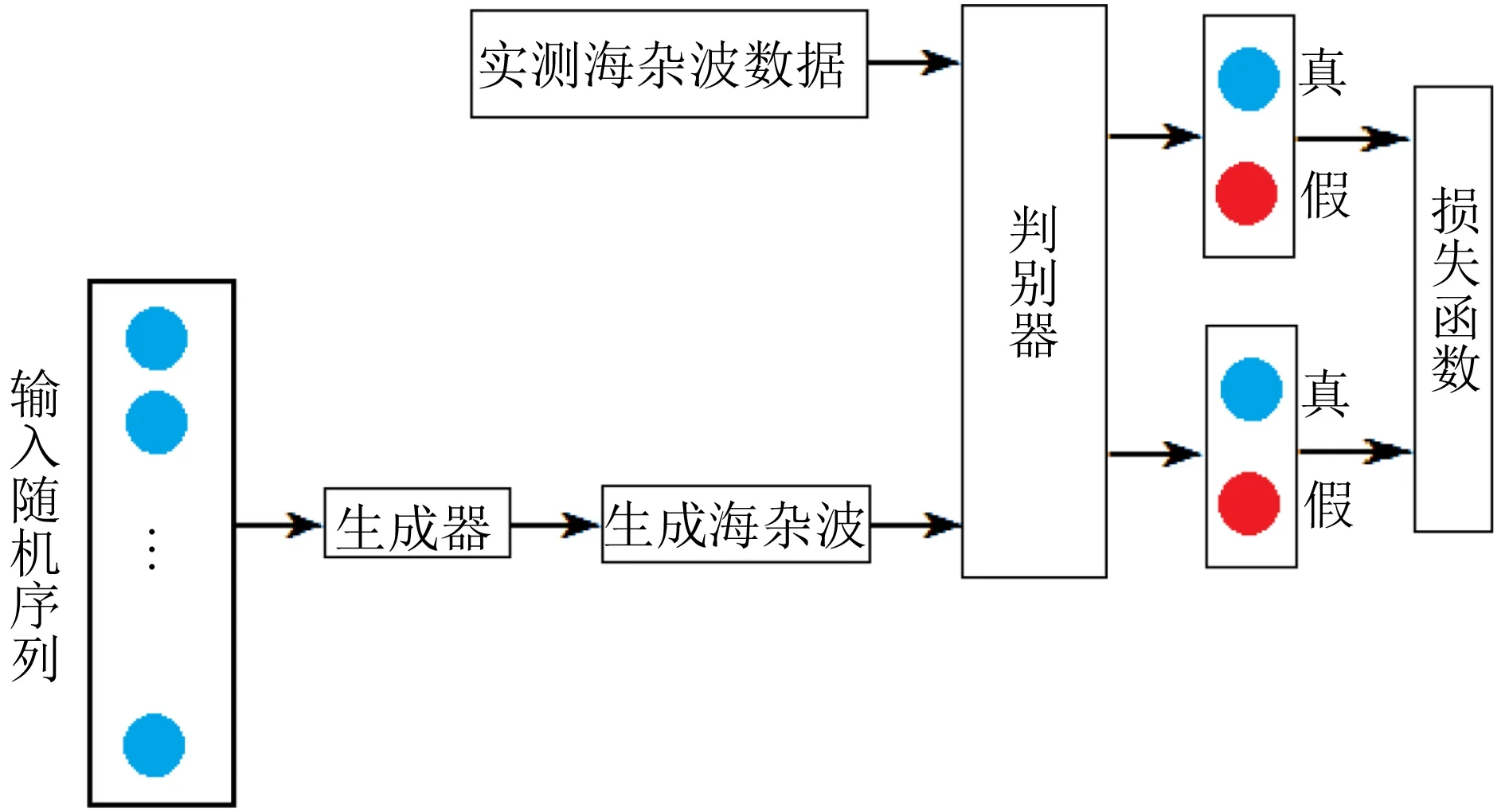
图1 GAN结构示意图

将真实数据x和生成数据G(z)同时输入判别器网络D，判别器通过计算输入数据来自真实数据x的概率，来判断输入数据是来自生成数据G(z)还是真实数据x。当判别器输入信号为生成信号时，判别器输出判别概率尽可能接近0(判别为假)；而生成器尽可能生成同分布高质量的样本使判别概率接近1(判别为真)。当生成器和判别器通过训练，性能足够好时，即生成器生成的数据与真实海杂波数据有相同的分布时，判别器分不清输入数据是真实海杂波数据还是生成数据，判别器对每个输入(不论是来源于x，还是G(z)), 判别概率都等于0.5，即认为达到纳什均衡点[2]。

建立如式(1)所示的损失函数，对两个网络G和D进行对抗训练，G的训练目标是使目标函数最小，即生成数据的概率分布逼近真实数据x的分布；与之相对地，D的训练目标是使目标函数最大，即以最大概率区分生成数据与真实数据

经过交替、迭代训练后，判别器网络D和生成器网络G的网络参数不断更新，性能得到不断提高，当达到纳什均衡点时，判别器D不能对数据源做出正确判断，此时我们认为G(z)学习了真实数据x的分布空间，生成数据和真实数据的分布无差异。

3 海杂波数据对抗生成网络架构

目前的GAN研究直接将实值神经网络应用于图像的幅度(通常转换为dB)，而忽略了相位信息。相位信息是雷达回波数据特有的信息，在许多雷达信号处理中都需要用到回波数据的相位，其中最突出的是脉冲压缩(匹配滤波)。

雷达海杂波数据的数据格式是复数形式，目前公开文献有涉及复数卷积神经网络应用实例，例如用于极化SAR图像分类[14]。复数的确有可能能够增强每个神经元的表达能力，但是神经网络中的每个神经元都是由简单的激活函数构成(都是实数)的，深度神经网络的强大在于它的链接。使用复数神经网络与神经网络的理念相背离。

因此，本文使用两个相同网络结构的GAN网络分别生成海杂波数据的实部和虚部，而后将实部与虚部合成海杂波的复数数据。具体的网络结构如图2所示。

图2 海杂波数据对抗生成网络结构

生成器网络结构包括1个输入模块、5个卷积模块和1个输出模块。其中输入模块包含1个全连接层和ReLU激活函数；卷积模块包含1个上采样层、1个1维卷积层和ReLU激活函数；输出模块包含1个1维全连接层和Tanh激活函数。判别器网络包括5个卷积模块和1个输出模块。其中卷积模块包含1个1维卷积层和1个Leaky ReLU激活函数，输出模块包含1个全连接层和Sigmoid激活函数。

当生成器网络输入长度为100的随机序列时，首先经过输入模块(输入100、输出256的全连接层+ ReLU激活函数)后，输出长度为256的序列，再经过第1个卷积模块，经过2倍上采样后得到长度为512的序列，再经过512通道，卷积核大小为1×3，输入序列左右各补1个0(padding＝1)，卷积步长为1(stride＝1)的1维卷积层，然后通过ReLU激活函数后，得到输出512个通道，长度为512的信号；依次经过第2个、第3个直到第5个卷积模块。最终经过输出模块(全连接层+Tanh激活函数)得到长度为8192的生成信号。

当长度为8192的生成信号输入判别器网络，首先经过第1个卷积模块，模块中的1维卷积层参数为，卷积核个数为64，卷积核大小为1×3, stride＝4，在序列左右各填充两个0，即padding＝2。经过第1个卷积模块后，输入信号尺寸变为64个通道，长度为2048。分别经过第2、第3和第4个卷积模块，输出变为512通道，长度为32。随后经过最后一个卷积模块(卷积核个数为1024，卷积核大小为1×3，stride＝2，在序列左右各填充两个0，即padding＝2)后，输出变为单通道。最后经过全连接层和Sigmoid激活函数判别输入信号为真实信号还是生成信号的概率D(x)。上述网络模块具体参数详见表1。

表1 生成器、辨别器网络参数

4 网络训练

本文中用于训练的实测海杂波数据来源于文献[1]。数据采集时，雷达天线凝视海面某一方位，脉冲发射模式，发射脉冲为单载频信号，发射脉宽40 ns，脉冲重复频率(Pulse Repetition Frequency,PRF)为3 kHz，距离向采样率为60 MHz。该组数据共包含60000帧样本数据，采样时长约为3.33 s，每帧数据包含1320点数(距离向采样点)，海杂波信号时域波形如图3所示。

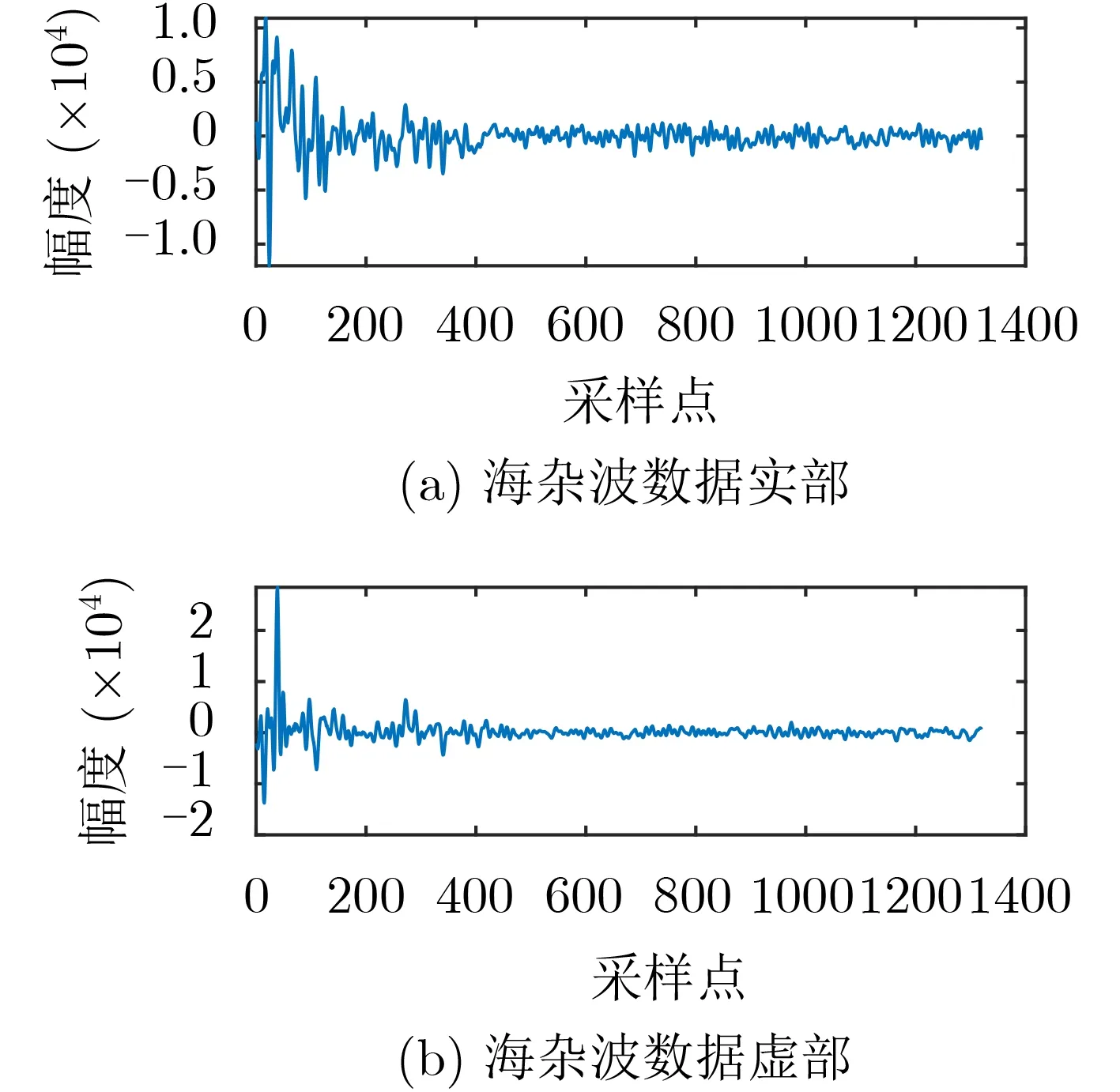
图3 单载频发射信号，海杂波时域波形

网络训练过程如下：

(1)判别器的训练。判别器的训练目标为，当真实海杂波信号输入判别器网络后，网络输出的判别概率越大越好；同时生成器生成的海杂波数据输入判别网络后，网络输出的判别概率越小越好。即判别器能够明确区分输入判别器信号是真实海杂波还是假的。

(2)生成器的训练。生成器的训练目标是使生成器生成的“假的”海杂波数据通过判别器D后的概率越大越好，即式(1)中的第2项越小越好，也就是说生成器生成的数据能够“骗过”判别器。

在整个对抗生成网络的训练过程中，判别器D和生成器G交替进行，开始训练时，先对判别器进行训练5次。

GAN网络在实际训练过程中，尤其是生成网络在训练过程中会出现局部模式崩溃、梯度消失等问题，很难使得生成网络和判别网络同时收敛。为此，Wasserstein生成性对抗网络(Wasserstein Generative Adversarial Networks, W-GAN)[15]在GAN损失函数的基础上增加了梯度惩罚项，如式(2)所示

在对抗生成网络的训练过程中，最重要的影响因素就是学习率参数，学习率直接控制着训练网络梯度更新的量级，直接影响网络模型的有效容限能力。过高的学习率会导致训练过程(损失函数)的震荡，进而出现无法收敛到最优解的情况；过低的学习率会使网络收敛速度变慢，容易陷入局部最优解等问题。在本文实验过程中，我们将学习率参数设置为lr＝0.0005。

其次，网络训练中批样本数量(batch size)的设置，批样本数量决定了训练梯度下降的方向。过小的批数量，极端情况下，例如批处理大小设置为1，即每个样本都去修正1次梯度方向，样本之间的差异越大越难以收敛。若网络中存在批归一化(batch normalization)，批样本数量过小则更难以收敛，甚至垮掉。这是因为数据样本越少，统计量越不具有代表性，噪声也相应地增加。而过大的批样本数量，会使得梯度方向基本稳定，容易陷入局部最优解，降低精度。在本文实验过程中，本文将批样本数量设置为1024，效果较好。

最后，Adam优化器[16]中的β1, β2设为 0.5,0.9。梯度惩罚项权重λ设置为0.6。生成器的潜在变量z从N(0,1)中采样。

5 GAN生成海杂波数据结果与评估

本文用于生成海杂波数据的GAN的实验硬件环境是：NVIDIA 2080 Ti GPU, CUDA 9.1,Ubuntu 16.04、内存32 GB。软件采用TensorFlow 1.4和Python3.6。

实验中使用的训练数据集如图3所示，神经网络训练中的一些参数配置如表1所示。当GAN训练10000 epoch后，生成器网络生成的海杂波数据的实部、虚部分别如图4、图5所示，通过对比可见，生成数据样本与真实海杂波数据的时域波形相近。

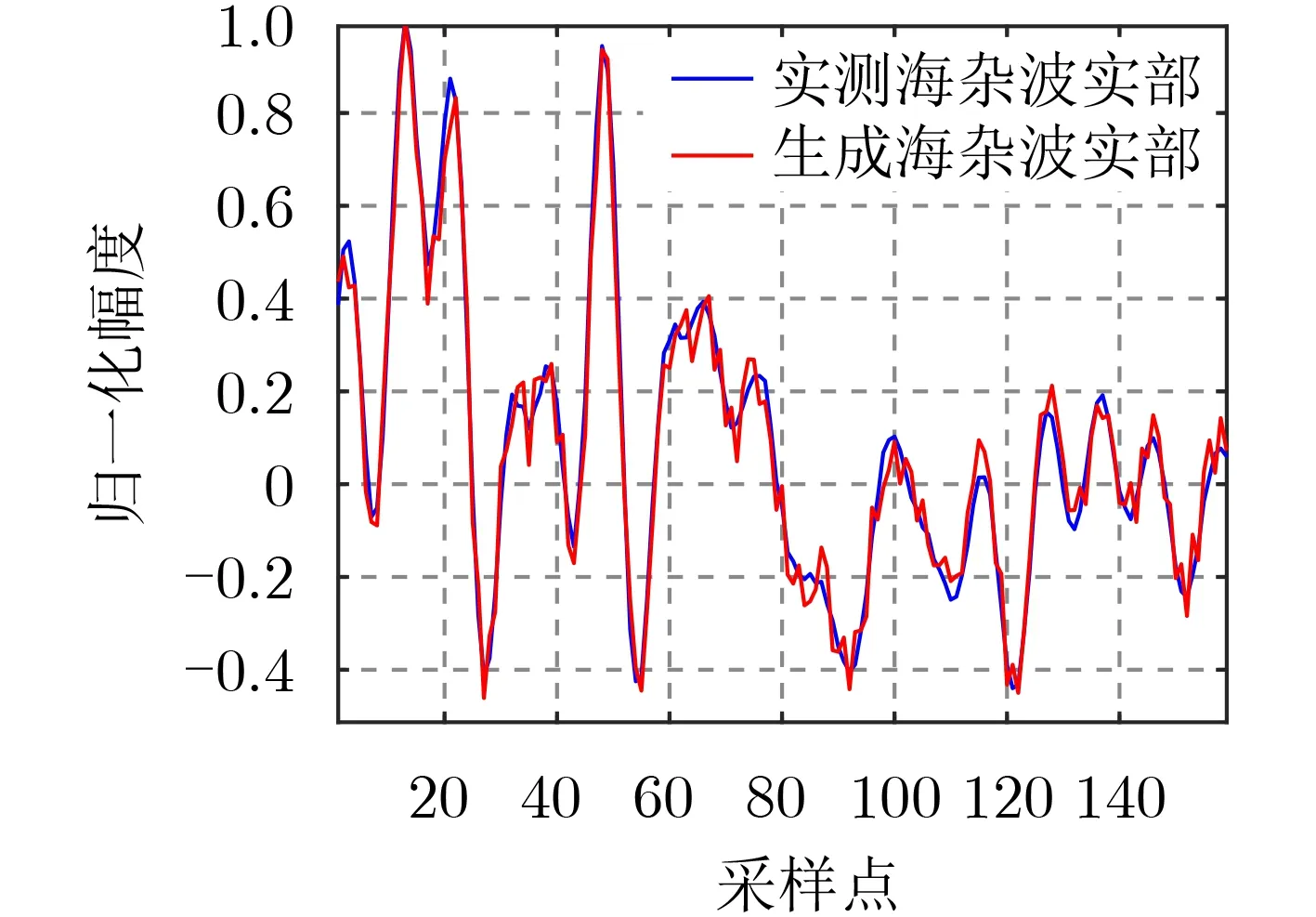
图4 实测海杂波数据实部&生成海杂波数据实部

图5 实测海杂波数据虚部&生成海杂波数据虚部

与确定性信号和图像的生成质量评估不同，由于海杂波是来自雷达分辨率单元中海面的多个散射体回波的矢量和，而且雷达分辨率单元内的散射体是随机分布的，其介电常数和几何特性都是随机变量。同时，海面散射体或雷达平台的相对运动也会引起海杂波幅度和相位的变化。因此一直以来，人们将海杂波看作随机过程。

下面分别从幅度分布特性、时间相关性和空间相关性3个方面对生成的海杂波数据进行评估。

(1)幅度分布特性验证。首先，分别画出距离向第100采样点处，沿时间维(10000帧)的实测海杂波数据和生成海杂波数据的幅度图，分别如图6和图7所示。其次，对同一距离单元的回波幅值进行统计，得出的实测海杂波数据和GAN生成海杂波数据的幅度统计直方图，分别如图8和图9所示。

图6 第100采样点10000帧海杂波幅度

图7 生成海杂波数据(10000帧)杂波幅度图

图8 第100采样点10000帧海杂波幅度直方图

通过对比杂波幅度统计直方图和概率分布拟合曲线，生成海杂波数据与实测海杂波数据的幅度概率分布特性一致，说明利用生成数据的分布可以逼真地模拟海杂波的幅度分布。

直接生成回波幅度(模值)形成的幅度分布统计结果如图10所示。对比图9和图10可知，采用实部虚部分开的方式生成数据幅度分布与直接生成回波幅度(模值)的幅度分布是不一致的。

图9 生成海杂波数据(10000帧)幅度直方图

为了进一步说明本文算法的合理性，将图8、图9和图10的幅度分布拟合曲线示于图11。可见，本文算法生成的数据与实测海杂波数据的幅度分布更加一致。

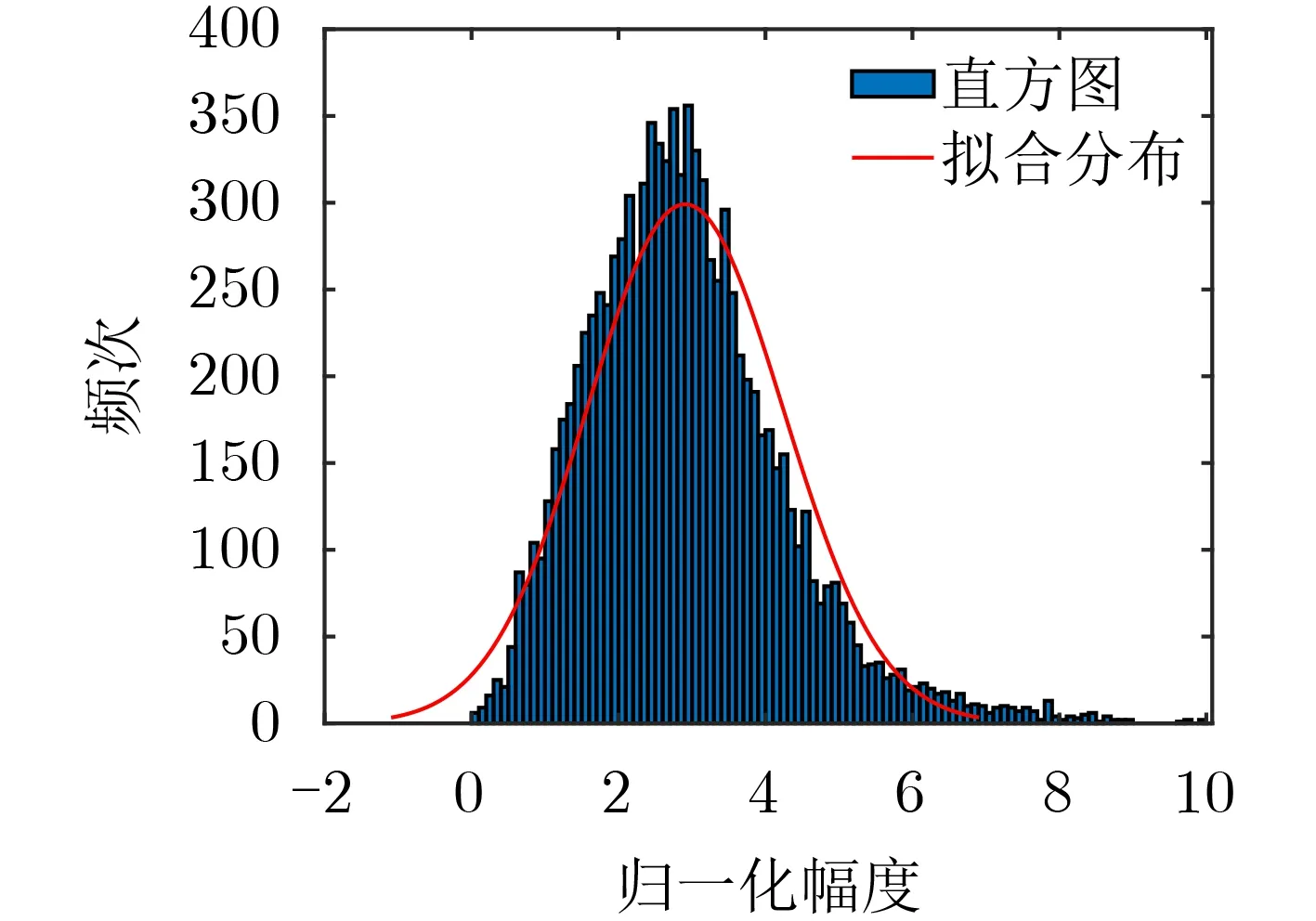
图10 直接生成回波幅度(模值)(10000帧)直方图

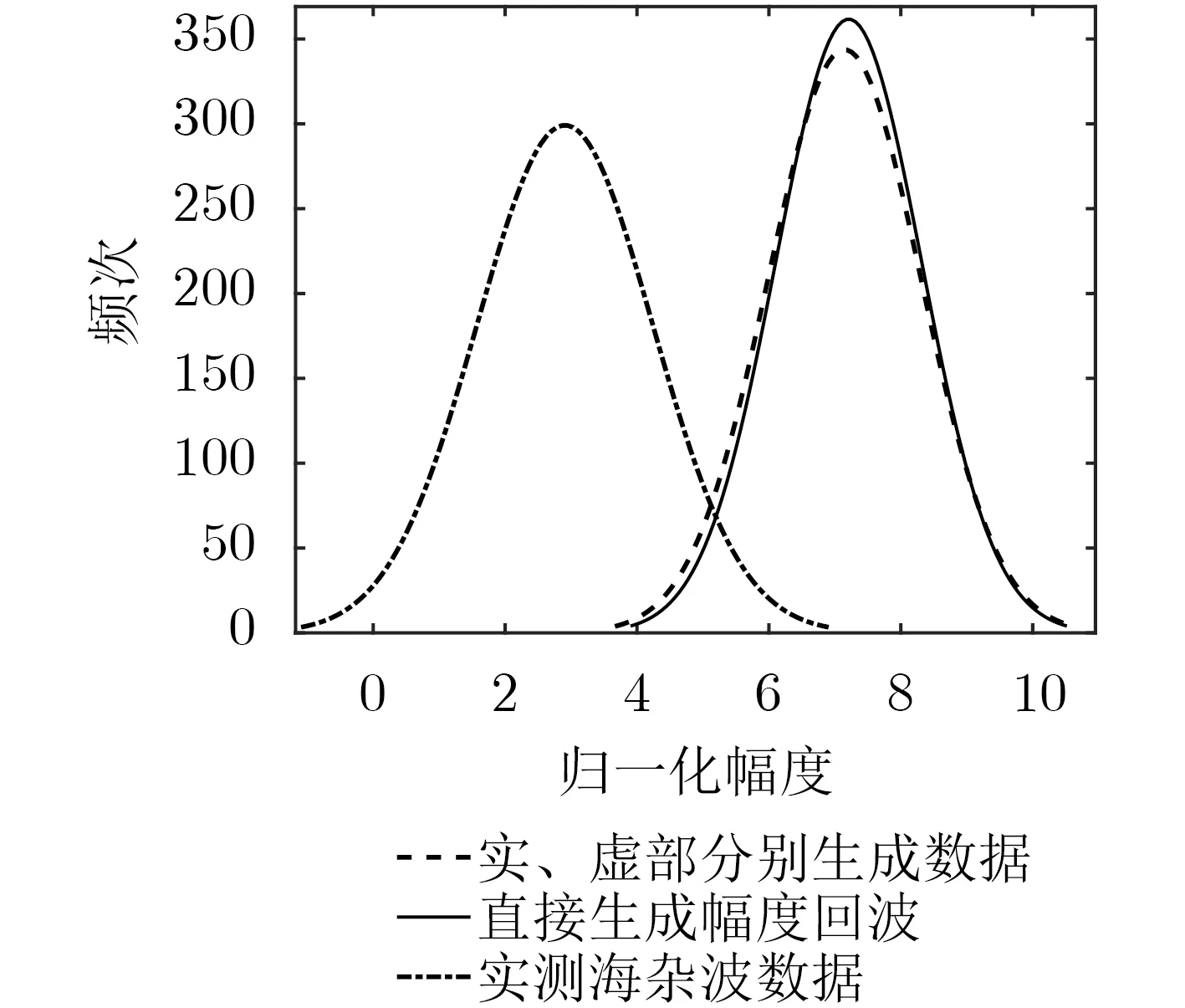
图11 幅度分布拟合曲线

(2)时间相关性验证。下面分别从时间自相关函数和功率谱曲线两个角度，对实测海杂波数据和生成海杂波数据的时间相关特性的一致性进行说明。

图12为利用Burg法分别对生成的海杂波数据和实测海杂波数据进行功率谱估计所得曲线，由于实测海杂波数据是单载频模式下采集的，经过解调后，杂波数据的频谱位于零频附近，由图12可见，在功率谱密度曲线的低频范围，两条曲线拟合较好。

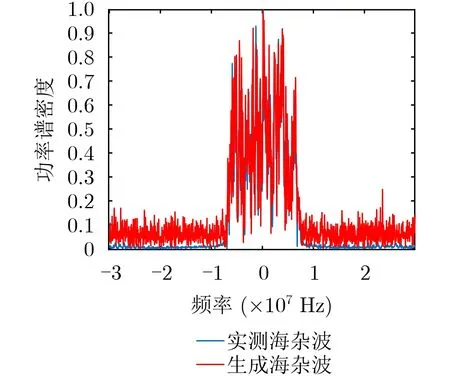
图12 实测海杂波数据&生成海杂波数据功率谱密度

实测海杂波数据和生成海杂波数据的归一化时间自相关函数曲线如图13所示，可见两条曲线几乎重合。综上分析可知，生成海杂波数据可有效地模拟海杂波的时间相关性。

图13 实测&生成海杂波数据时间相关系数

(3)空间相关性验证。

通过式(3)分别计算实测海杂波数据和生成数据的空间相关系数，如图14所示。

从图14可知，实测海杂波在距离向空间相关性首先在初始点处会出现一个尖峰，在经历一个快速的下降期以后出现一个缓慢的周期性衰减，随后距离向的海杂波数据不再相关，此时对应的距离间隔称为海杂波的相关长度。利用GAN生成的海杂波数据的距离空间相关系数同实测海杂波数据的空间相关性相似。

图14 实测海杂波&生成海杂波距离向第100采样点处距离维空间相关系数

6 结论

本文将深度生成性对抗网络应用于海杂波数据生成，通过扩展GAN网络，将GAN应用于一维海杂波复数据的生成，验证了利用GAN生成海杂波数据的可行性，基于实测数据集进行一维海杂波数据生成模型和鉴别模型的训练，并从幅度特性、频谱特性和时空相关特性分析了生成数据质量。最后，比较了实部虚部分开生成海杂波和直接生成海杂波幅度(模值)两种方式的海杂波幅度统计结果。结果表明本文方法能够有效地生成更多、更多样、与真实海杂波数据分布相近的海杂波数据。