一种基于峰度系数的脉冲噪声检测算法的研究及其FPGA实现

周晓波 王 洪* 周郭飞

①(北京交通大学电子信息工程学院 北京 100044)

②(公安部第一研究所 北京 100048)

1 引言

激光在投射到被测物体上时，物体的振动使激光产生多普勒效应，这是激光测振技术的理论基础。在实际应用中，多普勒激光测振系统往往工作在非理想环境下，例如粗糙的物体表面、激光光学元器件的非理想性以及环境噪声等，多普勒激光信号会产生散斑效应，信号出现失真，给解调系统带来了不确定性。这种不确定性会导致解调信号中出现脉冲噪声等问题。这种情况下，线性系统和2阶统计特性对于这种非高斯非平稳信号的处理存在着局限性，需要更高阶的统计特性来描述。高阶统计特性，意味着更复杂的数学运算。随着计算机技术的技术革新，复杂的数学运算不再是高阶统计量在工程中应用的桎梏[1]，高阶统计量的应用范围越来越广泛。

高阶统计特性作为一种特征参数应用在信号分类器中，能够提高系统的抗噪性能[2]。近年来，基于高阶累积量的峰度检测则广泛应用于各个领域：激光系统中微弱脉冲检测[3]、机械系统故障检测[4–6]、电磁应用[7]、医学脑电图特征诊断[8]、语音信号增强[9–12]等方面。国内外利用高阶累积量对语音信号进行研究，主要应用在静音检测[9]、功率谱峰度检测[10]、语音端点检测[11]、音乐质量评估[12,13]等方面。本文对基于高阶累积量的峰度检测算法检测脉冲噪声的可行性进行了理论研究，推导了峰度系数的精确数学迭代公式。为了在FPGA中实现脉冲噪声的实时检测，进一步简化了迭代公式，并提出了一种动态阈值的判决方法，合理地对计算量进行了优化。本文的结构如下：第2节理论阐述高阶累积量的峰度检测算法；第3节对语音的4阶累积量进行研究；第4节推导迭代算法的精确公式；第5节利用MATLAB对算法进行仿真验证；第6节详述FPGA的优化和实现过程；第7节为结论。

2 基于4阶累积量的峰度检测算法

高阶累积量可以自动抑制加性高斯噪声。因此，非高斯的信号，如脉冲噪声，可以利用高阶累积量来对它的统计特性进行描述。

将ψ(ω)展开成泰勒级数

对于0均值的高斯随机过程，其高阶(3阶及以上)累积量等于0，换言之，高阶累积量对0均值高斯信号是“盲”的。即对于0均值的随机过程，可以将4阶累积量的计算进行简化，近似估计为

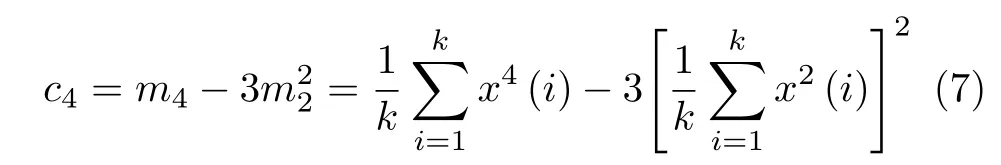
式(7)由4阶矩和2阶矩计算而来，反映了随机变量在其均值附近的尖锐程度，定义为随机信号的峰度。其归一化的4阶累积量为

3 稳定语音信号的4阶累积量特性

在语音信号处理中，一般是应用高阶统计量固有的高斯抑制和相位保持特性对信号进行处理[14,15]。

根据语音的正弦模型，语音信号是由若干正弦波的叠加，通过带状的对角切片部分可以表达语音的振幅和频率。使用连续时间序列表示成

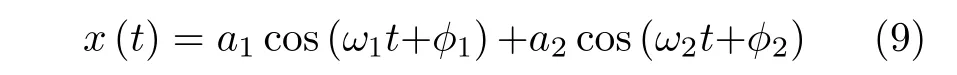
使用该模型对语音信号的4阶累积量进行研究，其峰度系数为

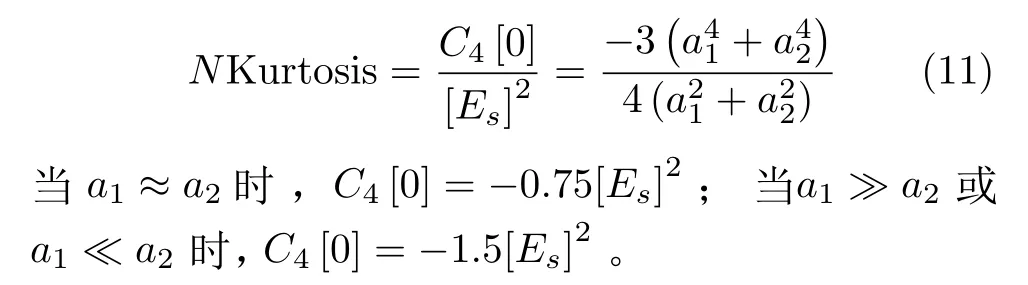
理论上可以确定语音信号的归一化的峰度系数为–1.5～–0.75。若存在脉冲噪声，其非高斯的特性会使得归一化峰度系数高于0。因此，通过阈值判定的方法，能实现在语音信号中将脉冲噪声检测出来。

4 峰度检测算法的迭代公式推导

高阶累积量的计算复杂，运算量极大。在工程应用中，为了能够在FPGA中实现峰度系数的计算，需要利用合理的数学推导和优化对计算公式进行简化。采用数学迭代[16]的方式，能够降低计算复杂度。以下推导了精确的迭代公式，并根据语音信号的特性，进行了一些简化，得到改进的峰度系数迭代公式

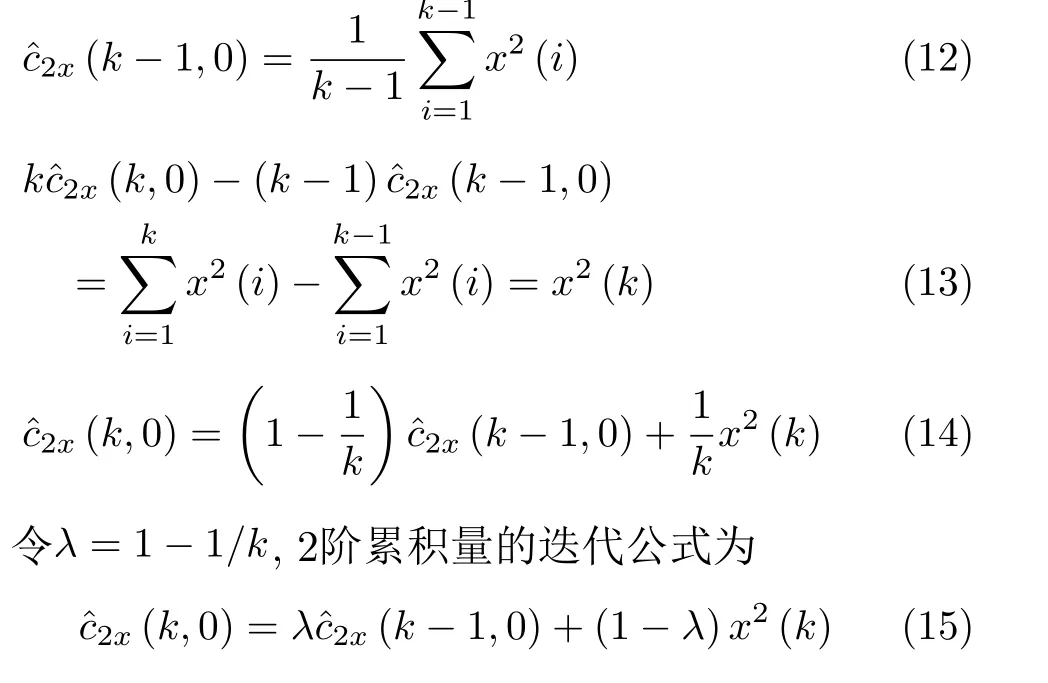
2阶累积量可以用作信号的能量检测

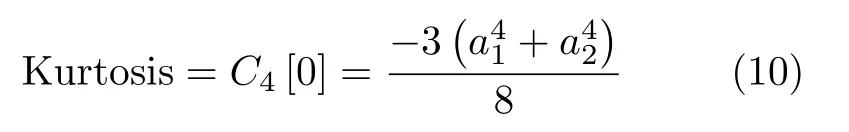
归一化峰度系数

当k足够大时，k+2≈k，化简后

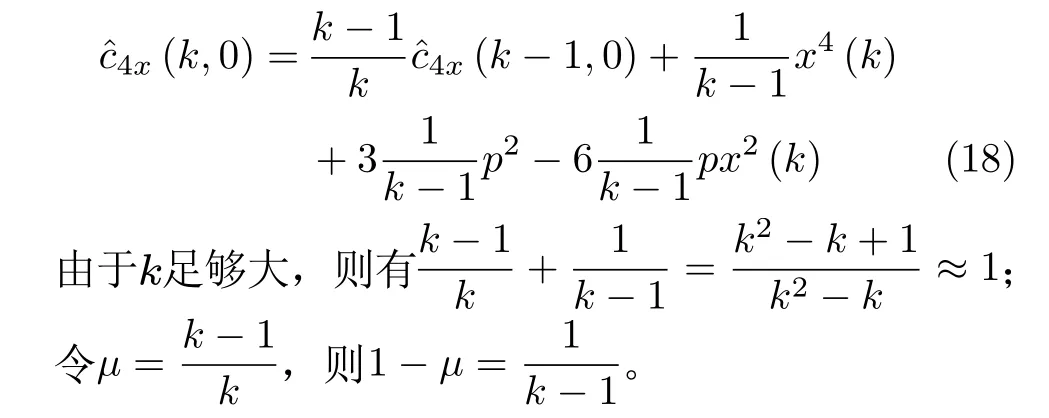
4阶累积量的迭代公式化简为

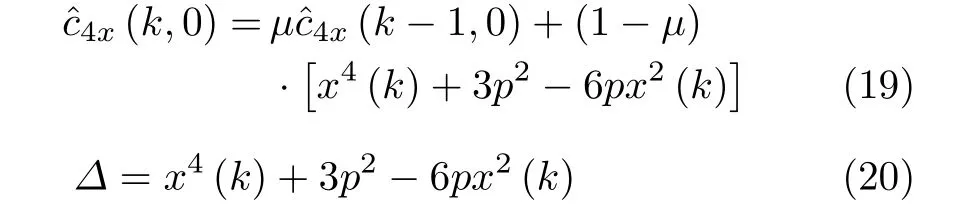
Δ为4阶累积量的迭代运算的更新因子。

对于语音信号，可以近似认为：p ≈x2(k)，则有

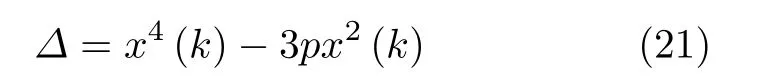
同4阶累积量的推导过程，推导出改进的归一化4阶累积量的迭代公式为

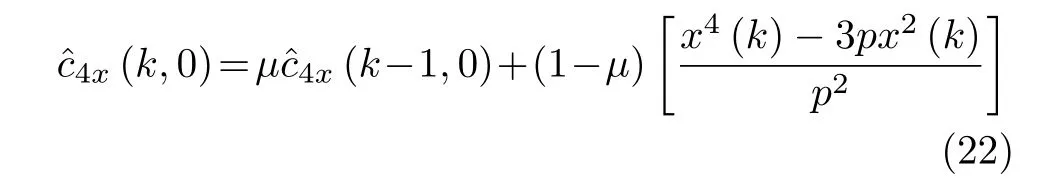
改进的归一化更新因子(近似)

5 MATLAB仿真

利用MATLAB对峰度系数迭代算法进行仿真，仿真数据为真实采集的带有脉冲噪声的低信噪比语音信号。仿真对比了改进的峰度系数迭代公式和初始迭代公式的检测性能以及不同参数下的归一化峰度系数的检测性能。由图1可看出，在语音脉冲噪声检测的应用下，改进的峰度系数迭代算法具有更大的峰度值，而且在脉冲噪声幅度较小时，表现出了更敏感的特性，有利于语音脉冲噪声的检测。

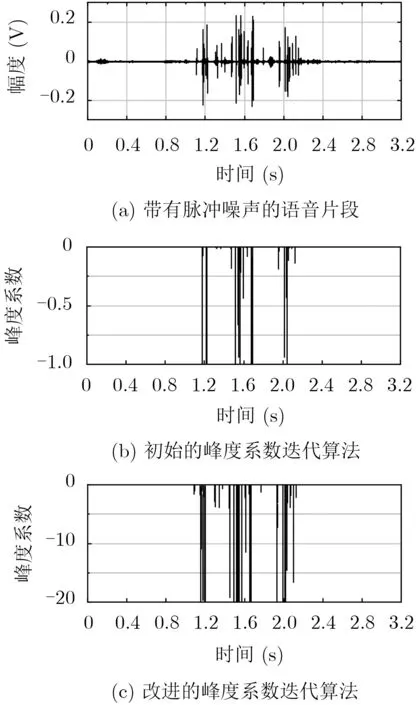
图1 改进的峰度系数迭代算法与初始迭代算法的性能比较(μ＝0.9, λ＝0.9)

通过调整迭代公式中的遗忘因子μ，对归一化峰度系数进行仿真对比。由图2，遗忘因子μ越小，对于脉冲噪声就会越敏感。而对于正常的语音信号来说，归一化峰度系数值总是小于0的。

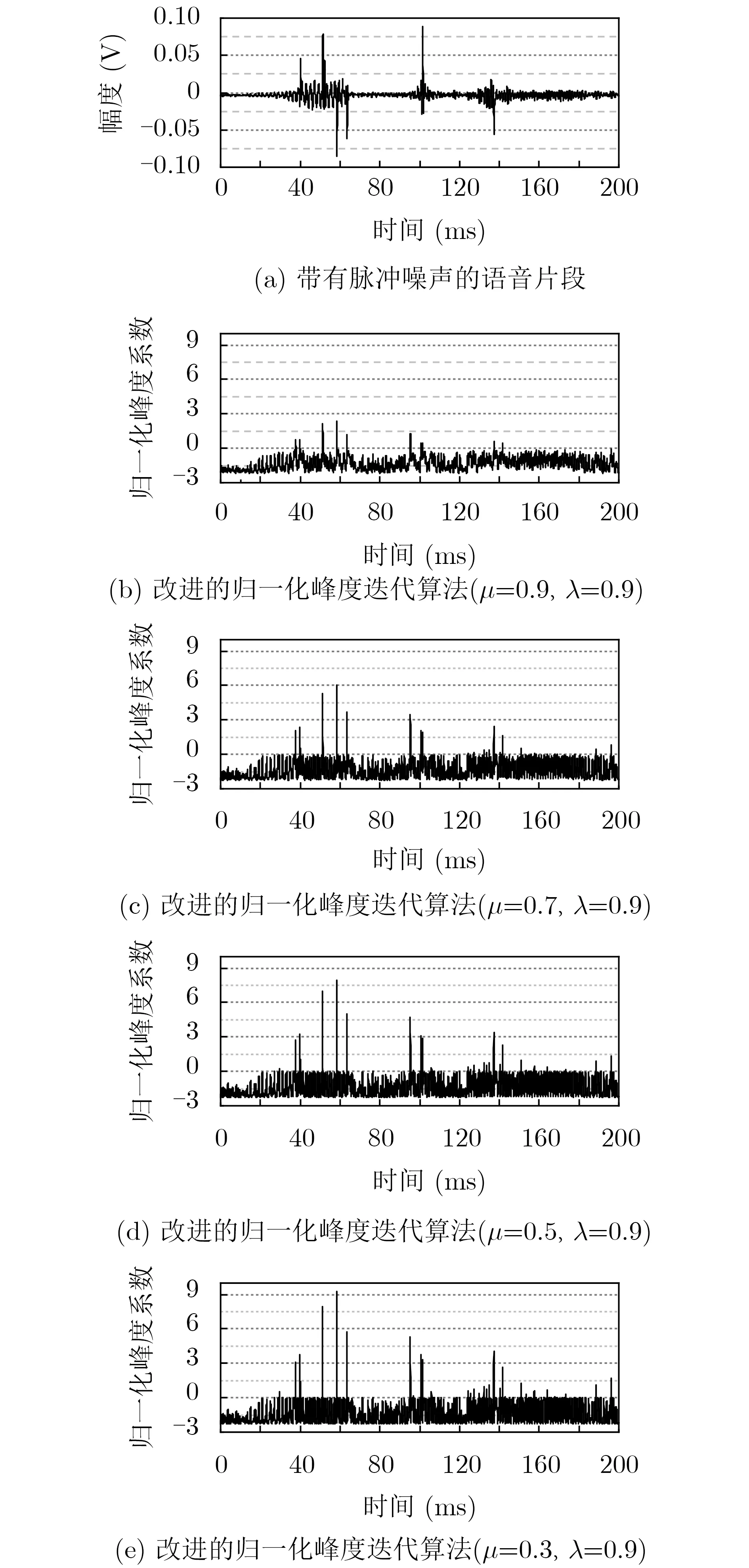
图2 μ值对峰度系数的影响

6 FPGA设计与实现

使用FPGA进行数字电路设计，FPGA是定点数的运算方式，其并行运算的特点能够以更少的硬件资源实现更快速的运算，从而满足实时性的需求。以MATLAB的浮点数的模型作为参考，改进的峰度系数的迭代公式和动态阈值的判决方法在FPGA里的结构图由图3所示，包含峰度系数计算和动态阈值计算两个模块。系统时钟采用49.152 MHz，输入解调语音信号的采样频率为32 kHz。

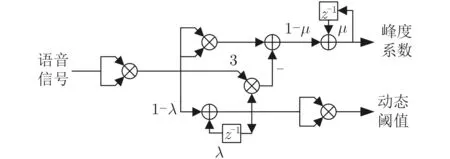
图3 基于FPGA的改进峰度系数迭代方法结构图

6.1 改进的峰度系数计算和动态阈值判决方法

从MATLAB的仿真结果来看，归一化峰度的迭代计算能够有效且直观地检测到脉冲噪声，而且可以以固定的阈值进行判决。然而，归一化峰度计算中包含了FPGA所不擅长的除法运算，为了节省硬件资源，通过结合峰度系数和归一化峰度系数的检测方法，提出改进的动态阈值判决方法。通过2阶累积量对判决阈值进行实时更新，同时计算信号的峰度系数，通过动态阈值进行判决，对脉冲噪声进行实时检测。

6.2 峰度系数计算量评估

经过第4节的推导，对初始迭代式(17)和改进的迭代式(18)的计算量进行估算，如表1。可以看出，改进的峰度系数方法减少了25%的加减法运算和乘法运算，降低了硬件电路的实现成本。

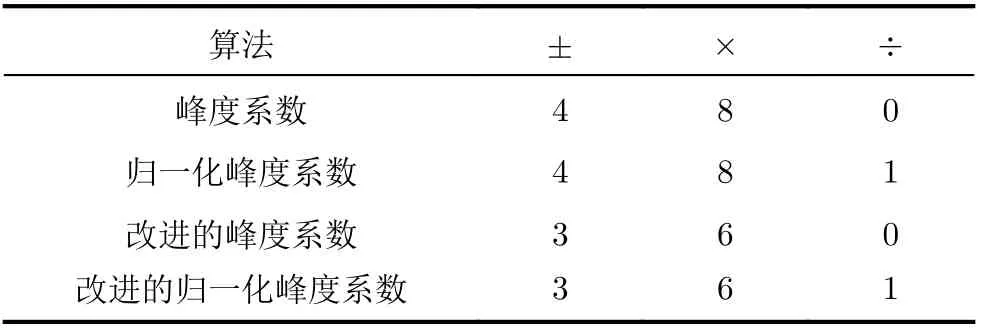
表1 4种峰度系数迭代算法计算量对比

6.3 FPGA仿真结果

由第5节的分析结果，如果使用归一化的峰度系数对脉冲噪声进行检测，在阈值为0时，可以对脉冲噪声和正常语音信号进行区分，根据式(21)，将阈值设置为–0.1，完成动态阈值的计算。FPGA仿真结果如图4所示，波形从上至下分别是语音信号、峰度系数和动态阈值。仿真结果可以看出，脉冲噪声的峰度系数幅度明显高于正常的语音信号，动态阈值则设定了一个范围，将脉冲噪声与语音信号区分开来。

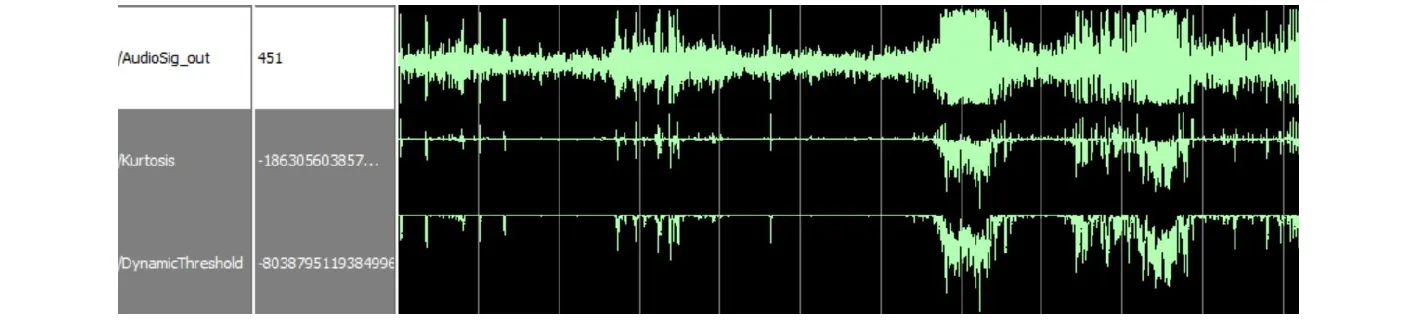
图4 FPGA仿真结果

截取部分仿真数据，在MATLAB中进行分析，图5中，当语音信号产生突发的脉冲尖峰时，峰度系数会大于动态阈值，通过判决，可以认为该部分数据为脉冲噪声。通过置0或者其他抑制方法，可以对脉冲噪声进行抑制。

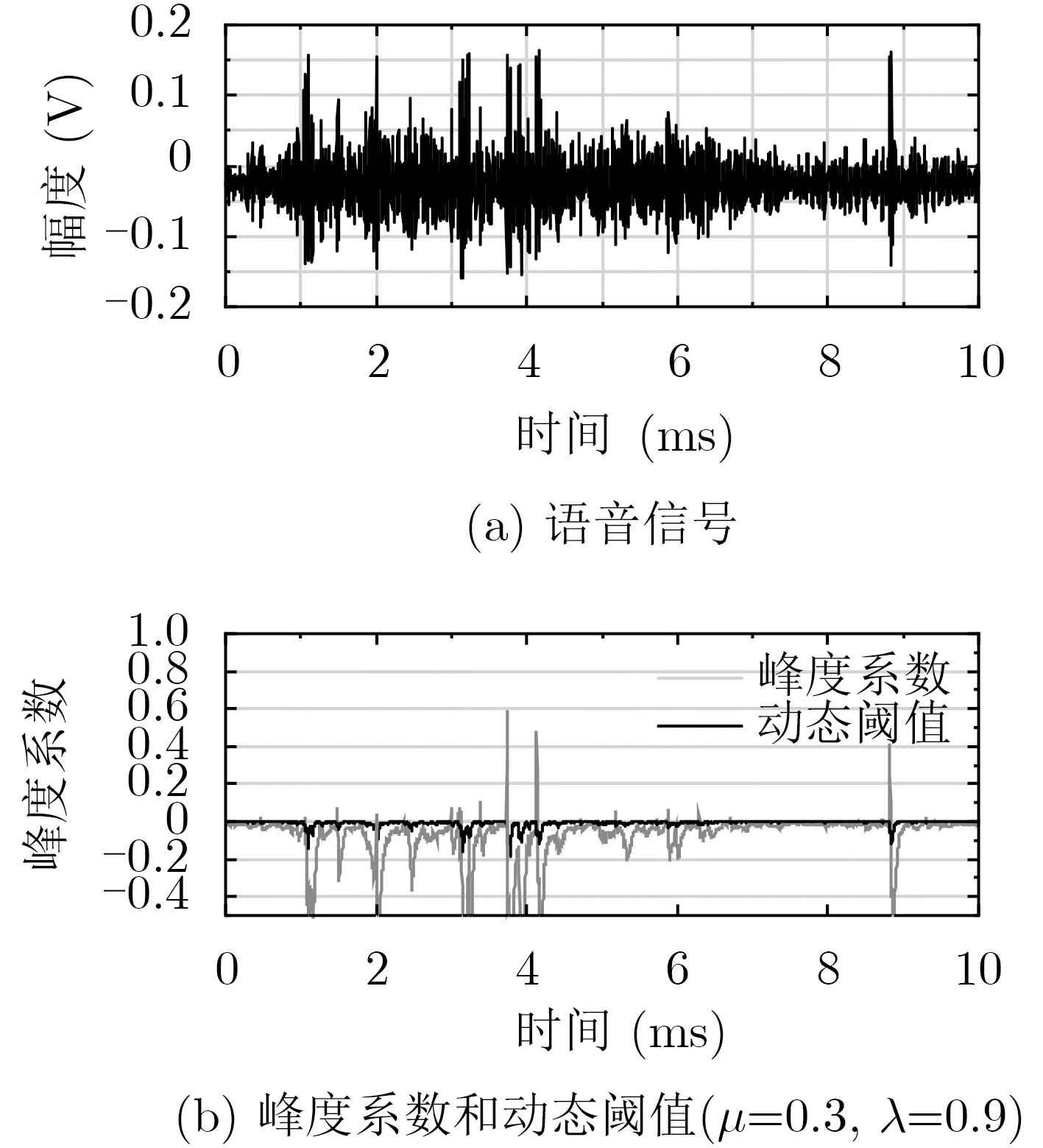
图5 峰度系数与动态阈值分析

7 结论

本文研究了基于高阶累积量的峰度检测算法，从理论层面探讨了该算法在语音脉冲噪声检测中的可行性，根据理论的峰度系数计算公式，推导了峰度系数和归一化峰度系数的数学迭代公式，并进行优化，在降低了25%的计算复杂度的同时，对于较小幅度的脉冲噪声具有更加敏感的检测性能。在FPGA的实现中，提出了动态阈值的判决方法，避免了FPGA所不擅长的除法运算，节省了硬件资源。本文的研究对激光测振系统，语音脉冲噪声检测等方面具有一定的参考价值。