基于装配力的燃料电池性能数值解析
曹爱红,王来华,代世勋
(山东劳动职业技术学院,山东济南 250022)
在燃料电池各组件的装配过程中,装配力对其性能有着十分显著的影响。合理的装配力不仅能够提高燃料电池的气密性,同时能够保证GDL 与BP 之间具有良好的接触电阻。与此同时,能够让GDL 的孔隙率在一个合理的范围内以提高其传质效率。反之,不合理的装配力会对PEMFC 的性能产生负面影响,如果装配力过小,会导致电池的密封性下降,接触电阻过大,进而增大欧姆极化降低电池性能;而如果装配力过大,则将导致GDL 的孔隙率急剧下降,同时会使GDL 的变形增加,进而侵入流道,导致进气量减少以及水气传输受阻[1]。因此,合理的装配力是目前学术界研究的重点。
近年来,有不少学者就装配力与电池性能展开了相关的研究。国内方面,严荣荣等[2]通过热力耦合仿真,探究热力耦合相应对于三个单电池组成的PEMFC 电堆内部的应力分布影响;项忠晓等[3]利用ANSYS 软件,研究了300~600 N 装配力下电池部件变形及应力分布情况,得到了最佳装配压力为400 N(根据作者文中提供的电池尺寸,装配力400 N=2.32 MPa);周怡博等[4]通过建立三维多流道PEMFC 模型,对装配力与气体扩散层厚度及变形的关系展开了研究,以探究装配力对孔隙率、渗透率等参数的影响;吉辰等[5]利用ANSYS 建立PEMFC 单通道三维模型研究了不同装配力下GDL 变形量和孔隙率的变化情况,得到了装配力的合理范围(1.5~2.0 MPa)。国外方面,Taymaz 等[6]研究了装配压力对PEMFC 性能的影响,发现当装配压力合适时,接触电阻和孔隙率会提高,而过大的装配压力会破坏GDL;与Taymaz 不同的是,在考虑热接触电阻和质子传导性时,Atyabi 等[7]得到了最佳装配压力为4.5 MPa。
综上所述,虽然国内外众学者就装配力与PEMFC 性能的关系展开了研究,但是还需要在以下几方面进行进一步的改进:
首先,国内各专家研究了装配力对零部件变形、GDL 孔隙率以及各部件的应力的影响,而没有考虑GDL 变形对流道侵入率的影响以及孔隙率变化对PEMFC 传质的影响。
其次,国外专家的研究对象多为单通道PEMFC,因此在模型方面有待进一步的完善,另外对于GDL 变形与装配力的关系,国外很多专家并没有考虑GDL 材料的杨氏模量与装配力之间的关系。
基于此,文章试图建立三维、稳态、等温8 通道蛇形流道PEMFC 单体模型,结合固体力学、传质、电化学等模型,研究装配力对PEMFC 性能的影响,探究装配力对GDL 厚度、GDL变形量对流道的侵入量、GDL 孔隙率、GDL 与BP 间的接触电阻的影响,进而探究各个因素对PEMFC 水气传输的影响。
1 模型与参数
文章在3.2 cm×3.2 cm 的流场面积内,建立三维、稳态、等温8 通道蛇形流道PEMFC 单体模型、物理模型及数学模型如下文。
1.1 物理模型
图1 为8 通道蛇形流道PEMFC 的物理模型,表1 为模型的基本参数。

图1 8通道蛇形流道PEMFC

表1 模型的基本参数
1.2 数学模型
守恒方程的通用公式如公式(1)所示:

式中的四项由左至右分别为瞬态项、对流项、扩散项和源项。
当ψ分别等于1、Yi(组分:H2O、H2、O2)、T(温度)、(组分:质子电势)或者(组分:电子电势)时,通式就转变成为质量守恒方程(2)、动量守恒方程(3)、物料守恒方程(4)、能量守恒方程(5)以及电荷守恒方程(6)。



其中,ja和jc分别由公式(9)和(10)得出:

除此之外,文章中水的输运问题由公式(11)、(12)求得:
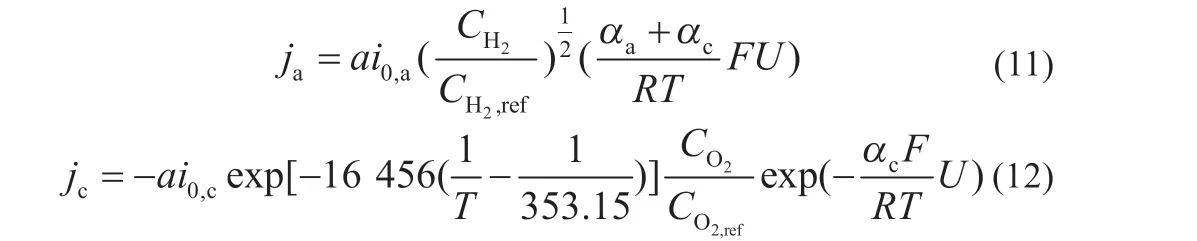
公式中每个符号的含义如表2 所示,每个守恒方程所对应的源项Sψ如表3 所示,PEMFC 的材料性能如表4 所示。
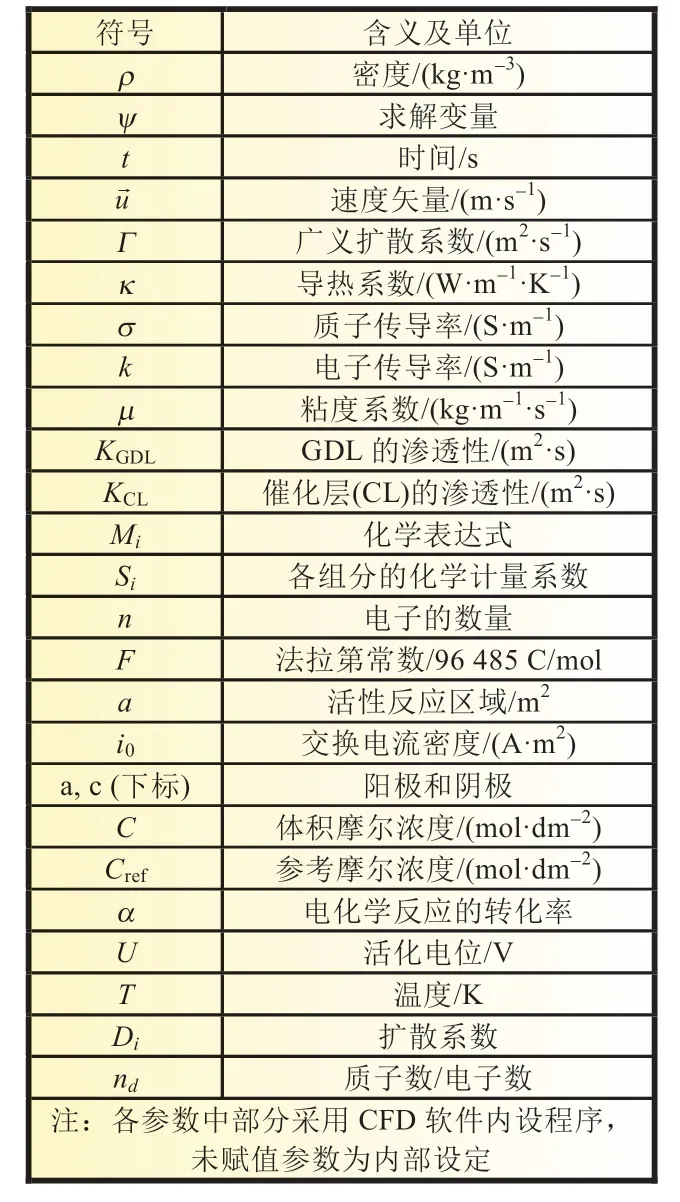
表2 符号及含义
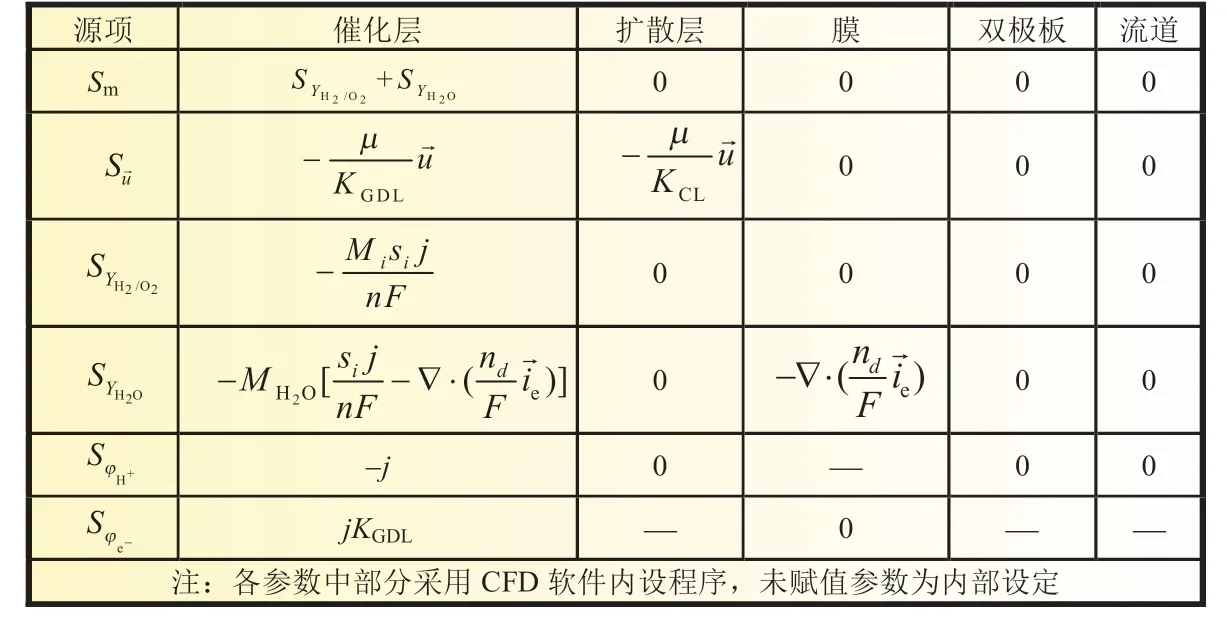
表3 各源项的表达式
表4 中,GDL 的杨氏模量未直接给出,原因在于装配力与GDL 的杨氏模量有着密切的关系,杨氏模量根据公式(13)[8]求得:
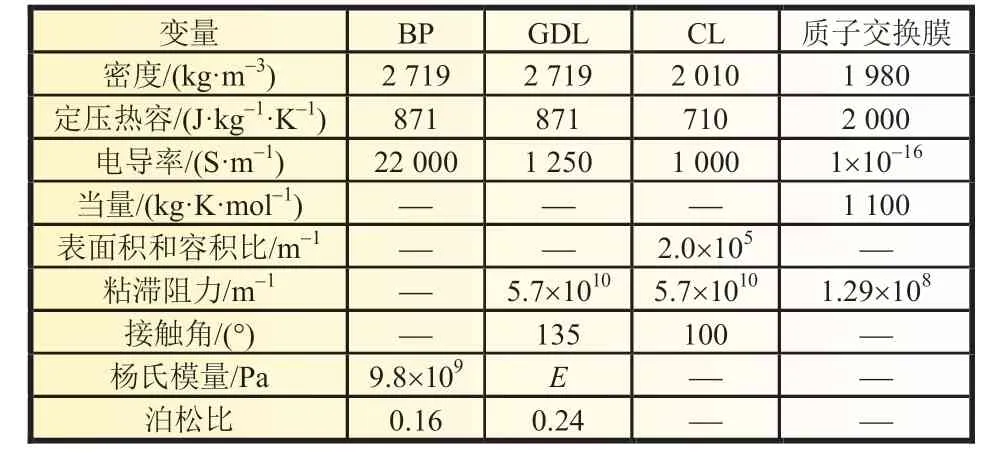
表4 材料的物性参数[8]

式中:ε为正应变;σ为装配力,MPa;E为杨氏模量,MPa。
2 模型假设及模型验证
2.1 模型假设
为了便于计算,本文对PEMFC 计算模型进行了如下假设:
(1)假设PEMFC 处于稳态运行状态;
(2)流道内的气体流动是理想气体的层流和不可压缩流动;
(3)所有气体不能通过质子交换膜(即无气体渗透作用);
(4)忽略重力效应;
(5)GDL 和CL 均为各向同性;
(6)将PEMFC 模型应用于蛇形流道;
(7)流道中的少量液态水是分散的水滴;
(8)除GDL 外,MEA 的其余部件均为不可变形的刚体结构。
2.2 模型验证
图2 为相同条件、相同几何参数(具体参数取值如表5)下数值模拟与实验拟合出的极化曲线对比图,实验装置图如图3 所示。从图3 中可以看出模拟与实验所得出的极化曲线具有较高的一致性,因此可以看出本文所使用的数值模型的可靠性。
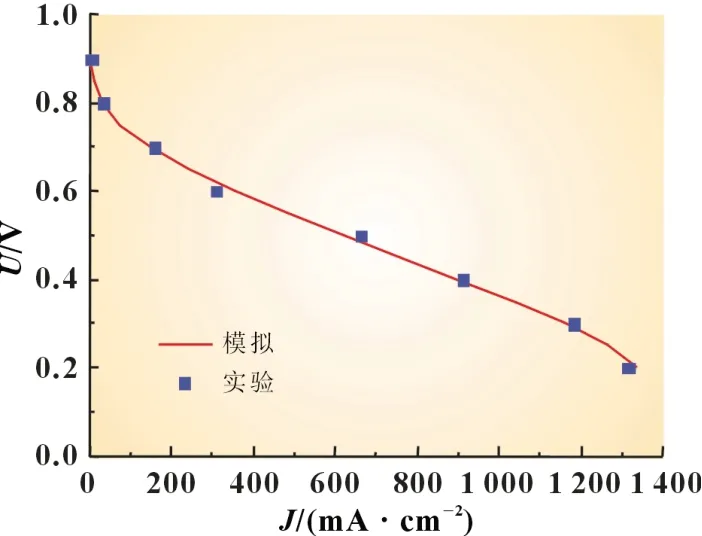
图2 极化曲线对比图

图3 实验装置图

表5 实验PEMFC 条件参数
3 模拟结果分析
3.1 装配力对孔隙率及接触电阻影响分析
根据公式(14)求得GDL 杨氏模量随装配力变化的曲线,如图4 所示。
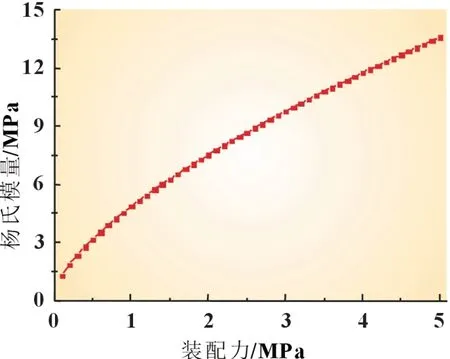
图4 GDL杨氏模量随装配力变化的曲线
文章中装配力与GDL 孔隙率及GDL/BP 接触电阻的关系分别由公式(14)和(15)求出,其中[9]:

式中:εi为初始孔隙率(文章设定初始孔隙率为0.4);εγ为待求解孔隙率;Vγ为装配后的总体积;Vi为初始总体积;VS为GDL的固体体积。
接触电阻的计算公式为[10]:

式中:passembly为装配力;Aassembly为施加装配压力物体表面的面积;pcontact为接触压力;Acontact为接触面积。
图5 为阴极GDL 在施加装配力(2.0 MPa)前后的对比图(基于氢气的扩散性优于空气,且阴极反应有水产生,因此文章仅研究阴极)。从图中可以明显看出施加装配力前后GDL的厚度的变化以及GDL 变形对流道的侵入现象。

图5 GDL变形示意图
图6 为0.1~5.0 MPa 装配力下的GDL 厚度及对流道入侵量的变化曲线,结合公式(13)(14)(15)得到图7 所示的孔隙率随装配力的变化曲线以及图8 所示的接触电阻随装配力的变化曲线。从图8 中可以明显看出,当装配力<1 MPa 时,接触电阻相对较大,且随着装配力的增加变化十分明显,当装配力>1 MPa 后,接触电阻趋于稳定。因此,为了尽可能地控制变量,排除接触电阻对电池性能的影响,文章接下来将在1.0~5.0 MPa 装配力范围内展开进一步的研究。

图6 装配力与GDL变形及流道侵入量关系曲线
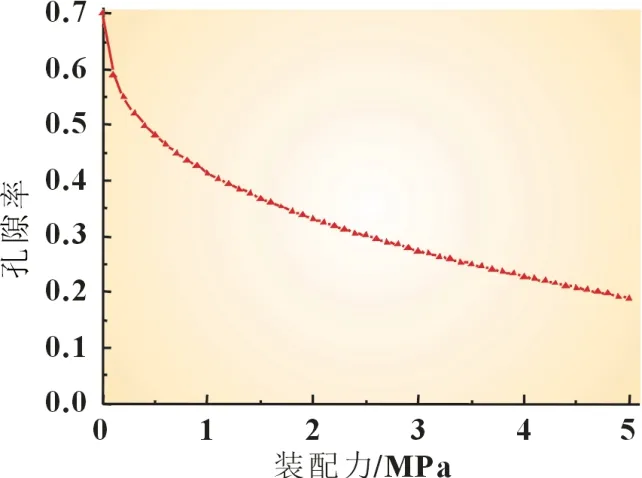
图7 装配力与孔隙率关系图
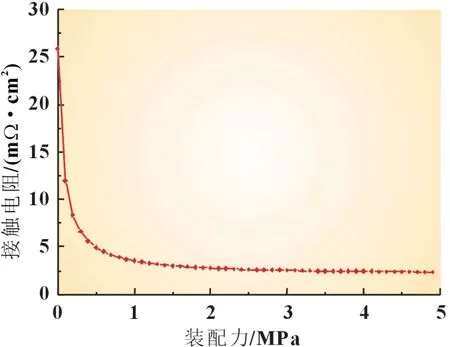
图8 装配力与接触电阻关系图
3.2 基于装配力的PEMFC 性能分析
本部分分别研究了1、2、3、4、5 MPa 装配力对PEMFC 传质的影响(作为对比,文章增加了装配力为0 的情况)。图9 为6 种装配力下PEMFC 阴极GDL 与BP 交界面处最大含水量分布情况。从图中可以明显看出,装配力为1.0 MPa 时的最大水含量与装配力为0 时的水含量几乎相同,说明此时装配力对水含量影响不大,原因在于1.0 MPa 的装配力对于孔隙率的影响不大,进而对GDL 内部水传输影响不大。此外,随着装配力的增加,最大水含量逐渐增大,说明较大的装配力容易使水传输受阻;与水分的传输相同,装配力对于GDL 气体分布影响呈相同的规律,如图10 所示。当装配力为1.0 MPa时,氧气浓度分布的均匀性最好,且随着装配力的进一步增大,氧气浓度分布均匀性逐渐降低,这说明装配力为1.0 MPa时的GDL 内气体传质效果最佳。

图9 装配力与最大含水量的关系
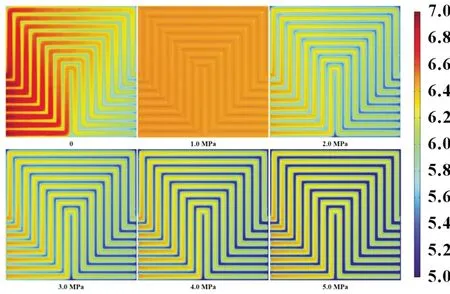
图10 装配力与GDL氧气浓度分布
通过对比6 种装配力模型的电化学性能(如图11 所示),可以看出装配力1.0 MPa 下的电化学特性均优于其余5 种模型,无论是在浓差极化区域,还是在欧姆极化区域,这与1.0 MPa 装配力下的接触电阻、孔隙率的最优分配有直接关系(过小的装配力能够获得较大的孔隙率进而提高传质,但接触电阻过大降低欧姆极化性能;而过大的装配力能够获得较小的接触电阻,但孔隙率较低,不利于传质),因此,文章的最优装配力为1.0 MPa。
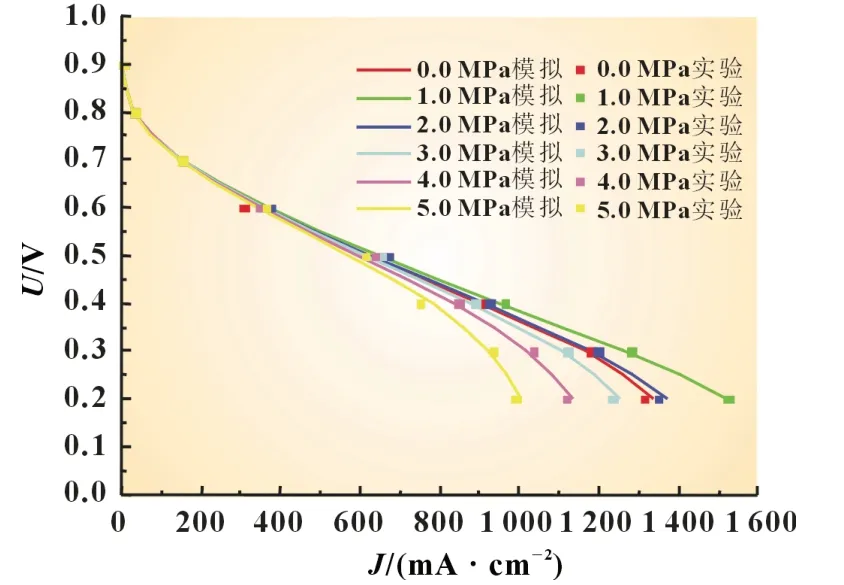
图11 电化学性能对比
4 结论
文章基于装配力与GDL 孔隙率、GDL 厚度、GDL 变形对流道的侵入量、接触电阻之间的关系对装配力与PEMFC 性能之间的关系展开了研究与讨论,结论如下:
(1)基于GDL 材料的多孔性与特殊性,装配力对其变形的影响受到GDL 杨氏模量的限制,随着装配力的增加,GDL 的杨氏模量不断增大,最终导致GDL 的厚度及GDL 变形对流道的侵入量的增/减幅逐渐减少;
(2)随着装配力的增加,GDL 的孔隙率逐渐降低,减幅也逐渐降低;在0.1~1.0 MPa 之间,接触电阻随着装配力的增加而急速下降,在1.0~5.0 MPa 之间,接触电阻基本保持不变;
(3)装配力会对PEMFC 的传质、电化学性能产生影响,当装配力>1.0 MPa 时,随着装配力增加,PEMFC 传质、电化学性能逐渐下降,综合考虑接触电阻、传质等因素,最佳装配力为1.0 MPa。

