电力系统稳定器在西藏JC水电站应用

陈秋林，刘 甫，马大海，刘德翼，龙远扬

（1.华能西藏雅鲁藏布江水电开发投资有限公司，西藏 山南 856400；2.西藏电力调控中心，西藏 拉萨 850000）

“十三五”以来，西藏自治区的经济获得了突飞猛进的发展，2020年地区GDP达到1 800亿元，电力装机容量接近400万kW。川藏电力联网工程建成投运，成功地解决藏中电网频率稳定的问题；阿里与藏中电网联网工程建成投运，实现了将藏中电网电能输送到阿里电网，解决了阿里地区38万多人的用电难题。目前，西藏主电网已覆盖全区74个县（区）。

西藏地域面积122.84万km2，2018年末常住人口343.82万人，人员居住比较分散。川藏联网工程全长1 500多km，阿里电力联网工程全线长1 600多 km。西藏电力能源主要以光伏发电和水力发电为主，供电面积广、负荷分散、长距离输电、能源结构不稳定等因数，造成西藏电网电能质量很难得到保证，特别是长距离输电，在大负荷切换时，很容易造成电网低频振荡。

JC水电站是“十二五”期间开工建设，“十三五”收官之年投产的西藏唯一大型电源电站，也是目前单机容量最大的电站，电站安装3×120 MW水轮发电机组，总装机容量360 MW。电站两回220 kV出线接至朗县500 kV枢纽变电站。JC电站机组的稳定性关系到藏中电网的电压、频率稳定。电站调速器控制系统加装一次调频设备能够有效地解决系统的功率稳定；励磁控制系统加装电力系统稳定器（PSS），能够提高输送功率的极限，并且能有效抑制机组和系统产生的有功功率低频振荡。

1 低频振荡产生的原因

全国联网工程的研究表明，随着电网规模扩大和输送功率增加，系统动态稳定问题（低频振荡问题）已成为影响互联系统安全、稳定、经济运行的最重要的因素之一。互联电力系统中一般都存在两种振荡模式，即地区性振荡模式（频率一般在0.5～2.0 Hz）和区域间振荡模式（频率一般在0.1～2.0 Hz）。

为解决这些问题，重要的发电机励磁控制系统需要投入电力系统稳定器（PSS），PSS除了能抑制本机组的低频振荡外，还能有效地抑制区域间低频振荡，保证联网系统的安全、稳定、经济运行。

导致电力系统低频振荡的原因是多方面的，它与电力系统结构和发电机工况有关，也与励磁控制系统有关。电力系统低频振荡与励磁控制系统有关是指当发电机转子角度（△δ）的变化引起电气量的变化，经过励磁调节的作用会对发电机转子运动产生影响，当采用快速励磁系统时，该影响就是提高了同步力矩，削弱了阻尼力矩，加重了发电机转子的振荡。这就是通常所说的用快速励磁系统更易导致低频振荡的原因。

发电机功角δ（也称转子角度）是发电机内电势与电压之间的相位差，表明系统的电磁关系之外，还表明了发电机转子之间的相对空间位置。发电机正常运行时输出的电磁功率Pe=P0，此时，发电机转子上作用着两个转矩：一个是原动机的转矩Mm（或用功率Pm表示），它推动转子旋转；另一个是与发电机输出的电磁功率Pe相对应的电磁转矩Me。在正常运行的情况下，两者相互平衡，即Pm=Pe=P0。发电机以恒定速度旋转，且与系统的转速（指电角速度）相同（设定为同步速度ωn）。

根据旋转物体的力学定律，同步电机的转子运行方程如式（1）所示：

式中，M—发电机转子转动惯量；Mm—原动机转矩；Me—发电机电磁转矩；ω—转子旋转角速度；δ—发电机功角。在速度变化不大时，可用功率代替转矩，则有

根据发电机功率特性可知，对于隐极式发电机纵轴电抗Xd与横轴电抗Xq相等,故隐极式发电机功率特性为：

式中，Eq—发电机内电势；U—发电机出口电压；XdΣ—发电机及出口回路电抗之和；δ—发电机功角。

对于凸极式发电机来说Xd≠Xq，相比隐极式发电机来说，多了一项与发电机电势Eq（励磁电流产生的）无关的两倍功角的正弦项，是由于发电机纵轴、横轴磁阻不同而引起的，又称为磁阻功率。凸极式发电机功率特性为：

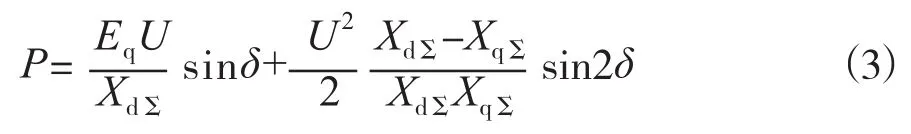
为了分析发电机各状态量之间关系，依据单机—无穷大系统，忽略发电机定子电阻、定子电流的直流分量，以及阻尼绕组的作用，推导出发电机的基本方程，并得出同步发电机研究用数学模型，即海佛容-飞利蒲斯（Heffron-Philips）模型，如图1所示。

图1 应用于小干扰分析的同步发电机数学模型

图1中△Mm为转子的机械转矩，△Me为转子输出的电磁转矩Me=△Me1+△Me2。系数K1至K6的定义如下：

K1—d轴磁通为常数时，由于转子角度δ的变化，引起的电磁转矩△Me的变化量；

K2—转子角度δ为常数时，由于d轴磁通的变化，引起的电磁转矩△Me的变化量；

K3—阻抗因数；

K4—转子角度δ变化引起的去磁效应；

K5—d轴磁链的电压为常数时，由于转子角度δ的变化，引起的发电机端子电压U的变化量；

K6—转子角度δ为常数时，由于d轴磁链的变化，引起的发电机端子电压U的变化量。

除K3以外，系数K1到K6均受发电机的运行点的影响。所有的系数一般都为正，系统是稳定的。然而在负荷较重的情况下，K5可能为负，就会造成系统不稳定状况。

图1中虚线框内，体现了同步发电机转子运动方程回路，即为发电机的机械环节，决定了机组自身的振荡频率，虚线框下半部分则是发电机的电磁环节。

对于发电机振荡过程的研究证明，在多数情况下，决定发电机转子振荡的量△δ和△ω是与机械惯性时间常数决定的，振荡频率低且衰减缓慢；而与励磁系统有关的变量△Efd和△E'q是由相对较小的时间常数决定的，振荡频率高且衰减较快。

研究表明，因磁链变化（包括励磁调节控制的作用）产生的转矩可分为两个分量，即与△δ成比例的同步转矩△Ms△δ和与转速△ω（或s△δ）成比例的阻尼转矩△MDs△δ，即：

式中，△Ms—同步转矩系数；△MD—阻尼转矩系数。同步转矩是由定子电流去磁效应产生的，所以是负值，阻尼转矩是由励磁绕组本身产生的，是正值。

当发电机Pm＞Pe时，转子角度δ增大，机端电压U下降，经过励磁控制器的调节作用，励磁电压升高，励磁电流增大，但发电机磁链的增长由于励磁绕组的惯性作用要滞后一段时间，以至于转子向回摆动（△δ减少），转速增加值△ω成为负值时，磁链仍在增大，制动的电磁转矩也在增大，以至使转子向回摆的幅度增大，起了相反的作用，这就是所谓的励磁控制产生“负阻尼”的根本原因。

对于以机端电压作为反馈对象的自动励磁调节器来说，本质上是不利于系统阻尼的，放大倍数越大且反应越灵敏，越是容易产生负阻尼。但是对于发电机的暂态稳定性来说，又需要提高自动励磁调节器的放大系数和响应时间才能满足要求。

2 电力系统稳定器（PSS）原理简介

由上面的分析可知，采用机端电压作为反馈控制量的励磁调节器恶化了系统阻尼。在长距离输电、负荷较重时，若转子角度δ出现振荡，励磁调节器提供的附加磁链的相位是落后于δ角度的振荡，它的一个分量与转速相位相反（即产生了负阻尼转矩），使角度δ振荡加大，系统失去稳定。

如果在励磁控制系统中采用附加控制系统，使励磁调节器产生的附加磁链在相位上领先转子振荡角某个角度，从而产生正阻尼转矩，使振荡逐渐衰减。这个附加控制就是PSS，如图1右下角所示。它的作用见图2所示。

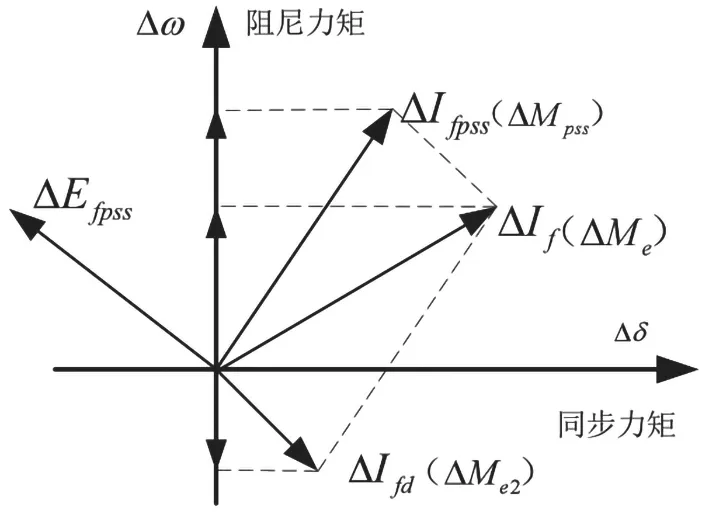
图2 PSS作用原理图（阻尼转矩相量图）

图2中，△ω—发电机转速偏差（阻尼转矩）；△δ—功率角偏差（同步转矩）；Efpss—PSS输出的电势量；Ifpss—PSS输出的电流量；Ifd—调节器输出的励磁电流和由于功率角δ摆动在转子上感应的滑差电流之和；If—Ifpss和Ifd叠加后的电流。

图2中，如果不叠加PSS电流量，励磁电流Ifd产生的转矩在△ω轴上投影在负半轴上，阻尼转矩为负。PSS的作用就是在励磁调节器中引入一个矢量控制信号，这个信号可以是有功功率P的变化量△P（等同于△δ），也可以是频率的变化量△f（等同于△ω）。将这个矢量信号超前一定角度，幅值根据实际情况予以放大，这个矢量即是△Efpss所产生的电流△Ifpss与励磁电流Ifd的矢量和△If，它所产生的电磁转矩△Me在△ω轴上的投影为正。即是PSS的输出产生的电磁环节为机组提供了正阻尼转矩，有利于机组及系统的安全稳定运行，这就是PSS的作用原理。

3 JC电站励磁系统参数及PSS控制模型

JC水电站发电机是浙江富春江水电设备股份有限公司生产的120 MW发电机组，采用单元接线方式。励磁方式采用静止可控硅自并励励磁系统，励磁调节器为广州擎天实业有限公司生产的EXC9200型数字式励磁调节器。采用双通道励磁调节器，控制方式为并联型PID+PSS控制，采用余弦移相原理,PSS采用PSS-2B控制模型。

发电机参数见表1所示。

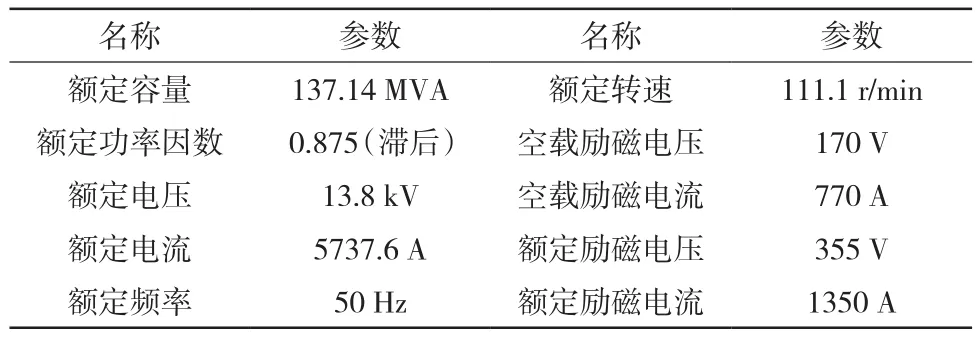
表1 发电机参数

励磁调节器自动调节PID控制模型，采用两级超前／滞后校正环节，数学模型见图3所示。

图3 EXC9200型数字式励磁调节器PID数学模型

图3中控制参数说明见表2所示。

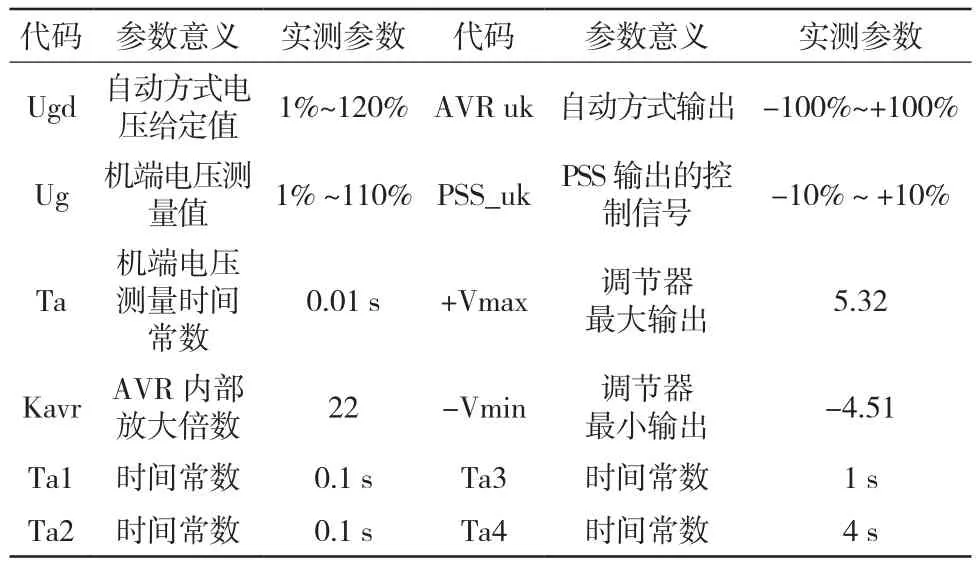
表2 PID数学模型控制参数

EXC9200型励磁调节器PSS采用GB/T 7409 标准规定的PSS-2B型数学控制模型。PSS调节通道有测量单元、隔直单元、比例放大单元、三级超前-滞后校正单元、限幅单元组成。输入信号采用加速功率作反馈信号（即双变量ΔP、Δω）。数学模型见图4所示。

图4 EXC9200型数字式励磁调节器PSS-2B数学模型

图4中控制参数说明见表3所示。

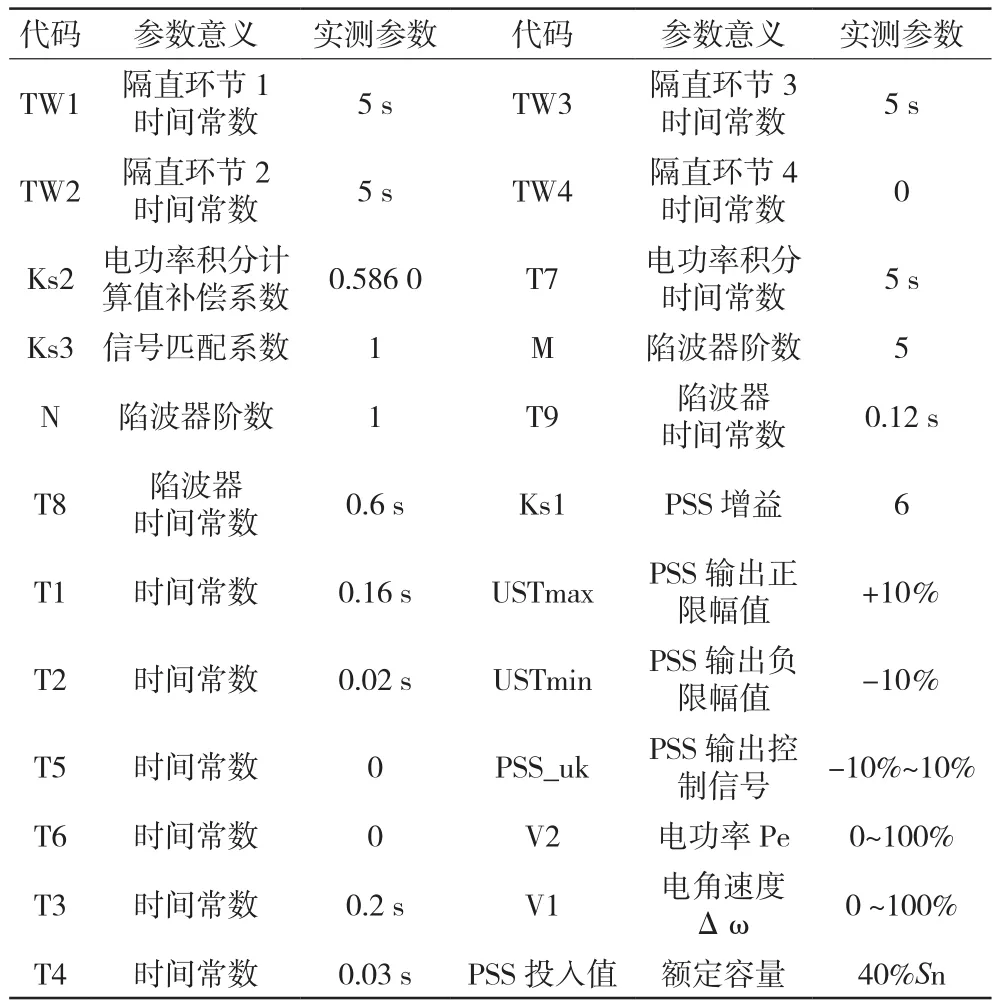
表3 PSS-2B数学模型控制参数

4 PSS试验

PSS试验前，完成励磁调节器建模试验，将PID等参数整定完毕（参数见表2所示），并完成所有的励磁系统静态、动态试验，验证励磁调节器参数合理并满足要求。下面以1号发电机PSS试验过程为例介绍PSS试验过程。

4.1 励磁系统无补偿相频特性测量

P=80 MW，Q=1.5 Mvar，退出机组PS S、AGC功能。在PSS输入端加入白噪声信号（伪随机信号），用频谱仪测量白噪声信号和发电机电压信号之间的相频特性，测试结果如表4所示。

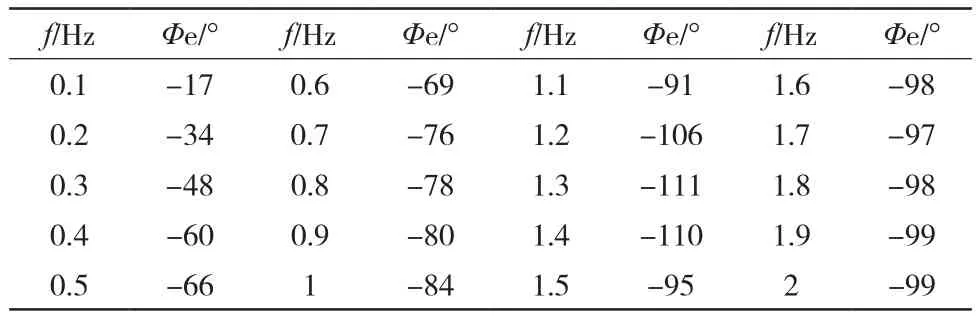
表4 励磁系统无补偿相频特性

4.2 励磁系统有补偿相频特性仿真

PSS参数整定的目的是使PSS在本机发生振荡和联网后系统发生振荡时均能有效地抑制，所以，在励磁系统加入PSS后产生的合成电磁转矩△Me在0.1～0.3 Hz（不含0.3 Hz）频率段应超前△ω轴不大于 30°，在 0.3～2.0 Hz频率段超前△ω轴 20°和滞后△ω轴45°之间。即在0.3～2.0 Hz范围内滞后 - △Pe（加速力矩）70°～135°之间。用Φe表示励磁系统滞后相位，用Φpss表示PSS超前相位，则应该使Φc=（Φe+Φpss）在70°～135°范围内。

将表4数据采用专用软件仿真，仿真出PSS参数，然后计算出1号机组投入PSS功能后的相频特性和有补偿特性，数据见表5所示。

表5 励磁系统有补偿相频特性

由表5可以看出，在0.1～2.0 Hz频率范围内，有补偿特性在-60.6°～-110.1°之间，由PSS产生的电磁力矩的阻尼力矩（在△ω轴上的投影）分量为正，PSS相位补偿满足要求。

根据表5数据，可以画出1号机励磁系统的频率特性，如图5所示。

图5 1号机组励磁系统无补偿、有补偿、PSS频率特性曲线

4.3 PSS增益临界试验

理论上在相位补偿正确的情况下，PSS的增益越大，其作用效果越明显（提供的阻尼力矩越大），但是由于电力系统是一个复杂的高阶系统，PSS的增益如果调整得过大，容易引起PSS控制环节振荡，反而使系统出现不稳定现象，因此PSS实际存在着一个最大增益，即临界增益。

试验方法：投入PSS功能，逐步增大PSS放大系数Ks1，观察发电机的实时录波图，直到发电机电压、励磁电压出现1～4 Hz的剧烈振荡，这时的PSS增益即为临界增益。PSS运行的增益一般取临界增益的1/3～1/5，1号机组PSS增益Ks1取6。

4.4 PSS阻尼效果试验

采用阶跃试验方法分别对比PSS投入、退出时阶跃响应曲线。未投入PSS时曲线见图6，投入PSS功能时曲线见图7。试验工况P=80 MW，Q=1.5 Mvar，阶跃量2%，Ks1=6。

图6 未投入PSS时阶跃响应图

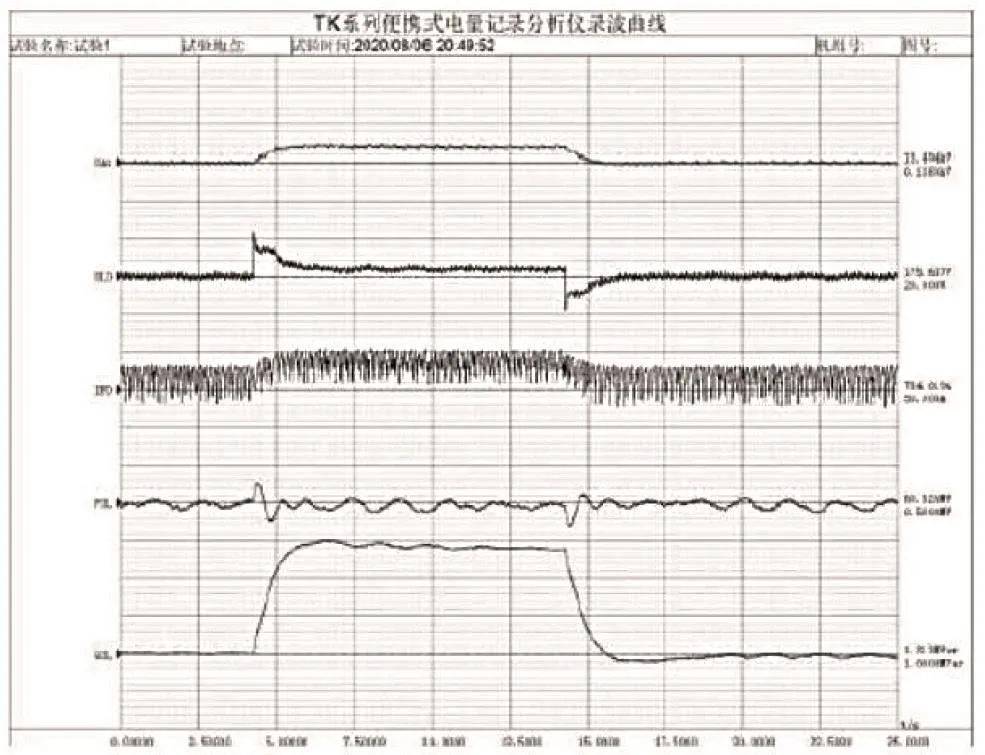
图7 投入PSS时阶跃响应图

试验结果表明，投入PSS功能后，有功功率振荡在第二个振荡周期开始就被抑制，控制效果非常明显。

4.5 PSS反调试验

PSS的作用是在系统出现有功功率低频振荡时，通过励磁系统的作用抑制振荡，可以理解为是通过无功功率的波动来抑制有功功率的波动。由于水轮发电机组增减负荷的速率很快，如果PSS参数整定不当，在增减负荷过程中，会发生较大的无功功率波动，就是所谓的反调现象。PSS-2B型电力系统稳定器采用电功率信号ΔP和转速信号Δω作为反馈输入信号，能有效抑制反调发生。

试验方法：投入PSS功能，P=80 MW，以最快速度增加20 MW、减少20 MW的功率调节，观察PSS是否有反调现象见下图所示。快速增减20 MW负荷时，无功最大变化量为2 Mvar，未出现反调现象。

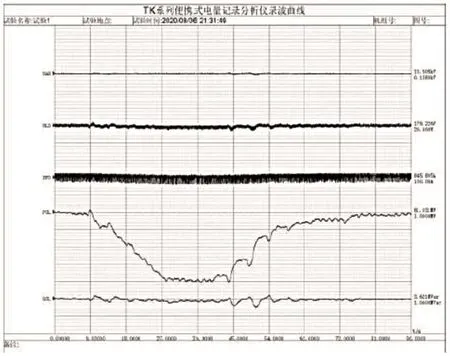
图8 反调试验波形

5 小结

JC水电站3台机组分别于2020年8月、10月、12月投产。机组投产前均通过了中国电科院、西藏电科院联合测试，完成了励磁系统建模、PSS试验等。经过频率响应特性试验、仿真计算、临界增益试验、阶跃干扰试验和反调试验等，证明PSS在有功功率发生0.1～2.0 Hz的低频振荡有非常明显的抑制作用。

试验证明，JC水电站励磁控制系统投入PSS功能后能有效地抑制本机低频振荡，增加了机组及系统的正阻尼，提高了系统输送功率极限，增强了系统稳定性。