受端电网STATCOM布点及容量规划的凸松弛方法
马骞,邓卓明,吴云亮,李鹏,姚文峰,郭知非
(1.中国南方电网电力调度控制中心,广州510663;2. 南方电网科学研究院,广州510663)
0 引言
受端电网的电能往往由其外部远距离的发电厂通过高压输电线传输获取,并且对应着密集的工商业负荷,换流站、输电线路以及异步电动机、电弧炉、降温压缩电机等负荷的无功功率需求量巨大[1]。在负荷侧安装一定数量和容量的静止同步补偿器(static synchronous compensator, STATCOM)做无功补偿,不仅能在电网稳定运行时维持电压稳定、提高供电质量、降低电能损耗,同时在发生较为严重的短路故障时,能提供坚强的无功支撑,快速恢复电压至安全水平,避免甩负荷。目前在经济条件相对较好的广东电网,已经逐渐在负荷端如东莞、水乡配置了STATCOM[2]。STATCOM的规划和控制也获得了越来越多的关注。文献[3]提出了在多直流馈入系统各母线对多回直流逆变站电压支撑强度的指标,并用于南方电网STATCOM配置方案的研究。文献[4]描述并复现了HVDC系统在故障恢复过程中发生“二次换相失败”的现象,提出了根据故障的严重程度差异化配置STATCOM无功补偿模式。STATCOM作为一种新兴的电力电子无功补偿装置,尽管有着极其优秀的无功补偿性能(反应时间短,补偿容量灵活多变),但是其造价仍然高昂,规划配置STATCOM必须精打细算,避免电网投资的浪费[5]。
目前电网规划人员对STATCOM的规划配置大多采用枚举试错的方式,通过大量的仿真试验获得满足安全约束的规划方案。然而,大量的仿真试错不仅工作量巨大、耗费大量的时间,而且获得的规划方案也仅仅是一个相对较好、能满足安全约束的方案,并不是最经济的方案。并且现代电力系统模型越来越复杂,规模也越来越大,组合爆炸的问题将导致枚举无法进行。
因此,国内外一些文献提出了数学化的规划方案。在规划STATCOM的配置时,需要考虑STATCOM的安装地点以及安装容量,即对应定点和定容的规划。对此国内外已有相应的研究成果。文献[6 - 7]采用基于动态无功—电压灵敏度的电压控制敏感因子和多馈入相互作用因子,计算获得电压控制敏感点,以便确定动态无功源的布点。在此基础获得候选节点后,文献[8]进一步采用基于分解的多目标进化算法确定动态无功源的容量。文献[9]指定动态无功—电压灵敏度最大的节点为候选节点,然后指定STATCOM的容量为对应节点补偿的上限值。文献[10]利用轨迹灵敏度计算和奇异值分解确定动态无功源的布点,然后通过时域仿真和非线性优化之间的交替迭代获得规划容量。尽管上述的方法能够获得相对较好的、工程上能用的规划方案,然而,因为它们把动态无功源布点及容量完全割裂开来,获得的规划方案只是布点和容量二层的分别最优,并不是它们整体的最优方案。
为此,本文分别采用整数变量和连续变量表征STATCOM的安装地点和安装容量,把整体的规划问题解析为数学上的混合整数规划模型,以便获得布点和容量规划的整体最优方案。为了提高求解效率,本文采取了凸松弛技术[11 - 13],借助STATCOM布点的某些特征,关于整数变量整体凸化原始的混合整数规划模型,然后对凸模型实施一种紧松弛。经算例验算,本文的混合整数规划模型和凸松弛技术能够获得STATCOM定点和容量的最优规划方案,有效缓解电网短期电压失稳的问题。同时,相比割裂布点和容量的传统规划方法,本文的方法获得的规划方案更优,即规划的费用更小。本文的创新在于提出一个通用的混合整数规划模型和凸松弛求解方案,避免大规模枚举和试错仿真工作,并且获得最经济的规划方案。同时,得益于电网元器件的模型的通用性,本文提出的优化模型可以实施封装,后续可以根据用户需要对模型进行修改,从而推广到其他的电网。该模型的通用性将可以节省大量仿真试错的工作量和时间。
1 STATCOM规划的混合整数规划模型
1.1 目标函数
本文目标函数J(·)定义为STATCOM规划方案的投资费用,包括与基建相关的固定安装费用(例如征地补偿)以及与容量相关的容量费用(例如设备购置)2个部分。STATCOM总体的规划投资费用由固定安装费用和容量费用叠加[14]。
J(·)=vT[c1e+c2·(QCmax-QLmax)]
(1)
式中:v为STATCOM安装地点的二进制列向量(即所有元素皆为二进制数值),其中第i个元素的数值为0,代表候选节点i不安装STATCOM,无需记及固定安装费用和容量费用,第i个元素的数值为1,代表候选节点i安装STATCOM,需要记及固定安装费用和容量费用;c1为固定安装费用,万元;c2单位容量费用,万元/Mvar;e为单位列向量;QCmax=[qc1,qc2,qc3,…,qci]为STATCOM的容性输出限值列向量;QLmax=[ql1,ql2,ql3, …,qli]为STATCOM的感性输出限值列向量;其中第i个元素qci和qli分别对应候选节点i的容性容量(正值)和感性容量限值(负值)。需要注意的是,QCmax和QLmax均为可参与优化的变量,而不是固定不变的参数。
在极小化目标函数(即规划投资费用)的过程中,各个站址STATCOM的配置容量(即QCmax-QLmax)会逐渐下降直至收敛,极小化目标函数能够限值各个站址的配置容量。
1.2 电压和功角安全约束
根据南方电网安全稳定导则,电压安全约束为故障清除1 s时间内,节点电压恢复至0.75 p.u.以上。
Vl.k(t)≥0.75,t∈[tc+Td,tf]
(2)
式中:l和k分别为节点编号和故障编号;t为仿真时刻;tc和tf分别为故障清除时刻和仿真终止时刻;Td为持续时间1 s;Vl.k(t)为节点电压。
功角安全约束则必须保证所有发电机功角与惯量中心转子角的功角差小于给定的数值120 °。
|δg.k(t)-δCOI.k(t)|≤δmax
(3)
式中:g为发电机编号;δg.k(t)为发电机功角;δmax为给定的阈值120 °;δCOI.k(t)为惯量中心转子角。
(4)
式中:Mg为发电机惯量;NG为发电机数量。
此外,约束条件还应包括动态设备的微分代数方程、系统的潮流方程、变量上下限约束以及边界约束等等。因为这些方程都比较常规且繁琐,此处不一一列举,具体的方程可参考文献[9,15]。其中,发电机采用经典四阶模型,励磁系统采用经典四阶模型,异步电机负荷采用经典三阶模型,STATCOM采用增益-时间-常数模型。
1.3 STATCOM容量约束
在实际工程中,各个站址由于场地、检修等限制,可能存在数值不相等的受限容量。该限制可以通过控制变量QCmax和QLmax的上下限约束(不等式约束)表达。
(5)
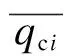
1.4 混合整数规划模型
STATCOM规划问题的混合整数规划模型可采用简约形式表示,具体如式(6a)—(6e)所示。

(6a)
(6b)
0=Gk(xk(t),yk(t),u,v)
(6c)
0≤Hk(xk(t),yk(t),u)
(6d)
v∈{0, 1},t∈[t0,tf]
(6e)
式中:xk(t)、yk(t)、u、v分别为状态变量、代数变量、连续决策变量(即规划安装容量)以及二进制决策变量(即规划安装布点)的列向量;t0为仿真起始时刻;在方程方面,式(6b) 为微分方程,包含发电机及其励磁系统、异步电机负荷以及STATCOM的动态;式(6c)为受端电网的潮流方程,其中STATCOM以注入功率的形式挂在对应节点上;式(6d)包含所有变量(状态变量、代数变量和决策变量)的上下限约束以及1.2节提到的电压和功角安全约束。关于式(6b)提到的设备模型和微分方程可参考文献[9,15]。
2 混合整数规划模型的凸松弛
凸松弛方法是一种针对和处理混合整数规划问题的处理方案。经过凸松弛处理,混合整数规划的求解效率可以极大提高。凸松弛包含2个步骤:凸化以及松弛。
凸化过程需要列举二进制决策变量的所有可能组合,然后混合整数规划模型整体关于二进制决策变量做线性叠加。

线性叠加可以使得规划模型关于二进制变量整体凸化。因为STATCOM以注入功率挂在潮流方程对应节点,该功率存在与否是由决策变量v决定的。因此潮流方程(6c)是直接与v相关的。此外,在1.1节介绍过目标函数也是与v直接相关的。除此以外,微分方程、上下限约束和安全约束都没有与v直接相关。因此只需对式(6a)和(6c)做关于二进制变量的线性叠加即可。
本文借用一个虚拟4节点网络为例子详细介绍凸化。假定在该虚拟的4节点网络中,节点1—3为负荷节点,并被选为STATCOM的候选节点,节点4是平衡节点。因为在此案例共3个候选节点,每个节点安装或不安装(1/0)共2种情况,共有8种布点方案,具体如表1所示。

表1 虚拟案例的8种布点方案Tab.1 Eight plans of locations in the virtual case
为表1中每种组合引入替代变量αw。 依据线性叠加的计算,节点1—3的潮流方程可分别凸化为:
(7a)
(7b)
(7c)
式中Gl.k(xl.k,yl.k,ul,vl.w)和vl.w分别为节点l的潮流方程函数以及vw的具体值。
由表1和式(7a)—(7c)可知,因为整数决策变量共8种组合,凸化需要枚举8次,引入8个替代变量,才能完成线性叠加。然而,α1-α8实际并非独立变量,可以做一定的简化。在对应的潮流方程上分别引入变量θ1.1=α1+α2+α3+α5,θ1.2=α4+α6+α7+α8,θ2.1=α1+α2+α4+α6,θ2.2=α3+α5+α7+α8,θ3.1=α1+α3+α4+α7, 以及θ3.2=α2+α5+α6+α8, 其中θl.i代表节点l的第i个θ变量。式(7a)—(7c)可简化为:
0=G1.k(x1.k,y1.k,u1, 0)θ1.1+G1.k(x1.k,y1.k,u1, 1)θ1.2
(8a)
0=G2.k(x2.k,y2.k,u2, 0)θ2.1+G2.k(x2.k,y2.k,u2, 1)θ2.2
(8b)
0=G3.k(x3.k,y3.k,u3, 0)θ3.1+G3.k(x3.k,y3.k,u3, 1)θ3.2
(8c)
并且同样满足θ1.1+θ1.2=1,θ2.1+θ2.2=1以及θ3.1+θ3.2=1的约束条件,且θl.i为二进制变量。这是因为STATCOM以注入功率挂在负荷节点上,节点l安装STATCOM与否只影响节点l列写潮流方程,并不影响其他节点列写相应的潮流方程,因此节点间列写潮流方程是相互独立的。
同理,对于目标函数J(·), 假定Jl(ul,vl.w)是节点l规划安装STATCOM的费用,则目标函数可凸化如式(9)所示。
(9)

松弛过程则把上述的替代变量θl.i从二进制的取值范围松弛至连续区间[0,1],混合整数规划模型整体转换为连续规划问题,从而避免了直接求解混合整数规划问题。在优化领域,基于梯度的算法或求解器都能比较高效地求解连续规划问题,因此提高了STATCOM规划的效率。同时,经文献[11 - 13]的验证,上述关于整数变量的凸化及松弛是一个紧松弛过程,可以获得满足边界条件约束的规划方案。
3 整体规划流程
依据上述的混合整数规划模型以及凸松弛方法,本文归纳了STATCOM的整体规划流程如下。
1)采用三相接地短路故障N-2扫描受端电网薄弱区域,获得电网在规划STATCOM前的短期电压失稳的故障集;
2)以安装费用最小为目标函数,建立全网电压安全约束的STATCOM布点及容量规划的规划模型式(6a)—(6e);
3)枚举二进制布点变量v的所有组合,采用固定的列向量vw(w= 1, 2,…,NW)代表对应的每1种规划方案;

5)关于二进制变量,整体做线性叠加以凸化混合整数规划模型;
6)松弛替代变量θl.i至连续区间[0,1];
7)在通用代数建模系统(general algebraic modeling system,GAMS)上调用CONOPT求解器[16]求解经过凸松弛处理后的连续优化模型,获得STATCOM布点及容量规划方案;
8)采用PSD-BPA软件仿真校验规划方案是否满足暂态电压、功角稳定约束。
4 算例分析
本文在2个系统上实施了上述的规划方法。系统A是IEEE标准39节点测试网络,包含有10发电机、39节点以及17异步电机。系统B是广东省级电网,包含有181发电机、1 009节点以及361异步电机。本章的算例计算是在一台高性能服务器上完成的,它具有16组Dell M620刀片机,每个刀片又配有2个Xeon E5- 2650处理器(其中每个处理器都是8核8线程)和128 GB的运行内存。计算平台分别采用GAMS 24.4.6做优化计算[16],MATLAB 2015a 做编程,以及PSD-BPA做时域仿真[17]。在上述2个测试系统上进行N-2扫描,分别获得6个短期电压失稳的故障组成故障集。以下STATCOM的布点和容量规划将解决故障集导致的短期电压失稳问题。
首先以系统A为例子,把本文的规划方法对比传统的布点及容量完全割裂的规划方法,即先通过灵敏度计算确定安装地点再确定安装容量。经过计算,表2列举了本文的布点和容量统一规划方案,共需6台STATCOM,配置总容量为286.52 Mvar。表3列举了传统的布点及容量完全割裂的规划方案,同样需要6台STATCOM共338.68 Mvar。由2个表格可看出,虽然两个方案需要的STATCOM数量即布点数相同,但本文的布点和容量统一规划方案需要的容量和费用远小于传统的规划方法,因此更加经济,是安装地点和安装容量整体的最优结果;而传统的做法仅仅只是安装地点和安装容量的分别最优。

表2 本文的布点和容量统一规划方案Tab.2 Unified plan of location and capacity in this paper Mvar
STATCOM的规划难点在于混合整数规划。有学者指出,如果全体负荷母线均为STATCOM备选安装点,只规划STATCOM容量,即可避免混合整数规划问题。然而,该方法只能最小化容量的规划,却无法记及STATCOM的固定安装费用c1。STATCOM总体投资费用变得很大,因为几乎所有母线都规划安装STATCOM。
同样以系统A为例,如果所有负荷点均为STATCOM的规划节点,以此极小化STATCOM的规划容量。该规划方案列举在图1中,在17个负荷

表3 传统的布点及容量完全割裂的规划方案Tab.3 Conventional separated plan of location and capacity Mvar
节点的规划容量共219.28 Mvar,略小于表2即本文方案的286.52 Mvar。但是,图1的规划方案中,规划容量被分散到17台STATCOM,数量较大,因此基建费用较高。对应的STATCOM规划费用是32 716.52 万元,远高于表2的方案20 691.087 万元。因此在实际运行中,南方电网较多情况是集中安装少量的大容量STATCOM以减少基建费用,提高投资的效率。
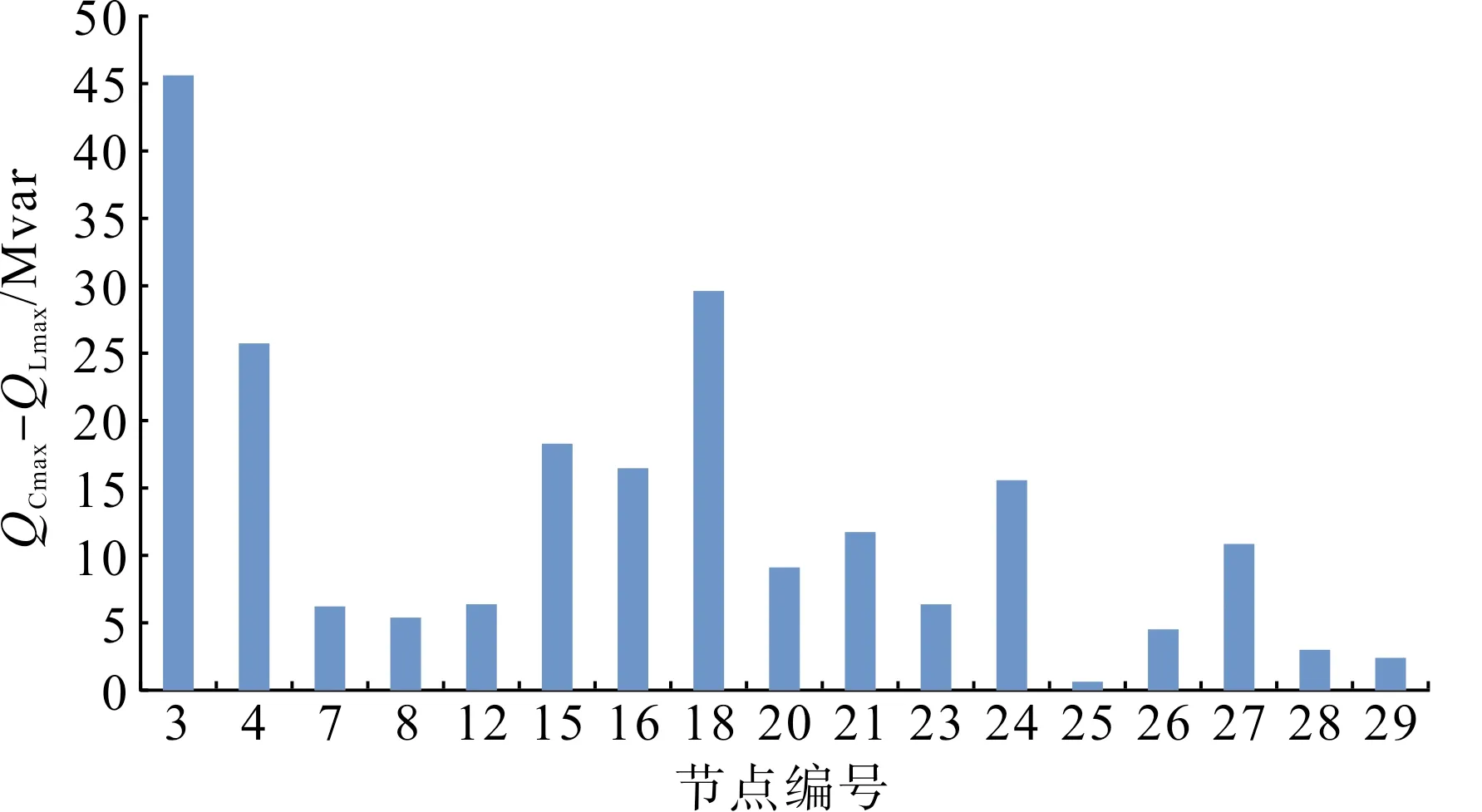
图1 STATCOM在所有负荷节点的规划容量Fig.1 Capacities of STATCOM at all of the loads
为了验证本文凸松弛方法的正确性,系统A作为公共可用的IEEE测试系统,其算例用于案例的比较和复现。传统的布点及容量完全割裂的规划方法或者标准求解器,在涉及大型实际电网案例时会面临巨大的求解压力;相反,它们可以快捷地求解系统A类的测试系统,并提供相应的计算结果,作为凸松弛方法的对比。在另一方面,系统B作为一个实际省级电网,其算例可验证凸松弛方法求解STATCOM布点及容量规划问题的高效性。在此算例上,凸松弛方法在可接受的时间框架内可获取STATCOM规划问题的方案,然而像SBB这种求解器却不能完成,足以验证凸松弛方法的高效性。
如图2所示,系统B在故障集下节点电压恢复缓慢,大量节点在故障清除1 s后仍然不能恢复0.75 p.u.以上,短期电压失稳。采用本文凸松弛算法计算获得的STATCOM规划方案如表4所示。在该规划方案下,如图3所示,系统B能够恢复短期电压安全。

图2 系统B在故障集下的电压轨迹Fig.2 Voltages of system B under contingency set

表4 系统B的STATCOM规划方案Tab.4 Planning of STATCOM for system B

图3 含STATCOM规划的系统B在故障集下的电压Fig.3 Voltages of system B under contingency set with planning of STATCOM
针对混合整数规划,目前存在成熟的商业求解器SBB。SBB求解器是GAMS平台上其中一种较为流行和通用的混合整数非线性规划求解器。SBB结合了求解混合整数线性规划的分支定界(branch and bound,B&B)方法以及某些标准的非线性规划求解器(可供用户选择)如MINOS、SNOPT。在求解混合整数非线性规划问题时,SBB先对整数规划部分实施分支定界,求取一个相对较好的整数规划结果,然后再基于用户选择的非线性规划求解器对非线性规划部分实施求解,从而获得混合整数非线性规划的结果。笔者在从事混合整数非线性规划问题研究的时候,先后比较过BARON、DICOPT、SBB等混合整数非线性规划求解器,最后发现SBB求解器对于本文的STATCOM布点及容量规划问题具有较好的求解效果。因此,文章最后将本文的凸松弛方法和SBB求解器的结果进行对比,以便验证本文方法的有效性和高效性。如表5展示了本文规划方法与SBB求解器的结果对比。

表5 本文方法和SBB求解器计算结果的比较Tab.5 Comparison of the results between the method in this paper and the SBB solver
在规模比较小的系统A中,凸松弛方法与SBB求解器的STATCOM整体规划费用基本一致,相差无几,因此本文的规划方案是可靠的。并且,本文凸松弛方法的计算时间远短于SBB求解器,说明凸松弛方法的求解效率更高。面对大规模系统B的STATCOM规划,SBB求解器需要求解大型混合整数规划问题,在花费较长时间后仍然不能获得STATCOM的规划方案。整数规划问题可以理解为组合优化问题,而组合优化问题的规模随着控制变量数量的增加呈现指数增长,极其容易引发数学上的指数爆炸问题。对于实际1 009节点系统B的规划问题,由于节点数量庞大,其控制变量(包括STATCOM的规划容量和安装地点)的数量也相应非常大。一般而言,当控制变量的数量大于20,组合的数量已经超过百万。如此庞大的组合数量,在上述分支定界的过程要存储很多分支和叶子节点,花费很多内存空间。分支定界法的求解效率基本上由值界方法决定,若界估计不好,在极端情况下将与穷举搜索没多大区别,在有限的时间内不能计算所有的组合。因此,面对1 009节点系统B,SBB求解器不能获得最优解,其本质原因是变量的数量太大,同时组合数量指数式增长,出现了整数规划的指数爆炸问题。但凸松弛方法不需要直接求解混合整数优化,只需要求解连续的优化问题。许多经典的基于梯度的优化方法,如内点法,可以轻松获得最优解,因此凸松弛方法在系统B仍然得到了最优的规划方案。因此,本文的规划方法更适用于南方电网的STATCOM规划。
5 结语
本文针对受端电网STATCOM的布点和容量规划问题,采用了布点和容量统一规划的混合整数规划模型,并提出了一种针对混合整数规划的凸松弛方法。该方法首先关于整数变量整体凸化混合整数规划模型,然后对凸模型实施一种紧松弛,避免直接求解混合整数规划。
在IEEE标准39节点以及广东电网的算例计算表明,该方法比传统的割裂布点和容量的规划方法的STATCOM投资费用更小。布点和容量同时规划的必要性得到了验证。相比商业化的求解器SBB,本文凸松弛方法更适用于在大型受端电网如广东电网的STATCOM规划问题,因求解效率更高,计算时间更短,容易获得大规模规划问题的最优解。

