《空间平行关系》教学设计

马明宇

教学目标

1.知识与技能目标：通过观察模型，使学生进一步理解并掌握空间线线、线面、面面间的平行关系的判定与性质有关知识，探究三者之间的相互转化，并能正确选择定理进行证明。

2.过程与方法目标：经历从模型演示中抽象出几何图形和几何问题的过程，感受线线、线面、面面间平行的直观感觉，进一步培养和发展学生的几何直觉，培养学生运用图形语言进行交流的能力，空间想象能力。在学生经过观察实验猜想等合情推理活动后，再进行演绎推理和逻辑论证，进而培养学生逻辑推理论证能力。

3.情感、态度、价值观目标：由几何画板呈现的规范的几何图形和例题的板书中，体会数学图形的对称美、证明过程的简洁美，不断提高学习数学的兴趣，树立学好数学的信心，并养成严谨、缜密的思维习惯，形成锲而不舍的钻研精神和科学态度。

教学重难点分析

空间线线、线面、面面平行关系的转化。线面平行的各种判定方法。

而由线//线推证线//面时找辅助线、由面//面推证线//面时找辅助面正是本节课的难点，是要重点突破的问题。

教学过程：

一、导入新课：开门见山，以简单问题带动。

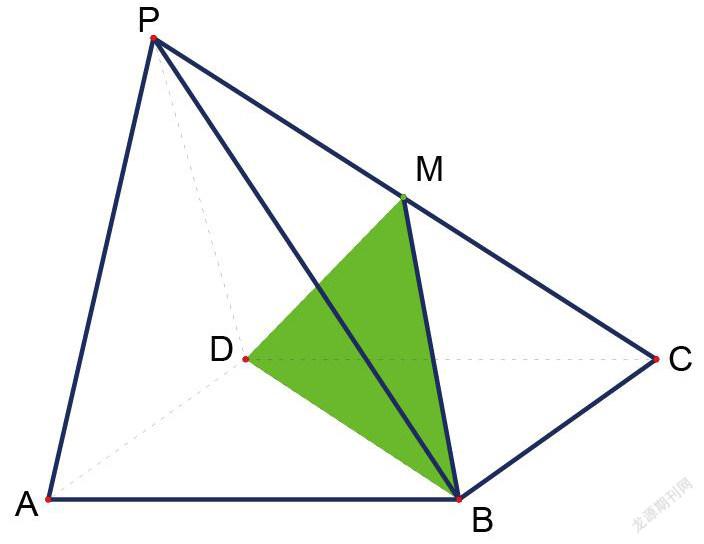
已知四棱锥P-ABCD的底 面ABCD为平行四边形，点M在PC上，

（1）若M为PC的中点，求证：PA//平面MBD

（2）PA//平面MBD，求证：M为PC的中点

【设计意图】是“低梯度”“低起点”的线面平行的证明题，中位线 平行”推理形式的类型是学生常見的“中点既可以巩固知识点（线面平行的判定定理及性质定理），又可使学生轻轻松松进入后续学习。为学生的思维活动热身，也为学生的后续学习“开窍”，使学生能体验初次探究的乐趣

二、典型例题解析

通过模型演示（对空间图形进行感性认识），抽象出几何问题：

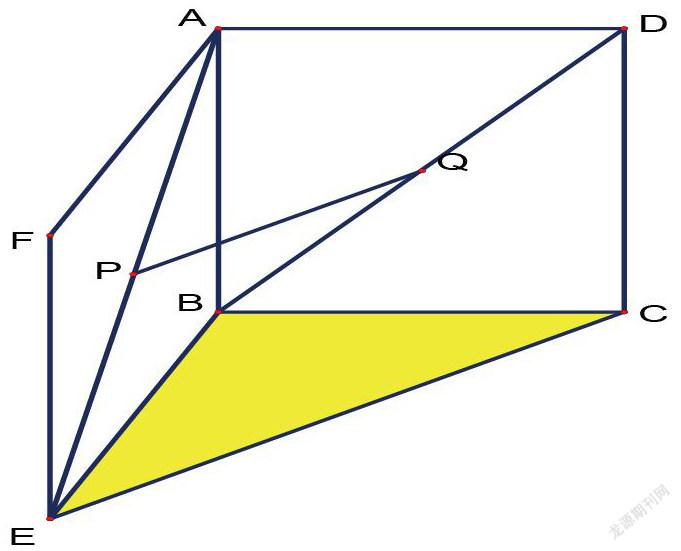
例 已知有公共边AB的两个全等矩形ABCD和ABEF不同在一个平面内，点P在对角线AE上，点Q在对角线BD上。

（1）若P、Q分别是AE、BD的中点，求证：PQ//平面BCE

（此问由学生独立完成）

【设计意图】识别图形，建立直观感觉。进一步熟悉线面平行判定定理。

变式：（2）M、N分别是AE、AC上的点，且AM=AN。

求证：MN//平面BCE

（此问仍由学生独立完成，教师稍做点拔。）

【设计意图】体会连结AQ并延长构造三角形对证明过程所起的关键作用，进而为下一题的解决做铺垫。

变式：（3）若AP=DQ，求证：PQ//平面BCE

（此题经由教师点拔、学生相互合作、交流共同完成）

【设计意图】识别图形，建立直观感觉。进一步熟悉线面平行判定定理。

变式：（2）M、N分别是AE、AC上的点，且AM=AN。

求证：MN//平面BCE

（此问仍由学生独立完成，教师稍做点拔。）

【设计意图】体会连结AQ并延长构造三角形对证明过程所起的关键作用，进而为下一题的解决做铺垫。

三、深化认识，总结规律

（投影）请同学们根据上述例题，在独立思考的基础上（必要时可以小组讨论），总结学到的知识。

教学效果：

这节课能较好完成教学任务，学生能基本掌握空间中平行关系的证明方法，特别是例题能较好达到如期效果，整节课上，学生的思维活跃，学生对如何寻找辅助线，这一难点能较好突破，但学生作图的基本功不够，虚线、实线的应用较混乱。

教学反思：

本节课的教学策略是先让学生观察、思考、分析典型例题，搜索已掌握的相关信息，归纳得出相应类型及其求解策略，再由老师进行思维点拨，再运用，这样培养了学生的数学思维，也充分体现了由特殊到一般，再由一般到特殊的数学思想。设计教学时考虑了由易到难，由浅到深，层层递进的思维模式;考虑了变式教学的有效性，充分体现了“以变应变，以变应新”的教学思想等。为了提高教学的有效性，在备课阶段，我认真的思考了该如何设置每一道习题，揣摩用什么样的语言能够让学生更好的接受，提什么样的问题既能调动学生的积极性又能达到我要引导学生发现的目的。想象着学生可能会出现的每一种解决问题的方式。因为经过课前充分的准备，认真的思考，对细节仔细的推敲，分析学生的每一种想法和课堂上可能出现的各种问题。所以在课上，学生们充分发挥自己的优势，说出各种想法，真正的实现学生是课堂的主体。

当然，本节课还有一定的不足，在总结所学的知识点时，没有给学生更多的讨论空间，还有部份学生不能准确提炼出证明方法。