高强钢-铝合金材料的流动应力模型研究及应用

李奇涵，王宝中，高嵩，徐传伟，马风雷，韩小亨，袁博

高强钢-铝合金材料的流动应力模型研究及应用

李奇涵1，王宝中1，高嵩1，徐传伟1，马风雷1，韩小亨1，袁博1

（长春工业大学 机电工程学院，长春 130012）

研究常温下无铆连接中高强钢与铝合金材料的应力-应变关系以及本构模型的预测效果。通过拉伸试验初步研究材料性能，主要包括屈服强度、拉伸强度和伸长率等；然后采用4种流动应力模型描述塑性段，即本构模型，分别对两种材料的应力-应变关系进行表述。随后采用相关系数值和平均绝对相对误差AARE值评价4种模型预测应力的效果。4种本构模型均能够较好地描述两种材料的应力-应变关系，高强钢与铝合金材料拟合后的值高于0.99，AARE值低于2%。通过对比分析，Voce模型表述高强钢材料应力-应变关系的效果更好，Swift模型表述铝合金材料应力-应变关系的效果更好，并成功应用于无铆连接工艺中，且误差均低于5%。

高强钢；铝合金；拉伸试验；本构模型；无铆连接

随着轻量化技术的发展，钢、铝材料以良好的塑性加工性能广泛应用于车身设计与制造领域，且钢-铝混合车身的结构也越来越多应用于汽车设计与制造中。文中针对6061-T6铝合金和HC340/590DP双相高强钢的无铆连接[1—3]问题开展研究，通过拉伸试验分析两种材料的性能，绘制应力-应变曲线，但描述其性能不能仅限于应力-应变曲线。为了进一步表述材料应力-应变关系，文中建立了合理的流动应力模型。常见的模型主要包括J-C，Swift，Ludwik，Voce，Z-H等。专家学者们大多采用优化材料参数的方法来精确描述特定材料的塑性[4—6]；修正单一的本构方程来获得更优的拟合精度[7—11]，使其更加贴合试验数据；通过多种本构方程的比较，选择适用范围更广泛的模型[12]。Li等[13—14]通过比较多级串、并联或优化多种参数的方式，更好地获得了预测钢铝材料流动应力的本构方程。

文中以6061-T6铝合金和HC340/590DP双相钢为研究对象，以拉伸试验为基础，获取材料的基本力学性能，并采用Swift，Voce，J-C，Ludwid这4种流动应力模型分别表述高强钢和铝合金材料的应力-应变关系，并对各个模型的拟合效果进行分析和评价。分别获得适用于表述高强钢和铝合金材料的应力-应变关系的最佳模型，两种材料拟合后的值高于0.99，AARE值低于2%。流动应力模型成功应用于无铆连接数值模拟中，且颈厚值的预测误差为0.6%，嵌入值的预测误差为2.8%，数值模拟的预测效果较好。

1 材料性能

1.1 基本力学性能

采用6061-T6铝合金和HC340/590DP双相钢，力学性能如表1所示。两种材料的力学性能差异较大，高强钢的弹性模量约为铝合金的3倍，屈服强度约为2倍，抗拉强度约为3倍。两者在相同的受力条件下，铝合金将首先进入塑性状态，这是由于铝合金是体心立方结构，滑移系较多能够通过滑移来协调变形，使其具有较好的延展性。

表1 材料的力学性能

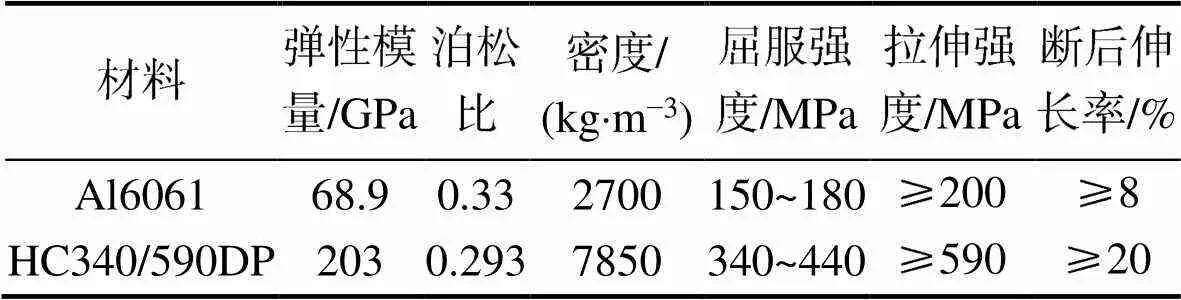
Tab.1 Mechanical properties of materials

1.2 拉伸试验设备及试样

采用单向拉伸试验来测定材料的力学性能，试样采用国家标准，如图1所示，拉伸试样的厚度为2 mm，标距为35.73 mm。试验设备选用WDW-100E微机控制电子万能试验机（最大拉力为100 kN，最大行程为600 mm）。应变速率需要根据各个工艺的实际成形速率进行选取，文中选取的应变速率分别为0.001，0.005，0.01，0.05，0.1 s−1。其中在应变速率为0.05 s−1时，对各个模型进行了评价。

图1 上铝下钢接头的截面

2 结果与分析

根据所选的不同应变速率，钢、铝试样分别分成5组进行拉伸，每组试验做3次，取平均值作为该组的实际值。铝试样的断裂口为倾斜，钢试样的断裂口为横向水平，其中应变速率为0.05 s−1时断裂口最为标准。根据拉伸力、位移、时间、变形量等数据，计算两种材料在不同应变速率下的真实应力-应变曲线，如图2所示。从两种材料在不同应变速率下的抗拉极限变化趋势来看，钢、铝的抗拉极限受到应变速率的影响，铝合金材料随着应变速率的增大，抗拉极限减小；高强钢材料随着应变速率的增大，抗拉极限先增大后减小。

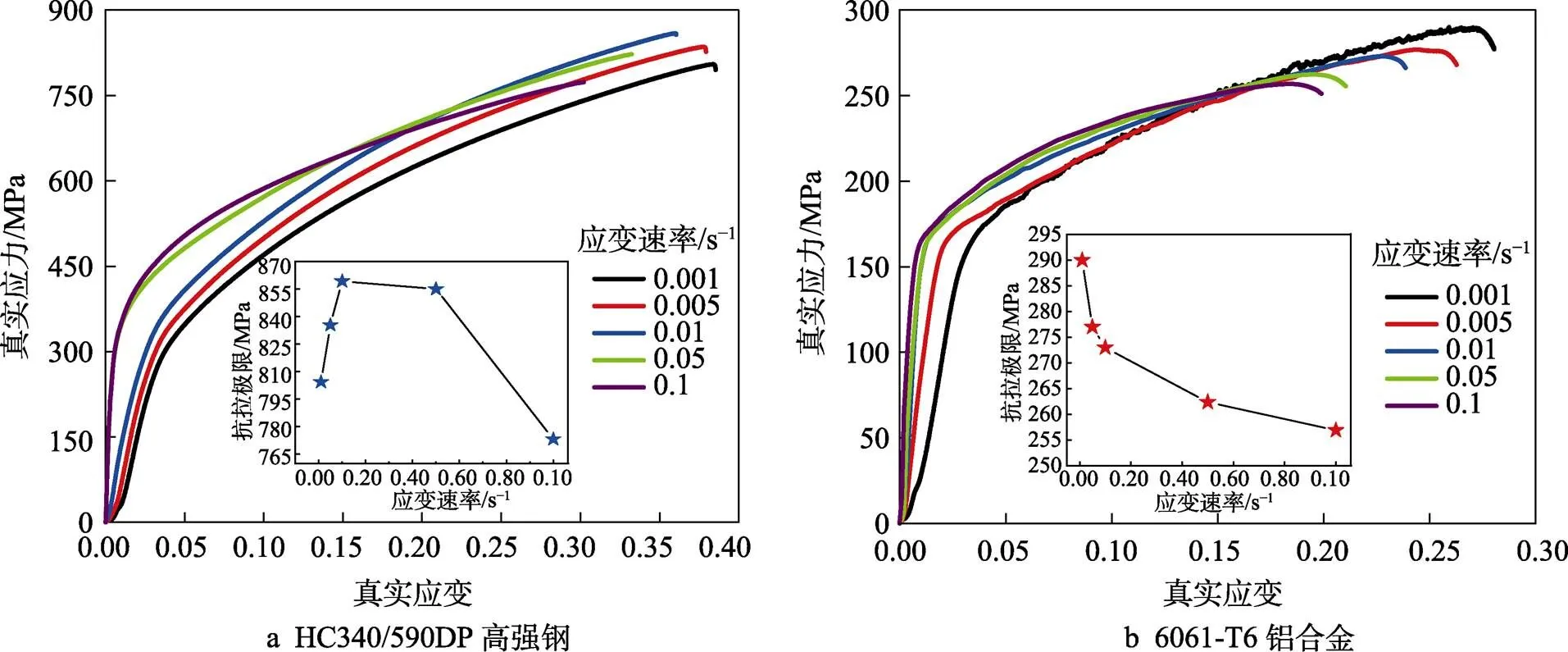
图2 不同应变速率下真实应力-应变曲线

3 流动应力模型分析及选取

3.1 模型的相关介绍

采用4种塑性段流动应力模型来表述拉伸试验的结果，即应力和应变之间的关系，主要包括Swift模型、Voce模型、Johnson-Cook模型和Ludwik模型，其主要公式如下：

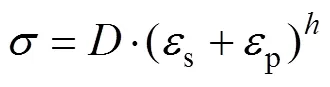
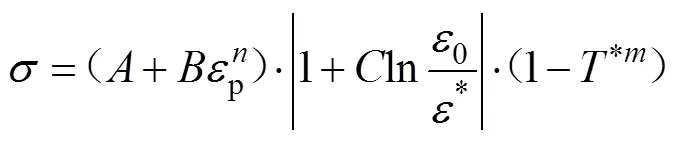
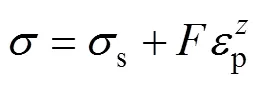
式中：为材料的流动应力；p为等效塑性应变；s为屈服应变；s为屈服应力；，，，均为材料的硬化系数；，，，为硬化因数；和为材料常数；为选定应变速率下的屈服应力；0为选定的应变速率；*为参考应变速率，本次不涉及高温，所以1−*不做相关介绍。

3.2 拟合方法及结果评价

根据以上4种模型，结合试验数据分别对材料参数进行计算，然后进行线性拟合，求得对应的材料参数，钢、铝材料的4种模型拟合参数结果如表2所示。

表2 材料参数的拟合结果

Tab.2 Fitting results of material parameters

将钢、铝材料的等效塑性应变分别带入拟合完成后的4种模型中，取其中的等间距数据点与拉伸试验数据进行对比，其结果如图3所示。图3a表示高强钢材料与试验的对比结果，图3b表示铝合金材料与试验的对比结果。根据所获得的试验应力值和4种模型的预测应力值，进行相关评价，公式如下：

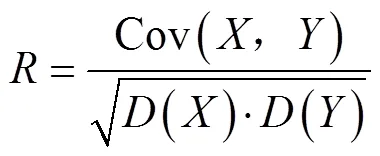
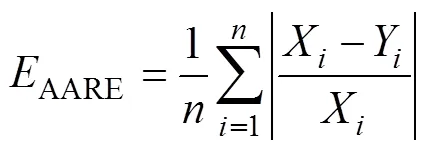
式中：为相关系数；表示拉伸试验获得的流动应力的数组；表示模型预测的流动应力的数组；表示数组中数据点的数量；AARE表示平均绝对相对误差。分别将两组数据求方差和数学期望，代入式（5），可得该模型的相关系数，相关系数表征了变量和的密切程度，和是正相关，因此值越大，模型的预测数据与试验数据的线性关系越密切，相关程度越好。AARE也能反映两种变量的相关程度，与相关系数配合分析4种模型的预测效果。

高强钢材料在拟合后对不同模型的评价指标如图4所示，4种模型的数据点均集中落在最佳线性拟合直线附近，且值分别为0.999 427，0.999 506，0.996 846，0.996 578。其中Swift模型和Voce模型的值较大，预测效果较好；另一方面高强钢材料的数据点与点划线都有两个交点，交点表示误差为0，Swift模型和Voce模型误差较大的数据点较少，且AARE值分别为0.643%和0.451%，预测效果较好，而J-C模型和Ludwik模型存在一些误差较大的数据点，AARE值分别为1.376%和1.728%，预测效果相对较差。

铝合金材料在拟合后对不同模型的评价指标如图5所示，4种模型的数据点均集中落在实线附近，值分别为0.999 324，0.995 797，0.991 518，0.991 686，且Swift模型的值较大，预测效果较好；另一方面铝合金材料的各个模型的数据点与点划线都有两个交点，Swift模型有3个交点，且Swift模型误差较大的数据点较少，AARE值为0.307%，预测效果较好，而Voce模型、J-C模型和Ludwik模型存在一些误差较大的数据点，AARE值分别为0.847%，1.227%和1.296%，预测效果相对来说差一些。

图3 试验与材料模型的对比

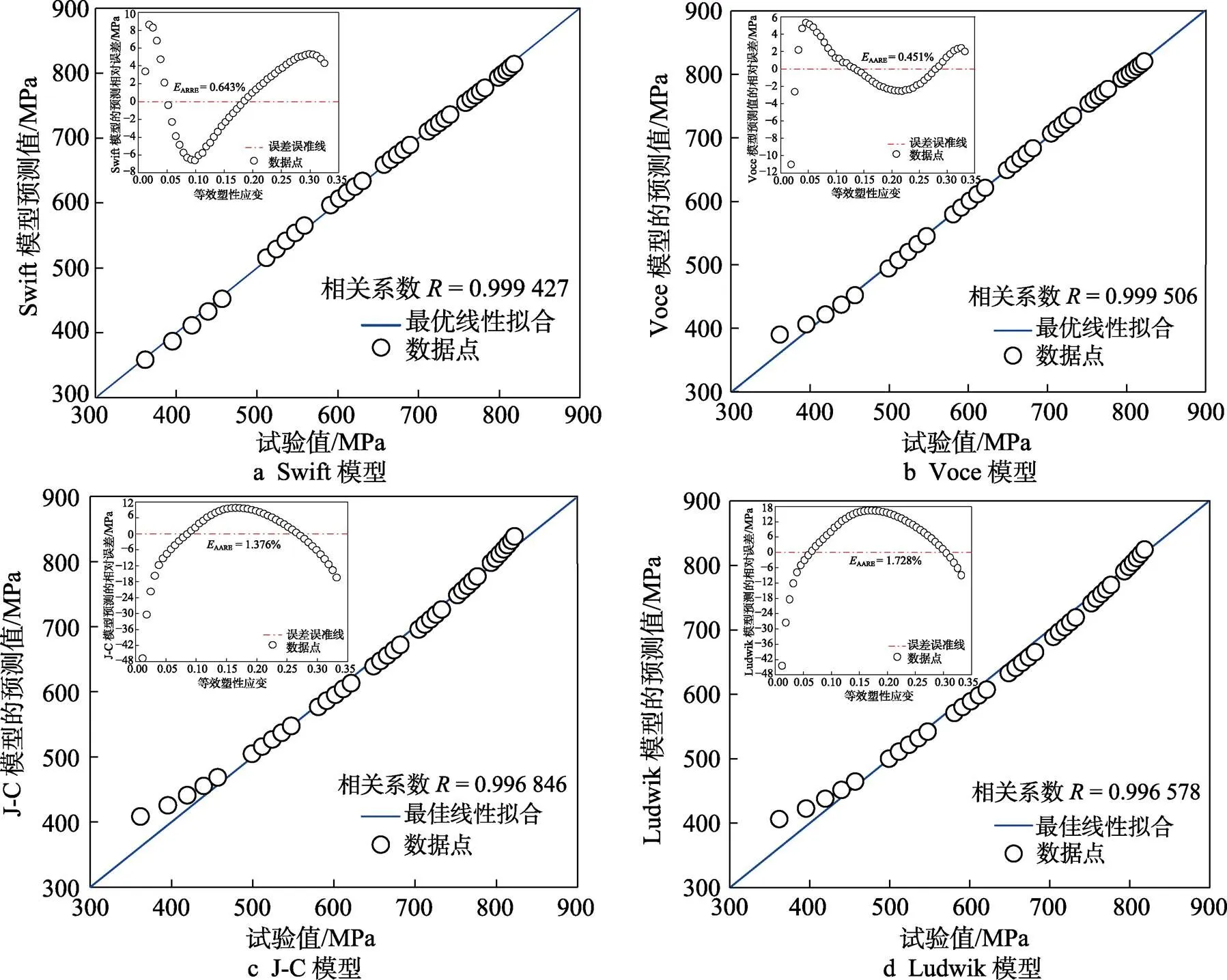
图4 高强钢材料模型的预测应力值与试验的相关性

图5 铝合金材料模型的预测应力值与试验的相关性

4 流动应力模型在无铆连接中的应用

数值模型和试验模具如图6所示，试验采用CEC08型落地冲压机，被连接板料在凸凹模共同作用下发生弹塑性变形，从而形成自锁结构，因无铆连接过程满足完全轴对称条件，为提高计算效率，采用1/2平面模型进行建模，定义固支边界条件，材料定义为可变形体，网格单元采用C3D8X，冲程为3.6 mm，压边力为15 kN，模具与板材间的摩擦因数为0.12，板材间的摩擦因数为0.28。将上述模型的选取结果进行无铆连接仿真分析，并与试验对比，如图7所示，接头成形后有两个关键尺寸参数（颈厚值、嵌入值），试验得到的颈厚值和嵌入值分别为0.325 mm和0.249 mm，模拟结果为0.327 mm和0.242 mm。结果表明，颈厚值的预测误差为0.6%，嵌入值的预测误差为2.8%，数值模拟的预测效果较好，误差低于5%，因此，流动应力模型可以有效地应用于无铆塑性连接数值模拟中。

图6 数值模型与试验模具

图7 数值模拟结果与试验结果对比

5 结论

根据拉伸试验，建立了高强钢与铝合金材料的本构模型，即Swift模型、Voce模型、J-C模型及Ludwik模型，并分别通过值和AARE值评价了4种模型对两种材料流动应力的预测效果，具体结论如下。

1）通过拉伸试验，获得了HC340/590DP高强钢和6061-T6铝合金的基本力学性能。

2）采用4种塑性段的本构模型描述了两种材料的应力-应变关系。

3）4种本构模型均能够较好地描述两种材料的应力-应变关系，其中高强钢与铝合金材料拟合后的值均高于0.99，AARE值均低于2%，且Voce模型表述高强钢的应力-应变关系的效果更好，Swift模型表述铝合金的应力-应变关系的效果更好，并成功应用于无铆连接工艺中，且误差低于5%。

[1] GE Y, XIA Y. Mechanical Characterization of a Steel-Aluminum Clinched Joint under Impact Loading[J]. Thin-Walled Structures, 2020, 151: 106759.

[2] HUANG Z, YANAGIMOTO J. Dissimilar Joining of Aluminum Alloy and Stainless Steel Thin Sheets by Thermally Assisted Plastic Deformation[J]. Journal of Materials Processing Technology, 2015, 225: 393—404.

[3] LEE C J, LEE J M, RYU H Y, et al. Design of Hole-Clinching Process for Joining of Dissimilar Materials-Al6061-T4 Alloy with DP780 Steel, Hot-Pressed 22MnB5 Steel, and Carbon Fiber Reinforced Plastic[J]. Journal of Materials Processing Tech, 2014, 214(10): 2169—2178.

[4] CAI J, LI F G, LIU T Y, et al. Constitutive Equations for Elevated Temperature Flow Stress of Ti-6Al-4V Alloy Considering the Effect of Strain[J]. Materials and Design, 2010, 32(3): 1144—1151.

[5] RUDNYTSKYJ A, SIMON P, JECH M, et al. Constitutive Modelling of the 6061 Aluminium Alloy under Hot Rolling Conditions and Large Strain Ranges[J]. Materials & Design, 2020: 108568.

[6] 潘应晖, 戴峰泽, 鲁金忠. 激光冲击Johnson-Cook模型材料参数优化[J]. 兰州理工大学学报, 2012(2): 15—18. PAN Ying-hui, DAI Feng-ze, LU Jin-zhong. Optimization of Material Parameters for Johnson Cook Model of Laser Shock[J]. Journal of Lanzhou University of Technology, 2012(2): 15—18.

[7] SEO S, MIN O, YANG H. Constitutive Equation for Ti-6Al-4V at High Temperatures Measured Using the SHPB Technique[J]. International Journal of Impact Engineering, 2005, 31(6): 735—754.

[8] LIN Y C, CHEN X M, LIU G. A Modified Johnson-Cook Model for Tensile Behaviors of Typical High-Strength Alloy Steel[J]. Materials Science & Engineering A, 2010, 527(26): 6980—6986.

[9] 聂振超, 刘光连, 刘曦程, 等. 试验研究Q345钢和20Cr13合金应变硬化关系曲线[J]. 塑性工程学报, 2018, 25(1): 233—240. NIE Zhen-chao, LIU Guang-lian, LIU Xi-cheng, et al. Experimental Study on Strain Hardening Curve of Q345 Steel and 20cr13 Alloy[J]. Journal of Plastic Engineering, 2018, 25(1): 233—240.

[10] 李贤睿, 方文利, 唐鼎, 等. 铝合金微通道扁管热挤压成形数值模拟[J]. 塑性工程学报, 2017, 24(5): 1—6. LI Xian-rui, FANG Wen-li, TANG Ding, et al. Numerical Simulation of Hot Extrusion Forming of Aluminum Alloy Microchannel Flat Tube[J]. Journal of Plastic Engineering, 2017, 24(5): 1—6.

[11] 陈水生. 基于硬度积分中值的拼焊板焊缝力学性能确定[J]. 塑性工程学报, 2016, 23(4): 160—163. CHEN Shui-sheng. Determination of Mechanical Properties of Tailor Welded Blanks Based on Median Value of Hardness Integral[J]. Journal of Plastic Engineering, 2016, 23(4): 160—163.

[12] WANG Lei, BENITO J A, CALVO J, et al. Constitutive Model of TWIP Steel after Multi Pass Equal Channel Extrusion[J]. Journal of Material Heat Treatment, 2017, 38(2): 185—190.

[13] JIA F, LI F, LI Y. Characterization and the Improved Arrhenius Model of 0Cr11Ni2MoVNb Steel during Hot Deformation Process[J]. IOP Conference Series: Materials Science and Engineering, 2018, 382(2): 022027.

[14] 李攀, 李付国, 曹俊, 等. 基于修正DMNR模型的1060纯铝本构方程[J]. 中国有色金属学报(英文版), 2016, 26(4): 1079—1095. LI Pan, LI Fu-guo, CAO Jun, et al. Constitutive Equation of 1060 Pure Aluminum Based on Modified Dmnr Model[J]. Chinese Journal of Nonferrous Metals, 2016, 26(4): 1079—1095.

Study on Flow Stress Model of High-Strength Steel and Aluminum Alloy in Clinching

LI Qi-han1, WANG Bao-zhong1, GAO Song1, XU Chuan-wei1, MA Feng-lei1, HAN Xiao-heng1, YUAN Bo1

(Changchun University of Technology, Changchun 130012, China)

This paper aims to study the stress-strain relationship between high-strength steel and aluminum alloy in clinching at room temperature. The materialʹs properties were studied through the tensile test, including yield strength, tensile strength, and elongation. Then, four flow stress models, namely the constitutive model, were used to describe the stress-strain relationship of the two materials. Then the correlation coefficientand average absolute relative errorAAREwere used to evaluate the effect of the four models. The results show that the four constitutive models can well describe the stress-strain relationship of the two materials. The-value of high-strength steel and aluminum alloy is higher than 0.99, and theAAREvalue is lower than 2%. Through comparative analysis, Voce model is more effective to describe the stress-strain relationship of high-strength steel, and the Swift model is more effective to describe the stress-strain relationship of aluminum alloy. It is successfully applied to the clinched process, and the error is less than 5%.

high strength steel; aluminium alloy; tensile test; constitutive model; clinching

10.3969/j.issn.1674-6457.2021.04.017

TU502

A

1674-6457(2021)04-0121-06

2021-04-26

吉林省科技发展计划（20190302100GX）；国家自然科学基金（51805045）

李奇涵（1970—），男，博士，教授，主要研究方向为金属板料冲压成形技术。