Ni- Al二元合金γ相高温点阵常数及热膨胀系数的试验与计算研究

王治超 鲁晓刚 朱娜琼

(1. 上海大学材料科学与工程学院，上海 200444； 2.上海大学材料基因组工程研究院，上海 200444；3.上海第二工业大学高等职业技术(国际)学院，上海 201209)

镍基高温合金由于γ′相(L12结构)对γ基体相(FCC结构)的强化作用，具有极优异的高温性能，能服役于静态、疲劳及蠕变等严苛工况，被应用于陆上燃气轮机、航空发动机及涡轮叶片等重要部件[1- 4]，受到了广泛关注。

点阵常数是金属材料的基本性质之一，也是影响镍基合金高温性能的重要参数。通过试验测定或计算预测较宽温度范围内镍基高温合金中γ及γ′相的点阵常数，对于镍基高温合金的优化设计及性能改善具有重要意义。

众多学者对镍基多元合金中γ及γ′相的点阵常数及热膨胀系数(CTE，coefficient of thermal expansion)展开了计算与试验研究[5- 10]。针对Ni- Al二元合金系，Bøttiger等[11]使用磁控溅射法制备了Ni- (3～31)Al(原子分数，%，下同)合金薄膜，并通过高温X射线衍射法测定了合金室温至280 ℃范围的点阵常数。Ayub等[12]采用X射线衍射法测定了分别于150、220、260、400和700 ℃时效1 h后油淬的Ni- 5Al合金γ相的室温点阵常数。Kamara等[13]采用X射线衍射法测定了于700 ℃时效168 h后水淬的Ni- 17.7Al合金在20～678 ℃范围内γ相的点阵常数。Kim等[14]考虑振动和热电子贡献，探究了元素对γ- Ni和γ′- Ni3Al热膨胀系数的影响，并结合计算数据、合金成分及相成分，预测了Ni- Al基合金中γ及γ′相的热膨胀系数，结果与试验数据吻合较好。Wang等[15]采用CALPHAD方法建立了Ni- Al二元系中γ及γ′相点阵常数的唯象模型，该模型能够描述温度及合金成分对两相点阵常数的影响，基于Dupin等优化的Ni- Al二元系热力学数据库[16]及试验数据得到了两相点阵常数模型的参数，由此计算得到的点阵常数与试验数据吻合较好。但该模型仅参考了Kamara等[13]的一组高温试验数据。Kamara等研究的Ni- 17.7Al合金时效处理后为γ+γ′两相组织，而Wang等在优化过程中基于冻结成分(frozen composition)假设，认为Kamara等测得的各温度下γ相成分对应于该合金700 ℃时效时的平衡相成分，即Ni- 12Al。

由上述研究结果可知，精确测定γ相Ni- Al合金的高温点阵常数及热膨胀系数对提高计算和预测的准确度十分重要。但目前对Ni- Al二元合金γ相的试验研究多集中于室温或低温段，高温点阵常数及热膨胀系数的试验数据十分有限。因此，本文采用高温X射线衍射及热膨胀法测定了γ单相及γ+γ′两相Ni- Al合金中γ相的高温点阵常数及热膨胀系数随Al含量及温度的变化，以期为计算和预测镍基多元合金在较宽温度范围内的点阵常数/摩尔体积提供基础数据。

1 试验材料与方法

1.1 试样制备

图1为使用Thermo- Calc软件[17]，基于Dupin等的热力学数据库[16]计算获得的Ni- Al二元合金富Ni端相图，设计了γ单相1号、2号合金及γ+γ′两相3号合金，化学成分及热处理工艺如表1所示。按时效处理工艺不同，3号合金又分为3- 1号、3- 2号和3- 3号合金。

表1 合金的化学成分及热处理工艺

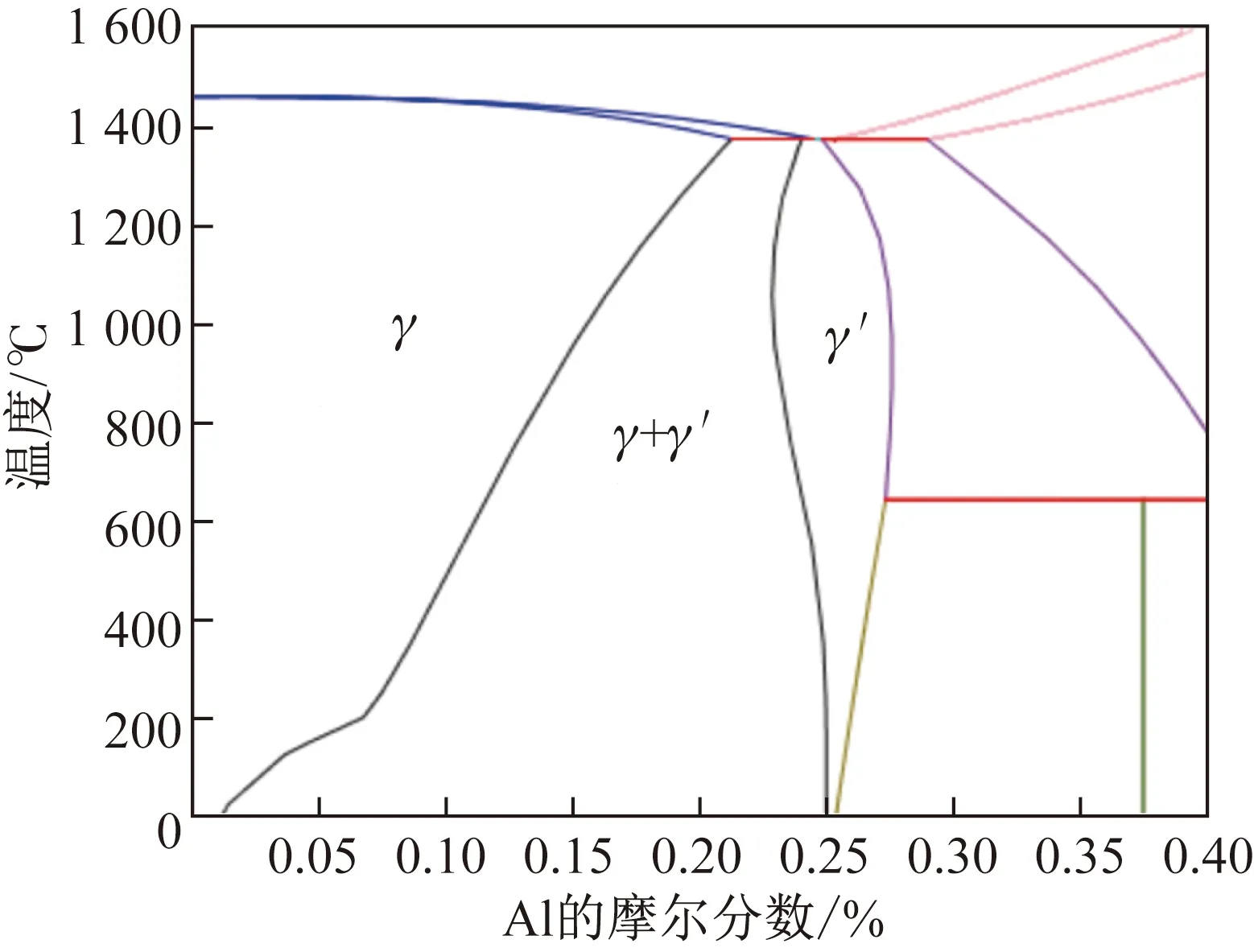
图1 Ni- Al二元合金相图

采用WK- Ⅱ型非自耗真空电弧熔炼炉熔炼合金，合金锭在熔炼过程中反复熔炼4次以确保均匀，然后封于充满氩气的石英管中，均匀化或时效处理后砸破石英管使试样直接水淬。

1.2 显微组织观察

将热处理后的试样经过机械研磨和抛光后进行化学腐蚀，腐蚀液为体积比2∶1∶1的硝酸、冰醋酸、水混合液，使用Leica DM 2700M型光学显微镜观察试样的显微组织。

1.3 热膨胀系数测定

采用DIL805A型热膨胀快速相变仪测定热膨胀系数，试样尺寸为φ4 mm×10 mm，于550 ℃退火处理24 h后炉冷，以去除线切割应力。

1号及2号合金试样的测温范围分别为200～900 ℃和550～900 ℃，根据相图(图1)，该温度区间合金处于γ单相区。试验时先将试样以50 ℃/min速率快速加热至测试温度附近，然后以10 ℃/min速率缓慢升温，测定试样长度L随温度T变化的膨胀曲线。

1.4 电子探针(EPMA)相成分测定

采用JXA- 8230型电子探针显微分析仪测定合金相组成，用点分析方法测定γ及γ′相的相成分。

1.5 点阵常数测定

用金刚石锉刀从热处理后试样上锉取粉末，在玛瑙研钵中研磨过筛后获得200～300目(54～74 μm)的粉末试样。将粉末包裹于钽片中封入石英管，1号及2号试样经550 ℃退火24 h后炉冷，3号试样经700 ℃退火24 h后炉冷，以去除研磨产生的应力。

采用Bruker D8 Advance型X射线衍射仪测定合金的高温X射线衍射图谱。测试过程中通入100 mL/min流量的高纯氩气，使用CuKɑ辐射，扫描角度为40°～80°，步进扫描，步长为0.1°，每步停留时间2 s，升温速率为10 ℃/min，测试前保温10 min。获得1号、2号试样在600、700、800及900 ℃，3号试样在700、800及900 ℃的高温X射线衍射图谱。采用Jade软件分析谱线获得合金在不同温度下γ相的点阵常数。

2 试验结果与分析

2.1 γ单相合金

2.1.1 显微组织

图2为1号和2号合金试样的显微组织，均为γ单相。

图2 1号(a)和2号(b)合金试样的显微组织

2.1.2 热膨胀系数

1号和2号合金试样的长度- 温度(L-T)曲线如图3(a)所示。本文假定热膨胀系数α随温度T呈线性变化，采用Origin软件对L-T曲线进行二次函数拟合(拟合得到Adj. R- Square分别为0.999 99和0.999 98)，根据式(1)计算获得试样的热膨胀系数- 温度(α-T)曲线，如图3(b)所示。

(1)

式中：L为试样长度；T为开氏温度。

由图3(b)可知，γ相的热膨胀系数随温度升高而增大，且含Al量较高的2号试样γ相热膨胀系数较大。

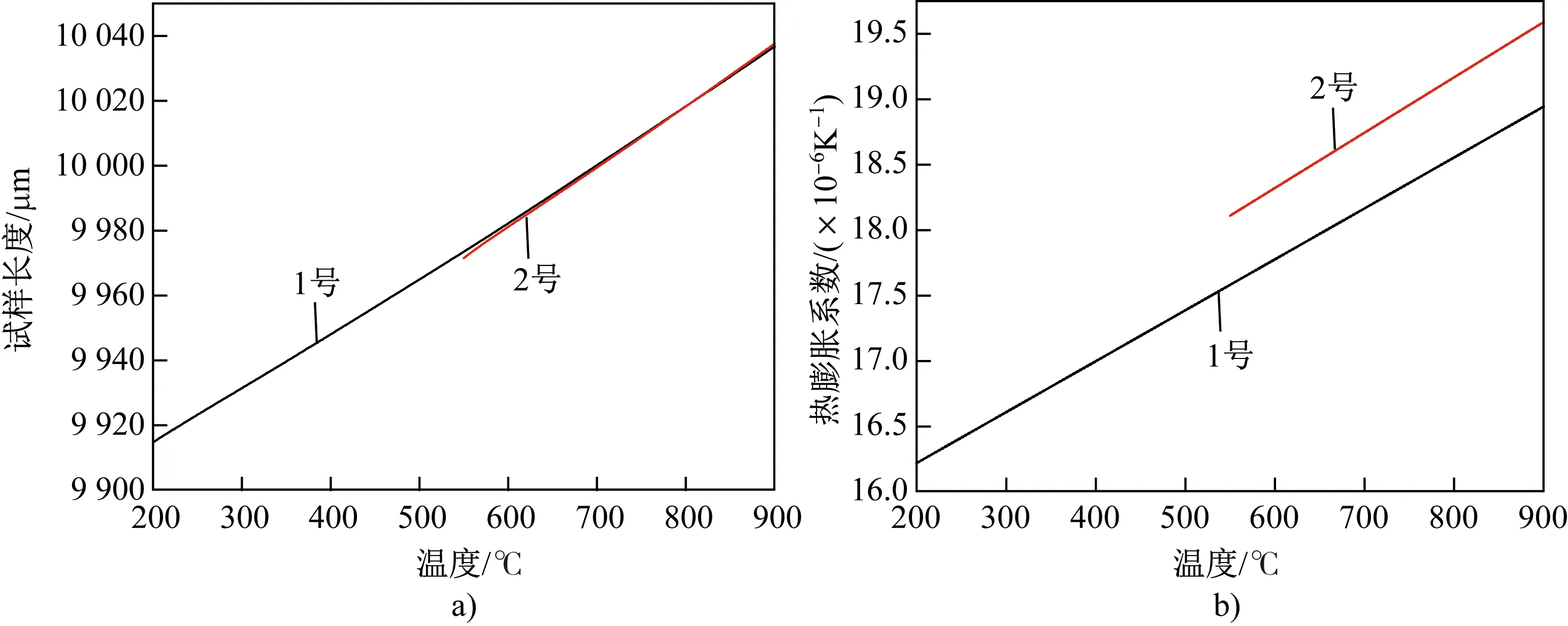
图3 合金试样的(a)长度和(b)热膨胀系数随温度变化的曲线

基于Wang等[15]的点阵常数模型计算得到1号和2号合金在不同温度下的点阵常数，同样根据式(2)计算获得由Wang等工作预测的热膨胀系数随温度的变化曲线。

(2)

式中a为γ相的点阵常数。

基于Kim等[14]的热膨胀系数模型计算得到1号和2号合金的热膨胀系数随温度的变化曲线，并将其及Wang等的计算结果与热膨胀仪测得的试验数据进行比较，如图4所示。由图4可见，试验测得的γ相热膨胀系数随Al含量的变化与Wang等的计算结果相吻合，即Al含量增加，热膨胀系数增大，但较Wang等的计算结果，试验测得的热膨胀系数随温度的变化趋势较缓。Kim等计算所得γ相热膨胀系数随Al含量的变化很小，相较而言，温度变化对其影响更大，含Al量较高的2号试样热膨胀系数的计算值较1号试样更小，与本文测定结果以及Wang等计算所得γ相热膨胀系数随Al含量的变化规律不符。

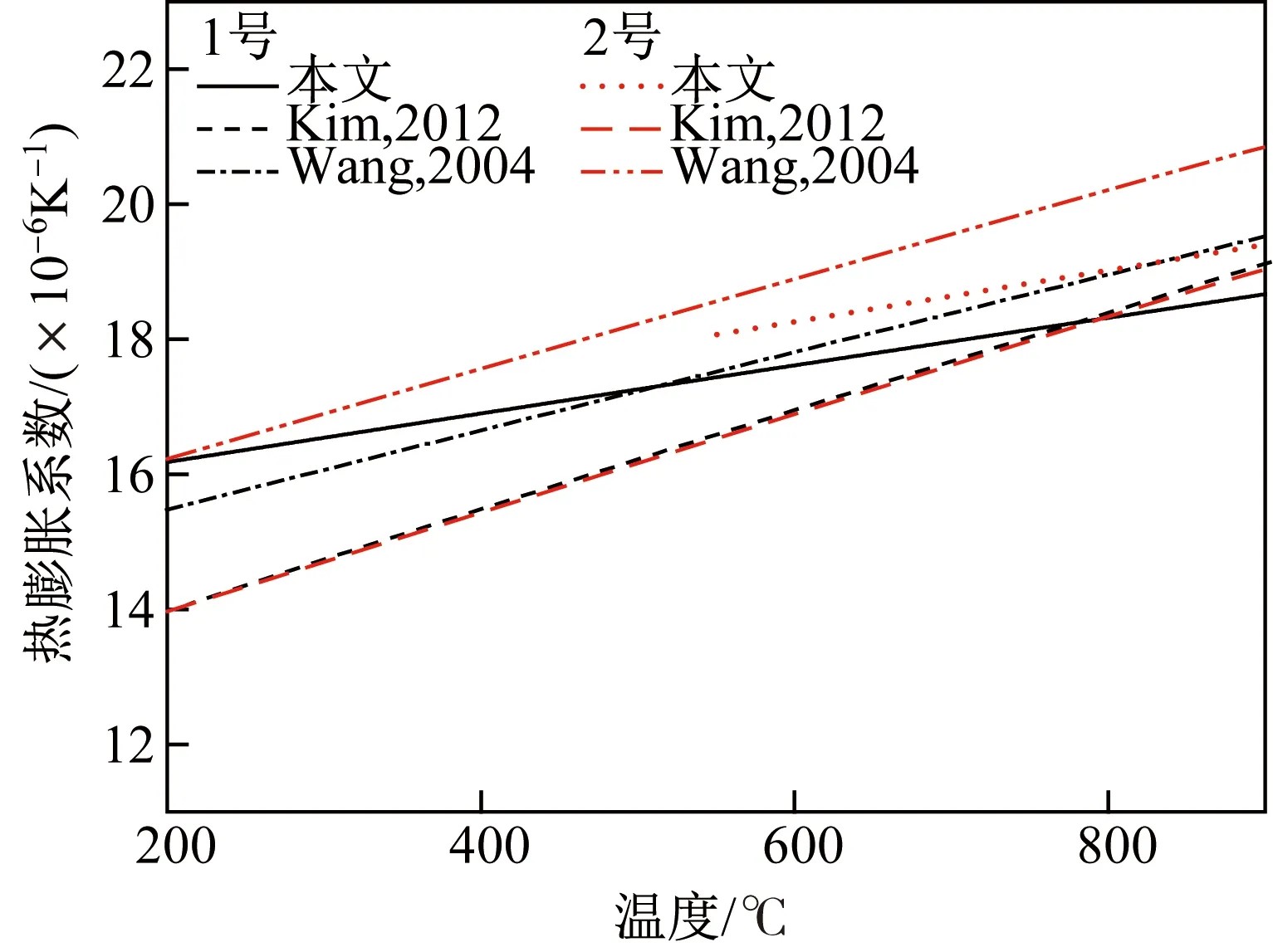
图4 试验测定的1号和2号合金试样热膨胀系数与Kim等[14]及Wang等[15]的计算结果

2.1.3 高温X射线衍射分析

图5为1号及2号合金试样在不同温度的X射线衍射图谱。由图可见，γ相的3个衍射峰(111)、(200)及(220)的峰位随温度升高向低角度偏移，这是γ相的点阵常数随温度升高而增大所致。采用Jade软件，选取峰型函数Pearson- VⅡ进行全谱拟合，经精修后得到合金在不同温度的γ相点阵常数。1号和2号合金试样在不同温度的γ相点阵常数、标准偏差及拟合残差如表4所示。

表4 1号和2号合金试样高温X射线衍射结果

图5 1号和2号合金试样在不同温度下的X射线衍射图谱

基于Wang等[15]优化的点阵常数模型计算得到1号和2号合金试样的点阵常数随温度的变化，并与高温X射线衍射数据进行比较，如图6所示。由图6可知，试验测定的600～900 ℃范围内γ相点阵常数较Wang等的计算值小，且随温度升高而增大的趋势较缓和，表明相应温度区间内γ相热膨胀系数的试验值较计算值小。该结论与图4中Wang等计算结果及热膨胀仪所测数据比较符合。

图6 试验测定的1号和2号合金试样在不同温度下γ相的点阵常数与Wang等[15]的计算结果

2.2 γ+γ′两相合金

2.2.1 显微组织

图7为经不同工艺时效处理的3号合金试样的显微组织。由图7可见，3种试样均为γ+γ′两相组织，深色区域为γ基体相，浅色区域为γ′相。

图7 经时效处理的合金的显微组织

2.2.2 EPMA相成分

3号合金试样的EPMA图像如图8所示。结合图7可以发现，γ相由更小尺寸(微米级)的γ+γ′两相组成。EPMA测定的3种试样中γ相成分如表5所示。

表5 3号合金的γ相成分(原子分数)

2.2.3 高温X射线衍射分析

图9为3号合金试样在不同温度的X射线衍射图谱，γ′相的特征峰为(210)、(211)。采用Jade软件拟合γ及γ′相的重叠峰(111)、(200)及(220)，选取峰型函数Pearson- VⅡ并参考Tan等[18]的分峰处理方法。由图7和图8的显微组织可知，时效处理后试样中γ′相与γ基体相仍保持较强的共格关系，γ相的弹性模量较γ′相小，受共格应力作用，在分峰拟合时设定γ相衍射峰由γ∥与γ⊥2个亚峰组成并取γ⊥所对应峰位，根据布拉格方程(λCu=1.540 56 Å)计算γ相的点阵常数。图10为3- 1号合金试样的700 ℃X射线图谱中(200)γ,γ′峰的分峰结果， 取αγ⊥作为3号试样中γ相点阵常数。3号合金试样在不同温度的γ相点阵常数及拟合残差如表6所示。

图8 经时效处理的合金的EPMA图像

图9 3号合金试样在不同温度下的X射线衍射图谱

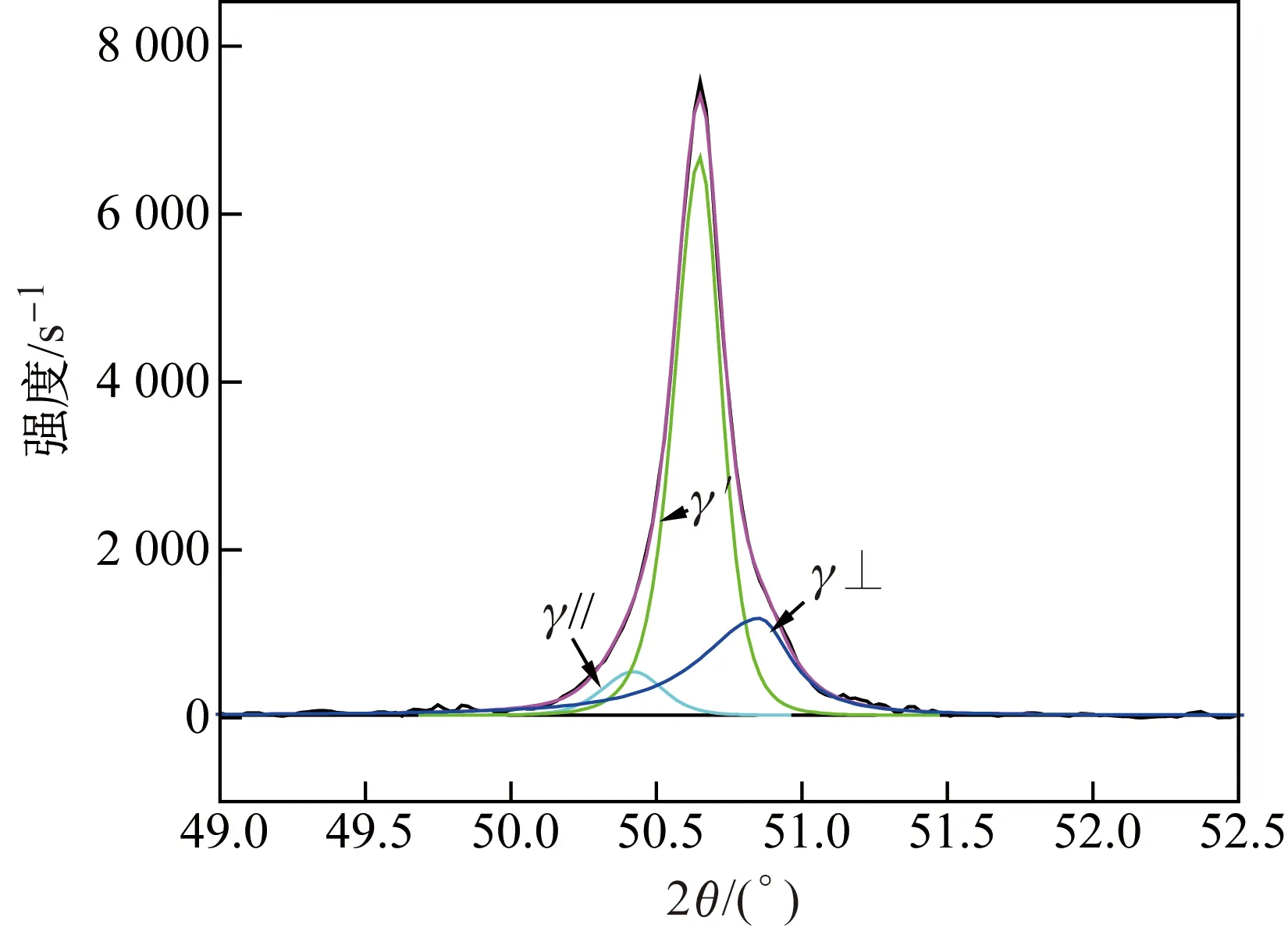
图10 3- 1号合金试样的700 ℃ X射线图谱中(200)γ,γ′峰的拟合结果

表6 3号合金试样X射线衍射结果分析

基于Wang等[15]优化得到的点阵常数模型计算得到3号合金试样中γ相点阵常数随温度的变化曲线，γ相成分采用EPMA测定值。将计算结果与X射线衍射数据进行比较，如图11所示。可得：γ+γ′两相合金在试验温度范围内γ相点阵常数的XRD试验值较Wang等的计算值小，但其随温度的变化趋势与Wang等的计算结果更吻合。

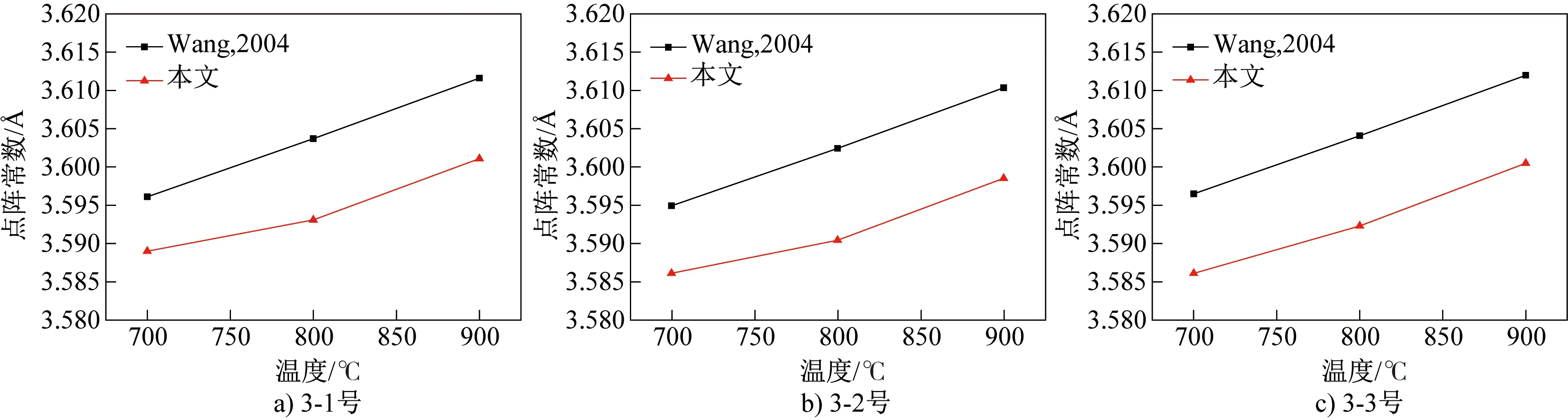
图11 3号合金试样在不同温度的γ相点阵常数的试验值与Wang等[15]的计算结果

如前所述，Wang等在优化γ及γ′相点阵常数模型参数时，仅参考了Kamara等[13]的一组高温试验数据，试样处于γ+γ′两相区。相较于γ单相试样，γ+γ′两相试样中γ相由于受共格应变的作用其点阵常数会发生变化。因此，本文γ+γ′两相合金中,γ相点阵常数的试验值随温度的变化趋势与Wang等的计算结果更吻合。此外，由于参考的高温试验数据有限，本文研究结果表明Wang等的点阵常数模型可能高估了γ相在600～900 ℃范围内的热膨胀系数。

3 结论

(1)试验测定的γ相在600～900 ℃范围内的点阵常数及热膨胀系数均小于Wang等的计算值。

(2)相较于γ单相合金，γ+γ′两相合金中γ相点阵常数的试验值随温度的变化趋势与Wang等的计算结果更吻合。

(3)γ+γ′两相共存时，共格应力会影响γ相点阵常数随温度的变化趋势，而Wang等的点阵常数模型中仅考虑了相成分及温度对点阵常数的影响。