人口迁移行为的时空特征分析

张胜利， 霍 杰,2， 王旭明,2*

(1.宁夏大学 物理与电子电气工程学院，宁夏 银川 750021； 2.宁夏沙漠信息智能感知重点实验室，宁夏 银川 750021)

人类群体行为非常复杂，复杂性源于其决策行为通常是根据个人的知识、经验、意志、判断以及外部环境因素等作出的，且个体间差异巨大.正是这种丰富多彩的个体差异，以及引发社会系统的复杂性吸引了大量的科学家从事人类行为研究.2005年发表在《自然》杂志上的一篇论文[1]，提出了一个基于任务优先级的排队论模型，用时间间隔的幂律分布否定了传统认识即泊松分布.这种统计规律揭示了人类行为发生具有长时间沉默、短时间频发的一种“阵发”特征.2006年，文献[2]借助美元的流通数据,间接揭示了人类空间移动行为所表现出来的既不同于随机游走，又不同于Lévy飞行的独特性质.这两项开创性的研究之后，大量工作相继发表在各大顶级期刊，掀起了有关人类行为动力学研究的热潮[3—7].

迁移行为是人类时空行为研究的重要组成部分.近些年随着研究的深入，提出了许多模型.如类比牛顿万有引力定律提出的空间交互引力模型[8]，从个体对目的地选择的决策过程出发提出了介入机会模型[9]，用排序而不是真实的空间距离来表示目的地距离迁出地的远近，对后续工作产生了积极的推动意义.为了解决前述模型中的待估参数，Simini等[10]提出了辐射模型，假设个体在选择目的地时会选择距离近并且收益高的地方.有研究者认为，个体选择迁入地时不仅要考虑最近且收益最高的区域，而且综合衡量备选空间范围内的所有潜在目的地的收益.为体现这种竞争效应，文献[11]提出了人口权重机会模型，即迁出者选择目的地的概率正比于目标城市的人口规模，反比于迁出区与迁入区两地之间的人口总数.整体来看，这些模型本质上都是静态模型，适用于研究长时间尺度的空间交互行为.在研究出行者交通行为[12]、疾病时空传播过程[13]、网络通信设计[14]等需要及时反馈信息的问题时，其略有不足.与此同时，Song等[15]利用手机数据对人类空间移动模式进行统计分析时，发现了有无法用连续时间随机游走模型解释的标度异常现象，进而建立了一个探索和偏好返回模型.由于人类空间移动具有强烈的记忆性[16]，基于这些考虑，文献[17]建立了有限空间中的记忆性偏好随机游走模型.前已述及，都未将个体和群体移动模式预测归为统一模型.闫小勇等[18]设计了一种能够同时预测个体和群体空间移动的统一模型，这对于详细刻画个体群体移动模式具有较高的研究价值.然而此模型过多侧重于研究城市内局部空间的人口移动行为，对于长程迁移却未充分考虑.因此，在兼顾个体与群体的同时，揭示不同空间级别迁移行为所具有的规律，成为新的研究方向.

基于互联网技术的大数据分析，使得宏观层面研究人类时空行为成为可能.定量分析人类行为与社会发展正成为跨学科研究的热点.笔者通过数据挖掘，获得美国近些年170个城市人口规模与区域经济发展指标(国内生产总值，GDP)的统计数据，在分析实证统计规律的基础上建立了以追求高经济利益为驱动力，以迁入区与迁出区几何距离表征的心理排斥力的合力作用下的人口迁移动力学模型，模拟区域间人口迁移行为，再现实证规律，预测未来人口分布以及区域经济发展趋势，并深入理解规律产生的内在机制.

1 区域人口与GDP的实证统计

本文对美国170个城市2012—2017年人口规模(L)和国内生产总值(GDP)的数据[19—20]进行统计分析，对应人口规模概率分布满足图1a所示的类高斯关系

(1)

式中：a1=65 174.38±2 195.79，w1=48 541.40±4 512.69，b1=10 479.40±887.54.对于同时间段的能够表征区域经济发展程度的GDP分布，通过比较P(Y,t)∝a2Yb3的拟合误差，(a2=215.72±114.38，b3=-0.88±0.06)，与图1b所示的

图1 美国170个城市人口、GDP分布规律

P(Y,t)∝b2e-Y/c1

(2)

的拟合误差(b2=0.26±0.01，c1=9 821.03±692.80)，发现后者更合理.将该统计结果与同时期的中国人口规模和经济发展水平分布相比较[21]，可看出两国间存在巨大差异.究其原因，必然是人口迁移行为特点的差异引发区域间人口分布以及经济发展程度的不同.在中国，经济因素是影响人口迁移的主要因素，人口的区域分布和经济规模分布均服从漂移幂律[22].在美国，以环境和文化为代表的非经济因素与经济因素影响相当[23].可能是这两种因素交互作用导致美国人口和区域经济发展程度分布不同步，且相互关联性减弱.因而，研究美国人口和区域经济分布的新特征形成机制就显得尤为重要了.

2 人口迁移动力学模型

如图2a所示，对于迁出地居民而言，任意一个经济发展程度比其高的区域都有可能被选为潜在目标迁入地(一对多)；如图2b,对于迁入地，多个地方的居民可以选择迁入同一地(多对一).模型的动力学方程可以描述为

图2 人口迁移规则

(3)

区域经济变化采用经典的柯布-道格拉斯(C-D)生产函数予以表征，即

Y=A(t)LαFβ，

(4)

式中：Y为GDP，反映区域的经济发展程度；A(t)为生产过程中的综合技术水平，是一个随时间变化的参量；L为劳动力数量，这里简化看作区域人口规模；F为固定资本投资；α和β分别为区域人口规模和固定资本投资的弹性系数，3个变量随时间的更新法则是

(5)

式中:γ和η分别为ΔL和ΔF对A的影响权重因子；Knat为区域i在t时刻的净出生率(出生率减去死亡率)；Lout(i,t)为区域i在t时刻的迁出人数;Lin(i,t)为区域i在t时刻的迁入数.从上式可以看出，生产函数中的几个量在更新时，不仅与自身变化有关，同时也考虑了互相间的反馈调节.

3 模型检验

为了检验模型的合理性，建立了30×30满足周期性边界条件的网格，每个节点代表一个区域i，每一个区域上分布有若干居民.模型初始时刻，区域人口规模0≤L≤120，综合技术水平0≤A≤2 000，固定资本投资0≤F≤200，为随机均匀分布.依据C-D生产函数,区域的GDP在初始时刻非线性依赖于区域人口规模L、综合技术水平A和固定资本投资F.其他参数α=0.8,β=0.3,γ=0.25,η=0.15,净出生率Knat=0.001，迁出率Kout=0.25,当量D=20时，为了将模拟结果与实证统计结果进行比较，选取不同时刻的区域人口规模、GDP进行统计分析(图3).由于人口迁移是多种因素共同决定的复杂行为，造成模拟结果与实证统计结果无法精确比对.图3b，3c和图4概率分布与实证统计结果趋势一致，特别是模拟一段时间后(t=5 500)，区域人口规模满足高斯分布

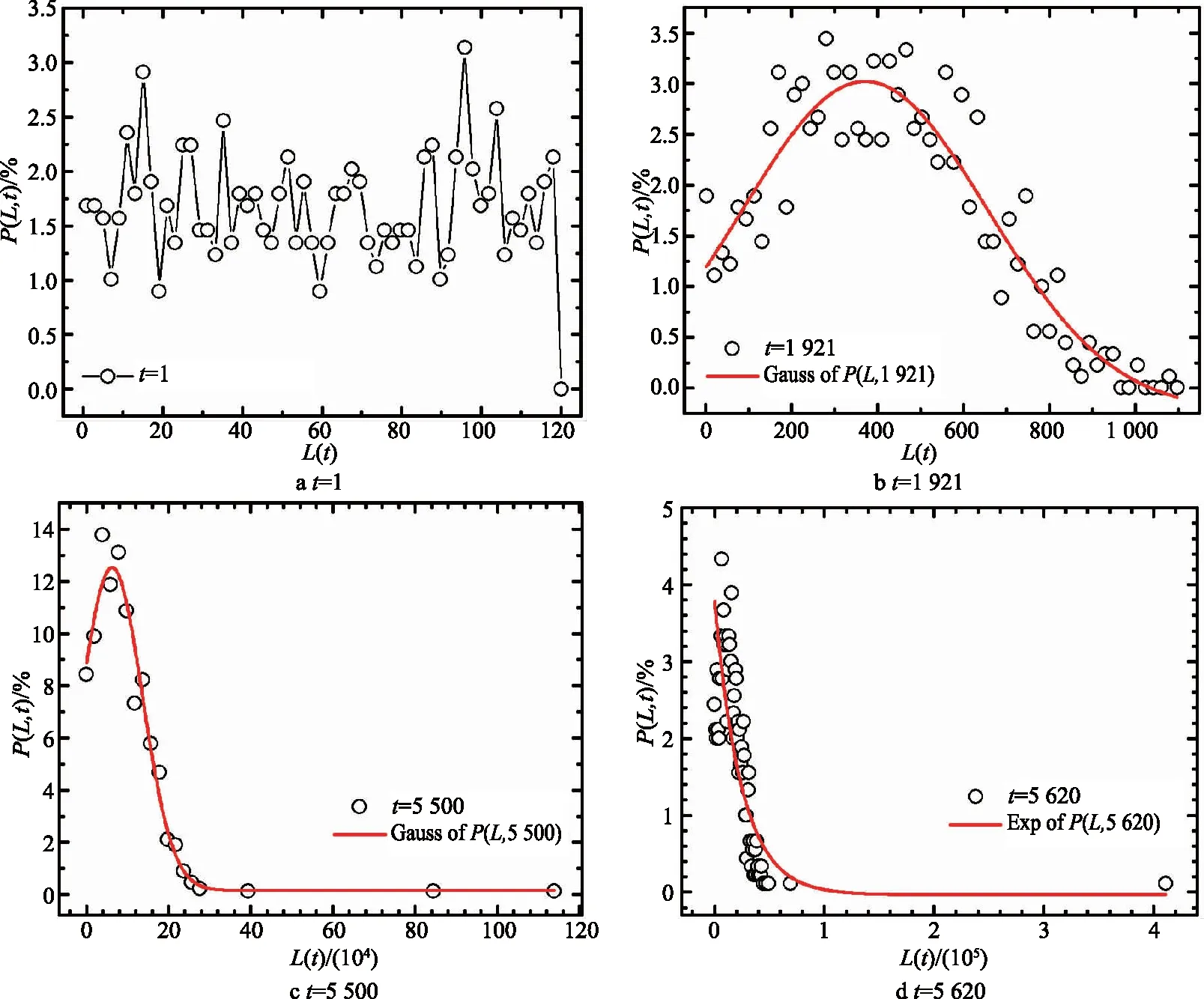
图3 区域人口概率分布情形

图4 区域GDP分布情形

(6)

式中：a3=9 337.60±641.27,w2=22 063.43±1 678.79,b4=342 404.72±29 693.60，而区域经济规模GDP初始时刻满足指数分布P(Y,t)∝b5e-Y/c2,b5=6.53±0.29,c2=81 577.34±8 532.68，经长时间模拟后其分布趋势并未发生改变，只是参数略有不同(t=5 000,b5=14.81±0.44,c2=124 668.10±8 631.39).比较结果说明，此种规则下的模型可以较好地再现美国这类经济较发达国家的人口迁移行为.随着模拟的进行，区域人口分布出现对高斯分布的偏离，逐步转变为指数分布形式.这种变化过程意味着，在人口迁移行为作用下，社会由初始的无序的随机分布逐步转变为相对有序分布.无序状态可以用类高斯分布表示，而由类高斯演变为指数分布标志着比较有序社会的建立.

4 理论结果分析

4.1 人口结构信息熵[25]

不确定性是人口迁移行为的本质属性，而“熵”是描绘随机过程演化方向的重要工具.本文引入信息熵来描述人口群体迁移所引发的系统无序性的变化过程.众所周知，“熵”最早出现于物理学领域，用于描述系统非平衡过程，后逐渐拓展到化学、生物、天文以及信息科学等领域，并成为复杂系统演化中有序、无序的重要判据.现实社会，人口迁移必然会引发区域人口在不同时步或大或小的变化，导致人口分布的改变，进而推动社会系统向某一方向演化.具体影响怎样？本文定义t时步各区域人口数占系统总人口数的比例为

P(i,j,t)=L(i,j,t)/L0,

(7)

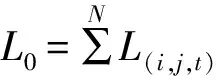
(8)

根据信息熵的定义，可得出人口迁移所引发的人口结构信息熵随时间的变化过程，见图5.整体来看，熵值先快速增大，随后缓慢持续减小，对应拐点出现在t=1 921时步.这说明，最初迁移时人们对外界的信息量掌握相对较少，迁移的目标性不强，迁移行为存在盲目与混乱，导致系统人口结构变得无序，熵值增大；随着时间的推移，通过各种渠道，人们掌握的信息量逐渐增多，迁移逐步变得理性起来，迁移行为是在综合了各种因素之后的理性决定，目的性增强，行为也越加有序.与之对应地，人口结构变化也由无序向有序转变，熵值由增变减.为了进一步揭示这一变化过程的内在机制，本文将借助人口迁移动态网络结构来研究此种背景下的人口迁移行为特征.

图5 人口结构信息熵随时间的变化趋势

4.2 人口迁移网络结构特征研究

人口迁移网络与其他网络结构一样，都是由节点和节点间连边所组成的.本文模型在模拟时构建一个30×30的网格，将发生人口流动的格点定义为节点，若两节点间发生人口迁移，则存在网络连边，在这些基本元素的基础上构成了人口迁移有向动态网络.在原有参数维持不变的前提下，选取3个时步(t=1，1 921，5 620，见图6)，来细致描绘人口迁移空间结构特点，分析人口分布规律随时间的推移的变化.

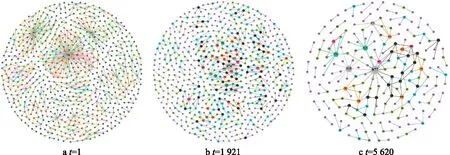
图6 人口迁移网络结构图

从人口迁移网络结构图(图6)可以看出，迁移初期，呈现大规模的迁移现象，近乎形成全连通网络.由于人口流动涉及区域较多，造成人口分布的对称性较低；随着时间的推移，迁移规模逐渐减小，人口迁移的指向性凸显，中心区域形成.在这个变化过程中，图6b为熵值较大时刻所呈现的人口迁移网络结构图，从图中可看出，此时整个网络的连接度较低，且较大连接度的节点较多，人口迁移方向的可选性减少，系统混乱度增高.但当中心区域逐步形成，系统的混乱度也随之降低.如图6c所示，标号877的区域成为人口流入的主要目的地，整个系统的人口分布结构趋于有序，信息熵逐步降低.这一模拟结果与美国的实际迁移特点相一致[24].

为了进一步研究人口迁移行为网络结构特点，本文对上述3个时刻的网络的度分布进行了统计分析.结果表明，其度分布满足幂律关系

P(k,t)∝ka3，

(9)

式中:a3(1)=-1.841±0.549,a3(1 921)=-1.851±0.672,a3(5 620)=-2.138±0.706.拟合结果表明，人口迁移网络满足无标度网络结构特点，其度分布满足幂律关系.这同时印证了人类社会系统中“巨集团”的存在，以及人口迁移稳定流向的“脆弱性”.

图7 人口迁移网络度分布规律

5 结果与讨论

本文在分析美国区域人口和国内生产总值数据的基础上，提出了以区域间人均GDP之差为驱动力、以区域间欧氏距离表征心理排斥为阻碍力的人口迁移行为动力学模型.模型的核心思想是区域间的人口流动主要是基于经济利益驱动下的人口迁移行为造成的.同时，迁出区与迁入区两点间的自然环境、社会资源以及空间距离等因素都会给居民的迁移决策产生很大的影响，可将这些因素一并看成是影响迁移行为的心理斥力.由此构建出了体现动力与阻力的动力学模型来模拟人口迁移行为.

为了检验模型的合理性，将模拟结果与实证结果进行对比.结果表明，区域人口规模和经济发展程度的模拟结果与实证统计结果趋势一致.从整体模拟结果上看，区域人口规模的分布由初始的随机均匀分布逐渐演变到类高斯分布，经高斯分布后，最后过渡到指数分布；区域经济发展程度的分布则始终满足指数关系.从过程来看，演化初期，人口是随机分布在整个区域中的，GDP的初始值非线性的依赖于人口规模、综合技术水平和固定资本投资，依据C-D生产函数给出.经济的不均衡引发人口流动，这种行为不仅改变了区域的人口分布，同时反馈于区域经济发展，使其分布发生细微的调整.对于这两种截然不同的变化过程，可以从不同的两个视角予以理解.人口分布的变化是驱动力与阻碍力、确定性与随机性博弈的结果.而区域经济发展程度分布的相对稳定可以理解为决定因素的更替.社会发展初期，因各区域人口规模较小，区域间综合技术水平、固定资本投入的差异决定经济发展程度的分布规律.而随着人口规模的自然增长和区域间的流动，人口分布形式必然会成为影响经济发展程度分布的主导因素，并将持续作用.

通过对人口迁移行为的时空分布特征的研究表明，社会系统趋于有序，与人口信息熵相互印证；借助人口迁移动态网络可以较好地帮助人们理解不同时期人口迁移特点；迁移网络度分布规律说明人口迁移方向的不确定性以及社会中“巨集团”的存在.通过本文的研究可得，人类时空行为规律是由影响人口迁移行为的确定因素和随机因素共同作用的结果，规律的差异只是由于这两种因素“合力”方向不同而已.此外，复杂网络的研究方法不仅可以更为直观地展现研究细节，同时也可以揭示规律形成的内在机制，丰富了社会系统的研究手段.