关于Enabling理想

雷 震

(安徽师范大学 数学与统计学院,安徽 芜湖 241000)

Alkan等人在文献[1]中引入了环的enabling理想,是Nicholson等人在文献[2]中提出的强提升理想(strong lifting ideal) 的推广.环R的一个理想I称为强提升的,是指对于任意a∈R,满足a-a2∈I,存在一个幂等元f(f=f2)∈aR(或者f∈Ra,或者f∈aRa),使得a-f∈I.强提升理想及enabling理想都是基于幂等元提升而推广的,其目的在于利用环的同态研究环的相关性质,特别作用在clean 环、exchang环及相关环上(参见文献[1-4]).文献[2]针对enabling理想提出了3个公开问题,文献[5]回答了第二个公开问题:若环R的理想I是enabling理想,则R上一元多项式环R[x]的理想I[x]不必是R[x]的enabling理想,文献[6]解决了第三个公开问题:若环R的理想I是enabling理想,则R上幂级数环R[[x]]的理想I[[x]]是R[[x]]的enabling理想,但第一个公开问题至今未能解决,即如果I是环R的enabling理想,那么环R上的n阶矩阵环Mn(R)的理想Mn(I)是否为enabling.在研究第一个公开问题的过程中.受上述文献研究结果的启发,我们获得了相关结论,改进了若干已知结果.本文所有的环均指有单位元的结合环(除非特殊说明).

定理1若环R上的矩阵环Mn(R)的理想Mn(I)是enabling理想,则I是R的enabling理想.

证明设a-e∈I,这里a,e(e=e2)∈R.下证存在R的一个元r,使得ar为幂等元,且a-ar∈I.由于a-e∈I,从而

为Mn(R)的幂等元,且

所以a-ar11∈I,注意到ar11=(ar11)2∈aR,因此I为R的一个enabling理想.

根据定理1的证明,容易得到下列命题.

命题1若环R上的矩阵环Mn(R)的理想Mn(I)是强提升理想,则I是R的强提升理想.

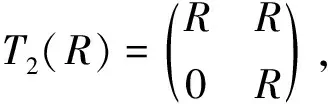
定理2设I是环R的一个理想,则下列条件等价:

(ⅰ)I是环R的enabling理想;

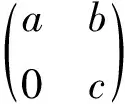
容易验证

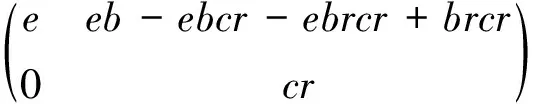
为环T2(R)的幂等元.

下证e-(eb-ebcr-ebrcr+brcr)∈I.用x≡y表示x-y∈I,根据上述证明可知c-f∈I,b-d∈I,c-cr∈I及d=ed+df,所以b≡d,c≡f≡cr,edf=0,进而有b≡eb+bf≡eb+bc及ebc≡0,所以

b-(eb-ebcr-ebrcr+brcr)=

b-eb+ebcr+ebrcr-brcr=

-eb+ebcr+ebrcr+b(1-rcr)≡

-eb+ebcr+ebrcr+(eb+bc)(1-rcr)=

-eb+ebcr+ebrcr+eb(1-rcr)+bc(1-rcr)≡

ebcr+b(c-crcr)≡ebc≡0.

因此e-(eb-ebcr-ebrcr+brcr)∈I,即

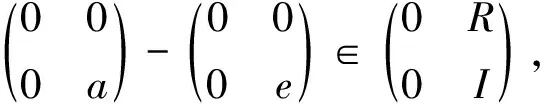
环R对于其自身来说显然是其一个enabling理想,根据定理2立即可得下列推论.

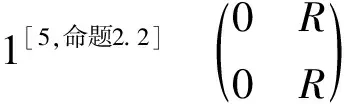
类似于定理2的证明,可以得到如下命题.

命题2设I是环R的一个理想,则下列条件等价

(ⅰ)I是环R的强提升理想;

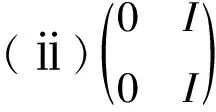
有单位元1的环R的一个理想I称为弱enabling理想(weakly enabling ideal),是指对于任意a∈R,满足a-1∈I,存在一个幂等元f(f=f2)∈aR(或者f∈Ra,或者f∈aRa)使得a-f∈I(参见文献[2]).类似定理2的证明，同样可以得到如下命题.

命题3设I是有单位元的环R的一个理想,则下列条件等价：

(ⅰ)I是环R的弱enabling理想;