异径四通的塑性极限分析
张 鹏,惠 虎,黄 淞
(华东理工大学 机械与动力工程学院,上海 200237)
0 引言
异径四通具有既能改变介质流动方向;又可以改变介质流速的优势,是工程中常见的管件之一,广泛应用于水利、石化等领域。就其结构而言,异径四通的几何结构较为复杂,在正常的工作条件下,其相贯线位置存在应力集中现象[1],该处为异径四通管件的薄弱位置,一旦发生失效现象,就会直接影响相应系统的正常运行。然而,长期以来针对异径四通问题的研究相对较少,因此对异径四通极限载荷的研究是很有必要的。
目前大批学者针对直管、弯管、三通和四通等管道连接件的塑性极限载荷进行了研究,近年来,对弯管、三通的相关研究成果很多。郭茶秀等[2]系统地分析联合载荷下周向面型直管的塑性极限载荷,建立了内压、弯矩、扭矩联合作用下的塑性极限载荷方程。王辰等[3]针对内压下含纵向裂纹弯头的塑性极限压力进行研究,建立了含缺陷弯头塑性极限载荷工程估算式。轩福贞等[4-5]对无缺陷及含缺陷的焊制三通开展了一系列的研究,得到了不同载荷下三通的失效形式及相应的塑性极限载荷工程估算式。但是,关于四通管件塑性极限载荷的研究相对匮乏,很少有理论成果可做参考,而在压力管道系统特别是油气开采及输送管道中,四通管件的使用较多[6]。刘张羽等[7]通过大量有限元算例,建立了四通塑性极限内压的数据库,拟合得到了形式简单、精度较高的无圆角四通塑性极限内压拟合公式。
采用ANSYS Workbench仿真软件对异径四通进行数值分析,通过改变支管管径、壁厚及过渡圆角等尺寸参量计算四通塑性极限内压,在此基础上研究四通应力分布及四通失效特征及拟合出塑性极限内压工程估算式,并通过模拟试验对拟合公式进行验证,为后续含缺陷四通塑性极限内压研究提供参考。
1 四通有限元模拟
1.1 模型建立与网格划分
四通管件的成型工艺通常采用液压胀形[8]及热压成形[9],在成型过程中四通各部位的壁厚不等,且ANSI/ASME B31.3—2014标准中未给出四通管件过渡圆角曲率半径确定值。本文在实际四通尺寸参数基础上,对模型进行适当简化。四通管件采用等圆角过渡方式,主要尺寸见简化后的几何模型(见图1),将四通管件简化为两个圆柱体相贯,根据结构及载荷的对称性,有限元模型仅建立实体结构的1/8,其中主管外径 238 mm,主管长度420 mm,支管长度 530 mm。材料为ZG30CrMo,材料选取理想弹塑性弹性模型,弹性模量E=2.05×105MPa,屈服强度σs=475 MPa,泊松比μ=0.3。
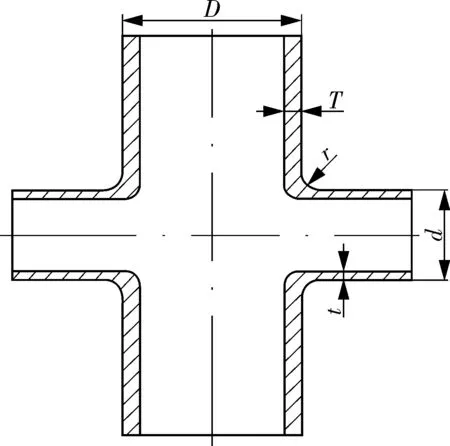
图1 四通管件几何模型示意Fig.1 Schematic diagram of geometrical model ofreducing cross
采用实体单元对模型进行网格划分。为更好地反映应力的分布规律,需要对应力集中区域网格进行网格加密处理,在此基础上,进行网格无关性验证,选择合理的网格划分方式。典型的无缺陷异径四通网格划分见图2。
1.2 载荷及约束条件
在本文研究过程中采用1/8模型,在管件内表面施加均布内压P,对称面施加无摩擦对称约束,主支管端部施加轴向拉伸载荷F以模拟端部封闭的情况[10],轴向拉伸载荷F:
(1)
式中,F为管端面等效均布拉伸载荷,MPa;P为管道内压,MPa;Di,Do为管道内径及外径,mm。
1.3 极限载荷的确定方法
极限载荷是指构件在外载荷作用下、整体或某一局部的全厚度上,由弹性状态而进入塑性状态时所对应的载荷。构件理想极限状态时,承受的载荷不变而变形量无限增加,但实际上材料并非理想弹塑性且仅发生小变形,工程中认为结构发生显著的整体塑性变形时所对应的载荷即为塑性极限载荷。
有限元分析过程中,通过载荷增加法使结构逐渐进入屈服、达到显著塑性变形状态[11-12]。在有限元计算过程中,当载荷大于结构的塑性极限载荷,将会导致程序发散及求解失败,通常将有限元计算至发散时对应的载荷作为结构的极限载荷。本文采用ANSYS软件,为了得到良好的收敛解,计算过程采用小变形假设。
2 极限载荷计算结果及分析
四通管件主要尺寸如图1所示,本文以主管外径238 mm的四通为主体,分别以A=d/D,B=t/T,C=D/T,D=r/D为参数对异径四通管件的极限内压PL1进行研究。为便于对比分析,使得极限内压不依赖于具体的尺寸参数,对极限内压PL1无量纲化处理,定义四通管件无量纲极限内压PL为极限内压PL1与相同几何结构直管的极限内压P0的比值。
PL=PL1/P0
(2)
其中,据塑性失效设计准则[13]可知:
(3)
本文通过对GB/T 12459—2017《钢制对焊管件类型与参数》及API SPEC 6A—2010规范中关于四通尺寸参数的统计分析、结合工程需求,选取本文研究中四通各尺寸参量范围如表1所示。
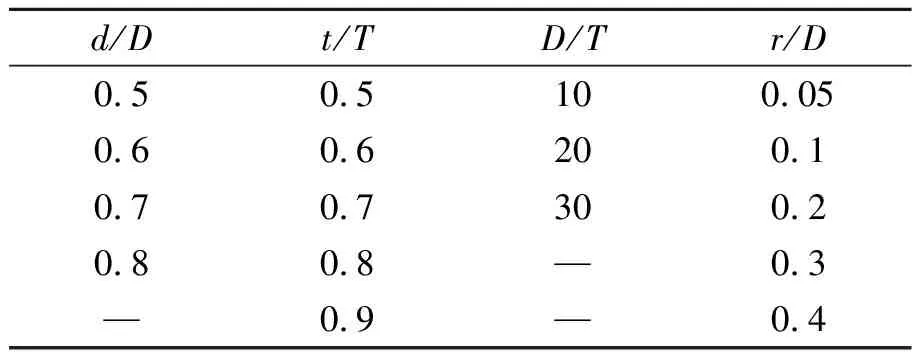
表1 四通各尺寸参量范围Tab.1 Dimension parameter range of reducing cross
通常需要对不同四通的尺寸参量进行组合,来研究不同参数对试验结果的影响,但本试验因素较多,全部实施较为耗时。正交试验设计主要针对多因素多水平,根据正交性,从全面试验中挑选出部分有代表性的点进行试验,这些点具备了均匀分散及可比的特点,故本文采用设计正交试验的方式对几何参量进行分析。
2.1 异径四通失效特征分析
2.1.1 异径四通不同部位应力分布随内压升高的变化
异径四通管件属于典型的不连续结构,在主支管相贯线处应力集中现象明显。相贯线及附近区域是整体异径四通管件最危险的位置,因而,沿相贯线的应力需要重点关注。按图3所示提取相贯线处应力分布,通过对比不同载荷下异径四通应力分布情况,得出四通塑性区的发展趋势。
不同载荷下异径四通的应力分布云图如图4所示,异径四通最大应力点首先出现在内壁肩部及外壁腹部,并随着载荷的增加逐渐沿相贯线及壁厚方向扩张。
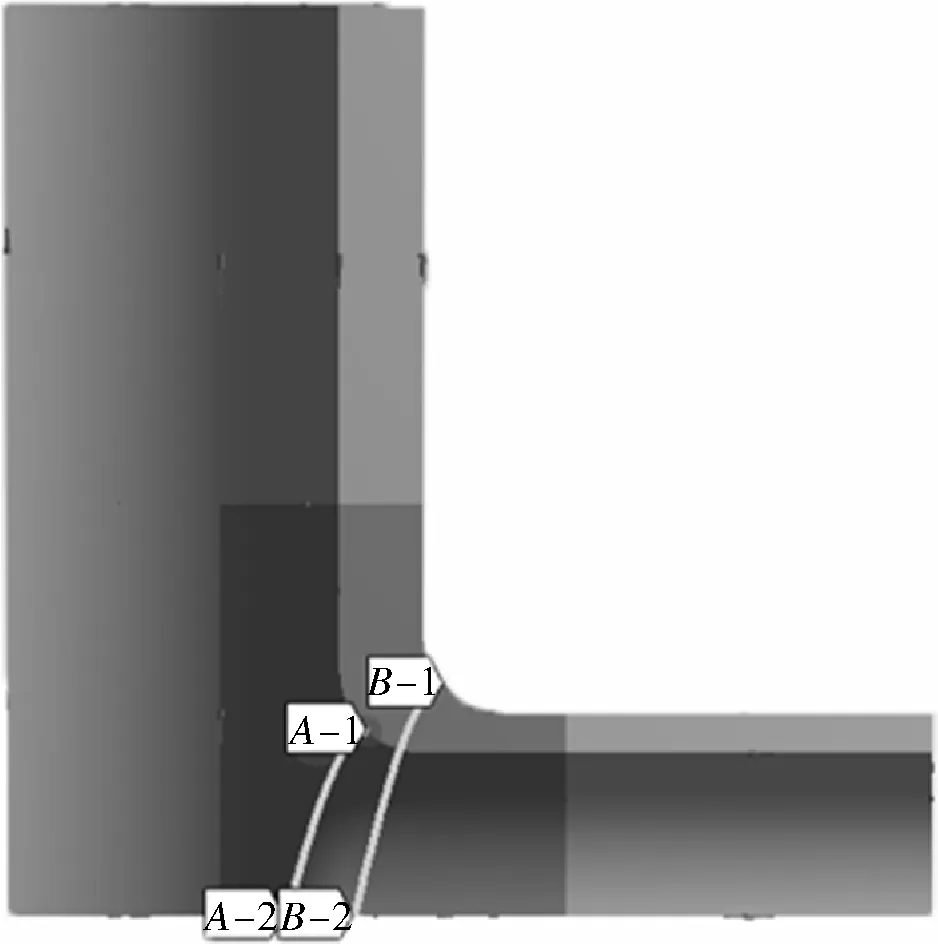
(a)相贯线处应力取值位置
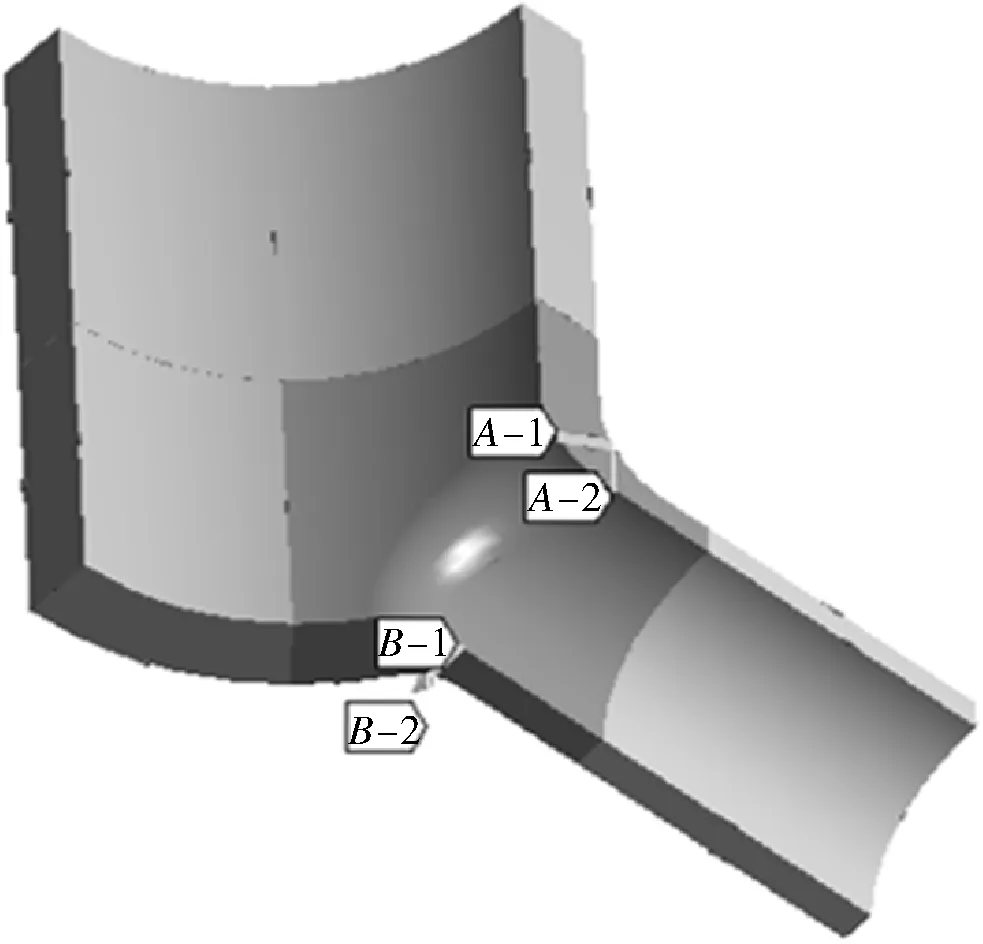
(b)肩部、腹部壁厚处应力取值位置图3 应力取值位置示意Fig.3 Schematic diagram of stress value location
图5示出不同载荷情况下,异径四通管件沿内壁及外壁相贯线处的Mises当量应力分布,其中横坐标代表沿相贯线肩部至腹部的不同位置,纵坐标代表当量应力与屈服强度的比值。可以看出,在弹性范围内,四通内壁最大应力点出现在肩部;而四通外壁最大应力点出现在腹部;随着压力的升高,在内壁肩部先于外壁腹部达到屈服,在内壁塑性区由肩部逐渐向腹部发展,在外壁塑性区由腹部向肩部发展;随着压力继续不断升高,塑性区不断扩大,直至整个四通管件相贯线区域全部进入塑性区,认定此时四通管件失去承载能力,达到极限状态。

(a)异径四通内壁

(b)异径四通外壁图4 不同载荷下异径四通的应力分布云图Fig.4 Stress distribution nephogram of reducing cross under different loads
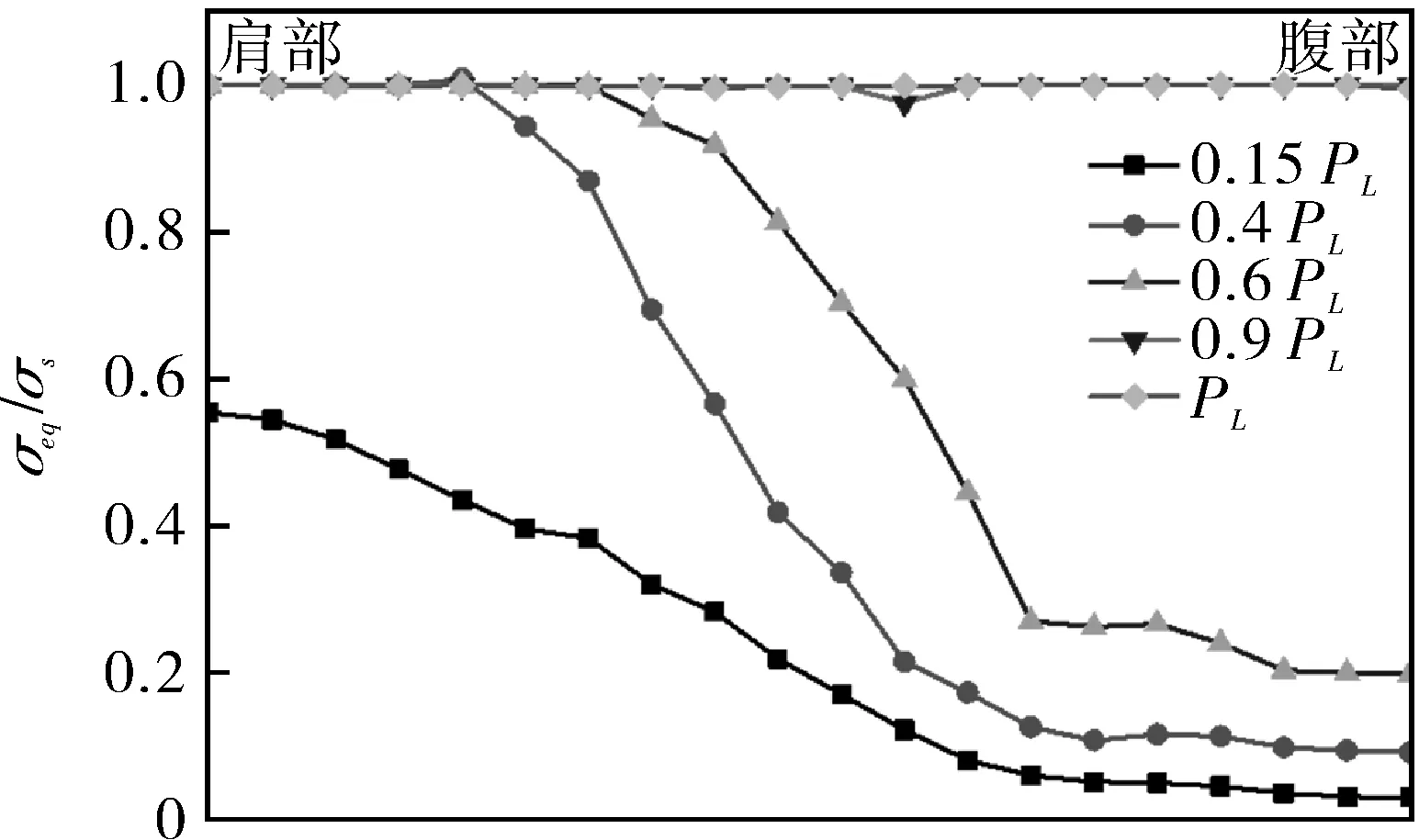
(a)异径四通相贯线内壁当量应力分布
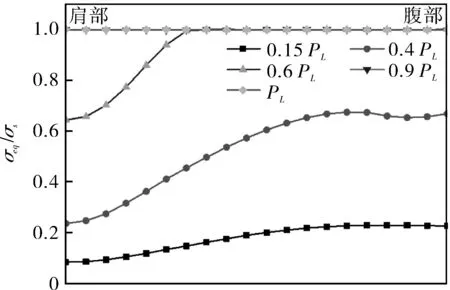
(b)异径四通相贯线外壁当量应力分布图5 异径四通相贯线当量应力分布Fig.5 Equivalent stress distribution of intersectionline of reducing cross
图6示出不同载荷情况下,异径四通管件沿内壁及外壁沿壁厚方向的Mises当量应力分布,其中横坐标代表沿壁厚由内壁至外壁的不同位置,纵坐标代表当量应力与屈服强度的比值。可以看出,四通肩部最大应力点出现在内壁,随着压力的升高,内壁肩部逐渐屈服,塑性区由内壁向外壁扩张,继而沿壁厚方向整体进入塑性区;四通腹部最大应力点出现在外壁,随着压力的升高外壁腹部逐渐屈服,塑性区由内壁向外壁扩张;与肩部相比,腹部内外壁之间存在低应力区。
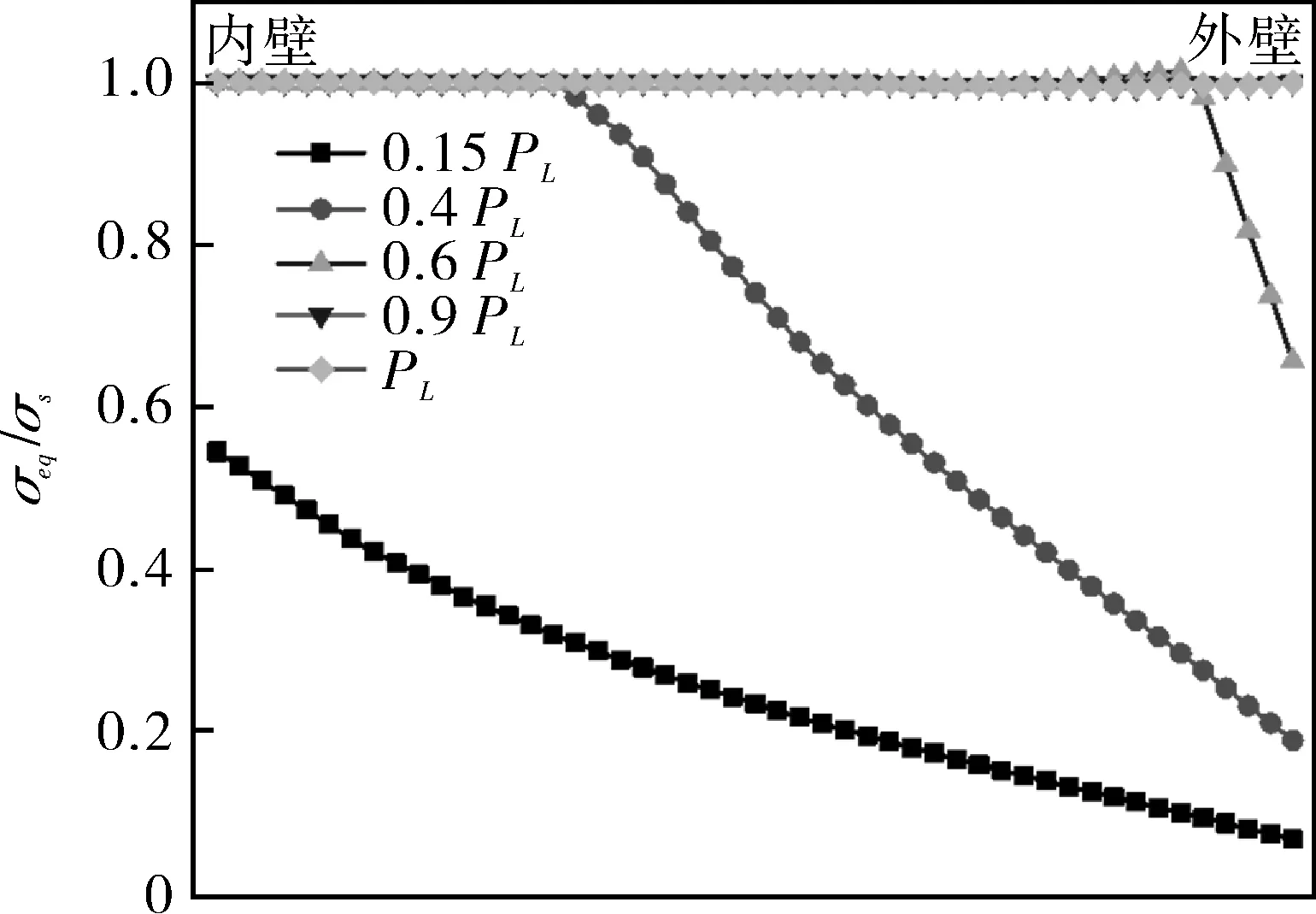
(a)异径四通肩部当量应力分布
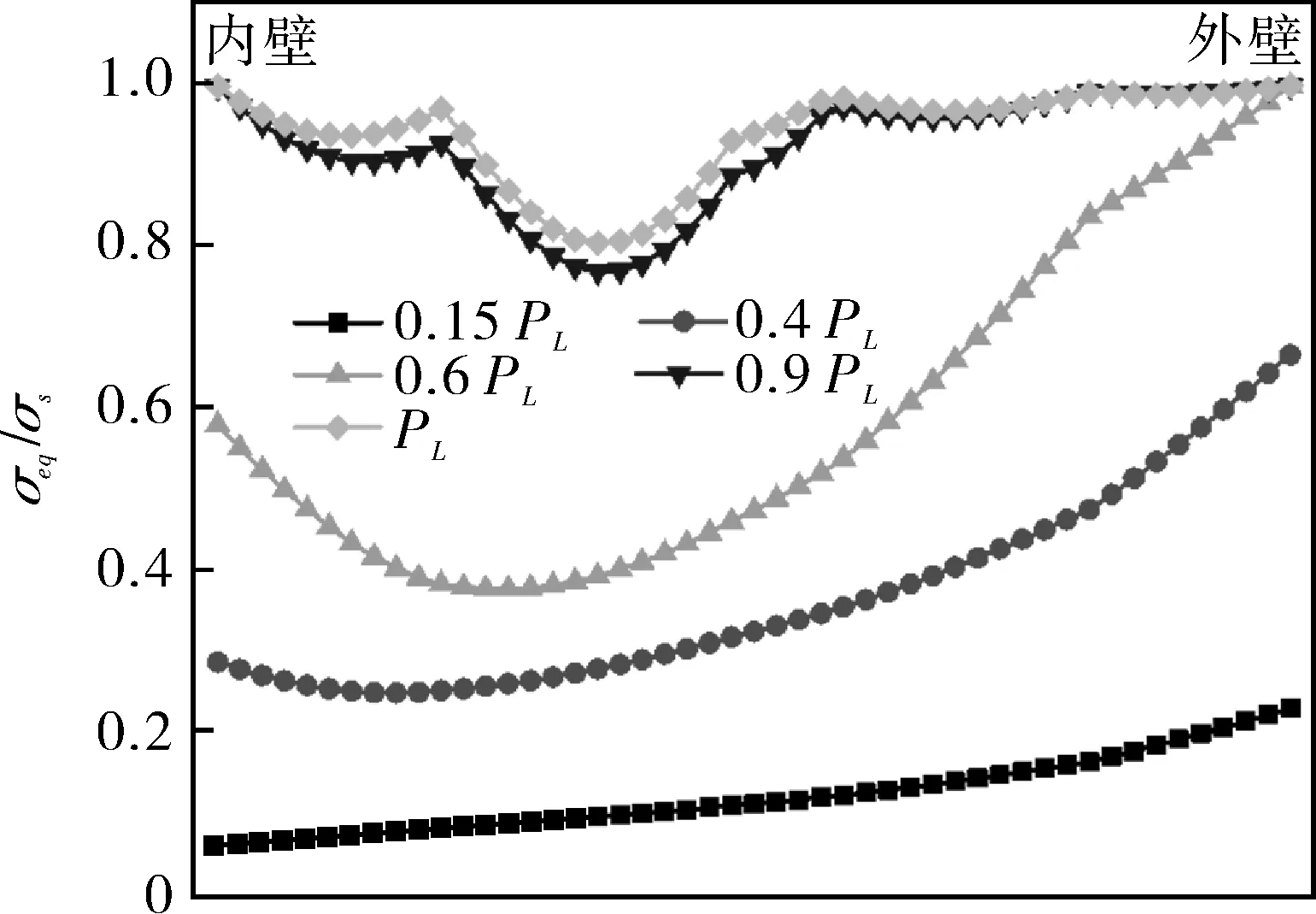
(b)异径四通腹部当量应力分布图6 异径四通肩部及腹部当量应力分布Fig.6 Distribution of equivalent stress in shoulderand abdomen of reducing cross
2.1.2 异径四通极限状态下的变形特征
图7示出异径四通模型极限状态下的变形情况,可以看出在极限状态下四通的变形特征:肩部发生较为明显的内塌变形,支管有一定的径向收缩现象;四通腹部区域发生了明显的鼓胀,最大变形区出现在腹部相贯线附件的位置,据此可得导致四通在内压作用下破坏的主要原因是相贯区附近变形量过大。

图7 异径四通模型极限状态变形情况Fig.7 Limit state deformation of reducing cross model
2.2 尺寸参数对极限内压PL的影响分析
结合失效特征分析及表1中几何参量,本文选取主管外直径为238 mm,改变其他尺寸参量进行试验,为减少工作量,采用混合正交试验SPSS软件确定正交表,在其基础上进行模拟,得出试验结果如表2所示。
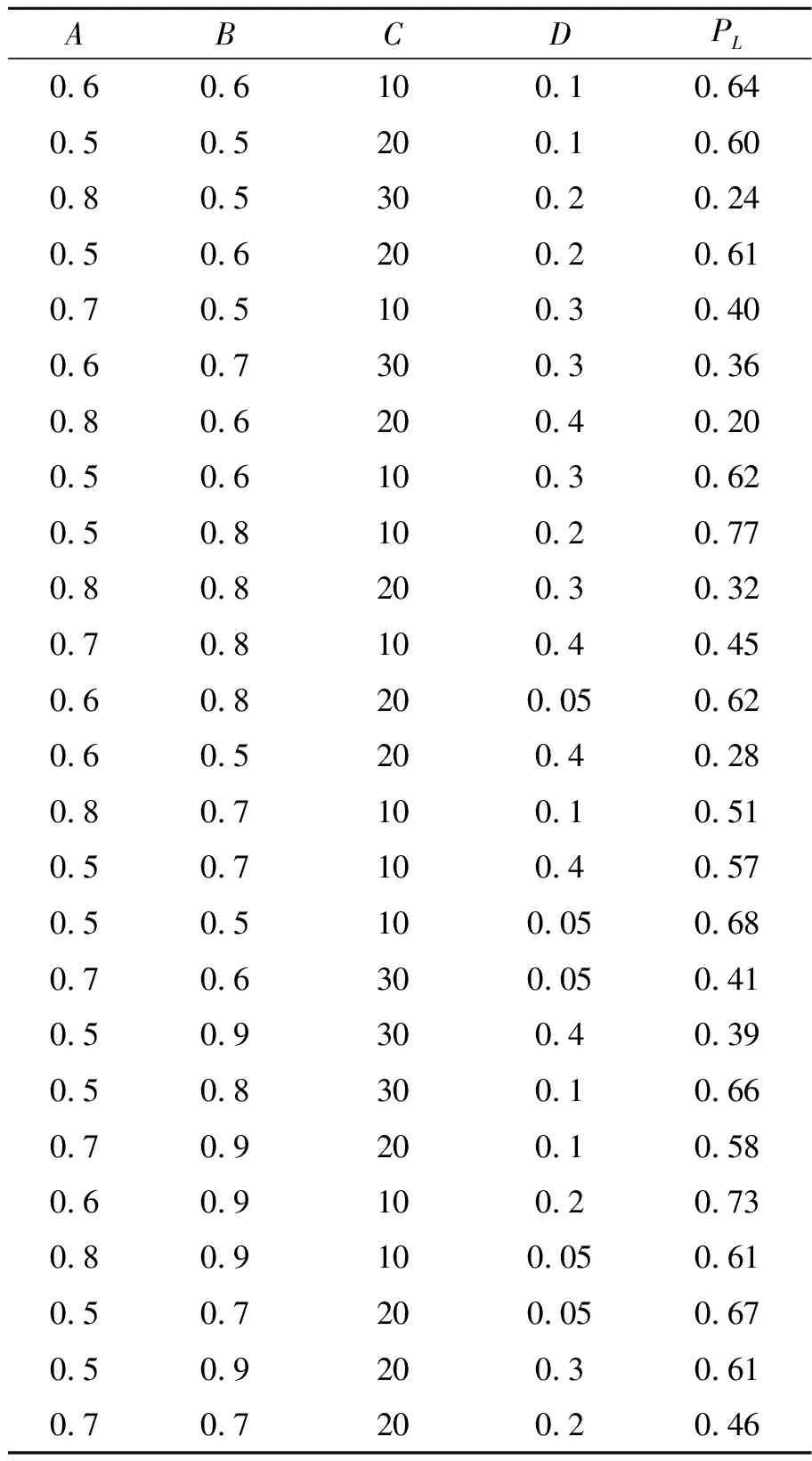
表2 极限内压PL正交试验结果Tab.2 Experimental results of PL orthogonalityin limiting internal pressure
在研究单个尺寸参数对无量纲极限内压PL的影响时,分别考虑单个变量的边际均值(剔除其他变量影响时算出的均值),如表3所示。
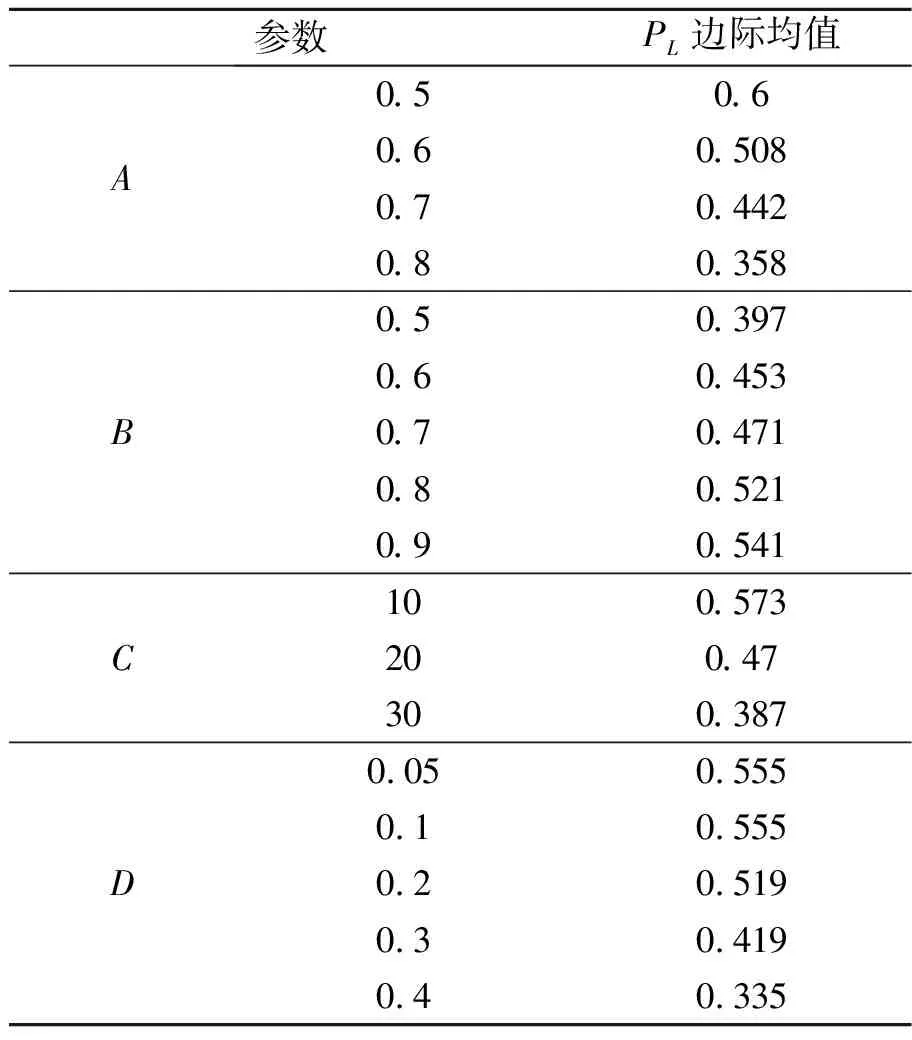
表3 几何参数及对应极限内压PL的边际均值Tab.3 Geometric parameters and their marginal meanvalues corresponding to the limit internal pressure PL
利用Origin对算例的有限元解进行曲线拟合。拟合结果如图8(a)~(d)所示,分别反映了A,B,C,D四个尺寸参量对四通无量纲极限内压PL的影响。通过图8(a)可以看出,随着支主管径A的逐渐增大,极限内压PL逐渐减小;由图8(b)可以看出,随着支主管径壁厚比B的逐渐增大,极限内压PL逐渐增大;由图8(c)可以看出,随着主管径厚比C的逐渐增大,极限内压PL逐渐减小;由图8(d)可以看出,随着过渡圆角与主管径比D的逐渐增大,极限内压PL逐渐减小;A,B,C近似于线性分布,D近似于二次分布。
2.3 异径四通极限载荷工程估算式拟合及验证
对试验结果进行多元回归分析,4个几何参数的对极限载荷PL具有显著影响,通过对比标准化系数可得:参数A=d/D,B=t/T,D=r/D对极限载荷PL为负向影响,C=D/T对极限载荷PL为正向影响,影响最大几何参数为主支管壁厚比,建立本文研究范围内几何参数变化可适用的工程估算式为:
PL=1.02143-0.79941A+0.356B
-0.00944C-1.56638D2+0.0445D
(4)
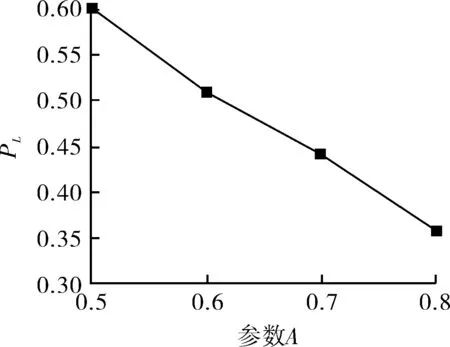
(a)尺寸参量A对PL的影响 (b)尺寸参量B对PL的影响
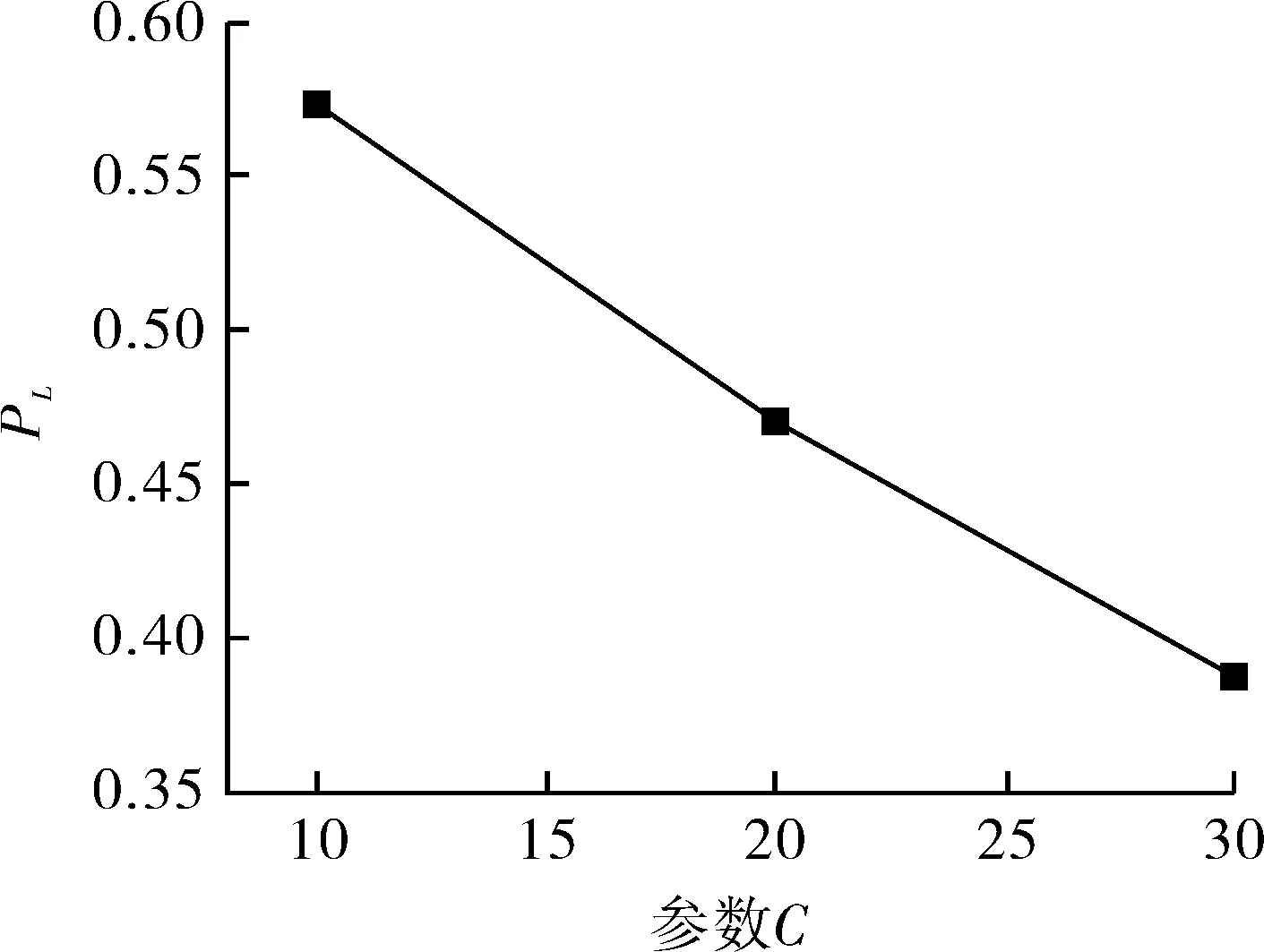
(c)尺寸参量C对PL的影响 (d)尺寸参量D对PL的影响图8 几何参数边际均值对无量纲极限内压PL的影响Fig.8 Influence of the geometric parameter marginal mean on the dimensionless limit internal pressure PL
取尺寸参数进行模拟试验,将模拟结果与公式计算值对比得到结果如表4及图9所示。
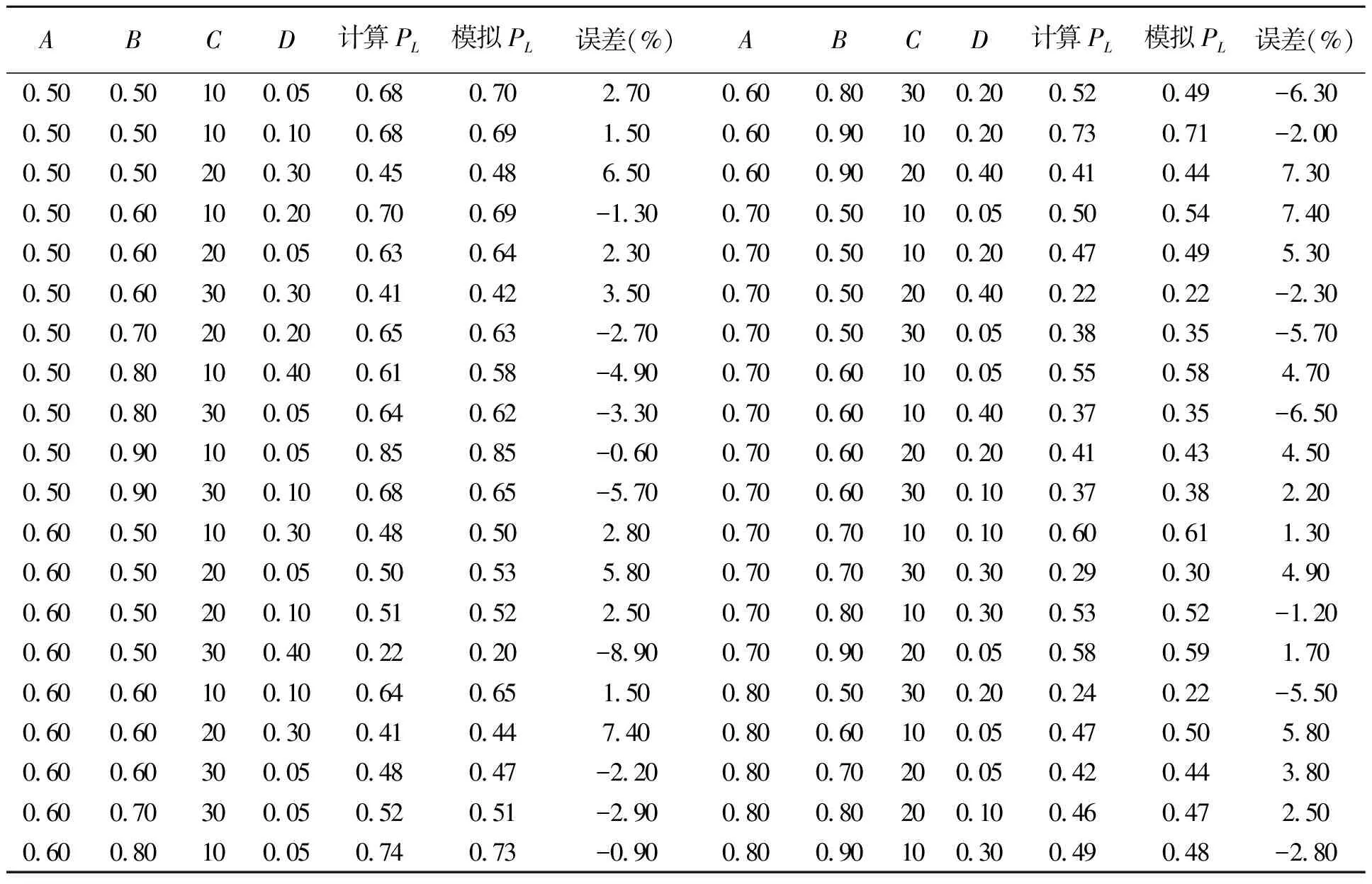
表4 验证试验数据汇总Tab.4 Summary of validation test data
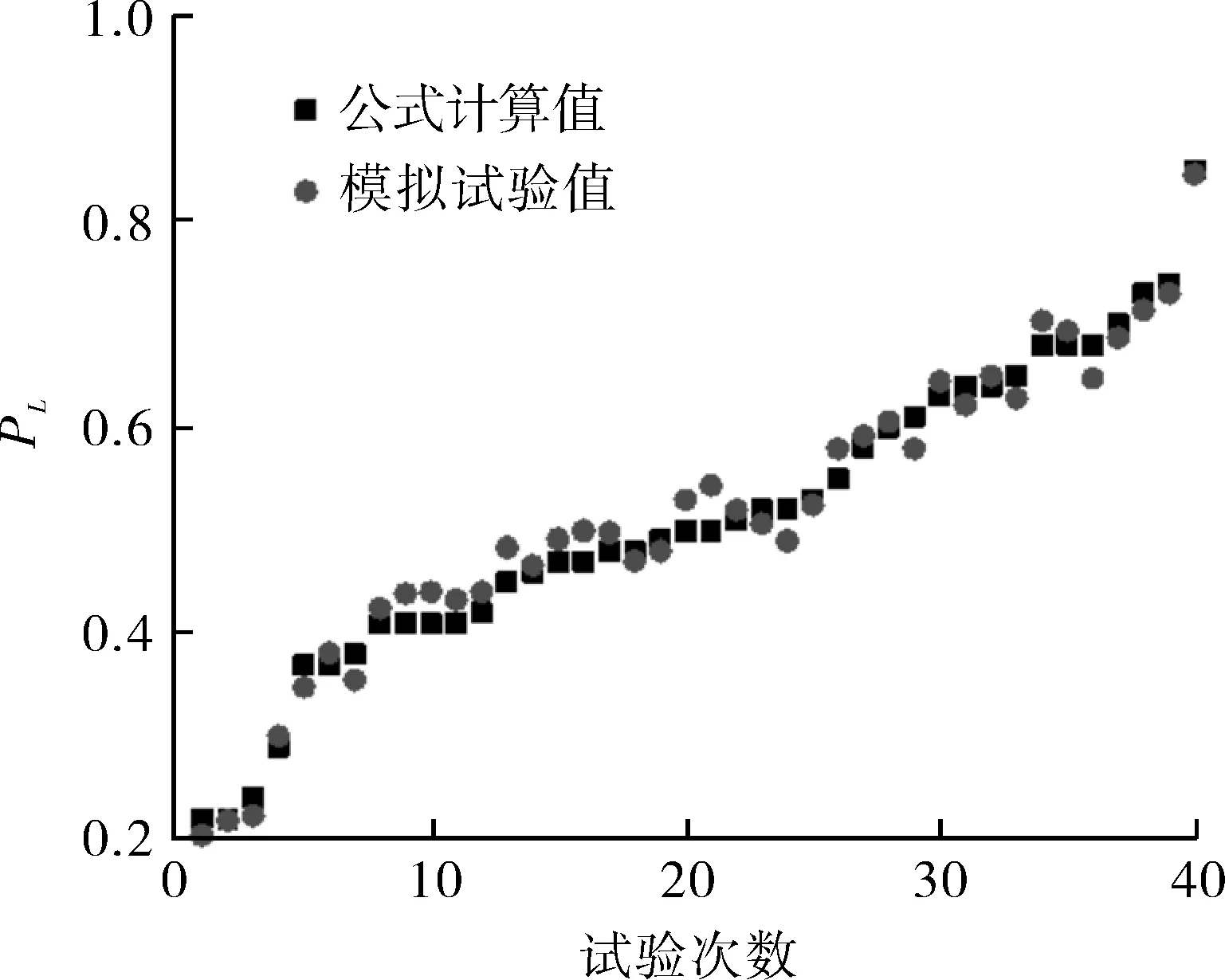
图9 极限载荷模拟结果与公式计算值对比Fig.9 Comparison of limit load simulation resultsand formula calculation values
对比极限载荷模拟结果与拟合公式计算值可发现,二者的数值误差不超过10%,由图9可以看出,每一组计算值与试验值基本接近,由此可见拟合公式能够用于内压下异径四通塑性极限载荷的估算。对比文献[7]提出的四通塑性极限内压拟合公式,将表3数据重新验算,得出r/D≤0.2时,估算式相差不大;r/D>0.2时,本文所提估算式更为准确。
3 结论
(1)通过分析无缺陷异径四通不同部位应力分布的差异性,得出变形量过大是异径四通在内压作用下破坏的主要原因。四通肩部内壁及腹部外壁首先达到屈服,随着内压的增大塑性区逐渐沿相贯线及壁厚方向扩张,且肩部先于腹部达到屈服。
(2)设计混合正交试验,分析得出本文涉及4个几何参数的对极限载荷PL具有显著影响,参数A=d/D,B=t/T,D=r/D对极限载荷PL为负向影响,C=D/T对极限载荷PL为正向影响,影响最大几何参数为主支管壁厚比。
(3)对正交试验结果进行数据拟合,得出内压下四通塑性极限内压工程估算式,采用大量模拟试验与拟合估算式计算结果对比,验证工程估算式的可行性,进而为后续四通管件优化设计和含缺陷结构的完整性评定提供参考。

