栅格结构激光焊接失稳有限元分析*

张景祺 ，林 健，雷永平，肖荣诗，李 龙，宋 征

（1.北京工业大学，北京 100124；2. 太原航空仪表有限公司，太原 030006；3. 首都航天机械有限公司，北京 100076）

准直器是航天探测活动中卫星望远镜的关键器件，其作用是调整空间射线的传播方向，为其他光学设备提供平行光源[1–2]。典型准直器的基本结构单元是由超薄金属板相互交叉组合成的栅格通孔，其制备过程中的关键工序为对两薄板十字交叉处进行的激光点焊连接。受卫星空间资源约束，由超薄金属板（厚度<0.1mm）对插点焊而形成的中能准直器的占空比需大于90%。而由于薄板刚度较小，在焊接制造过程中易产生失稳变形，严重影响了其制造精度[3–4]。目前，针对此类焊接变形问题的相关研究大多通过试验和数值模拟两种途径来开展。闫俊霞等[5]将二维热–弹–塑性数值模拟与三维薄板模型的屈曲分析方法进行结合，通过弹性屈曲计算，求出焊接后薄板的失稳变形量，并讨论了减少薄板结构焊后失稳变形的措施。季良等[6]通过试验方法研究了由厚度仅为0.07mm的超薄金属板组成的十字交叉结构的激光点焊工艺范围，研究结果表明当激光脉冲宽度为8ms，功率为0.2～0.32kW时十字交叉结构的焊点成型良好。Wang等[7]对船体薄板焊接结构中的典型接头进行了焊接仿真与试验验证，根据计算得到的固有变形作为弹性有限元分析的基本输入，预测了有横纵向加筋的薄板结构的面外变形与其临界失稳条件。曹政等[8]通过搭建专用装置，模拟了有密集焊缝的薄壁结构在高频随焊冲击作用下的光纤激光焊制造过程，结果显示随焊冲击作用可大幅降低06Cr19Ni10材质圆筒形薄壁构件在多道焊接制造后的尺寸收缩量，其值由0.95mm可减小到0.29mm。目前的研究中对金属超薄板组装结构的焊接变形，尤其是对激光点焊引起的超薄板失稳变形的仿真研究还较少。

本研究借助ABAQUS有限元计算工具，提取激光点焊热–力耦合数值模型中焊后残存的固有应变，作为特征值屈曲分析以及后屈曲分析的位移载荷，对两种激光点焊热输入下超薄板十字交叉接头的失稳变形模式进行了分析，在此基础上又研究了焊接顺序，焊点个数对整体栅格结构激光点焊屈曲变形的影响。该数值模型的应用对于揭示栅格结构在点焊装配过程中面外变形的发展规律，优化栅格结构的制造工艺，降低试验成本具有一定的指导意义。

数值模型

1 有限元模型

某种小视场准直器由4块横向排列（Z向）的薄板和4块纵向排列（Y向）的薄板对插点焊形成，总共由9个矩形栅格组成[9]。十字交叉点焊接头是此栅格结构的基本单元，首先建立了由长度均为68mm，宽度分别为4.68mm和1.17mm的两块厚度为0.07mm薄板中心交叉形成的十字点焊接头有限元模型，如图1所示，ABAQUS中采用壳单元S4R微分该模型，网格总数为7164，节点总数为5332。由于模型整体较长，仅在点焊端附近采用了较密的网格划分方式，将模型材料设定为参数随温度非线性变化的316L不锈钢[10]。模型的边界条件位于底部十字交叉点处，将其全约束来阻止模型的位移或旋转。在模型上取A～E作为数据提取路径ABC和ADE线段的端点。

以薄板十字交叉点焊模型为基础，继续建立了用于对整个栅格结构进行全过程屈曲分析的模型，如图2所示，模型中Y方向4个金属薄片排列间隔为1.17mm，Z方向4个金属薄片排列间隔为4.68mm，4个纵向构件和4个横向构件相互交叉固定，形成9个长×宽为1.17mm×4.68mm的长方形栅格，模型中网格总数为183224，节点总数为113714。边界条件设定在栅格结构底面边缘处的4 个薄板交叉顶角点处施加的全约束。有限元计算假设母材及焊缝为连续固体，在固体力学范畴内进行分析。塑性区材料行为服从塑性流动法则和硬化法则。

图2 准直器栅格结构示意图Fig.2 Schematic diagram of grid structure of collimator for medium energy telescope

2 激光点焊热源模型

根据薄板激光焊接功率密度高、能量集中、焊缝成型窄的特点，模拟中焊接热源模型采用半球状热源模型，如图3所示，半椭球热源中任意一点的功率密度：

图3 半球体热源模型Fig.3 Hemispherical heat source model

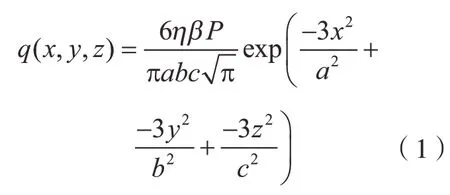
其中，η为吸收率；a、b、c分别为半椭球的形状参数；P为功率；β为占空比系数，根据试验中点焊熔池测量数据和仿真计算结果，两种典型激光加热功率的热源参数设定如表1所示。

表1 热源模型参数Table 1 Parameters of heat source

3 十字交叉模型激光点焊后固有应变的提取

在较低点焊功率（200W）和较高点焊功率（320W）参数下热–力耦合模拟激光点焊得到的十字交叉薄板结构附近的残余压缩塑性应变场进行固有应变提取[11]，如图4所示，观测了平行于激光束方向（过两薄板交点沿热–力耦合模型Z向）的纵向压缩塑性应变和薄板横截中面方向垂直于激光束方向的横向压缩塑性应变的分布。可见随着点焊功率的增大，固有应变分布的深度和宽度有所拓宽，但整体分布形态基本一致，整个压缩固有应变区主要存在于焊点附近宽约2mm、深约1mm的位置。

图4 低热输入与高热输入下超薄板激光点焊接头的固有应变分布Fig.4 Schematic diagram of grid structure of collimator for medium energy telescope

简化热–力耦合模拟所得残余压缩固有应变在屈曲模型中的分布，如图5所示，焊点处的固有应变区域可以近似认为是由几个关于激光束所在直线轴对称分布的矩形带状区域组成，所以可将薄板面内的横向和纵向塑性应变所在区域分别由绿色区和蓝色区标识，红色数字代表高热输入下的应变分布尺寸，黑色数字代表低热输入下的应变分布尺寸。对单个焊点附近的纵向压缩应变和横向压缩应变的值进行积分汇总，求出均值，如表2所示。

从表2数据可知，高热输入算例其纵向压缩残余应变值是低热输入算例纵向应变值的2倍多。而对于薄板十字交叉形成的点焊结构，其板内残余应变场分布具有绕点焊激光束旋转90°重合的特点，将接头附近区域材料在模型纵向（X）和横向（Y或Z）上的固有应变均值设置为热膨胀系数，再在模型中相应位置施加单位负温度载荷，实现交叉点的收缩位移边界条件来进行以固有应变为输入载荷的特征值屈曲分析，屈曲分析以固有应变区域的热膨胀系数和尺寸来区分为低热输入和高热输入两个算例[12]。

表2 激光焊点附近压缩塑性应变均值Table 2 Mean compressive plastic strain near laser solder joint

激光点焊屈曲变形的分析结果

1 十字交叉结构的点焊屈曲变形

首先运用特征值计算方法得到了较低热输入下屈曲变形在两块交叉薄板U2（屈曲模型坐标轴Y向）和U3方向（屈曲模型坐标轴Z向）的分布，如图6所示，可见首阶正特征值所对应的两块薄板上的面外变形模态总有一种处于主导状态（即云图中最大位移分量为1.0），而另一种则较微弱。从位移分量来看，较长薄板的面外变形幅度大约是较短薄板的3.5倍。

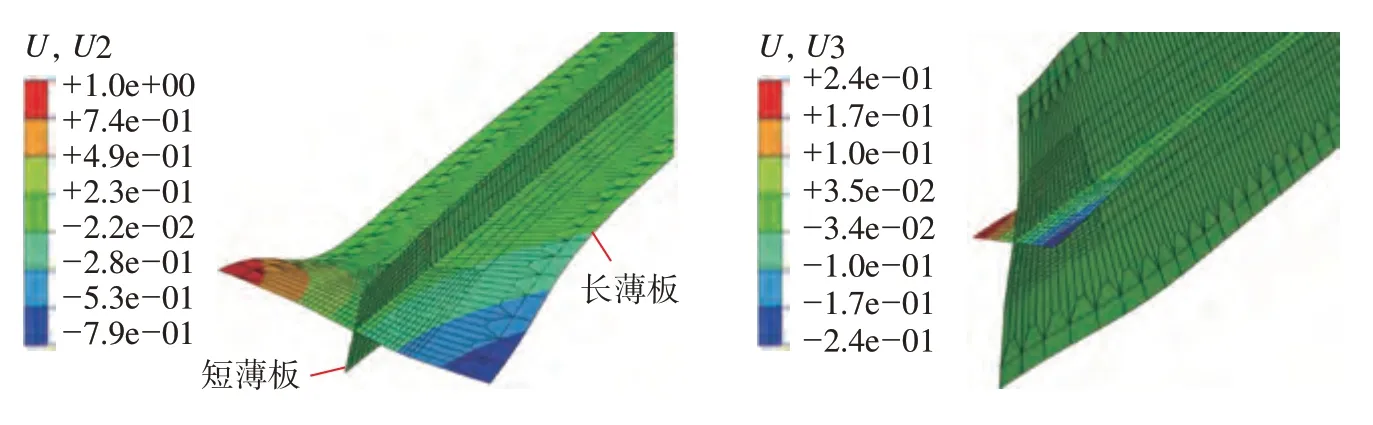
图6 低热输入下两块薄板的面外屈曲变形（特征值分析结果）Fig.6 Out-of-plane buckling deformation of two thin plates under low heat input

在较高热输入下的两交叉薄板的首阶正特征值所对应的屈曲模态也表现为在焊点两侧分布有一侧上凸，一侧下凹的偏转变形，如图7所示，相比于低热输入下的算例，此时两薄板的面外偏转方向正好相反。且其屈曲特征值较小，约为低热输入下的1/3，而点焊结构中较长薄板的面外变形幅度是较短薄板的3倍。

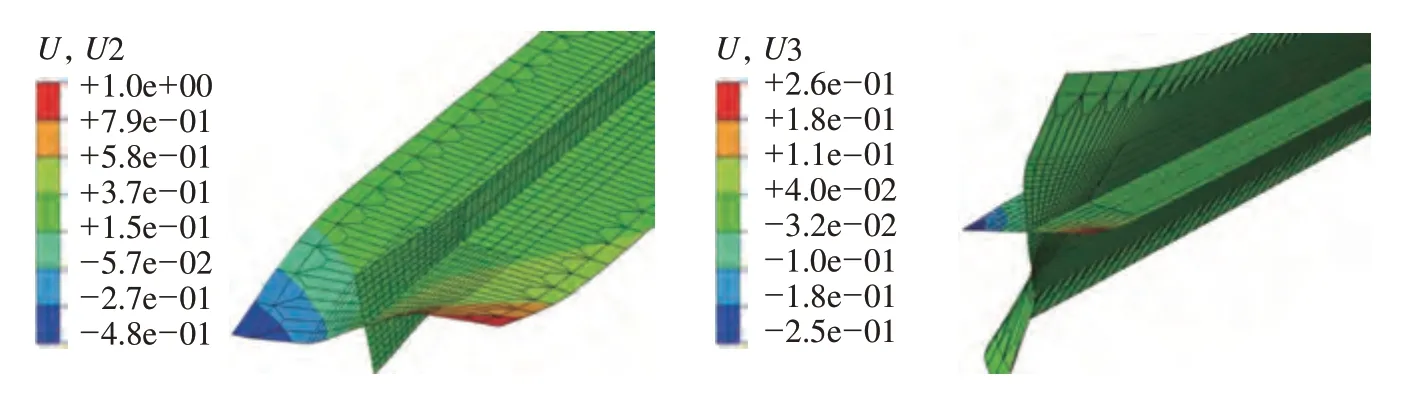
图7 高热输入下两块薄板的面外屈曲变形（特征值分析结果）Fig.7 Out-of-plane buckling deformation of two thin plates under high heat input

以第一阶正特征屈曲模态作为初始变形加载于模型，对十字交叉薄板结构进行后屈曲变形分析来获得具体的面外变形量与分布，发现交叉薄板点焊模型的后屈曲变形基本上维持了初始的偏转变形模式，如图8所示，高热输入激光点焊模型中凸起区域面积略大于凹下区域，而凸起变形极值小于凹下变形极值。

图8 后屈曲分析得到的交叉点处薄板的面外变形（P=320W）Fig.8 Out-of-plane deformation of thin plate at intersection obtained by post-buckling analysis（P=320W）

沿图1中位于薄板模型边缘的ABC折线段路径提取后屈曲模型U2方向的变形，沿ADE折线段路径提取模型U3方向的变形。对320W和200W两种热输入下交叉薄板在两个方向的面外变形分布进行了对比分析，如图9所示。可见两种热输入下接头处的屈曲变形都呈现随距焊点距离增大先增加后减小的趋势，高热输入试样U2方向变形最大值为7.48μm，U3方向变形最大值为–2.88μm。低热输入试样U2方向变形最大值为–5.56μm，U3方向变形最大值为1.53μm。从面外变形的分布范围来看，较宽薄板上的面外变形在距接头7mm深处消失，较窄薄板上的面外变形在距接头6mm深处消失。

图9 后屈曲分析得到的沿两条路径薄板的面外变形值对比Fig.9 Comparison of out-of-plane deformation values of thin plates along two paths obtained by post-buckling analysis

对0.07mm超薄板十字交叉结构进行相应参数的激光点焊试验，从激光束入射方向观察该结构的面外变形，如图10所示，其中图10 （a）为较高热输入下的点焊试样，图10（c）为较低热输入下的点焊试样，图10（b）和（d）分别为对图10（a）和（c）中焊点附近面外变形的简化描述，红色虚线代表薄板初始位，蓝色实线代表激光点焊后薄板变形位。高热输入下两块交叉薄板在焊点附近区域都出现了偏转形式的面外屈曲变形，而低热输入下的薄板变形主要发生在交叉薄板中的一块上，也表现为偏转变形，且变形方向与高热输入相反，综上可知模拟与试验结果中薄板结构变形的趋势相同。

图10 不同激光热输入下的焊接面外变形Fig.10 Out-of-plane deformation of welding under different laser heat input

2 焊接顺序对栅格结构屈曲变形的影响

薄板栅格中多个交叉点处的激光焊是按一定顺序进行的，尽管最终焊点的位置已经确定，但不同的焊接顺序改变了点焊过程中的焊点分布，使各个固有应变区的相互作用方式改变，进而通过影响焊接过程中出现的局部屈曲变形分布也最终改变了整体结构的失稳变形。首先将栅格结构16个焊点中的前4个焊点的分布方式作为变量，如图11所示，点焊顺序1中4个焊点沿Z方向直线分布，点焊顺序2中4个焊点沿Y方向直线分布。

图11 4种不同点焊顺序后的焊点分布情况Fig.11 Solder joint distribution after four different spot welding sequences

在4个焊点分布位置添加相应的固有应变载荷进行特征值屈曲变形分析。因为栅格结构的Y向和Z向的面外变形对准直器的占空比有较大影响，重点关注在这两个方向的屈曲变形。两种焊接顺序下的临界特征值（EV）和其对应的首阶正特征值屈曲模态如图12所示，发现栅格结构的面外变形主要位于沿Y向排列的金属薄片上，表现为以沿Z向排列的薄板为边界的小范围内的鼓凸和凹陷变形，两者在焊点分布方向交错出现。

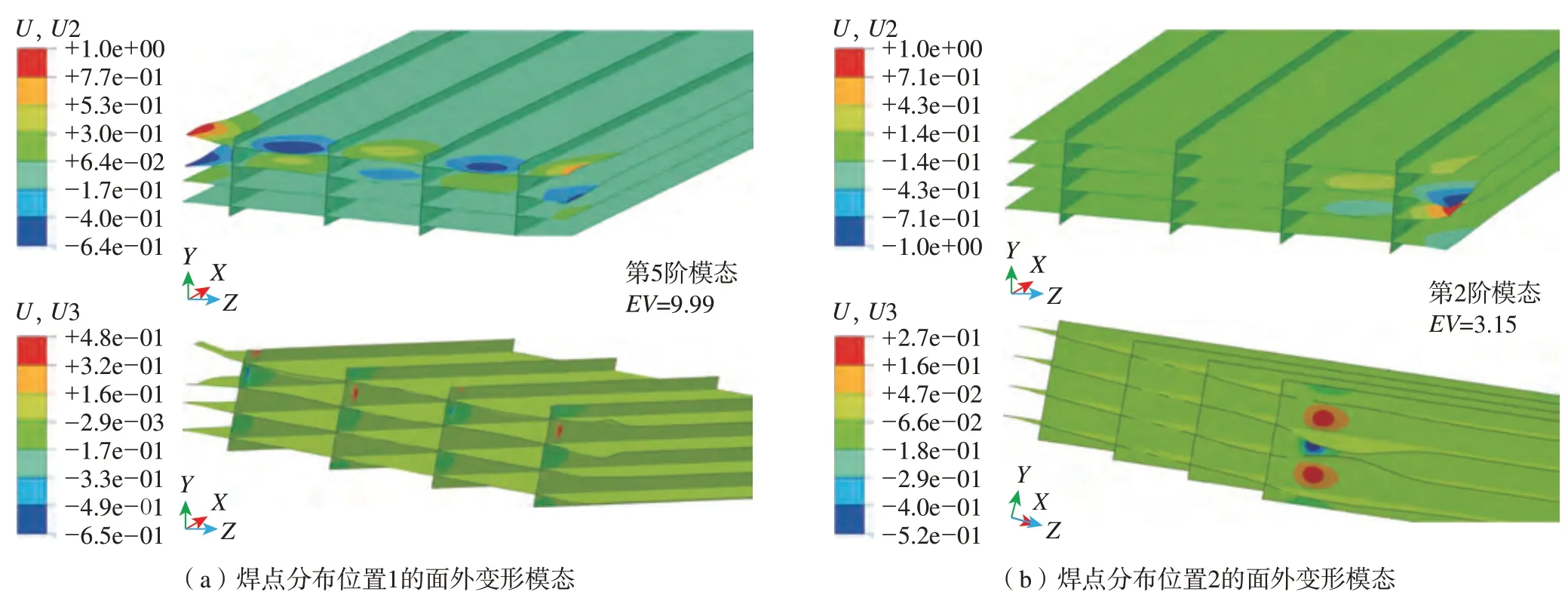
图12 两种焊点分布对变形模态的影响Fig.12 Influence of two kinds of solder joint distribution on deformation mode

对焊点分布位置1的模型以第5阶屈曲模态即首阶正特征值屈曲模态为初始变形进行了后屈曲变形计算，得到实际面外变形量如图13（a），可见此时面外鼓凸变形量最大可以达到5.7μm左右，第一层薄板接头处有明显的整体向下偏移。以主要面外变形方向上的最大正位移减去最大负位移作为栅格的失稳挠度，此算例的失稳挠度为27μm。从上至下分别在4块横向薄板边缘建立数据取点路径a–d，得到面外变形量随4条路径的变化曲线如图13（b）所示，可见此时在上两层薄板分布着较为明显的大波浪变形，而底部两层薄板也有较小的面外变形分布，且两者的变形趋势相反。

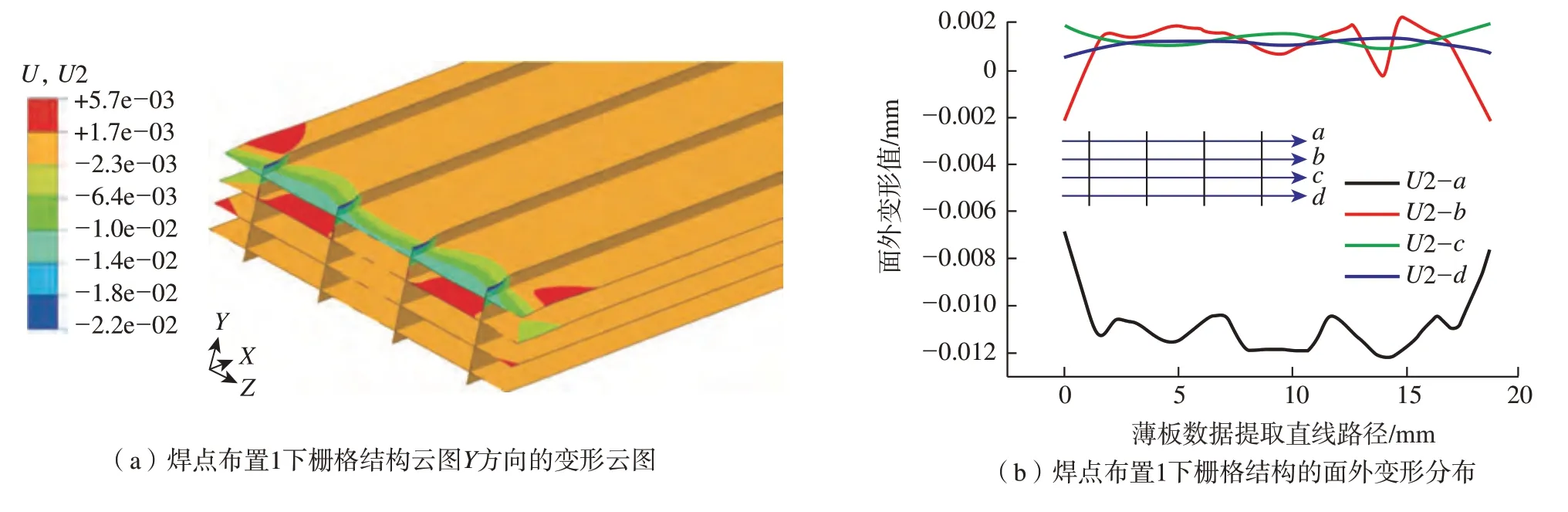
图13 焊点布置1可能引起的薄板栅格失稳变形Fig.13 Grid instability deformation of thin plate caused by solder joint arrangement 1

同理，对焊点分布位置2的模型的失稳变形量进行了计算。如图14（a）所示，此时栅格的失稳挠度较上个算例变大，约为35μm。由于各焊点固有应变作用区的距离较为接近，局部区域产生了较大的压应力，使变形量加大。在之前建立的路径a–d上提取Y方向的变形数据U2，并在4个焊点所在的纵向薄板的边缘处取点建立的沿Y方向的直线路径e上提取Z方向的变形数据U3，如图14（b）所示。可以看出，此时沿Y向分布的第1层和第4层的薄板变形方向相反，而变形趋势相同。随着4个焊点在Y向的布置，相应薄板的Z方向出现了波浪状的起伏变形，凸起变形量略大于凹下变形量。

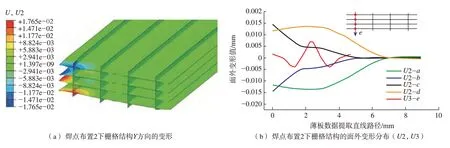
图14 焊点布置2可能引起的薄板栅格失稳变形Fig.14 Possible grid instability deformation of thin plate caused by solder joint arrangement 2

3 焊点数量对栅格结构屈曲变形的影响

由上节可知，第1种点焊顺序下（焊点沿模型Z向直线分布）栅格结构的变形量较小，整体失稳挠度可以控制在28μm左右，以此为基本的焊接顺序，设定了对16个薄板交叉处的激光点焊的具体顺序如图15所示，依次完成构件的最终点焊固定连接。栅格结构中的焊点个数会随着焊接的进行而逐渐增多，使处于各个阶段的栅格内部的固有应变载荷量不同，不同点焊阶段的屈曲变形模式也会有差异。

图15 包含焊点个数不同的4个点焊阶段Fig.15 Four spot welding stages with different number of solder joints

设定点焊功率为320W，在各阶段所对应的焊点附近加载该热输入下的固有应变参数，进行多个特征值屈曲计算，结果如图16所示，其中图16（a）为完成2个焊点后的屈曲模态，图16（b）为6个焊点时的屈曲模态，图16（c）为8个焊点时的屈曲模态，图16（d）为16个焊点即焊接完成时的屈曲模态。随着固有应变区域的累加，不同焊接阶段的失稳模态出现改变，当焊接阶段进行到第4步时，屈曲变形已经拓展到接头附近的所有区域。此时结构的屈曲变形主要发生在沿y向分布的4块薄板的中间两块薄板位置，对于悬空的薄板空间，屈曲变形的发展趋势具有随机性，多个焊点附近屈曲变形的相互耦合作用会使栅格结构在中间区域的面外变形量相比顶部和底部区域有明显增大。

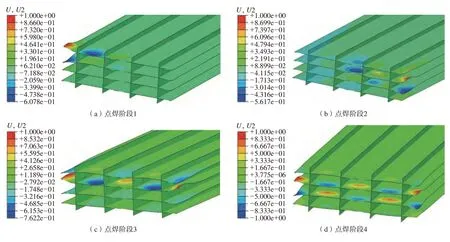
图16 薄板栅格在各点焊阶段所出现的屈曲模态Fig.16 Buckling modes of thin plate grid in each spot welding stage

继续计算处于各点焊阶段之间多个焊点个数下栅格结构的首阶正屈曲特征值，并记录了其所对应的屈曲模态阶数，如表3所示，焊点个数的增多使结构整体的固有应变增加，屈曲特征值持续下降，失稳变形也会更易发生。如图17所示，该栅格结构的屈曲特征值λ随焊点个数b增加而变化的规律可由波尔兹曼函数进行拟合。

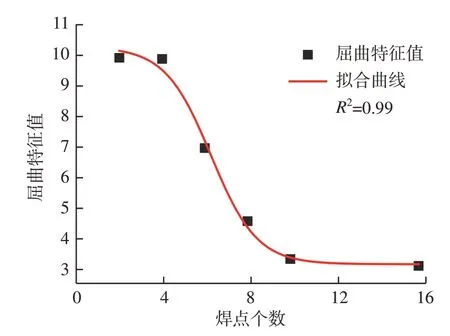
图17 栅格结构屈曲特征值与焊点个数的关系Fig.17 Relationship between buckling eigenvalues of grid structures and number of solder joints

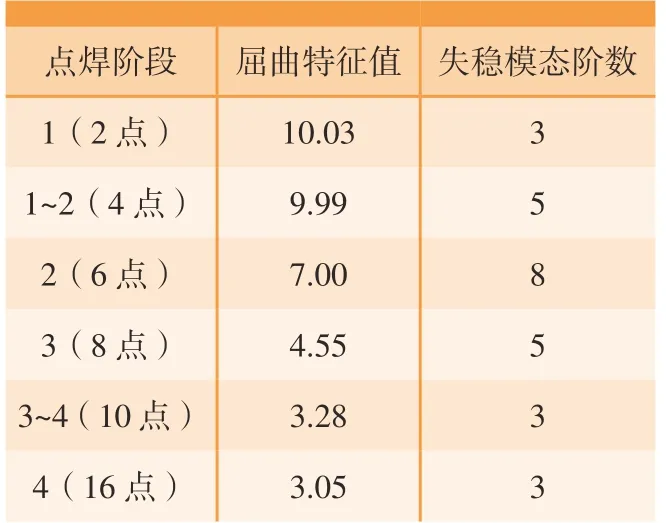
表3 不同点焊阶段栅格结构的屈曲特征值Table 3 Buckling eigenvalues of grid structures in different spot welding stages

结论

（1）对热–力耦合模拟得到的单个焊点附近的纵向压缩应变和横向压缩应变的值进行积分汇总，得出十字接头横向塑性应变平均值在200W时为–1.39×10–2，在320W时为–1.72×10–2，纵向塑性应变在200W时为–9.69×10–4，在320W时为–2.13×10–3，可进行以固有应变为输入载荷的特征值屈曲分析。

（2）两交叉薄板的点焊屈曲模态表现为在焊点两侧，一侧上凸，一侧下凹的偏转变形，较高热输入算例相比于低热输入算例，两薄板的面外偏转方向正好相反。高热输入试样U2方向变形最大值为7.48μm。低热输入试样U2方向变形最大值为–5.56μm。较宽薄板上的面外变形在距接头7mm深处消失，较窄薄板上的面外变形在距接头6mm深处消失，模拟与试验结果具有相同的变形趋势。

（3）采用焊点沿模型Z向直线分布的焊接顺序进行点焊时栅格结构的失稳变形量较少，对该种模型以第5阶屈曲模态为初始变形进行了后屈曲变形计算，此时面外鼓凸变形量最大可以达到5.7μm。随着固有应变区域的累加，不同焊接阶段的失稳模态出现改变，最终多个焊点附近屈曲变形的相互耦合作用会使栅格结构在中间区域的面外变形量相比顶部和底部区域有明显增大。