微型涡桨发动机动力涡轮叶片与机匣碰撞失效仿真分析

李纪永 李颖新 马阳 李芳 胡凯

微型涡桨发动机动力涡轮叶片与机匣碰撞失效仿真分析

李纪永 李颖新 马阳 李芳 胡凯

（四川航天中天动力装备有限责任公司，成都 610100）

针对某微型涡桨发动机试车过程中出现的叶片断裂及机匣包容性问题，利用接触-碰撞动力学方法模拟了单叶片断裂后对叶片和机匣的碰撞失效过程，对碰撞位置、碰撞中的能量变化、等效应力/应变等进行了分析。结果表明，单涡轮叶片断裂情况下，叶尖和叶根依次与机匣碰撞产生两个撞击点，不考虑其余叶片的影响下，第一个撞击点由于叶尖滑动耗散部分能量，第二个碰撞点受到的冲击更大。考虑整周涡轮叶片旋转情况，断裂单叶片受后方旋转叶片驱使，动能大幅增加了，第一个碰撞点造成冲击更大。因此，在机匣包容性分析中，需考虑其余旋转叶片增强断裂叶片动能的影响。

涡轮叶片；机匣；接触-碰撞动力学；包容性

0 引言

高温高转速是动力涡轮式微型涡桨发动机的典型特点，热端旋转部件叶片断裂失效出现的概率极高，其危险性也最大。高转速涡轮转子造成的机匣包容性问题更严重，热端机匣包容问题非常复杂，毫秒级时间尺度内发动机转/定部件间发生多属性非线性动力学相互作用。对于动力涡轮式涡桨发动机，动力涡轮—传动系统—负载是相互耦合的，动力涡轮叶片断裂，传动系统齿轮瞬间过载冲击，对发动机造成比较大的损伤，若叶片飞出则会对试验设备造成很大的损害[1-5]。机匣包容性设计及破坏模式研究得到诸多关注，谢文涛[6]利用LS-DYNA与试验结果对比分析机匣包容能力，表明运用LS-DYNA软件开展动力涡轮整圈叶片断裂脱落和撞击机匣过程较为接近试验，优于包容系数方法等计算方法，为数值模拟方向提供参考。张晓峰[7]从机匣撞击痕迹分析了断裂叶片飞出后的飞行方向及撞击次数，叶片弯曲对包容性产生较大影响。Deng[8]进行了圆头弹体以低俯仰角撞击铝合金靶板的包容性试验，将试验和仿真结果对比，验证了仿真分析中靶板的失效模式和裂纹扩展的准确性，并分析了弹体打靶姿态角和速度对撞击轨迹造成的偏差。刘闯[9]等采用试验方法获取了叶片的飞断转速、冲击载荷、轴心轨迹和机匣受到撞击后的动态相应。Astrid和Jorg[10]在利用LS-DYNA对旋转试验设备上进行的涡轮机匣包容性试验进行了仿真计算，考虑到仿真的精确性，数值模拟过程中考虑了相邻叶片间的相互影响、断裂叶片的外貌形状、高速冲击下的失效准则以及应变率的影响。在机匣包容性试验分析中，很少全部考虑叶片撞击时的姿态角（包括俯仰、偏航及滚转）以及叶片间的干涉，将叶片直接冲向靶板难以真实反映机匣破坏程度与模式，相对来说，涡轮机匣包容性的研究较少，尤其是涉及到高温及高应变率下的失效行为，因此开展动力涡轮机匣的包容性研究十分重要。本文通过计算及故障试验研究了单叶片断裂、全叶片断裂情况下叶片及机匣的损伤行为，分析了碰撞过程中能量、应变等变化模式，对涡桨发动机的工程应用及研究具有重要的指导意义。

1 接触模型

动力涡轮与机匣接触行为含两个基本接触类型：法向和径向。法向接触利用“硬”接触模拟，其描述如图1所示，当未接触时，压力为0，当接触时，接触压力为计算值。

图1 法向接触模型

切向接触采用库伦摩擦模型，使用罚函数法的各向同性库仑摩擦罚函数，刚度自适应调节，理性情况下刚度无穷大，如图2所示。

图2 切向接触模型

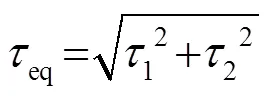
2 结构损伤

2.1 高温机匣材料Johnson-Cook本构及失效模型

Johnson-Cook本构模型以乘积的形式描述了应力与各影响因素之间的关系，包括材料的加工硬化效应、应变率效应和温度软化效应，如式（2）所示，其中，等式右边第一项表示室温下准静态应力－应变关系，即塑性应变硬化；第二项表示应变速率硬化项；第三项为温度软化项。具体表达式为

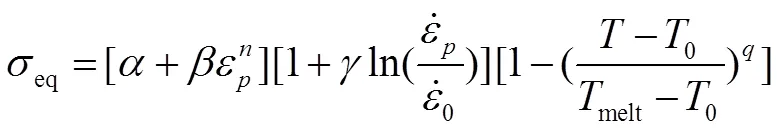
表1 GH4169材料J-C本构参数

Johnson-Cook模型中的断裂判据为

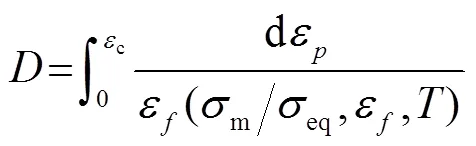
等效断裂塑性应变则使用应力三轴度、塑性应变率和温度表示，Johnson-Cook失效模型描述了一种损伤参数与材料参数非耦合的各项同性的材料硬化行为，其硬化函数包括塑性应变硬化、应变速率硬化和温度软化三个部分。如式（4）所示：

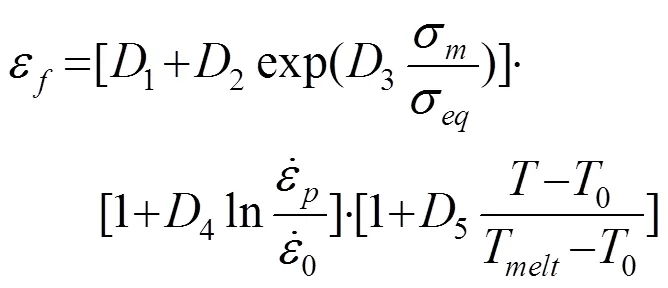
其中，等式右边第一项表示室温下准静态应力－应变关系，即塑性应变硬化；第二项表示应变速率硬化项；第三项为温度软化项。其中，1，2，3，4，为材料常数。式中，应力三轴度、塑性应变率和温度的影响为三个相互独立的公式，而等效断裂塑性应变表卡为这三个独立公式的乘积。忽略塑性应变率的影响和温度的影响，假设应力三轴度接近于0，进行泰勒级数展开

由于Johnson-Cook失效模型不仅考虑了静水压力对于材料断裂的影响，而且阐释了塑性应变率和温度对韧性断裂的影响规律，建立了临界断裂应变与应力三轴度、塑性应变率和温度的函数关系，能够较好的模拟机匣受撞击破裂的情况。

表2 GH4169材料J-C失效模型参数

2.2 涡轮叶片材料本构模型及剪切损伤模型

涡轮叶片材料为镍基高温合金K424。文献[13]通过非线性各项同性硬化模型拟合出真应力—真塑性应变曲线

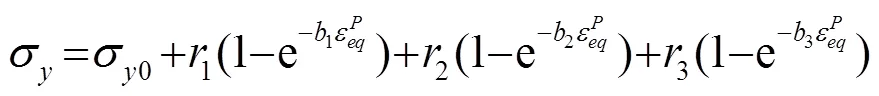
表3 K424拟合本构模型参数

传统大变形有限元分析中，K424 优化本构模型对缺口试样极限拉伸强度具有较好的预测精度。根据文献[12]基于K424优化本构模型建立材料的连续损伤力学模型，根据断裂应变优化连续损伤力学模型参数，得到软化系数方程为：

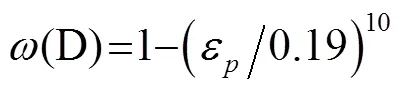
3 单叶片冲击机匣计算分析

建立单叶片有限元模型，如图3所示。计算过程：在1ms时刻前，涡轮叶片转速由0rad/s提高到4800rad/s；1ms时刻断裂叶片释放。对于完整叶片模型，其余完整叶片保持转速4800rad/s。

未对释放自由度后的叶片进行约束，图4、图5分别为整个碰撞过程的动能曲线和内能曲线，根据上述图4、5曲线可以看出：0～0.9ms时间段，涡轮叶片动能由0增加大最大值；0.9～1ms时间段，转速和动能保持稳定；1ms时刻，断裂叶片脱落，经过0.06ms后（即1.06ms时刻）断裂叶片叶尖与机匣发生接触，叶尖在机匣内曲面滑移，接触位置机匣变形，叶片动能转换为内能，1.12ms时刻，叶尖停止滑移，此时断裂叶片约48%的动能转换为内能；1.12ms～1.25ms时间段，叶片与机匣分离后向前运动，并在沿轴向旋转；1.25ms时刻，叶片叶根部位与机匣发生碰撞，到1.32ms时刻，叶片与机匣开始分离。叶片经历了脱离约束、叶尖碰撞（叶尖发生损伤来源）、翻滚、叶根碰撞、翻滚的过程，与常规试验不同，整个仿真考虑了叶片姿态的变化，运动过程如图6所示。

图3 单叶片模型

图4 叶片动能曲线

图5 内能曲线

碰撞能量转换过程本质是叶片动能与内能的转换（由于机匣固定约束，其动能曲线表征为叶片的动能）。根据图9可知，叶片初始动能为505J，第一次碰撞时损失48%的初始动能（242J），第二次碰撞时损失48.5%初始动能（245.3J）。两次碰撞过程中叶片损失的动能基本相同，但由于第一次碰撞过程中叶片与机匣发生了较大的滑移，摩擦耗散能量为31J，远大于第二次碰撞中的摩擦耗散能量（5J），而第一次碰撞过程的塑性耗散能量小于第二次塑性耗散能量，如图10所示。因此，第二次碰撞对机匣的损伤较大。

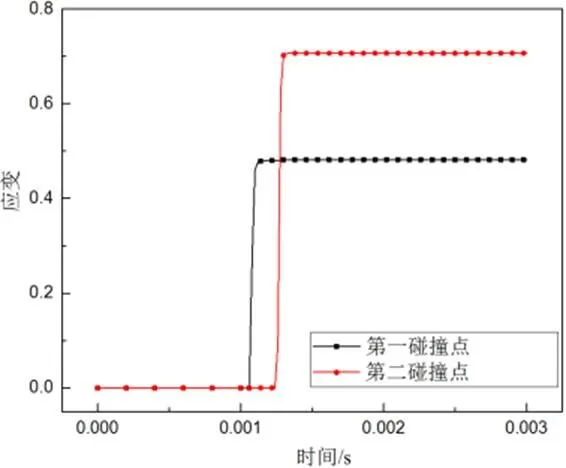
图8 撞击位置等效塑性应变

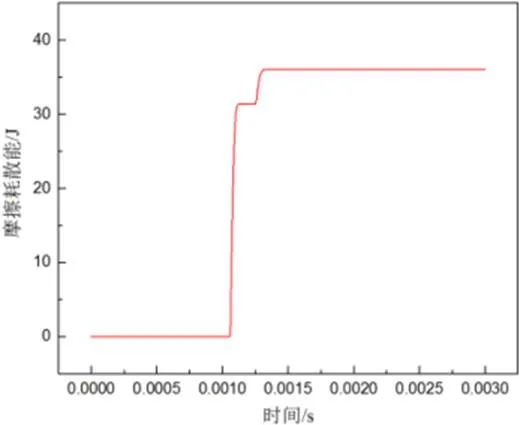
图9 摩擦耗散曲线

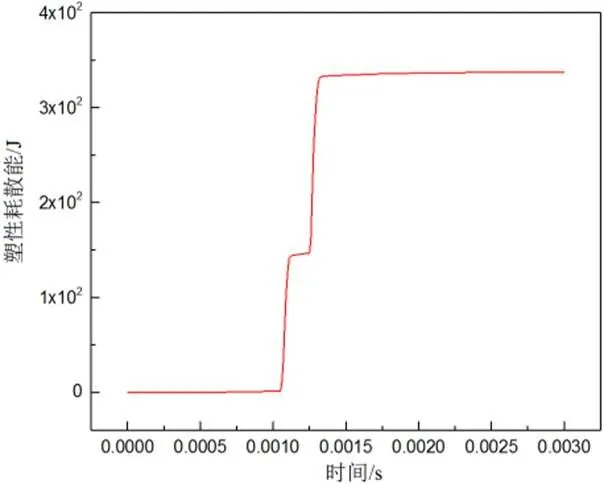
图10 塑性耗散曲线

4 考虑整周叶片对断裂叶片撞击机匣影响分析

4.1 计算分析

整圈叶片模型如图11所示，网格数量为226922。计算过程与单只叶片基本一致，不同的地方在于，只对一个叶片进行释放，其他叶片保持旋转不变。

图12、图13分别为整个碰撞过程的动能曲线和内能曲线（由于机匣固定约束，其动能曲线表征为叶片的动能）。根据曲线可以看出：0～0.9ms时间段，涡轮叶片动能由0增加大最大值；0.9～1ms时间段，转速和动能保持稳定；1ms时刻，断裂叶片脱落，经过0.06ms后（即1.06ms时刻）断裂叶片叶尖与机匣发生接触，叶尖在机匣内表面滑移，接触位置机匣变形，叶片动能转换为内能，1.12ms时刻，断裂叶片约50%的动能转换为内能；1.13ms时刻，减速的断裂叶片与后方的完整叶片碰撞，完整叶片加速断裂叶片使得机匣变形加剧，随后机匣破裂，动能在这一过程中波动并总体呈现增加趋势，内能在这一过程中增速显著提高，如图14所示；1.22ms时刻，断裂叶片与机匣第一次碰撞结束，同时，断裂叶片与后方叶片分离，断裂叶片旋转，此后一段时间系统动能和内能保持不变；1.32ms时刻，断裂叶片叶根与前方机匣碰撞，碰撞部位机匣产生塑性变形，断裂叶片动能急剧降低，叶片根部碰撞位置在冲击作用下破碎；1.4ms时刻，反弹的断裂叶片叶根位置再次与完整叶片碰撞。1.42ms时刻以后，动能基本保持稳定，碰撞过程结束。

图11 整圈叶片模型

图12 总动能曲线

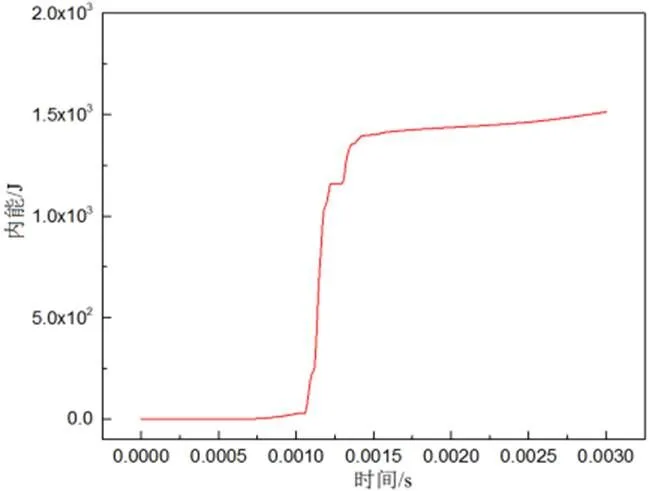
图13 总内能曲线

图15为系统对外做功曲线，在1ms之前涡轮转速由0rad/s增加4800rad/s，所做功大小为13100J，1.13ms时刻之后完整叶片以增加断裂叶片动能的形式对外做功。从叶片断裂到碰撞过程结束，完整叶片对外做功为1445J，其中，1.13ms～1.22ms（与断裂叶片第一次接触到分离的时间）时间段内做功为1408J，约为断裂叶片初始动能的2.8倍。由此可见，后方旋转叶片对断裂叶片碰撞大大的提高了断叶动能，加大了断裂叶片对机匣的破坏能力，导致机匣包容能力降低。图16为等效应力及机匣破坏分布情况，图17为机匣两次碰撞位置的等效塑性应变量对比情况，可以明显看出，第一次碰撞点等效塑性应变值明显大于第二次碰撞点等效塑性应变值，第一次碰撞破坏更大。

图15 对外做功能量

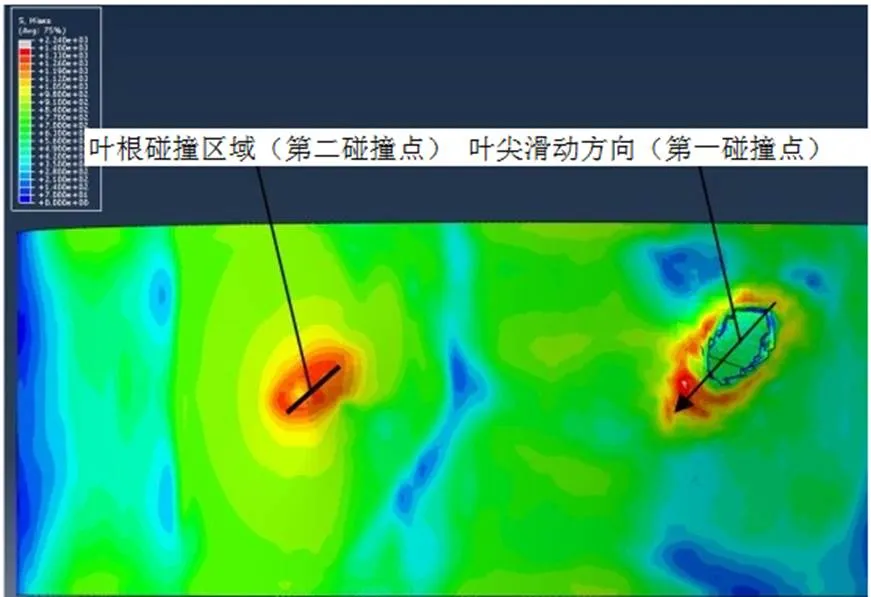
图16 等效应力分布

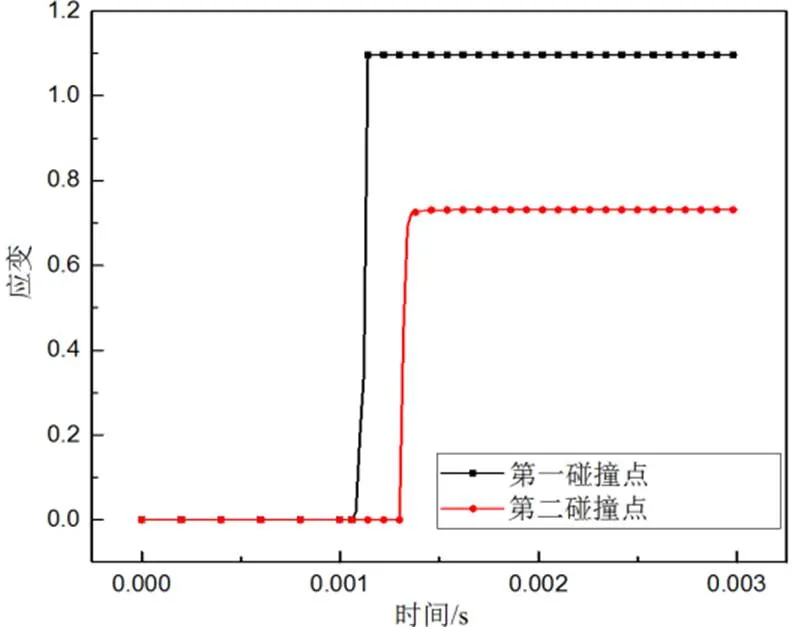
图17 碰撞位置等效塑性应变

4.2 故障试验对比分析

微型涡桨发动机为单轴动力涡轮式，动力涡轮位置如图18所示，在某次试验过程中，发生了叶片断裂故障，叶片并未全部断裂，其中一个叶片断裂情况如图19所示。通过图19可知，后面叶片冲击单只断裂叶片后，导致后面叶片间距变小，增大了断裂叶片的动能，其叶尖与机匣发生撞击碰摩，导致了叶尖部分缺失。其故障现象和考虑整周叶片的计算现象相符。

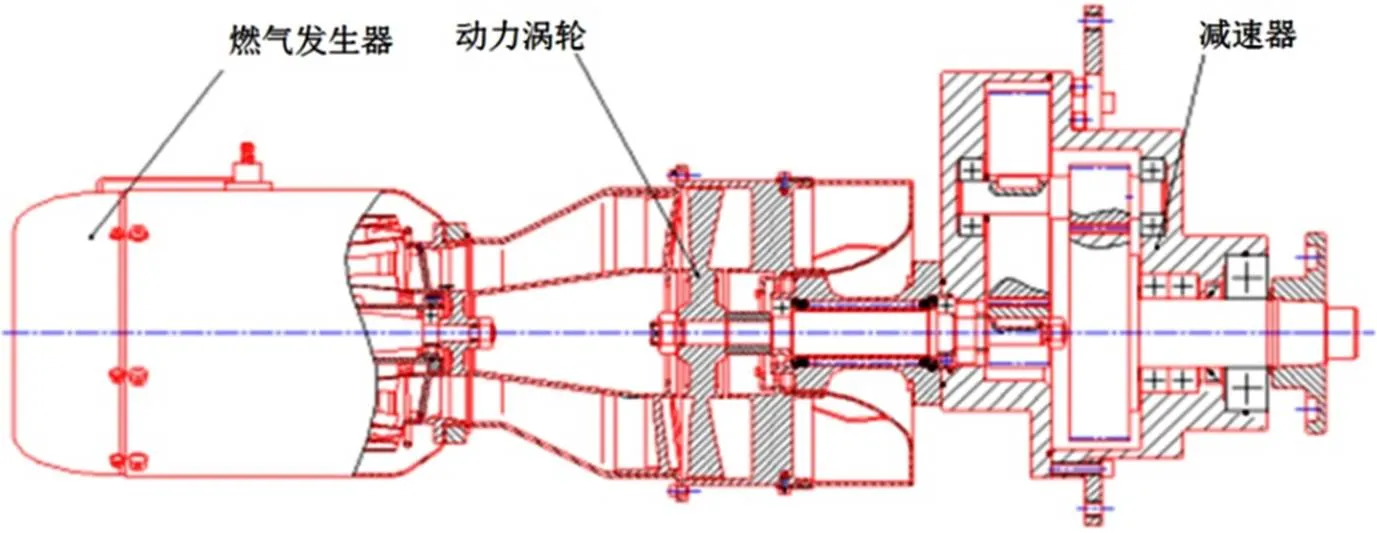
图18 微型涡桨发动机剖面图

图19 叶片残骸对比

5 结论

本文对比分析了两种不同模型下叶片断裂冲击机匣的影响。主要结论如下：1）发动机涡轮叶片断裂后，叶尖和叶根依次与机匣碰撞产生两个碰撞点，不考虑其余叶片影响的情况下，由于摩擦耗散能的影响，第二个碰撞点受到的冲击更大；2）考虑整周叶片运转情况下，旋转叶片对断叶产生较大冲击，驱使断叶沿旋转方向移动，引起断叶动能增加，提升断叶的破坏性，造成机匣包容性降低；3）整周叶片对机匣包容性能力的影响主要体现在增强断叶与机匣第一次碰撞的破坏能力，而对第二次碰撞影响较小。故在机匣包容性分析中，不可忽视其余旋转叶片提升断裂叶片动能的影响。

[1] Sinha S K, Dorbala S.Dynamic loads in the fan containment structure of a turbo fan engine [J].Journal of Aerospace Engineering, 2009, 22(3): 260-269.

[2] 吴振强, 李海波, 程昊, 等.热环境下金属壁板噪声激励动态响应试验研究[J].强度与环境, 2016, 43(2): 25-33.[WU Zhenqiang, LI Haibo, Cheng Hao, et al.Dynamic response tests of metallic panels excited by acoustic loads in thermal environment[J].Structure & environment engineering, 2016, 43(2): 25-33.]

[3] 贾洲侠, 吴振强, 吴建国, 等.飞行器气动热与结构传热双向耦合研究[J].强度与环境, 2019, 46(6): 16-23.[Jia Zhouxia, Wu Zhenqiang, Wu Jianguo, et al.Study on two-way coupled fluid-structure-thermal analysis for hypersonic vehicles[J].Structure & environment engineering, 2019, 46(6): 16-23.]

[4] Sarkar S, Atluri S N.Effects of multiple blade interaction on the containment of blade fragments during a rotor failure [J].Finite Elements in Analysis and Design, 1996, 23(2): 211-223.

[5] Xuan Haijun, Wu Rongren.Aeroengine turbine blade containment tests using high-speed rotor spin testing facility [J].Aerospace Science and Technology, 2006, 10(4):501-508.

[6] 谢文涛.航空发动机动力涡轮包容设计与验证技术研究[D].上海交通大学, 2017.

[7] 张晓峰.航空发动机机匣包容性的试验研究与仿真计算[D].浙江大学, 2005.

[8] Y F Deng, et al.Numerical study of failure modes and crack propagation in 2A12 Aluminum target against blunt-nosed pro-jectile at low yaw angle[J].Strength of Materials, 2016, 48( 6) : 834-849．

[9] 刘闯, 陈国栋, 黄福增,等.航空发动机机匣包容性试验研究[J].航空发动机, 2020,46(3): 71-76.[Liu Chuang, Chen Guodong, Huang Fuzeng, et al.Study on aeroengine casing containment test[J].Aeroengine, 2020,46(3): 71- 76.]

[10] Astrid K, Jorg F.Containment and penetration simulation in case of blade loss in a low pressure turbine[C].DYNA more LS-DYNA Forum, 2002.

[11] 赵武胜, 何先志, 陈卫忠, 等.盾构隧道地震相应分析方法及工程应用[J].岩土力学, 2012, 8: 2415-2421.[Zhao wusheng, He xianzhi, Chen weizhong, et al.Method for analyzing seismic response of shield tunnel and its application[J].Rock and soil mechanics, 2012,8: 2415-2421.]

[12] Xue L.Ductile fracture modeling-theory, experimental investigation and numerical verification [D].Massachusetts Institute of Technology, 2007.

[13] 孙力.动力涡轮叶片断裂转速分析方法研究[D].南京航空航天大学, 2018.

Simulation Analysis Research on Power Turbine-Casing Collision Failure of Micro-Turboprop Engine

LI Ji-yong LI Ying-xin MA Yang LI Fang HU Kai

(Sichuan Aerospace Zhongtian Power Equipment Co.,Ltd., Chengdu, 610100)

For the problem of blade cracks and casing’ containment during the hot-firing test of micro turboprop engine.The contact-impact dynamics method is used to simulate the crash failure process of the blade and the casing after a single blade is broken，in this way, analysis the collision location, energy change in the collision and the effective strain and stress.The results indicated that when a single turbine blade is broken，the tip and root of the blade will collide with the casing in turn, resulting in two impact points.Regardless of the influence of the remaining blades, the first impact point will dissipate part of the energy due to blade tip sliding, and the second impact point will be more impacted.Considering the motion of the circular turbine blade, the broken blades is influenced by the driving of the rear blade, which greatly improves the kinetic energy of the broken blade, makes the first impact point is more seriously impacted.In the case containment analysis, the effect of circumferential blade on the kinetic energy of fractured blade should be considered.

Turbine blade; Casing; Contact-Impact Dynamics; Containment

V432

A

1006-3919(2021)03-0046-07

10.19447/j.cnki.11-1773/v.2021.03.007

2021-02-04；

2021-03-28

李纪永（1985—），博士，高级工程师，研究方向：发动机强度、振动与可靠性；（610100）四川省成都市818信箱4分箱.