碳酸盐岩超声波速度频散实验研究

朱洪林, 陈 乔, 徐烽淋, 邓紫楠, 刘 洪,王 丹, 严灵芳, 陈春帆, 晏黎明

(1.重庆工商大学，重庆 400067； 2.中国科学院 重庆绿色智能技术研究院，重庆 400714；3.矿山地质灾害成灾机理与防控重点实验室，西安 710054；4.重庆涪陵页岩气环保研发与技术服务中心，重庆 涪陵 408102；5.重庆地质矿产研究院，重庆400042； 6.重庆四合燃气，重庆 涪陵408000；7.荆江水文水资源勘测局，湖北 荆州 434099)

速度频散与衰减是岩石物理领域一个前沿性问题，它不仅是开展频率域储层及流体预测的关键理论基础，同时也是解决不同地球物理测量方法(地震、VSP、测井、超声波岩心测试)之间数据匹配问题的重要手段。碳酸盐岩井壁稳定性分析中需要建立全井筒的岩石力学参数剖面，剖面的建立一方面需要测井资料，另一方面需要通过室内的静态三轴抗压实验和超声波透射实验来建立岩石力学参数预测模型[1]。但是目前井下测井频率一般在103～104Hz，而室内超声波透射实验用的超声波频率在105Hz以上，室内超声波频率远高于测井频率；因此，在不同频带的地球物理数据间联合应用时，实验室选用多大频率的探头完成岩石的超声波透射实验，用多大频率下的参数值来建立岩石力学参数预测模型显得至关重要。

有许多学者开展过岩石声波速度特性的相关研究[2-5]。M.Lebedev等[6]利用超声和成像技术得到了砂岩含水饱和度会引起速度变化现象的结论；M.L.Batzle等[7]利用超声测量技术和应力应变方法，研究了砂岩和碳酸盐岩流动性对速度的影响。在实验室测量中，岩石声学参数通常在超声频段下进行，此频段内起主要作用的频散或是衰减机制与地震频段下是不同的[8]。也有学者建立了多种理论模型来描述岩石的速度频散现象，如Squirt模型、BISQ模型、裂缝孔隙结构模型、双孔模型等[9-11]。滕佃波等[12]基于横波分裂理论，通过分离后的快、慢横波的振幅差异和时间延迟求取地下介质的裂缝走向方位和密度以及各向异性系数。T.B.Gregor等[13]的研究结果也表明，在碳酸盐岩地层中，当孔隙度一定时，随着地层中大孔隙的增加，其声波传播速度将逐渐增大并偏离Wyllie时间平均速度。孟庆山等[14]通过岩溶地区碳酸盐岩试样室内声波测试分析，发现纵、横波速与岩石的密度具有线性关系，利用密度、波速、纵横波速比或泊松比可初步判断碳酸盐岩在岩性上的差别，并且利用声波测试与岩石弹性模量之间的关系可以推算工程应用中所需的岩石力学参数。A.A.Saleh等[15]提出了一种更广泛的时间平均公式来描述声波速度与孔隙度之间的关系。刘财等[16]将岩石物理模型与传统遍历搜索方法和粒子群算法相结合，提出了基于粒子群算法的页岩孔隙纵横比反演以及横波速度预测的方法。此外，在复杂多孔介质波传播理论[17]、频散模型理论模拟[18]、流体黏滞性影响分析[19]、频散实验[20]等方面也开展了一系列研究，提出或发展了许多有价值的理论模型；但由于岩石本身的复杂性以及实验手段的限制，实验测量数据的可靠性和基于这些数据提出的各种理论模型适用性差别较大。

从上述资料可以看出，现有研究大都是在探究岩石流体类型、孔隙几何形状对声波速度的影响，很少考虑到速度随频率的变化，所建立的理论模型也重点集中在地震勘探领域，针对的是缝洞地层的地震识别与预测，而对超声波室内透射实验中不同频率带下，碳酸盐岩裂缝、孔洞对超声波速度的影响及应用研究仍然缺乏[21-24]。为此，本文以碳酸盐岩为对象，采用数值模拟与物理实验相结合的手段研究均质型、孔洞型碳酸盐岩的超声波速度频散特性。研究结果可为解决测井和室内超声波透射实验之间的数据匹配问题提供参考。

1 实验原理及过程

1.1 实验原理

1.1.1 物理实验原理

通过超声波透射实验进行波速等信息的获取，利用西南石油大学自主研发的多频率超声波测量仪进行测试，原理如图1所示。该装置由脉冲发生器、数字示波器、纵横波探头、微机及相应处理软件组成。采用透射法测量岩心的超声波响应，实验用换能器频率分别为纵波50、250、1 000 kHz，横波50、260、1 000 kHz。通过示波器采集透射波的波形，再提取首波速度进行波速计算(在本文中无论是物理实验还是数值模拟实验，均是提取首波速度进行波速计算，如图2所示)。

图1 多频率声波测量仪原理图Fig.1 Schematic diagram showing multifrequency acoustic wave measuring instrument

图2 超声波测量原理图Fig.2 The schematic diagram showing the ultrasonic measurementt1为入射波的一个起跳时间； t2为透射波的首波起跳时间； l为岩心长度; c为计算得到的首波速度

1.1.2 数值模拟原理

a.波动理论

用U表示某一时刻t二维空间上(x,y)任一点处的位移。二维声波方程如下

(1)

式中c(x,y)为纵波的传播速度。该方程的差分表达式为

(2)

在计算区域0≤x≤a和0≤x≤b内，取Δx=a/M，Δy=b/N，Δx和Δy分别为差分网格的水平距离和垂直距离；Δt为差分网格的时间；M和N分别为x方向和y方向的网格数的最大值。

令

αi,j=V(iΔx,jΔy)·Δt/Δx
βi,j=V(iΔx,jΔy)·Δt/Δy

(3)

这样二维声波波动方程的显式差分近似的离散化形式可表达为

(4)

b.波动方程有限差分求解

①初始条件

(5)

②边界条件

左右边界按常规反射边界处理，而上、下边界(y=0,y=b)则采用吸收边界条件

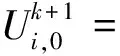
(6)

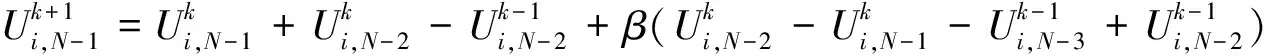
(7)

③振源条件

振源的初始条件为

(8)

④收敛性条件

(9)

实验室超声波测试是采用透射法进行测量。但由于岩心的非均质性及岩心内孔洞分布的不确定性，给研究孔洞对声学传播性质的影响造成了极大困难。而数值模拟则以被测岩样为模型，以实验室纵波探头的激发信号为输入振源，基于波动理论和有限差分方法用Matlab编程来实现超声波透射实验的模拟。本研究所采用的数值模拟方法有效性已在陈乔[25]的研究中进行了验证，即同频率同类型岩样数值模拟结果与物理实验获得的结果吻合较好，故此处不再赘述。

1.2 实验过程

选用25块碳酸盐岩进行实验研究，样品均取自川东北地区飞仙关组、长兴组的海相碳酸盐岩地层，岩心深度为4 697.36～6 125.69 m。将样品在实验室内加工成直径为25 mm、高为50 mm的圆柱体，两端用砂布磨平抛光以保证样品在进行超声波透射实验时能与声波探头良好耦合。25块样品中，有4块岩性为鲕粒溶孔云岩，孔隙度(q)、渗透率(K)范围分别为3.3%～24.3%、0.047 6×10-5～5.024 7×10-5μm2，平均值分别为16.375%、2.227 6×10-5μm2；其余样品均为鲕粒灰岩，孔隙度、渗透率范围分别为2.7%～8.9%、0.12×10-5～ 18.23×10-5μm2，平均值分别为3.7%、4.36×10-5μm2(图3)。

图3 岩心孔隙度、渗透率分布图Fig.3 The distribution of porosity and permeability of drilling cores

2 超声波速度频散特性数值模拟

2.1 均质碳酸盐岩超声波速度频散

考虑到均质型碳酸盐岩的理想性，本文利用超声波数值模拟的方法研究均质模型下多频率超声波的传播特性，岩心纵向剖面区域划分成50 mm×25 mm的模型，数字岩心骨架的波速(c)设置为 4 762 m/s，保持声波传播方向不变，计算所用频率(f)分别为50、100、200、300、400、500、600、800、1 000 kHz，探讨均质情况下不含孔隙时是否有频散现象发生。图4为波速与频率的相关性曲线的数值计算结果。

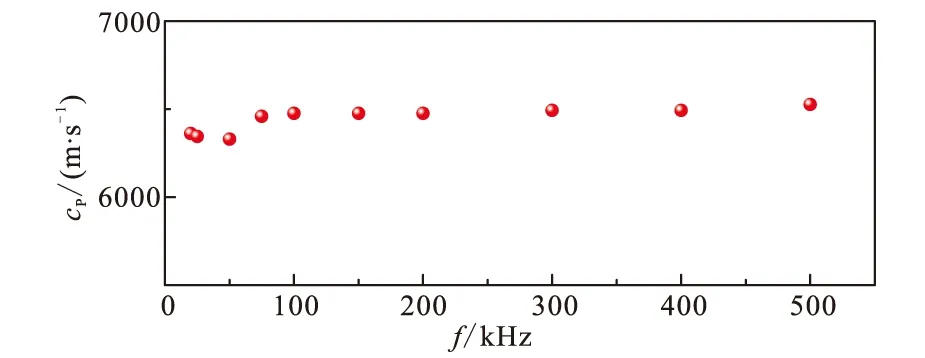
图4 均质情况下纵波速度与频率相关性Fig.4 The correlation of P-wave velocity and frequency under homogeneous condition

从均质模型多频率下的数值计算结果可以看出，当岩心为均质时，波速随频率的改变有微弱的波动并没有发生明显变化，最大与最小值之间仅相差8.8 m/s。因此，我们判定均质型碳酸盐岩并不存在频散现象。

2.2 孔洞碳酸盐岩超声波速度频散

通过超声波数值模拟发现均质碳酸盐岩本身不存在超声波频散现象，岩石出现频散可能是由于内部的孔洞结构引起的，而孔洞的大小、密度、分布状态是描述孔洞结构的显著特征。由于孔洞大小可用孔洞密度来表示，即孔洞越大，岩石含有的孔洞个数越少，孔洞密度就越小。因此，我们重点探讨岩石孔洞密度和分布状态对超声波传播的影响规律。

2.2.1 不同孔洞密度下超声波速度频散

我们利用数值模拟来实现岩石孔洞密度的变化：一是孔洞大小不变，通过增加孔洞数量来实现密度的调整；二是在总的孔隙度不变的条件下通过改变孔洞大小来调整密度。

a. 孔洞大小不变，增加孔洞数量

将本模型的孔径和孔深设置为相同大小，即横截面为正方形，边长均设置为0.6 mm，孔洞采用相同的分布方式，调整孔洞的数量分别为10、20、40、80、160、320个，对应的孔洞密度分别为800、1 600、3 200、6 400、12 800、25 600 m-2，从而实现孔洞密度变化。

数值模拟结果如图5—图7所示。图6为岩石纵波速度随孔洞密度的变化情况，可以看出在孔洞分布和大小相同的条件下，随着孔洞密度的增加，不同频率的纵波速度总体上均呈减小趋势(对数函数递减)，且曲线间出现整体“向下平移”的现象。在图中进一步给出了每个孔洞密度下岩石不同频率纵波速度的平均值、标准偏差和极差，结果发现随着孔洞密度的增加，平均声波速度减小，标准偏差和极差增大，说明孔洞的存在阻碍了声波传播，孔密度越大，平均速度就越小，也越容易引起速度频散现象。图7为不同孔洞密度岩石纵波速度随着频率变化情况，随着频率的增加，速度呈增大趋势(对数递增)，且曲线在250 kHz以后出现了较为明显的整体“向上平移”现象，而在250 kHz以下变化较为凌乱。同样在图中给出了每个频率下不同孔洞密度岩石纵波速度的平均值、标准偏差和极差，结果发现随着频率的增加，平均波速增加，标准偏差和极差减小，说明岩石孔洞密度本身也会引起声波速度的离散现象。但是随着频率越大，这种离散程度就越小，当频率为500 kHz时，标准偏差和极差显著减小，速度离散现象减弱；当频率达到 2 500 kHz时，速度极差为140 m/s，变化率仅为2%：也就是说当频率足够大时，离散现象会消失，可忽略孔洞的影响。

图5 频率为250 kHz时不同孔密度下的波场快照图Fig.5 Snapshot of the wave field at 250 kHz with different hole densities

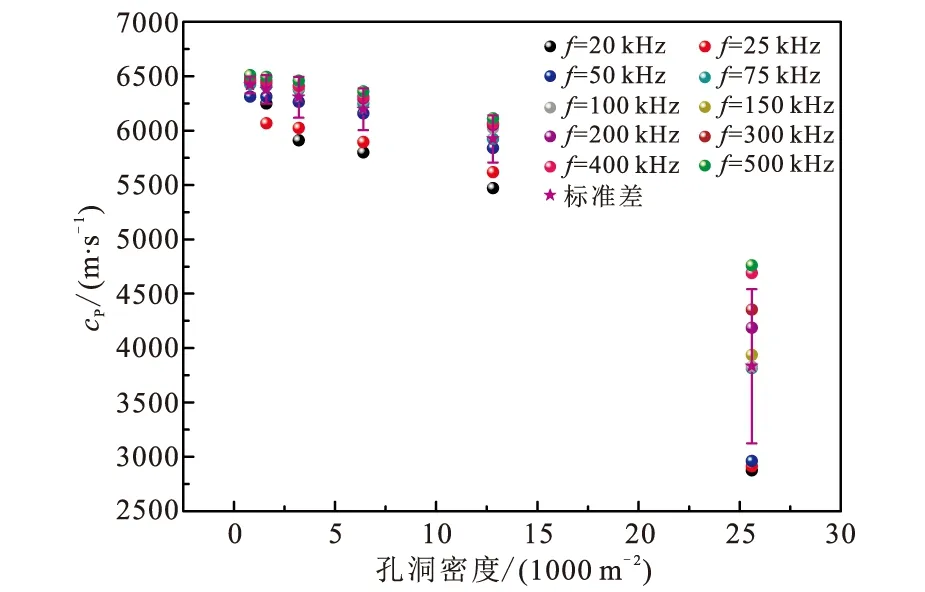
图6 不同孔密度(孔洞大小相同)的纵波速度Fig.6 The P-wave velocity with different hole densities (same hole size)

图7 不同频率(孔洞大小相同)的纵波速度Fig.7 The P-wave velocity with different frequency (same hole size)

将模型孔洞形状设为圆形，在孔隙大小(孔隙度)不变的情况下，通过改变孔洞的半径来实现孔洞数目的改变，半径分别设置为2、1.4、1、0.8 mm，孔洞数量分别为10、20、40、60个，对应孔洞密度分别为640、1 280、2 560、3 840 m-2。

数值模拟结果如图9、图10所示。由图9可以看出在孔洞分布相同的条件下，随着孔洞密度的增加，纵波速度先增加后减小。这是由于开始阶段岩样的孔洞数量虽然增加了一倍，但是孔洞半径减小了30%，单个孔洞对声波的阻碍作用减弱，使得孔洞数量对声波速度的削弱值小于孔洞半径减小引起的速度增加值；而在孔洞半径减小到一定程度后，孔洞大小不再是影响波速的主要因素，波速随着孔洞数量增加呈线性递减，而且随着孔洞密度的增加，声波速度的极大值和标准偏差都呈增大趋势，速度频散现象增大，说明岩心的孔洞结构会引起速度频散现象。图10给出的是纵波速度与频率的关系曲线，速度随着频率的增加整体呈递增趋势，而标准偏差与极差值随频率的变化规律杂乱，<500 kHz的频率时，标准偏差和极差呈先减小后增大趋势。对比发现标准偏差和极差的减小是由于半径最大的孔洞岩石的声波速度突然降低造成的，如果除去该点后，标准偏差几乎不变，速度离散现象减弱，这也验证了频率越高的声波越不容易发生速度离散现象。

图8 频率为250 kHz时不同孔密度下的波场快照图Fig.8 Snapshot of the wave field at 250 kHz with different hole densities

图9 不同孔密度(孔隙度不变)的纵波速度Fig.9 The P-wave velocity with different pore densities (same porosity)

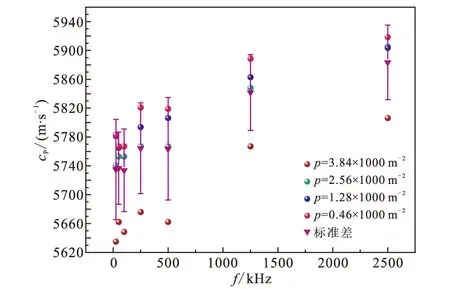
图10 不同频率(孔隙度不变)的纵波速度Fig.10 The P-wave velocity with different frequency (same porosity)

2.2.2 不同孔分布下超声波速度频散

本节通过人造孔洞来研究孔洞分布对超声波的影响。多孔分布对波速的影响研究所用到的模型为A1 、A2、 A3、 A4、 A5，这5种模型的孔洞数量均为6个，孔径均为1.6 mm，孔深均为6 mm(图11)。

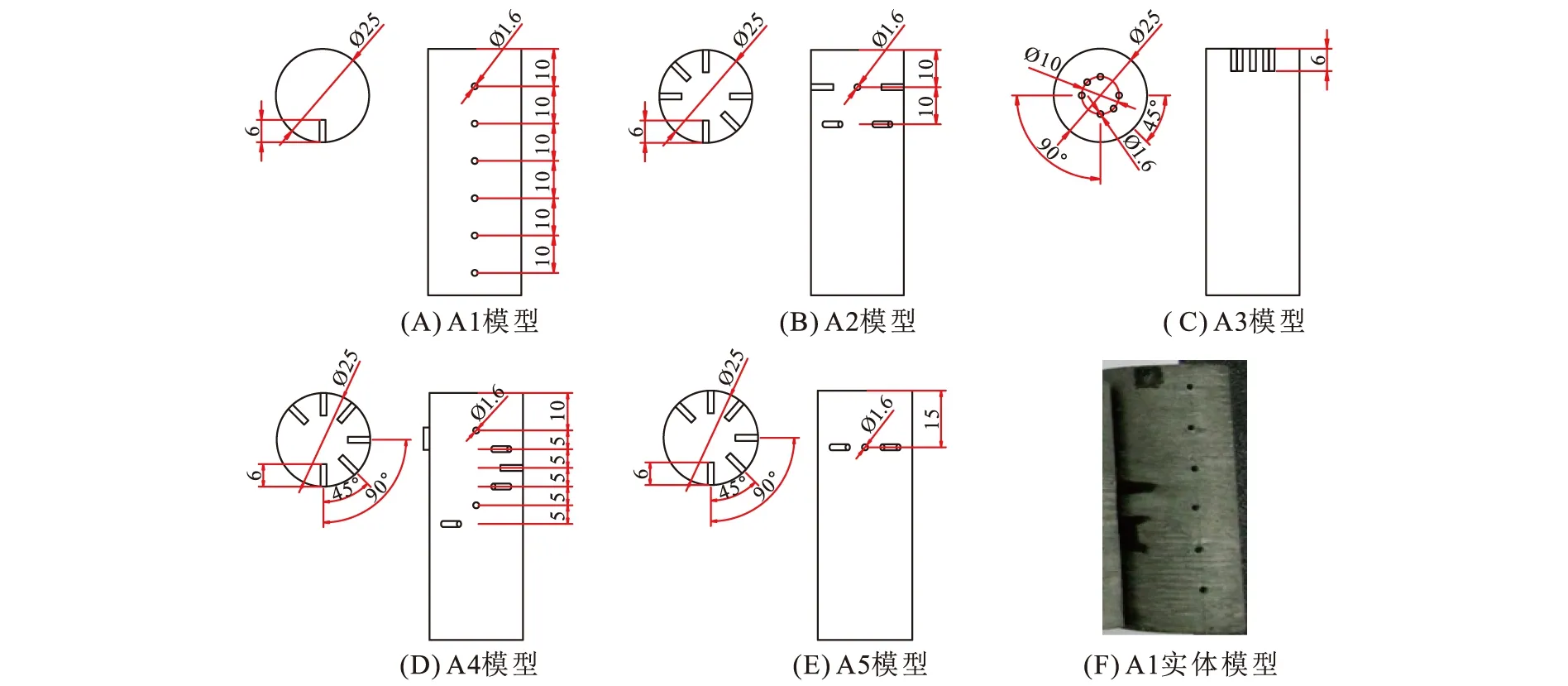
图11 不同孔洞分布模型Fig.11 The models of different hole distribution

不同模型在多频率下的声波速度及不同大小下的声波速度如图12、图13所示。

物理实验的结果表明：多孔洞分布情况下，随着频率的增加，纵波速度呈增加的趋势，频散较为严重；随着孔洞分布的变化，速度发生了变化，分布4和分布5即模型A4和A5情况下波速减小。从模型图不难看出在这两种模型下孔洞在岩心横截面上分布得最均匀，阻碍声波传播的面积也越大，而且孔洞分布状态会引起速度频散现象。横波随孔洞分布和频率变化没有体现出规律性较强的变化(图12-B)。从图13可以看出，同一频率下孔洞分布变化的速度标准偏差较小，速度离散程度低，说明该孔洞分布没有影响到声波传播的最短路径。

图12 孔洞分布变化对纵横波速度的影响Fig.12 The influence of pore distribution variation on longitudinal and transverse wave velocity

2.3 碳酸盐岩样品大小对超声波频散的影响

为了能更好地了解测井声波在井下地层中的传播特性和岩石的声学参数，在实验室对岩石样品进行超声波测试。由于受岩心样品来源、取样条件和测试方法等实验室条件的限制，被测样品形态通常被加工成小直径的圆柱体，使得岩石样品超声波速度测试是在有限尺度样品上进行。

对于孔洞型碳酸盐岩地层，当含有孔洞时会引起频散。由于纵波作为一种压缩波，传播方向与质点震动方向相同，传播过程与纵向距离有关系而与横向尺寸关系不大，因此频散的出现是否与岩心长度有关或者受岩心长度的影响未知。因此，本文讨论当孔洞发育时，对于柱塞型岩样其频散现象是否与岩心长度有关。

作者设计了含孔洞的非均质模型进行研究。表1是含孔洞数字岩心模型的参数(孔隙度为16%)，在上述基础上进行数值计算。数值计算用的纵波频率分别为50、100、200、300、400、500、600、800、1 000 kHz。数值计算结果见图14、图15。

表1 含孔洞数字岩心模型的参数Table 1 The parameters of digital core model with holes

图14 不同长度岩心的纵波速度与频率的关系Fig.14 The relationship between longitudinal wave velocity and frequency under different length of cores

图15 不同频率时岩心纵波速度与长度的关系Fig.15 The relationship between longitudinal wave velocity and specimen length under different frequency

图14为不同岩心长度下纵波速度与频率的关系图，如图中红色包络曲线所示，当频率低于200 kHz时波速随频率变化极小，长度变化几乎不会引起速度的离散；如图中绿色包络曲线所示，当频率大于300 kHz时波速随频率增大而变大，也未出现较明显的速度离散现象。图15为岩心纵波速度与长度的关系图，可见随着岩心长度的增加，平均波速基本保持不变，而相同长度、不同频率岩石的声波速度较为离散，也就是说不同长度的岩心也存在频散现象，只是这种频散现象并没有随岩心长度的变化发生改变。

3 结 论

a.在碳酸盐岩储层中，因频率不同而呈现的速度频散及衰减现象是客观存在的，且整体上呈现出速度随频率的增加而增大的特征，但不同频带范围内变化特征不同。

b.通过数值模拟发现，均质型碳酸盐岩不存在速度频散现象。孔洞型碳酸盐岩存在明显的速度频散现象，随着孔洞密度的增大，速度频散程度越高，而且孔洞结构本身会导致波速发生离散，这种离散随着频率的增加而减小；不同孔洞分布特征、长度的碳酸盐岩样品也会出现速度频散，但是它们本身几乎不会导致速度发生离散。这说明碳酸盐岩内部的孔洞结构极易改变声波在岩石中传播的最短路径，而人造孔洞的分布特征、长度并没有引起最短路径的改变。

c.深入研究速度频散的基本规律及其影响因素，明确频率与速度的相互关系，将为从本质上解决不同地球物理测量方式间的数据匹配问题奠定基础。该问题解决的现实意义，即能够实现将千赫兹级的测井速度在合理校正到几十赫兹的地震频带之后再用于井震标定及后续的反演工作，从而在本质上弥补当前井震标定过程因频散效应的存在而造成的理论缺陷，进而为提高储层预测的精准度奠定基础。尽管如此，由于岩石声波速度频散的影响因素很多、也很复杂，作者的研究工作目前考虑的只是其中很小的一部分，诸如孔隙流体介质、孔洞形状及组合、测试环境条件等等还没有考虑，所以结果的适用性尚存在一定的局限性，扩展至低频段的模型及相关实验技术还有待进一步深入探究。