井下超宽带人员定位的改进卡尔曼滤波算法

刘永立， 吴闻轩

(黑龙江科技大学 矿业工程学院， 哈尔滨 150022)

0 引 言

超宽带与短距通信技术相比拥有定位精度高、穿透性强，以及抗多径干扰能力强、功耗低等特点[1-2]，因此，更适用于井下人员定位。但在定位过程中，由于煤矿井下复杂环境，导致超宽带通过无线传输数据时，受采煤机械发出的电磁波及来自其他设备的噪声干扰[3-4]，导致测距值偏移，定位精度波动大，因此，如何减小噪声带来的干扰，成为了超宽带定位技术应用于煤矿的关键。

郭继坤等[5]提出了奇异点带内滤波技术应用于UWB通信，通过分析小波奇异性模极大值衰减速度描述UWB的奇异性，仿真实验验证了该技术有利于提升信噪比。谭玉新等[6]通过无损卡尔曼滤波技术(UFK)对井下机器人进行定位，运用UFK对机器人的坐标及航向角度进行滤波，得出该方法优于光电码盘定位的结论。邢智鹏等[7]提出LQI滤波和RSSI结合的定位算法，通过LQI指标的滤波性能对数据进行滤波提高抗干扰性，最终通过紫峰硬件平台验证该算法的有效性及优势。

笔者基于卡尔曼滤波可消除噪声的基础上，结合卡尔曼滤波与超宽带TWR算法，提出卡尔曼滤波改进算法，对测距数据进行滤波处理，分离测距数据与误差，以使两者互不干涉。

1 超宽带及定位原理

1.1 超宽带

超宽带(Ultra-wide band，UWB)是一种可以给无线局域网WLAN和个人局域网PAN带来低功耗、大带宽并且能进行短距离无线通讯的无线通信技术，与现在的主流的4G通信方式不同之处在于超宽带可以进行无载波通信[8]，其数据传输可以仅通过非正弦波的窄脉冲进行传输。与其他短距通信技术相比，超宽带拥有定位精度高、穿透性强、抗多径干扰能力强、功耗低及传输距离远[9]等特点，使超宽带技术更适用于煤矿井下人员定位。

由于井下工作环境复杂，大型机械设备的噪音、电磁波等对人员定位技术干扰大，故亟需改进人员定位算法，提高井下人员定位技术的精度和抗干扰能力。

1.2 超宽带三边定位算法

为减弱采场地应力变化对晶振时钟的影响，选择三边定位算法提高定位精度[10]，原理如图1所示。以基站本体为中心，半径50～600 m的圆形范围内对标签信号进行捕捉，上位机根据基站接收的测距值d0、d1、d2进行定位。

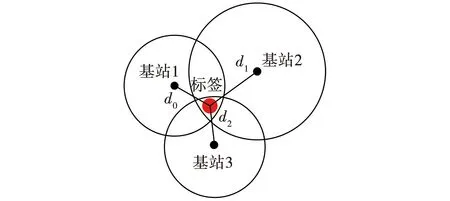
图1 三边定位算法原理Fig. 1 Trilateral positioning principle

定位源于测距，基于TOA的TWR测距算法在煤矿井下因电磁干扰混入噪声信号时易产生数据错位，导致定位精确度下降，因此,采用TWR改进算法。

1.3 TWR改进算法

TWR改进算法[11]原理如图2所示。

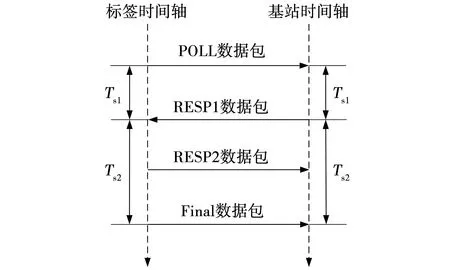
图2 超宽带TWR改进算法Fig. 2 Improved UWB TWR algorithm

相较于传统TWR算法，增加了RESP数据包，用于确保数据包在信息传递过程中不会发生错位现象，根据标签与基站传输的时间差确定测距值为

(1)

式中:c——光速;

Tr——测距周期;

Ts——标签回复时间用于确认数据包编号。

井下人员定位时，标签发出的信号会混入白噪音，基站接受的信号会捕捉到机械设备发出的电磁波，这些都会降低定位的精度。式(1)仅考虑了数据交互的准确性，未考虑在数据传输过程中的噪声和电磁波干扰，测距误差在0.5 m左右。因此，需要加入一种能够滤除噪声和电磁波干扰的算法，减少测距数据偏移，提高定位精度。

2 井下人员定位算法

2.1 卡尔曼滤波算法原理

卡尔曼(Kalman)滤波算法是基于状态空间的递推滤波算法[12]，如图3所示。其算法主要针对状态空间和测量空间，前者通过状态方程描述相近时段状态转移变化规律，后者反映观测值与状态值之间的关系。

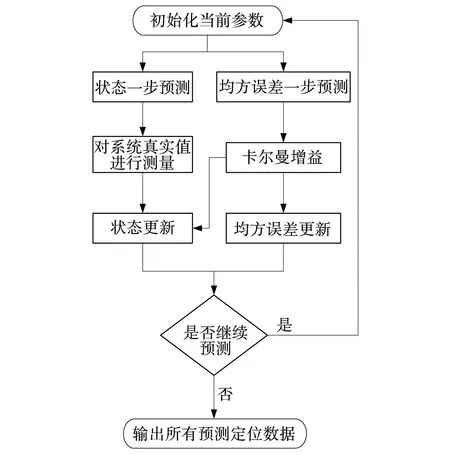
图3 卡尔曼滤波流程Fig. 3 Flow of Kalman filter

初始状态和均方差的一步预测：

X(K)=φKX(K-1) ，

(2)

式中:X(K)——K时刻系统真实状态矩阵；

φK——状态转移矩阵，包含位移、速度和加速度等关系式；

DX(K,K-1)——系统协方差矩阵。

系统真实值Z(K)的测量为

Z(K)=HkX(K)+V(K)，

式中:HK——m×n阶矩阵，表示X(K)对测量变量Z(K)的增益；

V(K)——期望值为0的观测噪声。

卡尔曼收益为

式中，RK——观测噪声V(K)的协方差矩阵。

将收益代入状态更新及均方差更新公式中，更新当前状态

X(K,K)=X(K,K-1)+KK[ZK-HKX(K,K-1)]，

DX(K,K)=(I-KK×HK)DK(K,K-1)，

式中，I——单位矩阵。

对超宽带井下人员定位信号的滤波问题在于卡尔曼滤波算法和TWR改进算法结合时，如何降低测距数据中的系统噪声和白噪声，结合测距数据及状态转移规律来得到定位的最优估计结果。

2.2 卡尔曼滤波改进算法

采用递归方法将卡尔曼滤波算法与TWR算法相结合，能够有效解决噪音和电磁波干扰。根据测距数据及状态转移规律，使用当前测距值以及前一个测距周期即可进行估值计算，得到定位的最优估计结果。流程如图4所示。

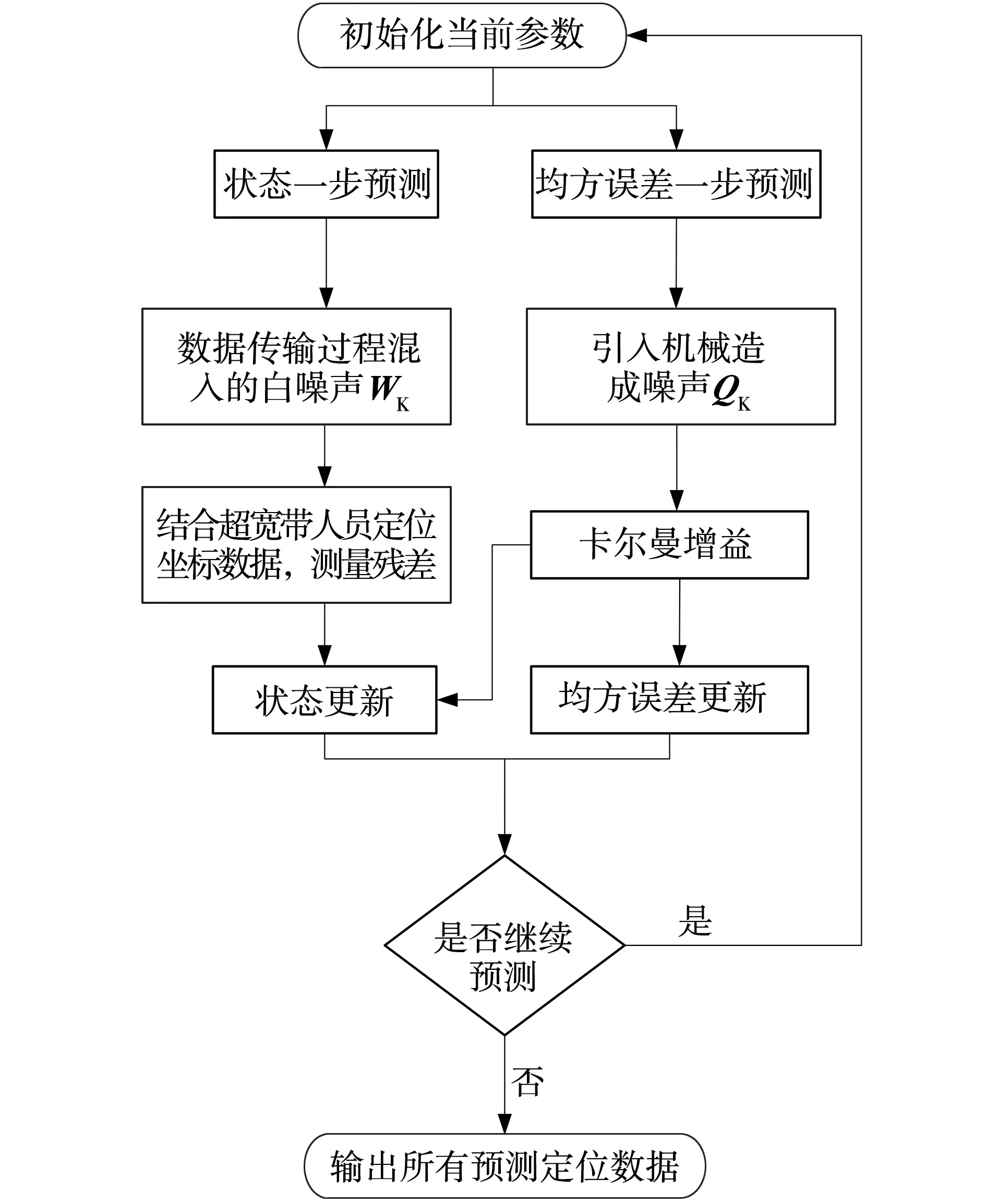
图4 卡尔曼滤波改进算法流程Fig. 4 Improved flow with Kalman filter combined with UWB downhole positioning

使用随机线性微分方程，用于预测当前状态X(K,K-1)，根据系统状态变量K-1时刻的最优值和系统输入计算出K时刻的状态预测值为

X(K,K-1)=φKX(K-1,K-1)+BKUK+WK，

(3)

式中:φK——在X(K,K-1)状态下的变换矩阵，是井下人员定位算法对于状态变量进行预测的基础；

BK——系统参数；

UK——K时刻对系统的控制增益或者控制量；

WK——白噪声，当X(K)为一维定位数据时，WK=1，UK不存在。

协方差方程用于时间预测为

(4)

式中,QK——系统噪声的协方差，即系统误差。

将QK纳入时间预测可以使其在不断向前预测的过程中迅速收敛。

利用式(4)的所得结果，代入卡尔曼增益方程，计算卡尔曼收益

(5)

式中,HK——标签的预测矩阵，当DX(K)为一维矩阵时HK=1。

更新最优值方程时，结合卡尔曼滤波的测量方程与TWR改进算法，计算出K时刻状态变量的最优值为

X(K,K)=X(K,K-1)+KK[rho(K)-

(6)

式中:rho(k)——曲线饱满值，用于滤除超宽带信号测距传输过程中混入的噪声，减少数据抖动使得定位曲线平滑，使用当前坐标对X(K)的状态方程进行更新;

Δt——测距间隔周期值。

由式(4)、(5)可以推算更新协方差方程，得出K时刻的协方差矩阵DX(K,K)，同时为得出K+1时刻的输出值做铺垫

DX(K,K)=(I-KKHK)×DK(K,K-1)。

(7)

利用K时刻测距值对K+1时刻继续进行时间预测和测量更新，重复式(3)～(7)的计算过程，直到测距结束完成对井下人员定位数据的滤波过程。

卡尔曼滤波改进算法是根据当前基站的测距值、上一时刻预测的测距值及误差，计算得出当前最优值，再进入下一个预测循环中。该算法使混入的噪声及电磁波产生的误差独立存在，降低误差干扰。

3 仿真与实际测试

3.1 仿真实验

为了验证经卡尔曼滤波算法改进后的超宽带煤矿井下人员定位系统的定位精度、可靠性及输出数据是否稳定，使用Matlab进行仿真，仿真环境设置如图5所示，长度为30 m，宽度为3 m长方形区域，设定采煤工作面生产过程中，采煤设备噪声达到90 dB，巷道内电缆符合MT818-2009规定，极少出现打火现象；T0到T2为三个基站，仿真设置由人员佩戴标签在该范围内从T0处出发沿规划路线行走，数据扫描周期为5 ms共扫描30次。

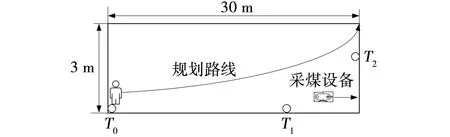
图5 仿真环境设置示意Fig. 5 Schematic of simulation environment setting

将卡尔曼滤波算法改进前后超宽带定位路线与规划路线进行比对，横坐标d为巷道宽度，纵坐标l为巷道长度，如图6所示。对图6c卡尔曼滤波改进前后两组路线数据进行位置偏移值拟合，如图7所示。

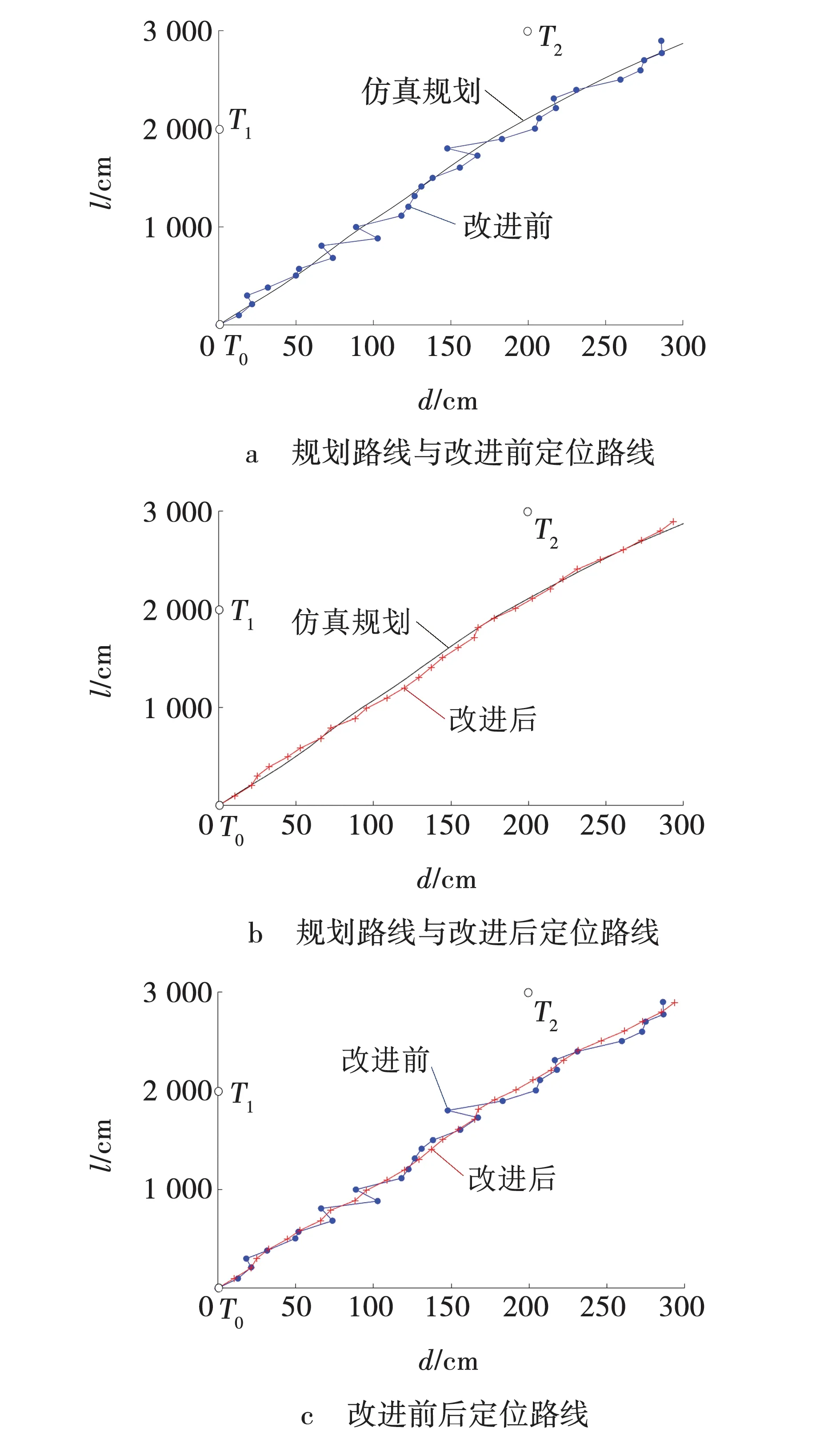
图6 卡尔曼滤波算法改进前后与仿真规划路线比对Fig. 6 Kalman filter algorithm was compared with simulation planning route before and after improvement

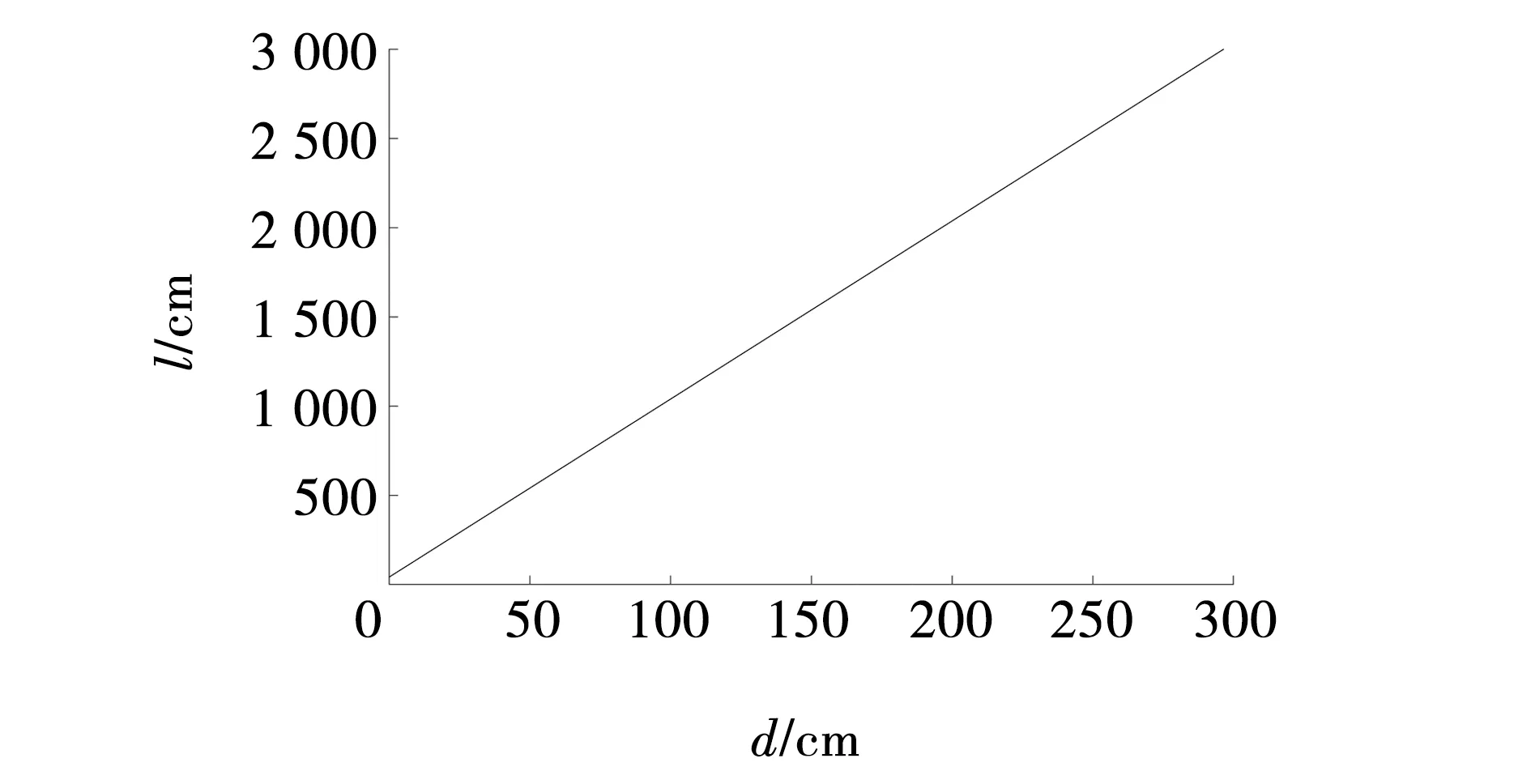
图7 卡尔曼滤波算法改进前后定位偏移值拟合函数Fig. 7 Kalman filter function turns on front and rear positioning offset fitting function

由仿真结果可知，卡尔曼滤波算法改进前定位数据受到干扰，导致给出的定位路线与设定的行动路线偏差较大，而卡尔曼滤波算法改进后，定位路线更加接近于规划路线。由拟合函数表达式y=9.98x+41.262可知，斜率越大说明卡尔曼滤波改进算法对于定位数据的降噪性越强。

3.2 实际测试

为了验证卡尔曼滤波改进算法能使超宽带井下人员定位系统在煤矿井下传输的数据更平稳，定位更精确，依托黑龙江科技大学地下模拟矿井,现场实测如图8所示。

图8 现场实测Fig. 8 Field test

测试环境设置为综采工作面起始点至直线长度为30 m的范围内，采煤机噪音等级达到97 dB，使用单个基站和标签，每3 m设置一个记录点，记录10次使用卡尔曼滤波前后标签与基站间的测距误差数据，实测方案示意如图9所示。

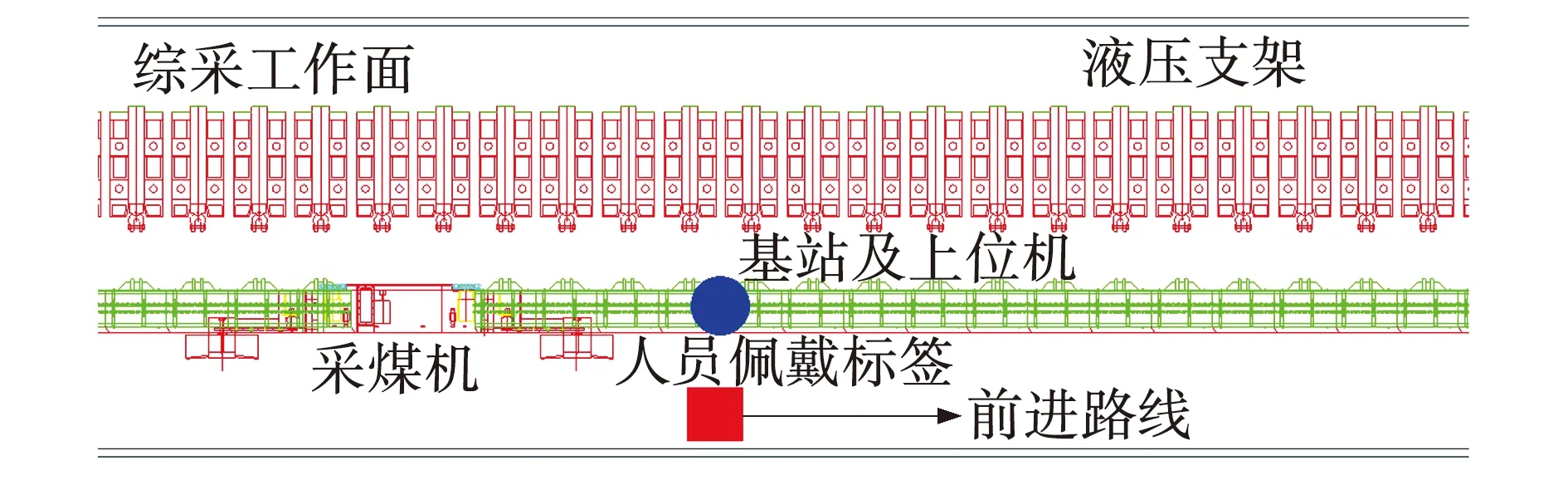
图9 实测方案示意Fig. 9 Schematic of measured scheme

测距结果如表1所示。其中，ds为实际值，使用钢卷尺测量，dq为卡尔曼滤波改进前测距值，dh为卡尔曼滤波改进后测距值。

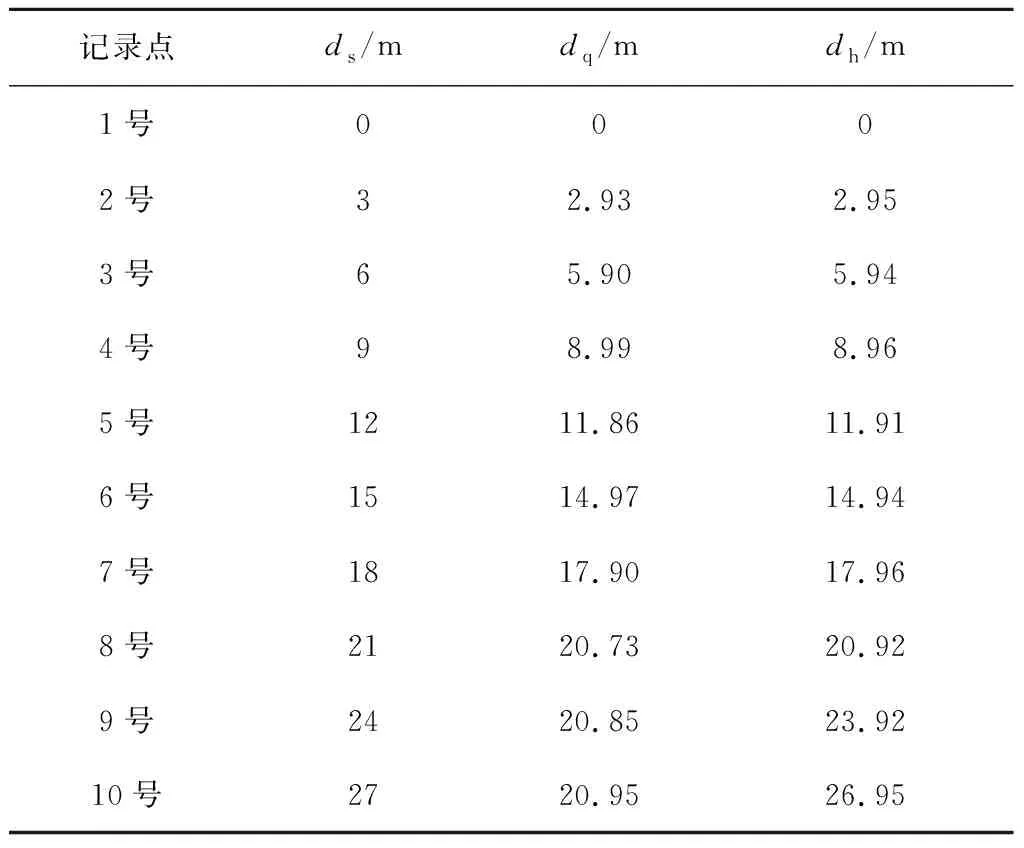
表1 卡尔曼滤波改进前后测距值

将表1测距数据导入Matlab进行误差处理分析，所得结果如图10所示,其中，横坐标n表示记录点，纵坐标e表示误差值。在卡尔曼滤波改进算法对测距数据进行处理前，测距误差波动极大且不稳定，而卡尔曼滤波算法改进后，测距误差下降，且由于卡尔曼滤波具有向前预测性，使误差逐渐趋向于0，数据更精确。

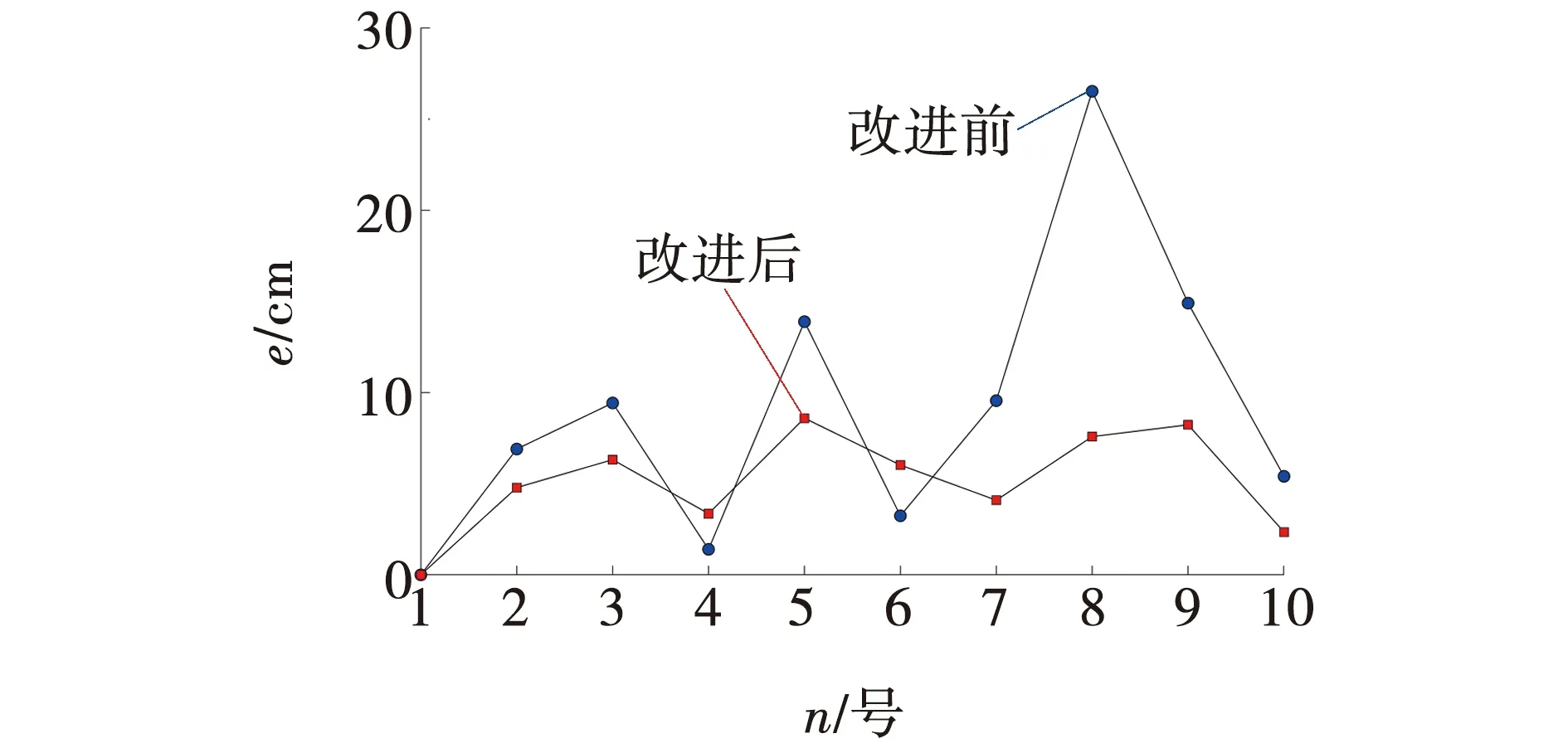
图10 卡尔曼滤波前后测距误差对比Fig. 10 Comparison of ranging errors before and after Kalman filtering

卡尔曼滤波算法改进前后测距残差如图11所示，其中纵坐标s表示残差值。利用残差图判别随机误差，反复修正卡尔曼系统参数，在残差图结果趋于理想化的同时，使卡尔曼滤波算法与TWR改进算法结合性进一步提高。

图11 卡尔曼滤波算法改进前后测距残差Fig. 11 Range residuals before and after Kalman filtering

结果表明，总体误差基本控制在0～10 cm范围内，误差范围相较于单一的TWR改进算法10～50 cm范围有更大的提升。

4 结 论

为解决井下人员定位系统在运行过程中存在的测距误差波动幅度较大，定位输出数据不够稳定，导致定位精度不足的问题，提出了将卡尔曼滤波算法与超宽带定位算法相结合，对各基站测距数据进行了卡尔曼滤波处理。

(1) 卡尔曼滤波改进算法使定位轨迹与实际路线相吻合，误差范围控制在0～30 cm，定位精度较卡尔曼滤波算法未改进时有较大提升。

(2)卡尔曼滤波改进算法使测距误差降低至10 cm范围，较原算法0.5 m误差有较大提升符合矿井人员定位系统的安全要求规定。