CVIS混合供电路侧单元的时延-功耗优化调度策略

时 颖

(1.黑龙江科技大学 电子与信息工程学院， 哈尔滨 150022； 2.哈尔滨工程大学 信息与通信工程学院， 哈尔滨 150001)

0 引 言

车路协同(Cooperative vehicle infrastructure system，CVIS)是自动驾驶的必由之路[1]。沿路两侧设置路侧单元(Roadside unit，RSU)，作为行驶车辆提供信息服务的网联接入设备，同时也作为环境监测传感器网络节点，承担着监测数据的传输任务。但在边远山区、荒漠戈壁等地区，RSU无法实现与电网和互联网连接[2]。随着对绿色通信的新需求，RSU配备可通过太阳能和风能等可再生能源进行自供电[3]。然而可再生能源的能量收割受外界环境因素影响较大，会有长时间无法收集到能量的情况，这势必将影响“车-路”间的数据传输，甚至会影响车辆的安全行驶。为避免出现上述问题，可考虑给RSU附加备用电池，形成混合供电模式。由于地理位置的限制，备用电池更换周期长，为了兼顾备用电池的使用寿命及车路协同的低时延特性，有必要研究时延-功耗的折中优化问题。时延-功耗折中优化的研究难点之一是通信系统数据到达的随机性。B. Collins[4]利用跨层法给出了时变信道下具有时延约束的传输调度策略。R. A. Berry等[5-6]指出了衰落信道中的功率-延迟折中问题，考虑能量收割的随机性，在保证传输质量的同时，充分利用收割能量是另一个难点。O. Orhan等[7]研究了在已知收割能量和功耗约束的条件下，使数据传输最大化的最优传输策略。R. Atallah等[8]进一步考虑时变信道，分析如何获得系统吞吐量的最大化。J. Liu等[9]同时考虑数据和能量到达的随机性，利用跨层法研究了时延最小化调度策略问题。

笔者充分考虑车路协同的实际通信场景，引入RSU覆盖范围内车辆到达、数据和收割能量到达的随机性，提出基于概率参数的联合调度系统模型，以联合系统状态转移建立二维Markov链，利用排队论构建有约束的RSU平均时延最小的优化目标函数，求解出最优稳态概率，获得具有门限结构的优化调度策略。

1 系统模型

文中所研究的RSU间数据传输场景主要包括两个部分：其一，由于地理位置的限制，RSU无法接入电力系统和互联网，从绿色通信和保证车路协同系统通信稳定两个角度出发，考虑采用混合供电方式；其二，RSU与进入其覆盖区域内车辆进行数据传输，传递环境监测数据和其他服务信息。场景中RSU收集到的环境监测信息和其他服务信息以数据包的形式到达MAC层后存储在缓冲区队列中，用于数据传输消耗的功率由两种能源提供，即从环境中获取的可再生能源，以及有一定使用寿命的可供能源。考虑到收割能量的不稳定性和车辆到达的随机性，RSU发送端中调度器采用调度传输策略以实现最小的平均排队时延。

1.1 数据和能量队列模型

联合调度模型如图1所示。系统模型采用动态数据包的到达模型来模拟RSU数据和从外围环境收割到能量的到达过程。假设数据包到达服从伯努利过程，速率为η1∈[0,1]，每个到达数据包含k1个数据包。设a1[t]表示第t时隙开始时RSU中到达的数据包数，其概率质量函数可表示为

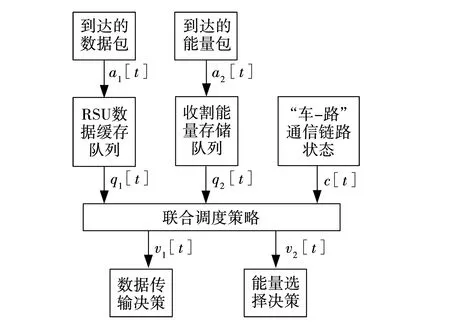
图1 联合调度模型Fig. 1 Joint scheduling model

Pr{a1[t]=k1}=η1,

Pr{a1[t]=0}=1-η1。

RSU数据缓冲区队列的容量设为Q1，q1[t]表示第t时隙末数据队列长度，则此队列的更新状态为

q1[t]=min{q1[t-1]+a1[t],Q1}-v1[t]，

(1)

式中，v1[t]——在第t时隙决策要传输的数据包数。

具有能量收割功能的RSU能够从环境中获取能量，收割来的能量可用于传输数据，无需使用备用电池供电。由于环境变化的随机性，有可能会发生长时间无法收集到能量的情况，这势必会影响到RSU中监测数据的传输，增大数据传输时延，因此，RSU数据传输不能完全依赖于能量收割。

假设能量按照一定分布概率随机到达队列，当使用该收割能量来传输RSU数据时，一定数量的能量包离开队列，因此，收割能量的储存和消耗过程可以描述为一个排队系统。对于用来存储收割能量的电池容量也存在上限，设为Q2，这意味着该电池最多只能储存Q2个能量包。q2[t]表示第t时隙末收割能量的队列长度，即电池剩余能量包数。用a2[t]来描述能量收割的到达过程，表示每个时隙内收获的能量包数，k2个能量包以概率η2到达队列。因此，a2[t]的概率质量函数为

Pr{a2[t]=k2}=η2，

Pr{a2[t]=0}=1-η2。

相似地，能量队列的更新状态为

q2[t]=min{q2[t-1]+a2[t],Q2}-v2[t]，

(2)

式中，v2[t]——在第t时隙中消耗的能量包数。

所有数据包需通过RSU与车辆的通信链路中继转发到目标RSU或其他车辆，但由于车辆到达RSU覆盖范围内的时间是不确定的，具有随机性，因此“车-路”通信链路状态可以使用“空”和“忙”两个状态来描述。为方便分析，设c[t]表示第t时隙时“车-路”通信链路状态，c[t]=1表示链路已连接，信道状态为“空”，可以传输数据；c[t]=0表示链路未连接，信道状态为“忙”，不可以传输数据。链路状态的质量分布函数为

Pr{c[t]=1}=α，

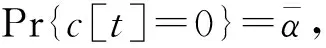
式中，α——在每个时隙中链路状态保持“空”的概率。

当链路状态为“空”时，RSU应该向链接车辆成功传送数据包，由收割能量队列的能量包或由备用电池提供能量。通常，联合调度器更倾向于使用收割来的能量包，因为这样做可以延长备用电池的使用寿命，且它是可再生的。然而，由于能量收割的不确定性，可能需要等待很长时间来获取仅能用于一次数据传输的足够功率，这对于时延敏感的智能交通控制是不可容忍的，此刻应采用备用电池供电。然而，如果发射机过于依赖备用电池的可靠能源供电，极大影响备用电池的使用寿命，直接影响交通控制效果。因此，在排队时延和从可靠能源备用电池中获取的传输功率之间存在折中关系。

1.2 调度策略

文中提出的RSU数据传输概率调度策略，包括数据队列状态、收割能量队列状态及“车-路”通信链路状态三个决定性因素，寻找最优调度参数来获得在消耗可靠能源功率约束下的最小平均排队时延。调度中心采用的概率调度策略，即在每个时隙开始，根据到达状态a[t]=(a1[t],a2[t])、“车-路”通信链路状态c[t]，以及上一个时隙末的队列状态q[t-1]=(q1[t-1],q2[t-1])，决定当前时隙是否进行数据传输，若传输应采取多大的传输概率进行调度策略。设gi∈[0,1]和fi∈[0,1]分别为当前时隙有、无数据到达情况下的传输概率；反之，1-gi和1-fi分别为当前时隙有、无数据到达情况下的继续等待概率。为便于分析，排队系统在第t时隙的系统状态变量表示为s[t]=(a1[t],a2[t],c[t])，动作变量表示为v[t]=(v1[t],v2[t])。文中分四种情况建立概率调度策略的数学参数化表达式。

情况1数据队列非空，而收割能量队列为空，即

q[t-1]=(i,0) (i>0)，

其中，符号‘w’是‘with probability of ’的简写，表示“以概率”；符号“·”表示任意值。当“车-路”通信链路建立成功(c[t]=1)时，不论是否有新的数据到达，只要收集到能量包(a2[t]=k2)，就会消耗一个能量包(v2[t]=1)来传输一个数据包(v1[t]=1)。然而，如果没有新到达能量包(a2[t]=0)，此时若有新的数据到达(a1[t]=k1)，调度中心则以概率为gi的调度策略选择消耗备用电池能量发送一个数据包，或者以1-gi概率继续等待；如若没有新的数据到达(a1[t]=0)，调度中心则依概率为fi的调度策略选择消耗备用电池能量来发送一个数据包，或者以1-fi概率继续等待。

情况2数据和收割能量队列均非空，即

q[t-1]=(i,j),(i>0,j>0)，

不管数据和能量到达状态如何，只要“车-路”通信链路建立成功，都会消耗一个能量包用于传输一个数据包。

情况3数据队列为空，而收割能量队列非空，即

q[t-1]=(0,j),(j>0)，

此情况下，有足够的收割能量储存在电池中，只要通信链路建立并有新的到达数据，即以1的概率传输一个新的到达数据包。

情况4数据和收割能量队列均为空，即

q[t-1]=(0,0)，

在第t时隙内，当新的数据和收割能量都到达时，数据将利用收割能量来传输。若仅有新的数据到达，调度中心则以g0概率选择备用电池能量来传输数据，反之，以1-g0的概率继续等待。上述情况，仅在“车-路”通信链路建立时发生。

1.3 二维Markov链模型

依据概率调度策略分析，RSU传输决策是基于时隙中的队列状态q[t-1]和系统状态s[t]做出的。因此，该排队系统可以用q[t]作为转移状态，以Pr{q[t]|q[t-1]}作为状态转移概率的二维Markov链进行描述。为了便于标注和简化转移概率符号表示形式，首先定义以下4个参数：

通过分析4种概率调度策略，可以发现调度策略仅在无收割能量可用时来决策以某概率进行传输或等待。因此，状态{(i,0)|i>0}之间的状态转移概率可以定义为

(3)

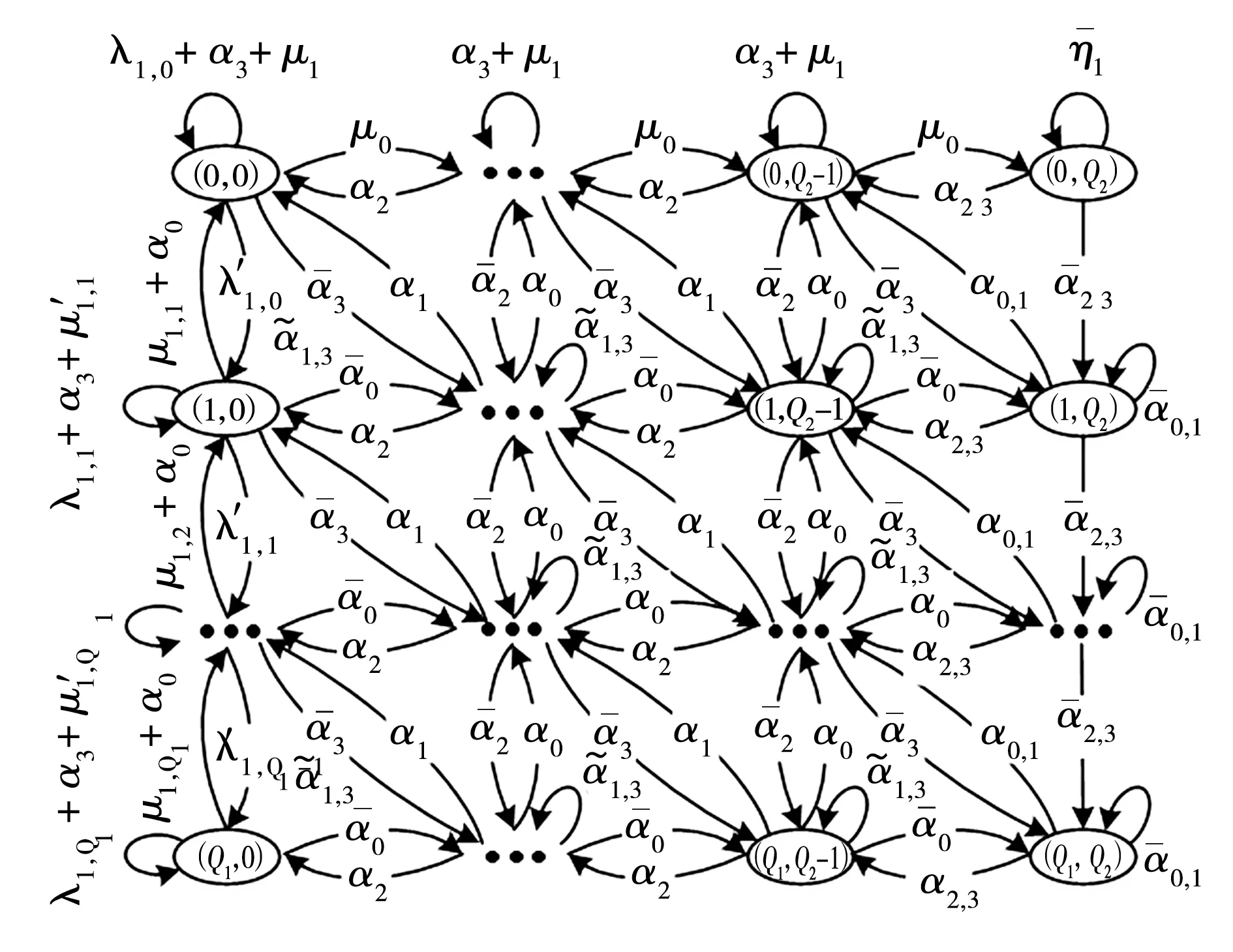
图2 Markov链模型Fig. 2 Markov chain model

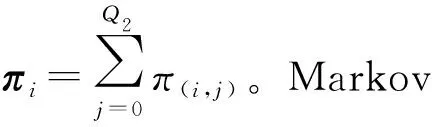
定理1Markov链的局部平衡方程为

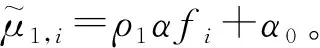
令Q1Q2×Q1Q2的矩阵M表示转移概率矩阵，稳态概率π(i,j)应满足约束条件Mπ=π，其中向量π定义为

π=[π0,0,π0,1,…,π0,Q2,π1,0,π1,1,…,

π1,Q2,…,πQ1,0,πQ1,1,…,πQ1,Q2]T，

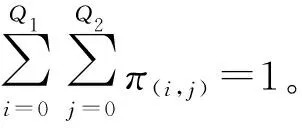
2 能量与时延

RSU数据队列的排队时延与消耗备用电池能量产生的平均传输功耗之间存在折中优化关系。

2.1 平均排队时延

2.2 平均功率

定理2从备用电池获取的平均功率为

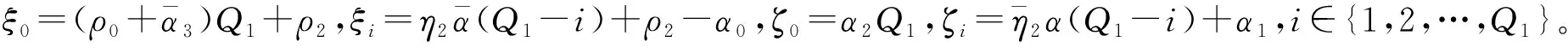
证明由于仅当无收割能量可用时，才会有可能使用备用电池能量，因此，平均功率为

(4)

由式(3)可得

(5)

因此，式(4)可写成

根据图3的Markov链，局部平衡方程可重写为

(6)

(7)

将式(7)代入式(4)中，平均功率表示为

证毕。

2.3 优化问题的建立

接着考虑定理1的平衡方程，从而得到约束条件

(8)

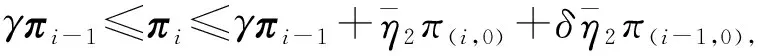
3 调度策略与最优解

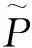
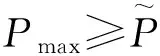
(9)

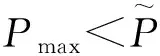
(10)

当RSU数据队列长度小于阈值时，此时队列中数据量少选择等待能量收割保持静默不传输的策略；而当队列长度等子阈值时，采取以最优概率选择性传输的策略，完成调度传输；而当队列长度已超过阈值，排队数据较多，此时只要有可使用的能量就传输数据。

4 仿真实验

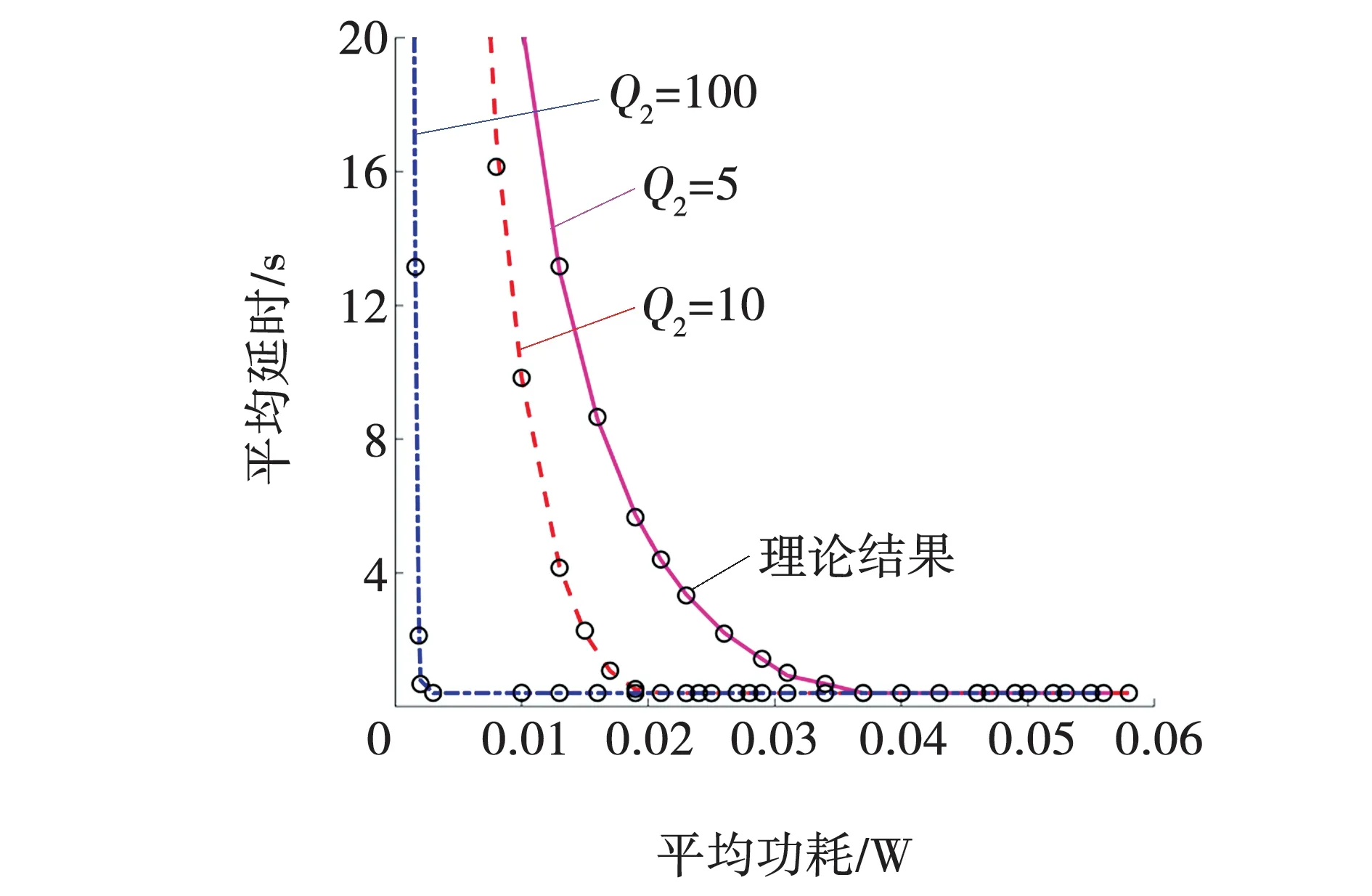
图3 不同能量队列长度下的时延-功率折中曲线 Fig. 3 Optimal delay-power curves for different energy queue length

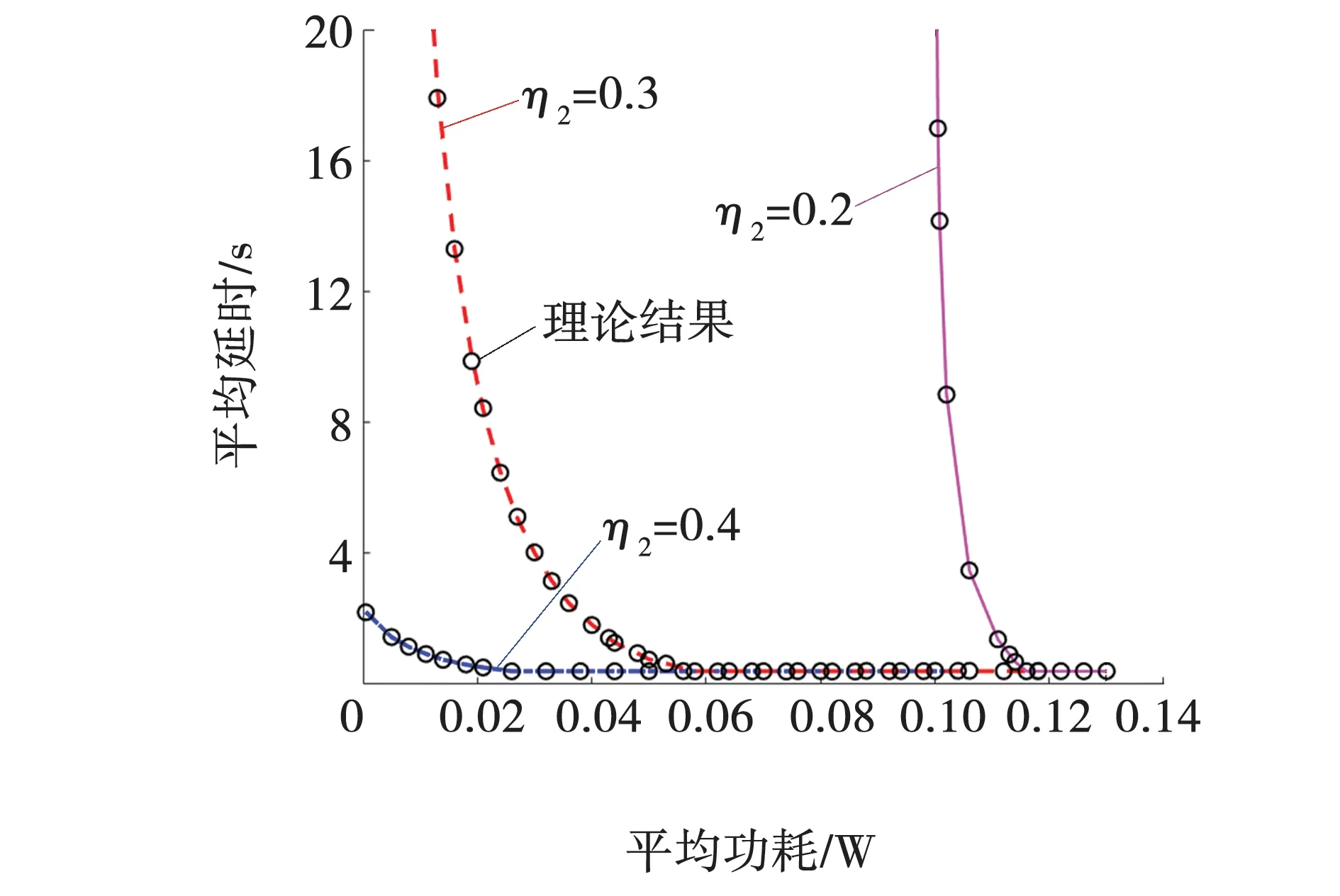
图4 不同能量包到达率下的时延-功率折中曲线Fig. 4 Optimal delay-power curves for different energy harvesting rate

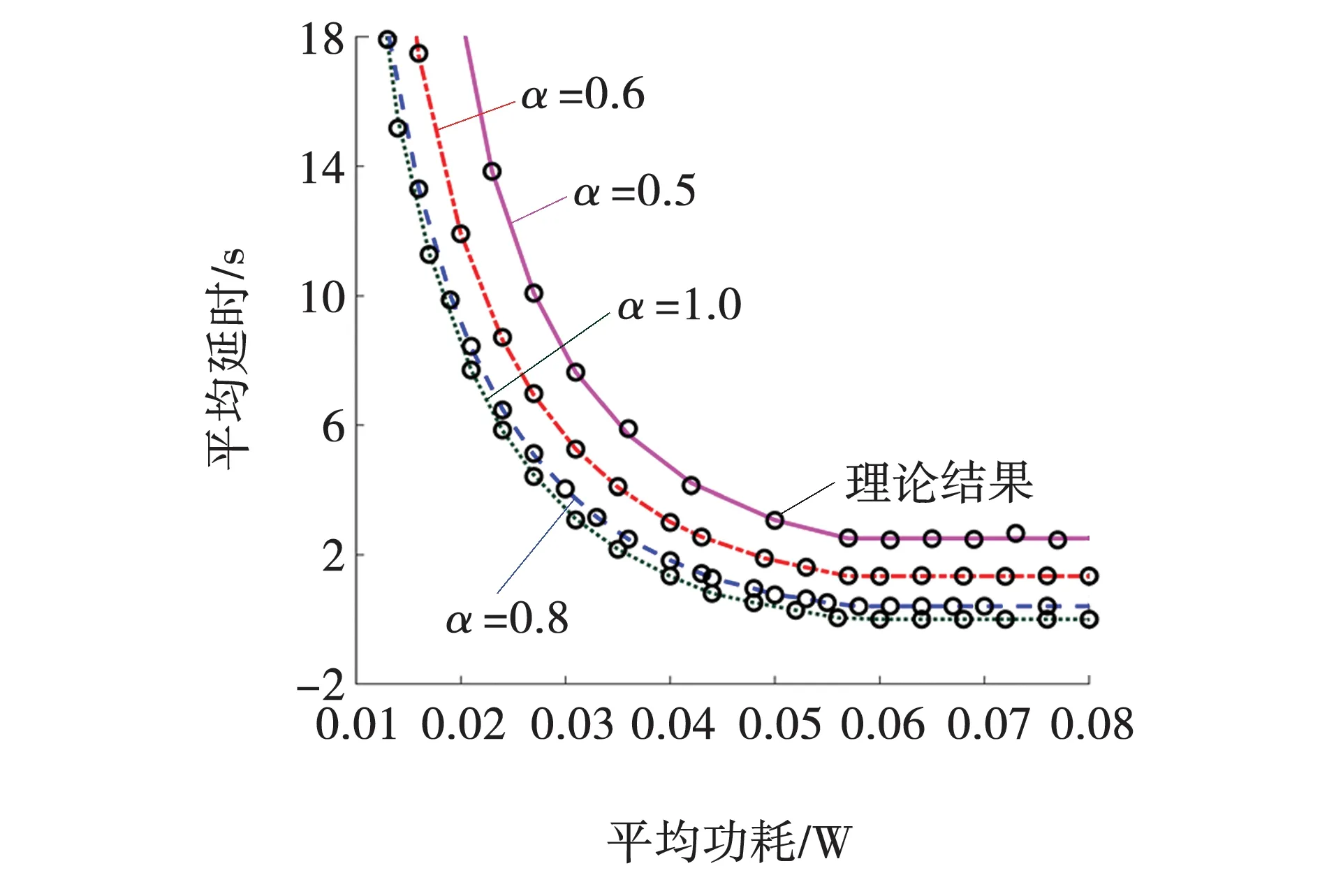
图5 不同“车-路”通信链路建立成功概率下的时延-功率折中曲线Fig. 5 Optimal delay-power curve for different probability of ‘vehicle-road’communication link establishment

从图3可以看出，理论计算结果和仿真结果一致吻合，验证式(8)线性规划问题求解的正确性。同时也可以看出，图中曲线单调递减且呈现门限线性的特点，当Q2取值越小越明显，且随着平均功率约束逐渐减小，队列平均时延增长却十分迅速。此外，随着收割能量电池容量Q2的增大，曲线下降的十分陡峭，即意味着为了达到同样的平均排队时延，电池容量较小时需要付出更多的功率，因为收割能量电池容量越小，为了获得同样的排队时延，需要消耗更多的备用电池功率，减小使用寿命。从图4可以看出，收割能量包到达率与数据包到达率的大小对比关系对整个曲线变化有很大的影响。当η1<η2时，即收割能量包的到达速率要快于数据包的到达速率，意味着有足够的收割能量用来传输，很容易就能获得很小的平均排队时延；相反，当η1>η2时，即收割能量包的到达速率慢于数据的到达速率，为了获得同样的排队时延，需要消耗更多的备用电池功率，且曲线变化十分陡峭。

从图5可以看出，对于每一条曲线，平均排队时延都随着平均功率约束的增加而减小，且下降趋势比较明显。其原因是当平均功率约束受限力度大，可用能量少时，基于调度策略会导致更多数据包将在队列中等待时间更长，随着功率约束逐渐放松，可用能量增多，平均排队时延就会有比较明显的变化。当可用平均功率足够大时，即在需要时总是有能量用来传输，此时平均排队时延仅取决于数据包的到达率和通信链路是否空闲的情况，曲线接近于平缓保持不变。另一方面，当通信链路建立成功概率越小，意味着过往车辆少，对于RSU来说，用来传输数据的机会少，那么更多的时隙都处于等待状态，导致平均排队时延增大。

5 结 论

(1)提出车路协同下“车-路”通信中，混合供电模式下，具有随机能量获取和功耗约束的平均时延最小优化调度策略。RSU采用概率调度策略，利用Markov链，得到了平均排队时延和功耗约束的数学表达式，进一步将时延-功耗优化问题转化为以数据队列的稳态概率为优化变量的线性规划问题。

(2)仿真结果表明，最优调度策略具有门限结构，这说明只有当数据缓冲区中的队列长度大于阈值时，才应该使用非再生能源进行传输，且各折中曲线呈分段线性，且每一个分段内都有对应传输策略。