一种减小同步正交网网间干扰概率的跳频表生成算法设计与验证

李红卫，林创勤，廖剑镖

(1.广东交通职业技术学院，广东 广州 510800；2.广东省船舶自动化工程技术研究中心，广东 广州 510800)

0 引 言

跳频通信技术在现代通信中具有广泛的应用。跳频组网是跳频通信装备发挥效能的重要途径，目前国内外对跳频组网的研究主要集中于同步组网和异步组网技术等方面。所谓同步或者异步均是指跳频网与网之间在射频时序上的制约关系，不能将单独的跳频网归结为同步组网或异步组网。

跳频组网主要包括频分组网和码分组网两大类：频分组网与常规通信频分组网类似，不同的跳频网络使用不同的跳频频率；码分组网：所有跳频网络在相同的跳频频率表上跳频，不同的跳频网络使用不同的跳频图案。根据跳频图案正交与否又分为正交跳频网和非正交跳频网。根据是否具有统一的时间基准，跳频组网可分为同步组网和异步组网。同步组网时，各跳频网络具有统一的时间基准。异步组网时，各跳频网络没有统一的时间基准。正交跳频网为了使跳频图案不发生重叠，要求全网做到严格定时，故一般采用同步组网方式。因此，从严格意义上讲，正交跳频网是同步正交跳频网，一般简称为同步网。非正交跳频网的跳频图案可能会发生重叠，因此可能会产生网间干扰。通过精心选择跳频图案和采用异步组网方法，可以使网间干扰减小到最低限度。

1 跳频组网参数

跳频电台工作的主要参数有：频率集(FQR)、实时时钟(TOD)、网络时钟(TON)、密钥(KEY)、跳频表、伪随机序列发生器(PRG)。FQR：是由

N

个频率组成的一个跳频频率集，记为{

f

,

f

,…,

f

}。TOD：代表跳频同步所必需的伪码发生器实时状态。TON：Time of Net，跳频系统的时间计数器，其单位为hop，其一般以网络中某台设备(如主台)的TOD为参照系。KEY：跳频系统的信道密钥，决定伪码发生器的初始状态。跳频表：是

K

行

N

列的矩阵，

K

是组网的个数。同步正交组网的跳频表满足条件：(1)的每行是{

f

,

f

,…,

f

}的一个排列；(2)的每列互不相同。

2 网间干扰分析

跳频伪随机序列发生器PRG的计算与TON和KEY有关，假定KEY为函数

g

，

g

为正整数集到{1,2,…,

N

}的映射。

同步正交跳频网要实现正常工作，须保证跳频网的每一起跳时刻相同，并且任一频率驻留时刻的各跳频网瞬时射频频率正交，理论上同步网在维持同步时，无网间干扰现象。同步组网的技术难度也在于必须保证各个跳频网间时钟严格同步，技术难度大。但实际中由于跳频技术体制装备不可避免会发生时钟漂移，且同步网各网之间的时钟信息交换会增加同步信息内容，同步时间增加，这些情况会导致网间干扰产生。

同步正交跳频网的网间干扰主要有2种情况：延时干扰和TON不一致的干扰。

延时干扰示意图如图1所示，其中

f

()和

f

()分别表示网

i

和网

j

的跳频表。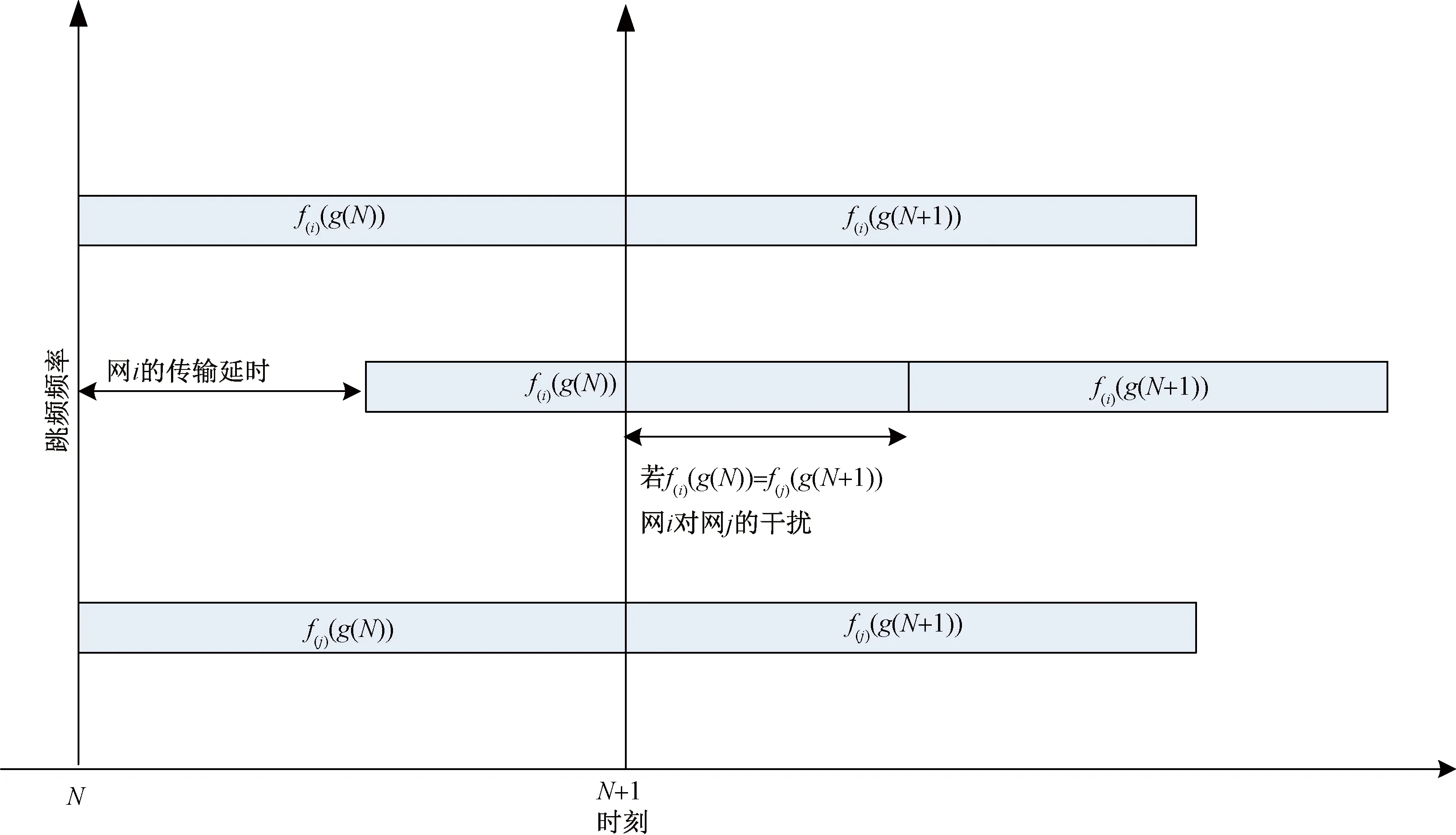

图1 延时干扰示意图

TON不一致干扰的示意图如图2所示。

图2 TON不一致干扰示意图

若

f

()(

g

(

N

))=

f

()(

g

(

N

+

l

))，则在时刻

N

，网

i

对网

j

会产生干扰。

对于延时干扰，延时不是整数跳时性能一般优于整数跳延时的性能，为了理论推导方便，只考虑延时为整数跳的情形，于是延时干扰亦可看作是TON不一致干扰。所以下文只考虑TON不一致干扰。

3 跳频表生成算法设计

3.1 跳频表交集矩阵与交集偏移量

本文定义给出跳频表的交集矩阵的概念，它是分析网间干扰和指导跳频表设计的一个重要量。

3.2 跳频表交集偏移量最小准则

(1) 网内存在2种TON值理论分析

网内的TON只有2个值，假设TON值为

K

和

K

，其中TON值为

K

的网有

k

个，TON值为

K

的网有

k

个，显然

k

+

k

=

k

。不失一般性，只考虑TON值为

K

的网受到TON值为

K

的网的干扰。称TON值为

K

的网为

K

-TON网。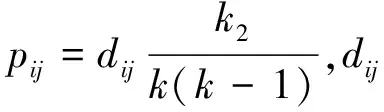

对于任何的跳频表，上述结论都成立。

(2) 网内存在3种TON值理论分析

网内的TON只有3个值，假设TON值为

K

、

K

、

K

，其中TON值为

K

的网有

k

个，TON值为

K

的网有

k

个，TON值为

K

的网有

k

个，显然

k

+

k

+

k

=

k

。不失一般性，只考虑TON值为

K

的网受到TON值为

K

的网和TON值为

K

的网的干扰。仍称TON值为

K

的网为

K

-TON网。任何时刻，某个

K

-TON网可能受到

K

-TON网和

K

-TON网的干扰，从而存在一定的干扰概率。令

p

(

s

,

t

)表示

g

(

K

)=

i

,

g

(

K

)=

s

,

g

(

K

)=

t

情形下，一个

K

-TON网受到的

K

-TON网或

K

-TON网干扰的概率。下面来分析

p

(

j

,

k

)。

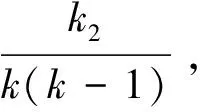
p

(

s

,

t

)=1-(1-

p

)(1-

p

)=

(1)

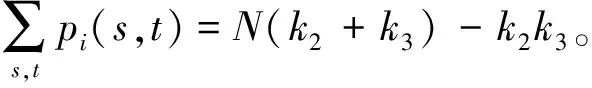
对于任何跳频表，上述结论都成立。

3.3 算法设计

由第3.2节可以看出，网内有2种或3种TON值时，均希望

σ

最小。所以设计跳频表的准则是使得交集偏移量

σ

最小。依据上述准则，可以利用如下算法通过计算机搜索较好的跳频表。跳频表的生成算法：

(2) 把的列进行随机置换，得方阵，再对的行进行随机置换，得方阵，并令为的前

k

行。(3) 计算

σ

，若

σ

<

σ

，则更新

σ

=

σ

，并更新=。返回(2)，直到循环次数到达上限。(4) 输出。

4 跳频表网间干扰概率验证

以

N

=16，

k

=10为例，进行10 000次搜寻的

σ

(按照与均值差的绝对值和计算)值的仿真图如图3所示。

图3 10 000次搜寻F的σF值仿真图

从仿真结果可知，只需要在最小

σ

对应的跳频表中找一个作为跳频表即可。以

N

=16，

k

=10为例，本例不经过优选，对采用如下常用跳频表的干扰概率进行分析。

其交集矩阵为：

由此可见，交集矩阵的分布很不均匀，可想而知性能不好。交集偏移量

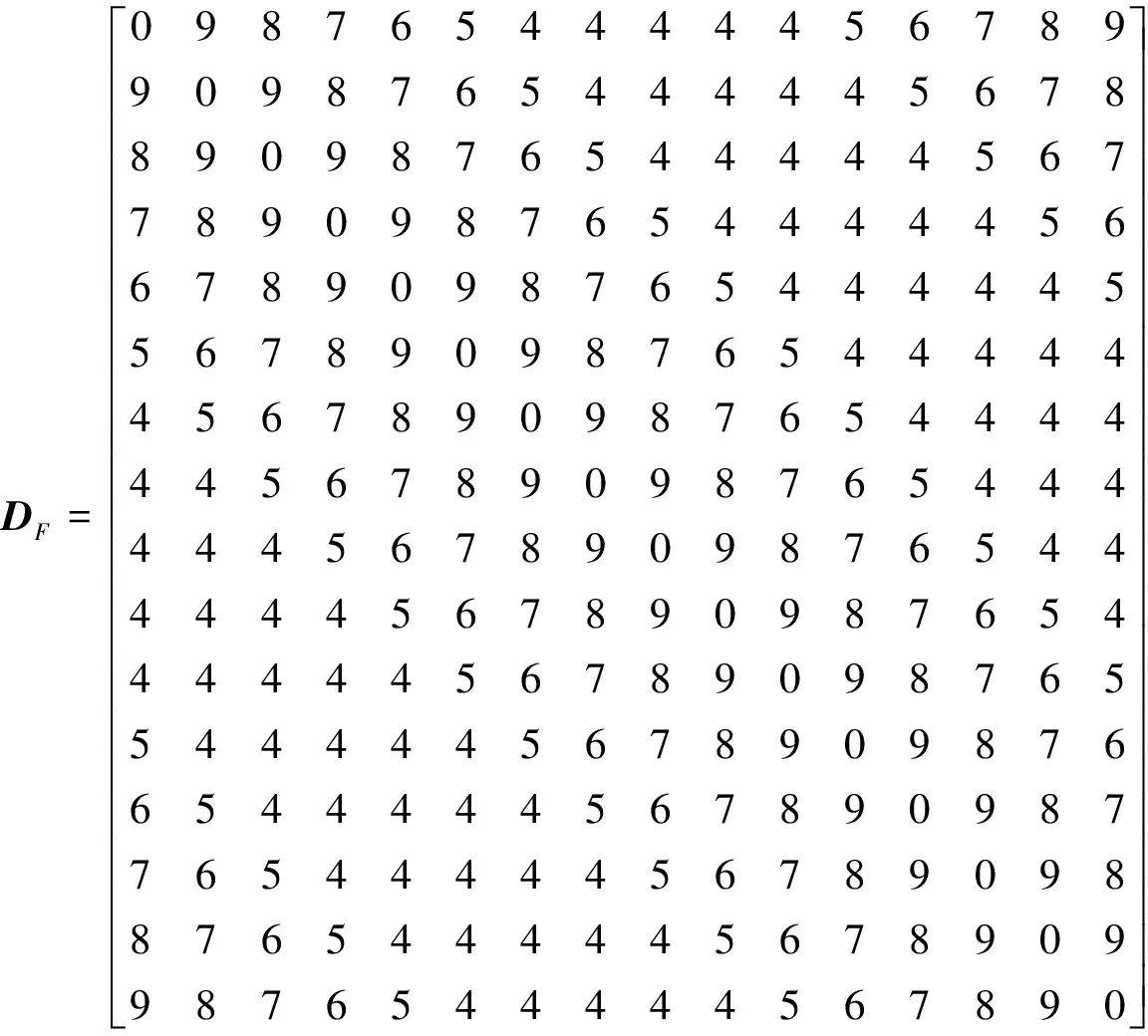
σ

为384，要远大于经过优选后

σ

的值。

以下是上述情况下几种不同情形的干扰概率的计算：

(1) 情形1:网络中有2个TON值，且

k

=1,

k

=9。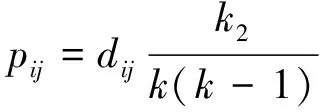

可以看出，

N

=16,

k

=10,

k

=1,

k

=9时，

K

-TON网的干扰概率为从0～0.9不等，而且如果密钥函数使得

g

(

K

)=

i

,

g

(

K

)=

i

+1或

g

(

K

)=

i

,

g

(

K

)=

i

-1时，

K

-TON网被干扰的概率高达0.9，这是不希望的。(2) 情形2：网络中有2个TON值，且

k

=2,

k

=8。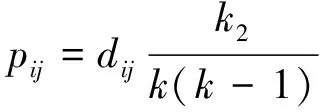

可以看出，

N

=16,

k

=10,

k

=2,

k

=8时，

K

-TON网的干扰概率为从0～0.8不等，而且如果密钥函数使得

g

(

K

)=

i

,

g

(

K

)=

i

+1或

g

(

K

)=

i

,

g

(

K

)=

i

-1时，

K

-TON网被干扰的概率高达0.8，这是不希望的。(3) 情形3：网络中有3个TON值，且

k

=1,

k

=1,

k

=7。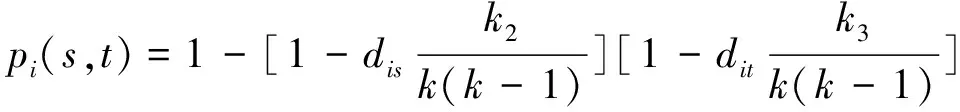

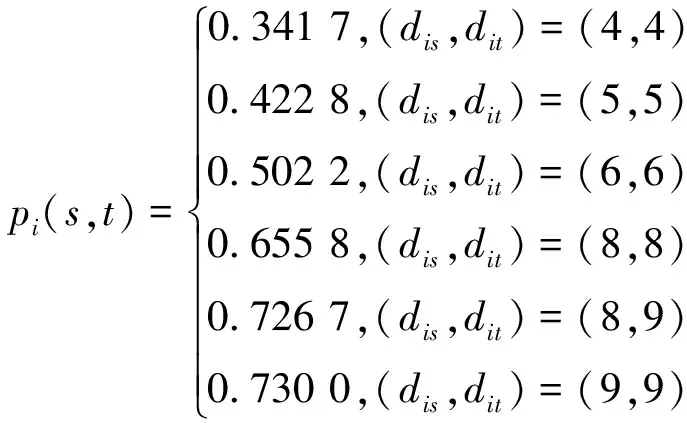
可见

p

(

s

,

t

)随着密钥函数

g

的变化，被干扰的概率变化是剧烈的，恶劣的情形下，密钥函数

g

可能导致

K

-TON网被干扰的概率为0.73。(4) 情形4：网络中有3个TON值，且

k

=1,

k

=2,

k

=6。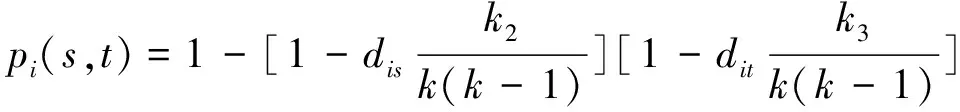

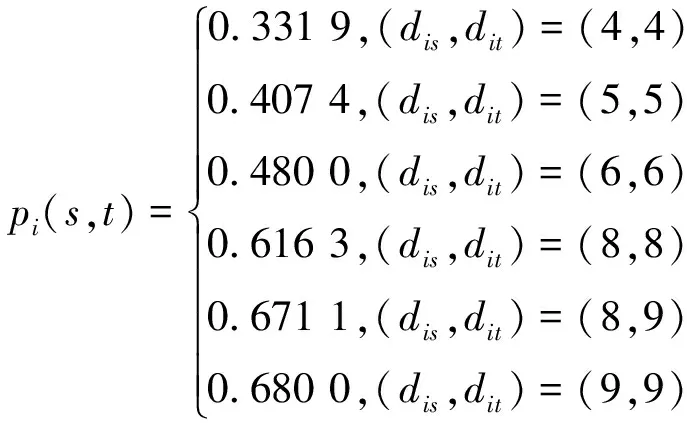
可见

p

(

s

,

t

)随着密钥函数

g

的变化，被干扰的概率变化是剧烈的，恶劣的情形下，密钥函数

g

可能导致

K

-TON网被干扰的概率为0.68。

5 结束语

本文分析了同步正交跳频网的网间干扰类型，针对TON不一致干扰从实际使用中存在2种和3种TON值进行理论分析，验证了所设计的跳频表交集偏移量最小准则的有效性，依据该准则设计了跳频表的生成算法，从跳频表网间干扰概率验证结果可以看出，以交集偏移量

σ

最小准则为指导，经过优选设计的跳频表的性能优于常用的跳频表的性能，而且基本上已经达到了最优(达到最优的条件是交集矩阵的分布是完全均匀的，均值跳频表的设计无关的定值)，充分说明本算法的有效性。