线性调频脉冲压缩信号旁瓣抑制分析
金德亚,张 玮
(解放军93448部队,天津 300270)
0 引 言
最初,脉冲雷达一般使用矩形脉冲信号。这种信号的优点是简单,缺点是无法兼顾探测能力和最大作用范围。宽脉冲信号同时包含了频率和相位两部分信息,对二者进行调制,便可增加信号中的宽带B
,从而克服探测能力和作用范围不能兼顾的缺点。采取调制的目的是将这样的信号用专门的接收器调制处理之后,可以有效地将脉冲压缩到一个适宜的宽度,也就是1/B
,如此便能增强信号的能力。这样的处理不仅可以增加雷达探测的最大距离,还可以提升其精度。这种信号被称为脉冲压缩信号,是一种线性调频信号,在当前各国使用的雷达中,它也是使用频率最高的一种信号。1 线性调频脉冲压缩信号
线性调频信号与普通信号不同,它的带宽更大,这是通过对非线性相位或线性频率的调制而实现的。
线性调频信号可表示为:
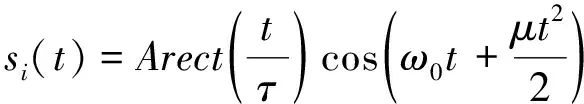
(1)
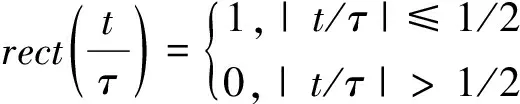
(2)
线性调频信号实质上是一种矩形脉冲信号,该信号具有特定的宽度τ
,但该宽度在载频的瞬间会随时间t
的变化而变化。计算其瞬时角频率的公式为: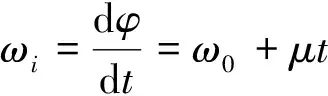
(3)
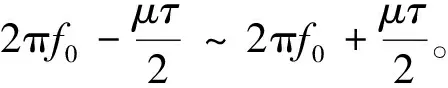

(4)
线性调频信号进入雷达接收系统时需要特殊的接收器进行压缩,该接收器将信号接收、压缩处理后,会进行匹配滤波,其经过滤波匹配后的信号输出增益与时间关系,利用MATLAB进行仿真,仿真结果如图1所示。

图1 线性调频压缩信号滤波匹配后输出波形
雷达接收机在使用线性调频压缩信号后,不仅在距离方面有所增加,在高度上也得到很大提升。该信号具备一些其他脉压信号不具备的长处,比如:对于多普勒频移的敏感度很低,很多回波信号都可以用同一个滤波器进行处理,这就使得信号的处理系统不需要像之前那样复杂;线性调频信号的生成和处理难度都得到很大降低,且技术上比较成熟;加之,由于其发射功率的峰值不高,该信号的隐蔽性极高,不会轻易被对手截获。但线性调频压缩信号也不是完美无缺的,其不完美之处在于距离和多普勒频移的耦合与相应滤波器的输出旁瓣不够低。
2 旁瓣抑制处理分析仿真
滤波器所接收和处理的信号是线性调频信号,在被接收系统压缩之后,形成具有辛克函数特征的窄脉冲,然后输出。输出脉冲包含2个部分:主瓣及多个旁瓣,旁瓣是在时间轴之上延伸而出的。众多旁瓣的峰值具有一定的规律:离主瓣越近,峰值越高,比如最近的峰较主峰的差距为13.46 dB,距离次之的峰较前者差4 dB,余者依此类推,各瓣间隔1/B
。雷达工作时会接收回波信息,其中反射面积存在巨大差异的地方就是需要重点关注之处。旁瓣会对返回信号造成干扰,所以,雷达运行时,这种干扰绝对不能出现。只有成功排除旁瓣的干扰,才能将该信号成功运用在雷达上。失配处理(旁瓣抑制或加权技术)可以对付这种情况。加权可以分为许多种,比如:时域加权,为得到多普勒响应而对波的形状加以控制;频域加权,为得到压缩脉冲形状,对频谱的幅度加以调整。但不论是哪一种方法,其根本目的都是将其涉及到的旁瓣消除。2.1 加权窗函数
将加权这一技术应用到本领域,虽然可以很好地降低旁瓣影响,但也会对输出信号造成影响,比如主瓣变宽、降低等。信噪比本身就存在一定的损失,而采用此技术会将损失加大,-3 dB主瓣加宽系数也会增大。各种窗函数性能比较如表1所示。
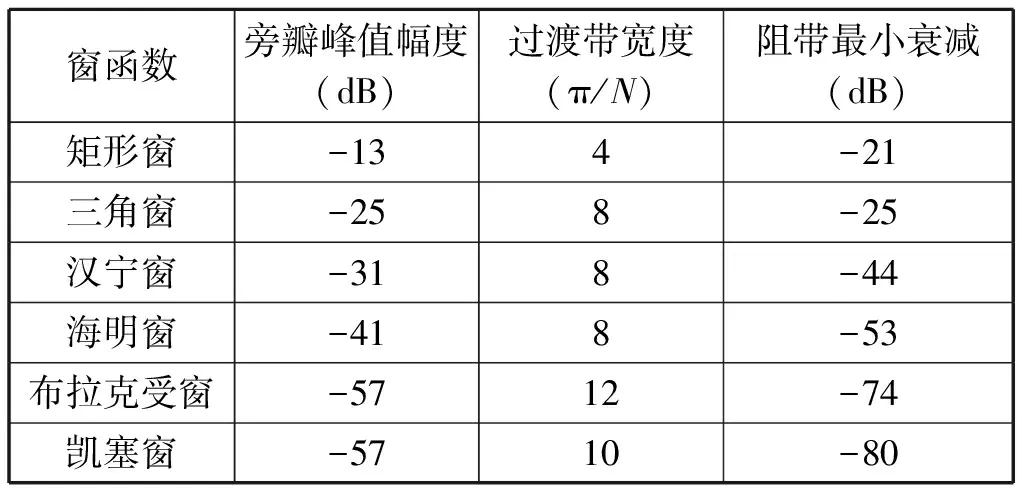
表1 各种窗函数性能比较
海明窗函数可以对升余弦加以改进,用公式可以表示为:

(5)
汉宁窗函数可以用来计算余弦平方,用公式可以表示为:
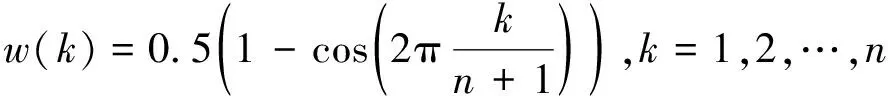
(6)
2.2 加窗处理的分析仿真
对单路信号进行处理时,不管是脉冲压缩还是加窗,在处理时是不分先后的。处理之后,将二者合并便得到了雷达所需波形。信号在实际应用中,都要对压缩后的波形进行处理,也就是加窗。这种处理有很多种,比如加布拉克曼窗、矩形窗、凯塞窗等。不同旁瓣与主瓣的距离不同,窗函数也会出现相应的变化,甚至加权后在-3 dB处主瓣加宽的程度出现巨大的差异。图2为分别使用了汉宁窗和海明窗处理后,利用MATLAB进行仿真的波形图。
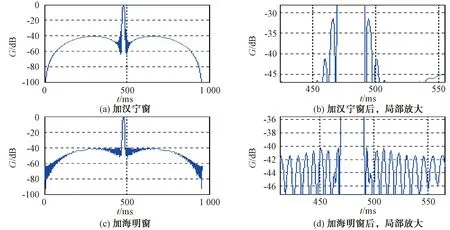
图2 信号经过汉宁窗和海明窗处理后的波形图
从局部放大图中可以看出,加汉宁窗后,最高距离旁瓣可以抑制到30 dB以下,大约为31 dB。加海明窗后,最高距离旁瓣可以抑制到40 dB以下,大约为41 dB。
加窗处理可以采用2个或3个窗函数串联,它们可以是同一个窗函数,也可以是不同的窗函数。旁瓣电平得到进一步降低,随之而来的是,-3 dB主瓣的加宽系数和信噪比的损失都有明显的上升。将2个海明窗串联在一起,可以看出旁瓣能降低到-50 dB以下,要比单独用1个海明窗时效果好,另外2个数值的变动也极为突出,比如:信噪比(dB)的损失一开始只有1.34,在串联之后增加了1.16;而-3 dB主瓣加宽系数原来只有1.47,在串联之后,数值明显上扬了0.566。若用海明窗和汉宁窗串联,也可得到同样的结论。比较其它窗函数相互串联抑制距离旁瓣的效果,可见旁瓣电平降低的同时,-3 dB主瓣的加宽系数和信噪比损失都有明显的上升。图3为信号经过加2个海明窗串联和加海明窗与汉宁窗串联处理后的波形图。
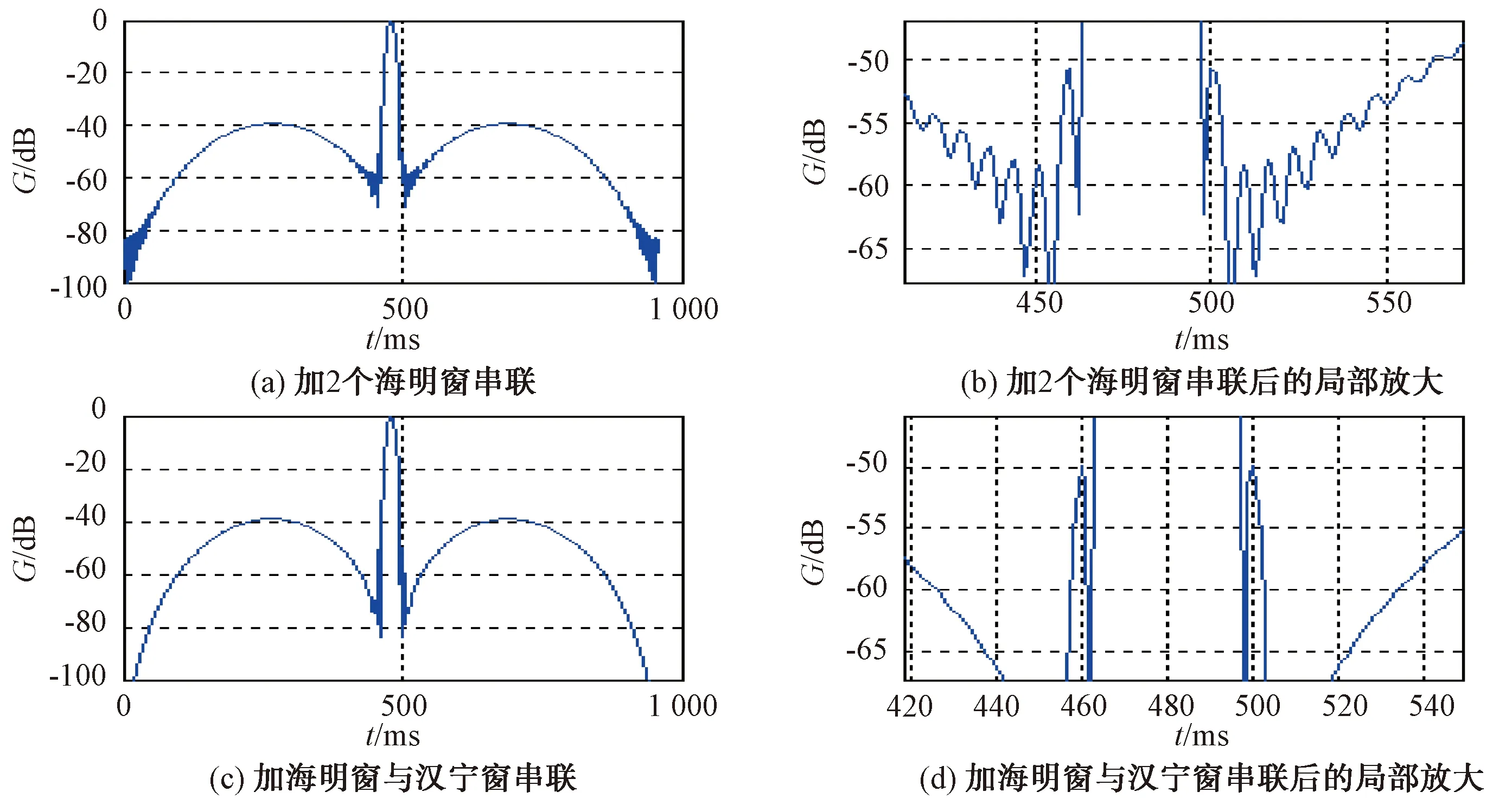
图3 信号经过加2个海明窗串联和加海明窗与汉宁窗串联处理后的波形图
3 结束语
为了改善脉冲压缩雷达的检测性能,提高分辨多目标的能力,对线性调频信号脉冲压缩输出波形中的干扰因素(比如旁瓣),采取加窗的方式加以抑制。通过模拟分析可以发现,去除旁瓣干扰是以主瓣变宽和信噪比损失变多为代价的。这就导致雷达距离分辨率大大下降。为了提高距离分辨率和降低旁瓣,只能在旁瓣抑制、主瓣加宽、信噪比损失、旁瓣衰减速度以及技术实现难易等方面折衷考虑,选择合适的加权函数,从而提升其技术方面的需求。

