磁流变阻尼器神经网络模型的建立及优化

王伟江，闫 兵，徐昉晖，董大伟

（1.先进驱动节能技术教育部工程研究中心，四川 成都 610031；2.西南交通大学机械工程学院，四川 成都 610031）

1 引言

磁流变阻尼器是一种以磁流变液为载体的智能振动控制装置，在外加磁场的作用下可以实现毫秒级的液体流变特性转变，从而使其阻尼力在较宽范围内连续可控，为发动机的有效宽频隔振提供了重要手段[1]。以磁流变阻尼器作为执行器的前提是建立准确的阻尼器动力学模型，但由于磁流变液在磁场作用下为非牛顿流体，导致阻尼器存在复杂的非线性磁滞特性。目前对其动力学模型的研究主要分为参数化模型和非参数化模型两类。

文献[2]建立了Bingham模型，该模型简单，参数少，但无法描述阻尼器在屈服前，其阻尼力与速度的关系；为此文献[3]提出了修正Bounc-Wen模型，该模型能较好地反应磁流变阻尼器的非线性特性，但其模型参数多达14个，辨识困难；文献[4]对试验数据进行拟合，得到了磁流变阻尼器多项式模型；文献[5]采用分数微积分理论，建立了分数阶Zener模型，并探讨了阻尼器在该模型下的粘弹性。参数化模型通常用来描述磁流变阻尼器的正向模型，很难通过公式推导得到其逆向模型，而逆向模型又是实现发动机隔振半主动控制中关键的一环，因此采用神经网络的非参数化模型越来越受到重视。文献[6]在磁流变阻尼器非参数化建模中采用自适应神经模糊系统理论，避免了参数化建模存在的大量参数辨识问题；文献[7]以贝叶斯推理分析框架下的非线性自回归神经网络技术建立了磁流变阻尼器的正向模型，该模型可以有效地预测磁流变阻尼器在周期和随机激励下的非线性动态行为；文献[8]通过对磁流变阻尼器双曲正切滞回模型和BP神经网络模型的辨识精度比较，指出了神经网络建模的优势；文献[9]指出BP神经网络初始权值和阈值对网络训练速度和精度的影响，并在磁流变阻尼器正、逆向建模中采用遗传算法对BP神经网络进行优化，提高了神经网络的训练效率和精度，但并未考虑遗传算法存在的早熟和收敛速度慢等问题。可以看出，基于神经网络的非参数化模型在磁流变阻尼器建模得到了广泛的应用，这一点在逆向模型中尤为明显，但针对神经网络存在收敛速度慢和局部极小化问题的研究并不充分。

以磁流变阻尼器动力学性能试验结果为基础，通过统计学方法确定了该阻尼器正向、逆向模型的BP神经网络结构；并提出一种结合适应度线性变换、自适应交叉和变异概率的改进遗传神经网络（IGA-BP）算法，建立了磁流变阻尼器非参数神经网络模型，有效地克服了传统遗传神经网络（GA-BP）早熟和收敛速度慢的问题，提高了模型的训练效率和辨识精度，为发动机隔振半主动控制奠定基础。

2 改进GA-BP神经网络模型

在非线性系统建模中，为减小BP神经网络初始权值和阈值随机选取的影响，常用遗传算法进行优化，但受传统遗传算法影响，GA-BP神经网络存在早熟和收敛速度慢的问题，为此文中从选择、交叉、变异方面进行改进，以提高模型的训练效率和辨识精度。

2.1 BP神经网络

前馈型BP神经网络可以实现复杂非线性系统的建模，具有单隐含层的网络拓扑结构，如图1所示。X1，X2，···Xn为神经网络的输入；Y1，Y2，···Ym为神经网络的输出；ɑj、bk分别为BP神经网络隐含层和输出层神经元的阈值；ωij、ωjk分别为输入层和隐含层及隐含层和输出层间的连接权值。

图1 BP神经网络结构图Fig.1 Structure of BP Neural Network

BP学习算法通过误差反向传播不断调整网络的权值和阈值，具有自学习能力，包含了正向、反向传播两个阶段。在正向传播中，输入信号从输入层输入，经隐含层传递至输出层，每一层的神经元只能影响下一层神经元状态；在反向传播中，误差信号沿原来通道返回，通过不断修正权值和阈值使得误差均方值最小。但因网络的初始权值和阈值均为随机值，在磁流变阻尼器模型辨识中易出现收敛速度慢，局部最优问题，可采用遗传算法进行优化。

2.2 遗传算法及改进

遗传算法是模拟生物遗传和进化过程而建立起来的一种全局寻优算法，具有较强的鲁棒性和全局搜索能力。其基本流程包含编码、适应度计算、选择、交叉、变异。文中采用实数编码方式，以预测值与实际值之间均方根误差为适应度，分别从选择、交叉、变异环节对遗传算法改进，克服其早熟和收敛速度慢的问题。

2.2.1 改进选择算子

遗传算法有多种选择算子，使用最广泛的是比例选择算子和最优保存策略，其中，最优保存策略是遗传算法收敛性的一个重要保证条件，但易破坏种群多样性，促使算法早熟，造成局部收敛[10]。

在最优保存策略的基础上，采用的线性比例变换法对个体适应度进行尺度变换，维持个体适应度值间的合理差异，可在算法早期抑制某些超级染色体，克服早熟，在算法晚期加速竞争，提高收敛速度，如式（1）所示。

式中：f，f′—变换前后个体适应度值；fmin，fɑvg，fmax—变换前种群中个体最小、平均和最大适应度值；c—常数，当种群规模为（50～100）时，c可取（1.2～2）。

若种群中某些个体适应度远低于当代种群平均值时，有可能出现变换后适应度为负的情况，为此考虑到变换后最小适应度非负的条件，可进行如下变换：

若不等式（4）满足，则执行式（2），否则执行式（3）。

2.2.2 交叉算子和变异算子改进

交叉概率pc和变异概率pm是影响遗传算法收敛性的关键，基本遗传算法中，pc和pm为固定值，针对不同优化问题，需反复试验来确定，且很难找到最佳值。Srinvivas等提出了自适应遗传算法，其pc和pm随个体的适应度进行线性调整，如式（5）、式（6）所示。

式中：f ″—进行交叉的两个个体中较大的适应度值；f—变异个体的适应度值；k1，k2，k3，k4—在(0，1)区间取值。

可以看出，在上述算法中个体适应度值越大，对应的交叉和变异概率越小，促使适应度值小于平均适应度的个体进行交叉和变异，提高种群的多样性；同时对于适应度值高于平均适应度的个体，减小其被破坏的概率，促进算法收敛；但当个体适应度值等于最大适应度值时，其交叉和变异概率为零。这种算法适应于进化后期的种群，在进化初期易使算法产生早熟。为此，文中采用文献[11]提出的改进算法，使种群中最大适应度个体的交叉和变异概率不为零，如下：

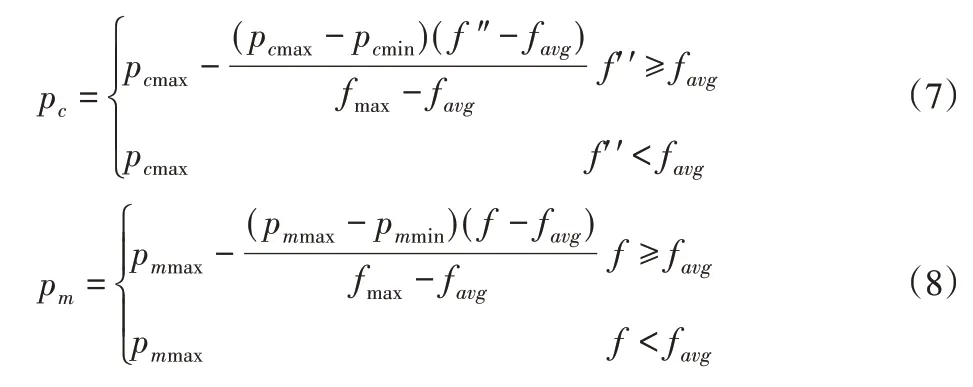
式中：pcmax，pcmin，pmmax，pmmin—交叉和变异概率的取值上限和下限。

2.3 改进GA-BP神经网络模型

改进GA-BP（IGA-BP）神经网络算法的基本流程，可分为BP神经网络结构确定、改进遗传算法寻优和BP神经网络预测三个部分，如图2所示。其中，BP神经网络结构确定部分根据磁流变阻尼器的动力学特性确定网络结构，进而确定遗传算法中个体长度；自适应遗传算法以BP神经网络辨识的均方根误差为适应度进行全局寻优，找到最优的权值和阈值；BP神经网络预测时，以遗传算法的寻优结果为初始权值和阈值，通过训练得到最终的神经网络非参数化模型。

图2 IGA-BP算法流程Fig.2 Flow of IGA-BP Algorithm

3 磁流变阻尼器动力学试验

使用电液伺服材料试验机对磁流变阻尼器进行动力学性能测试，如图3 所示。以试验机主动夹头驱动磁流变阻尼器的活塞，使其相对于缸体以固定的频率和振幅作简谐运动，同时由直流电源提供稳定的电流输入。试验简谐激振幅值为1mm，激振力频率为（1～47）Hz，间隔2Hz；输入电流为（0～2）A，间隔0.5A；同时记录磁流变阻尼器输入电流，位移，速度，频率及输出阻尼力。

图3 磁流变阻尼器动力学试验平台Fig.3 Magnetorheological Damper Dynamics Test Platform

不同电流时，在1Hz正弦激励下磁流变阻尼器位移—阻尼力和速度—阻尼力的滞回曲线，如图4所示。由图可见，在无输入电流（0A）的情况下，阻尼力较小，主要由磁流变液的粘性及活塞与密封圈间的摩擦产生；随着电流的增大，阻尼力逐渐增加并趋于饱和。当活塞速度较小时，阻尼力随速度的增大而快速增加，当速度增大到一定程度后，阻尼器表现出屈服现象，阻尼力增速减缓。可见磁流变阻尼器具有很强的非线性磁滞特征。

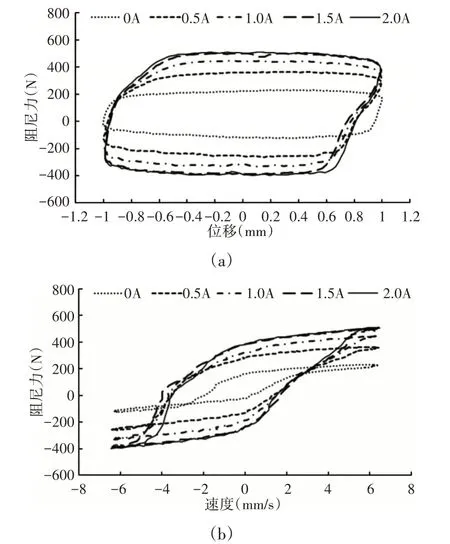
图4 不同电流下的滞回特性曲线（1mm，1Hz）Fig.4 Measured Hysteresis Loops Under Different Current Levels（1mm，1Hz）

4 磁流变阻尼器模型辨识

4.1 IGA-BP神经网络正向模型

正向模型是根据阻尼器的状态对其当前时刻输出阻尼力的预测模型。根据文献[9]可知，磁流变阻尼器性能与前一时刻的状态有关，故分别以阻尼器前一时刻的位移sk-1，速度vk-1，电流Ik-1，阻尼力fk-1和当前时刻的位移sk，速度vk，电流Ik为输入，当前时刻的阻尼力fk为输出。据此，可确定神经网络正向模型具有7个输入神经元，1个输出神经元，但隐含神经元个数尚待确定，且对于不同问题最优隐含神经元个数不一定相同。为避免神经网络结构对正向模型辨识精度的影响，文中分别对含有（5～25）个隐含神经元的BP神经网络进行200次测试，并进行误差统计，如图5所示。可见，随着隐含神经元个数增达，网络具有更强的学习能力，均方根误差整体呈减小趋势，但网络参数数目也随之增加，增大了模型训练的计算量，且将可能导致过拟合现象。综合考虑统计误差和计算量，隐含神经元个数选为18个。

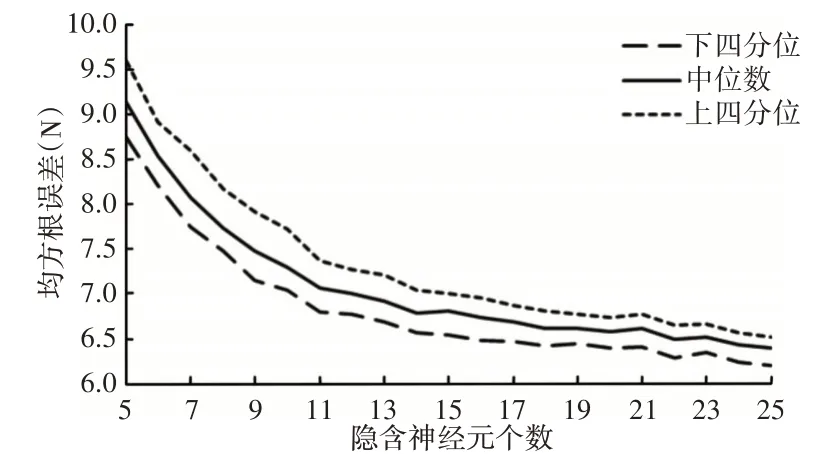
图5 不同隐含神经元数目下的模型均方根误差统计Fig.5 RMSE Analysis for Different Numbers of Hidden Neurons

基于上述研究，可确定磁流变阻尼器正向模型的神经网络结构为7-18-1，共有144个权值，19个阈值。由此可确定遗传算法中的个体长度，取遗传算法种群规模为80，最大迭代次数为100，pcmax，pcmin，pmmax，pmmin分别取0.8，0.5，0.1，0.001，选取每个输入电流下，磁流变阻尼器在11Hz、25Hz和39Hz的试验数据作为辨识精度的测试样本，其余试验数据作为训练样本，对BP、GABP和IGA-BP神经网络正向模型进行训练。

GA-BP算法和IGA-BP算法的最佳适应度和平均适应度曲线，可以看出：改进后的遗传算法收敛速度更快，在第50代即可收敛，且精度更高，其最佳适应度最小值为5.05，如图6所示。激振力频率11Hz时，在各输入电流下阻尼力的预测结果，由图可知阻尼力预测值与测试值误差很小，可见文中建立的正向模型能很好地描述磁流变阻尼器的正向动力学特性，如图7所示。不同电流时BP、GA-BP及IGA-BP神经网络正向模型的预测均方根误差，可知相对于BP神经网络，GA-BP和IGA-BP神经网络正向模型的辨识精度都有不同程度地提高，且后者的精度更高，如表1所示。

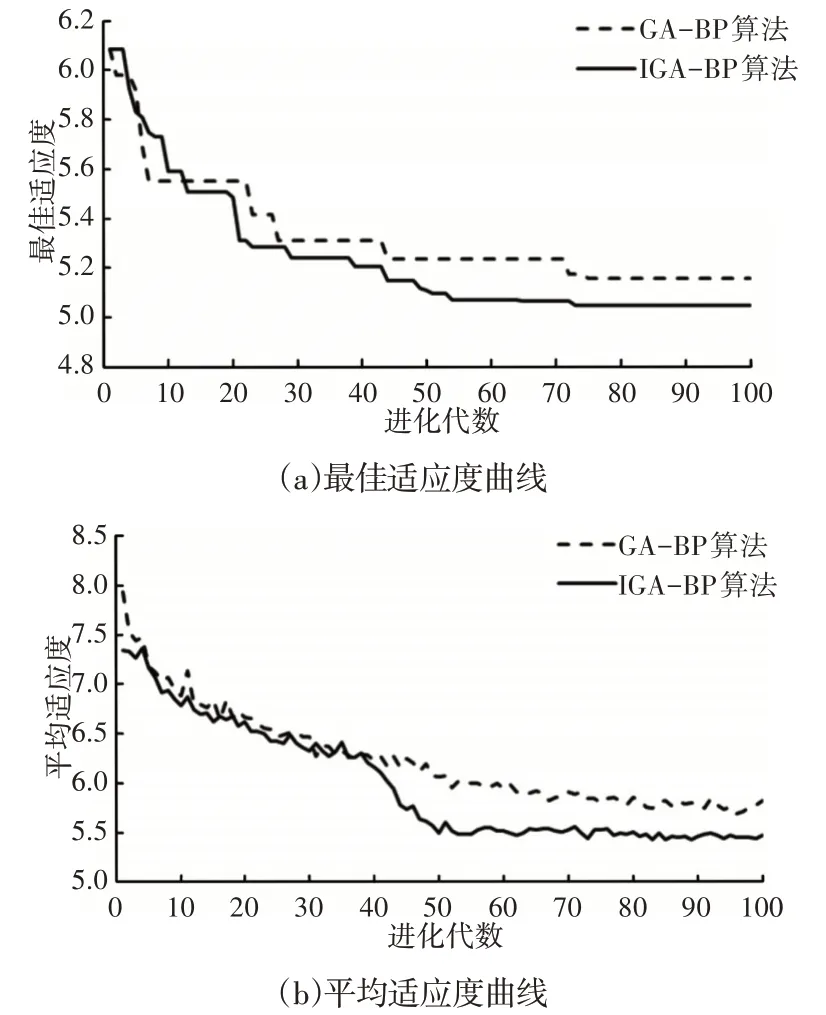
图6 适应度值进化曲线Fig.6 Evolution Curve of Fitness Value

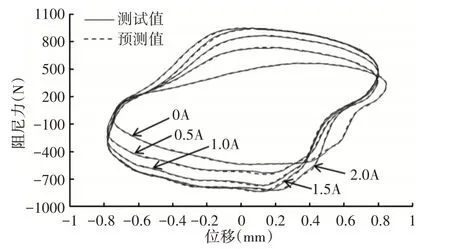
图7 IGA-BP神经网络预测输出阻尼力Fig.7 Output Damping Force Predicted by IGA-BP Neural Network

表1 神经网络不同电流时的预测均方根误差（N）Tab.1 Prediction RMSE of NN with Different Currents（N）

4.2 IGA-BP神经网络逆向模型

逆向模型是根据阻尼器的状态对其当前时刻输入电流的预测模型。以阻尼器前一时刻的位移sk-1，速度vk-1，电流Ik-1，阻尼力fk-1和当前时刻的位移sk，速度vk，阻尼力fk为输入，当前时刻的电流Ik为输出，建立包含7个输入神经元，1个输出神经元的神经网络逆向模型。为确定逆向模型的隐含神经元数目，同样分别对含有（5～25）个隐含神经元的BP神经网络进行200次测试，并进行误差统计，如图8所示。可见，对于该阻尼器而言，可能因网络过拟合的原因，逆向模型的统计预测误差随着隐含层神经元数目的增加呈增大趋势。这也说明尽管输入、输出神经元个数相同，但对于求解目标不同的神经网络正向、逆向模型，其最优隐含神经元数目并不一定相同。根据计算结果，选择逆向模型的隐含神经元数目为6个。

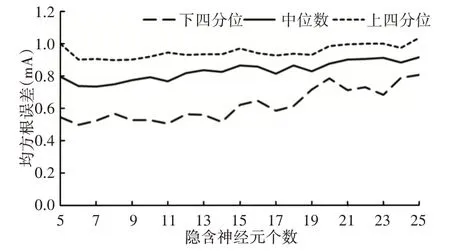
图8 不同隐含神经元数目下的模型均方根误差统计Fig.8 RMSE Analysis for Different Numbers of Hidden Neurons

因此，可确定磁流变阻尼器逆向模型的神经网络结构为7-6-1，共有48个权值，7个阈值，进而可得遗传算法中的个体长度。与正向模型训练过程相同，选择各输入电流下，11Hz、25Hz 和39Hz的试验数据作为辨识精度的测试样本，其余试验数据作为训练样本，对BP、GA-BP 和IGA-BP 神经网络逆向模型进行训练。GA-BP算法和IGA-BP算法最佳适应度和平均适应度曲线，如图9所示。可见：在逆向模型辨识中IGA-BP算法的收敛速度更快，在第18代左右即可收敛，且精度也有相应小幅提升。IGABP神经网络逆向模型的预测电流与测试电流对比，如图10所示。可见，该逆向模型的预测电流可以很好地跟随测试电流，因此该模型是有效的，能够表征磁流变阻尼器的逆向动力学性能。BP、GA-BP及IGA-BP神经网络逆向模型的预测均方根误差，可知三种逆向模型的均方根误差都较小，其中IGA-BP神经网络模型的整体误差最小，模型辨识精度最高，如表2所示。

表2 神经网络逆向模型预测均方根误差（mA）Tab.2 Prediction RMSE of Inverse Model（mA）

图9 适应度值进化曲线Fig.9 Evolution Curve of Fitness Value

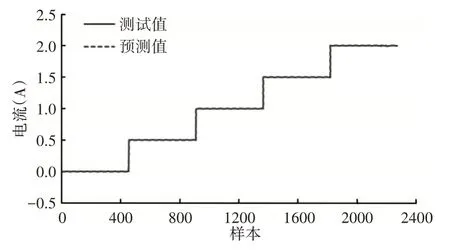
图10 IGA-BP神经网络预测电流Fig.10 Current Predicted by IGA-BP Neural Network

5 结论

以磁流变阻尼器动力学试验数据为基础，通过对神经网络非参数模型辨识建立了该阻尼器的正向、逆向模型。针对BP神经网络收敛速度慢和易局部极小化的问题，利用遗传算法对其初始权值和阈值优化，并对遗传算法进行改进，研究结果表明：

（1）随机选取初始权值和阈值会限制BP神经网络的训练速度和预测精度，利用遗传算法进行初始权值和阈值的优化可以取得良好的效果。

（2）基于IGA-BP神经网络的非参数化模型能更准确地反映磁流变阻尼器动力学特性，且对于求解目标不同的正向、逆向模型，其最优隐含神经元数目并不一定相同。

（3）提出的IGA-BP 神经网络算法可以有效克服GA-BP 神经网络早熟和收敛速度慢的问题，提高磁流变阻尼器正向、逆向模型的训练效率和辨识精度。