Development of Granular Fuzzy Relation Equations Based on a Subset of Data

Dan Wang, Xiubin Zhu, Witold Pedycz,, Zhenhua Yu, and Zhiwu Li,

Abstract—Developing and optimizing fuzzy relation equations are of great relevance in system modeling, which involves analysis of numerous fuzzy rules. As each rule varies with respect to its level of influence, it is advocated that the performance of a fuzzy relation equation is strongly related to a subset of fuzzy rules obtained by removing those without significant relevance. In this study, we establish a novel framework of developing granular fuzzy relation equations that concerns the determination of an optimal subset of fuzzy rules. The subset of rules is selected by maximizing their performance of the obtained solutions. The originality of this study is conducted in the following ways.Starting with developing granular fuzzy relation equations, an interval-valued fuzzy relation is determined based on the selected subset of fuzzy rules (the subset of rules is transformed to interval-valued fuzzy sets and subsequently the interval-valued fuzzy sets are utilized to form interval-valued fuzzy relations),which can be used to represent the fuzzy relation of the entire rule base with high performance and efficiency. Then, the particle swarm optimization (PSO) is implemented to solve a multiobjective optimization problem, in which not only an optimal subset of rules is selected but also a parameter ε for specifying a level of information granularity is determined. A series of experimental studies are performed to verify the feasibility of this framework and quantify its performance. A visible improvement of particle swarm optimization (about 78.56% of the encoding mechanism of particle swarm optimization, or 90.42% of particle swarm optimization with an exploration operator) is gained over the method conducted without using the particle swarm optimization algorithm.

I. INTRODUCTION

FUZZY sets and fuzzy rules are usually applied to form a rule-based system to build a data processing framework[1]–[5]. A typical fuzzy rule-based system contains three basic components: a collection of fuzzy rules (rule base), a database that collects membership grades used in the fuzzy rules, and a reasoning mechanism that provides relationships between the input and output variables. In typical fuzzy system modeling,fuzzy relation equations play an important role in representing the relationships between the input and output spaces [6], and they are strongly correlated to the final performance of the fuzzy rule-based system. Information granules [7]–[9], which are commonly constructed in the form of fuzzy sets [10]–[12]and positioned in the antecedent and consequent parts of the fuzzy rules in fuzzy rule-based systems [13], are critical to forming the fuzzy relation equations from both the conceptual and algorithmic perspectives.

A commonly encountered structure of fuzzy relation equation is represented as

whereAandBare the fuzzy sets defined in the finite input and output spaces, respectively. The solution to the fuzzy relation equation isR, which indicates the relationship between the elements positioned in the input and output spaces.

Usually, a system of fuzzy relational equations is considered as that the fuzzy sets formed in the input and output spaces(Ak,Bk),k= 1, 2 ,...,N, are associated in the following form:

Previous research mainly focuses on fuzzy rule-based systems [14] that are related to fuzzy relations, and they perform significant roles in reasoning of complex problems[15]–[17]. They provide various forms of fuzzy operations[18]–[21] from the conceptual aspects, which greatly promote the abilities of exploring different solutions to fuzzy relations.However, these fuzzy operations are built on a basis of numeric data. It is widely admitted that in fuzzy rule-based systems, a reasonable and feasible alternative is that both the antecedent and consequent parts of the fuzzy rules are characterized by information granules rather than numeric variables. Information granules [7]–[9] make significant contributions to improve the performance of fuzzy system modeling by providing a new way of representing and describing data at higher levels of abstraction. Different from traditional numeric models, one can directly improve the accuracy and interpretability of granular models by changing the level of information granularity flexibly. Thus, granular fuzzy relation equations are becoming increasingly noticed and widely researched in fuzzy system modeling.

When developing fuzzy relation equations, it becomes essential to improve their efficiency, especially for large-scale fuzzy systems [22] that are composed of thousands of fuzzy rules coming in the form: ifxisAk, thenyisBk. Fuzzy rules or fuzzy relations are directly related with the fuzzy sets formed in the input and output spaces, and some of the fuzzy sets appear to be of less significance in system modeling.While designing and optimizing fuzzy relation equations, it is critical for ensuring the good performance of the resulting systems such that they are endowed with high efficiency and sufficient functionality by selecting a suitable subset of fuzzy rules with high influence and removing the others from the entire rule base. In other words, fuzzy relations obtained based on the selected rules perform as efficiently as those correspond to the entire rule base. The number of rules to be selected, namely the cardinality of the subset of rules, is considered and determined in order to ensure that this subset(sample) size [23] is sufficient to obtain good performance of the simplified system.

However, it is worth noting that even though rule selection could effectively improve the efficiency and interpretability of system modeling, at the same time the accuracy of the resulting model is deteriorated to some extent because of the reduction of rules. In order to compensate for the loss of modeling accuracy caused by rule reduction, the selected(remaining) rules are made granular through allocating a certain level of information granularity. Subsequently, these granular rules give rise to granular outputs and the formed global model is referred to granular fuzzy relation model. The quality of the overall model is affected by the selected local rules and the imposed level of information granularity, and it is measured in terms of the coverage and specificity criteria of the granular results. Through determining an optimal subset of rules and a suitable level of information granularity, we arrive at a highly interpretable granular model whose accuracy and interpretability are carefully balanced and reconciled.

The motivation of this study comes with the design of a novel framework of granular fuzzy relation equations based on the optimized subsets of data, which are determined by removing those with less significant impacts using the particle swarm optimization (PSO) algorithm. As a prerequisite, rule selection is carried out for pre-determining an optimal subset as the experimental evidence for the following designing process. It is subsequently available to transform the numeric fuzzy rules (described using the selected subset of data) into interval-valued fuzzy rules (represented with upper and lower bounds), and then the interval-valued fuzzy relations are developed which are anticipated to perform as the solutions to the optimized granular fuzzy relation equations.

The originality of this study has two facets:

1) A novel framework of granular fuzzy relation equations is proposed, in which a parameterεindicating a level of information granularity is introduced to transform a suitable subset of fuzzy sets into granular (interval-valued) fuzzy sets.The granular outputs are finally obtained as the products of fuzzy sets formed in the input space and the optimized interval-valued fuzzy relations which are developed based on the selected subset of interval-valued fuzzy rules. To evaluate its performance, two conflicting criteria, coverage and specificity, are utilized such that a sound compromise between the interpretability and accuracy of the model is achieved.

2) To finalize the overall framework, especially that rule selection performs as an essential part of the realization of the granular model, a new encoding mechanism of PSO is designed and applied where fuzzy rules can be vectored,sorted, and further analyzed. The encoding mechanism of PSO makes up for the shortcomings of traditional optimization methods that are commonly encountered in feature selection[24], [25] and is designed for dealing with such discrete problems where a subset containing a certain number of rules is selected. An exploration operator is also included in PSO by extending the diversity of solutions, which reduces the computing overhead of the optimization process.

This study is structured as follows. A literature review is provided in Section II. In Section III, we present a novel framework of developing granular fuzzy relation equations by introducing a parameterεthat indicates a level of information granularity. Section IV starts with a brief introduction to the PSO and binary PSO. Then, an augmented encoding mechanism of PSO is developed to be appropriate for solving discrete problems. An exploration operator is also considered in PSO which helps improve its efficiency. Experimental studies are conducted in Section V and the conclusions are drawn in Section VI.

II. LITERATURE REVIEw

In this section, we present a brief review which consists of the basic concepts of fuzzy relation equations, granular computing and granular system modeling, and feature selection. The related works perform as essential prerequisites in the proposed scheme for realizing granular fuzzy relation equations.

A. Fuzzy Relation Equations

Fuzzy relation equations constitute important parts in fuzzy system modeling, and there are a series of related studies on the solutions to fuzzy relation equations [26]–[31]. In [18], the max-min composition is firstly introduced by Sanchez.Pedrycz [19] focuses on the fuzzy relation equations based on a max-product composition. Max-min and max-product compositions are regarded as the commonly usedt-norms in fuzzy relations. Wu and Guu [20] consider a necessary condition of fuzzy relation equations with the max-product composition. They extend this necessary condition to the situation with max-Archimedean triangular-norm composition, and then propose rules to reduce the problem’s size.Yanget al. [21] propose a method of developing addition-min fuzzy relation inequalities with application in the BitTorrentlike peer-to-peer file-sharing system.

In addition, a series of studies have been conducted on the development and optimization of fuzzy relation equations and inequalities. Loetamonphong and Fang [32] consider an optimization problem with a linear objective function subject to a system of fuzzy relation equations using max-product composition. An optimization model with a linear objective function subject to max-tfuzzy relation equations as constraints is presented by Thaparet al. [33], wheretis an Archimedeant-norm. Ghodousian [34] investigates an optimization problem of a linear objective function with fuzzy relational inequality constraints, and the feasible region is formed by the intersection of two inequality fuzzy systems and Dubois-Prade family oft-norms that are considered as fuzzy composition. Ghodousianet al. [35] study a nonlinear optimization problem with a system of fuzzy relational equations as its constraints. In order to avoid network congestion and improve the stability of data transmission, a min-max programming problem subject to addition-min fuzzy relation inequalities is proposed by Yanget al. [36]. Caoet al.[37] extend the fuzzy relational compositions based on generalized quantifiers.

Previous research endeavor to develop fuzzy relations by exploring various forms of fuzzy operations. It is still facing great challenges to improve performance in system modeling.

B. Granular Computing and Granular System Modeling

With the rapid improvement of the diversity and complexity of information, it becomes significantly challenging for describing and analyzing a large number of data using numeric models [8], [38]. It is worth noting that granular computing (GrC), which stems from the fuzzy theory proposed by Zadeh [11], [12], has become a novel and promising framework for data description and system modeling. It promotes a commonly encountered situation that data should be represented at different levels of abstraction.

Information granules [7]–[9], as well as granular models[39], are expressed in terms of various formalisms and subsequently utilized in several areas of applications.Different from the well-known numeric models, granular models are developed on a basis of information granules. As a consequence, the results produced by granular models are also information granules rather than numeric values. To be more specific, the antecedent and consequent parts of fuzzy rules are characterized by a collection of information granules,which leads to a general concept of granular fuzzy rule-based systems. Theith rule performs as follows:

By stressing the relationships between the antecedent and consequent parts of fuzzy rule-based system, the underlying architecture of granular fuzzy relation equations could be adapted by changing the level of abstraction flexibly. It is worth noting that granular models contribute to improving the performance, which is strongly influenced by the allocation of information granularity [2].

C. Feature Selection

Fuzzy relation is fundamentally generalized based on a collection of fuzzy rules, and each rule varies with respect to its level of influence. Feature selection has attracted much attention in the field of fuzzy relational modeling [40]. An iterative method to select suitable features in an industrial pattern recognition context is proposed in [41], which combines a global method of feature selection and a fuzzy linguistic rule classifier. Post-processing methods of sample size in rule selection are initially proposed by Alcaláet al. [42], considering both the rule selection and the tuning of membership functions to obtain solutions with the smallest sample size but high accuracy. Zhouet al. [43] point out that it is essential to reduce the number of rules as well as ensuring the remaining system’s approximation performance. From this brief review, we can see that selecting a suitable subset of rules is important for developing fuzzy relation equations with a higher level of performance.

In this study, we aim to explore a new way of developing granular fuzzy relation equations with high efficiency and sufficient functionality, in which the granular fuzzy relation is formed based on a subset of fuzzy rules.

III. GRANULAR FUZZY RELATION EQUATIONS BASED ON A SUbSET OF DATA

The overall conceptual framework is displayed in Fig. 1.

Fig. 1. The development framework of granular fuzzy relation by selecting a subset of fuzzy rules.

whereincl() is a binary predicate,

It is worth noting that in (14)–(17), the coverage is determined between the entire rule base and the obtained granular output, while the specificity is calculated with the use of the interval-valued outputB～k(obtained by extracting the max-min composition between the original input fuzzy setsAkand the interval-valued fuzzy relationR～).

The development of granular fuzzy relation equations is associated with a large number of fuzzy rules containing those with less important impacts which increase the computational complexity of the model. In order to make the model to be more efficient and offer sufficient functionality, determining an optimal subset of fuzzy rules is a prerequisite to developing granular fuzzy relation equations. Rule selection is realized using an augmented optimization method — an encoding mechanism of PSO, which will be discussed in the following section.

IV. DETERMINATION OF THE OPTIMAL SUbSET OF FUZZY RULES USING THE PSO ALGORITHM

Even though rule selection can help remove the rules with less important influence, it is difficult to determine which rules should be selected in order to realize an optimal fuzzy relation. Several optimization algorithms are commonly studied. Because of its powerful ability in searching for the best solution as well as the characteristic of a simple configuration, PSO [44] is widely applied to obtain a group of feasible solutions in a continuous search space. It simulates the social behavior of birds’ searching food process in a multidimensional search space [24], which aims to find out the optimal solution according to the best positions and the global best positions of each individual bird of the group. To deal with discrete problems, such as feature selection [24],Kennedy and Eberhart [45] propose the binary PSO in which the particles update their positions according to binary vectors determined by a probability defined with the velocity. A mutation operator is included in the binary PSO to improve the diversity of the solutions without compromising the solution quality [46].

A. PSO and Binary PSO as a Preliminary

The PSO algorithm [47], [48] is a population-based searching process, in which the optimal solutions are obtained iteratively. Each particle updates its velocityvi jand positionxijas follows:

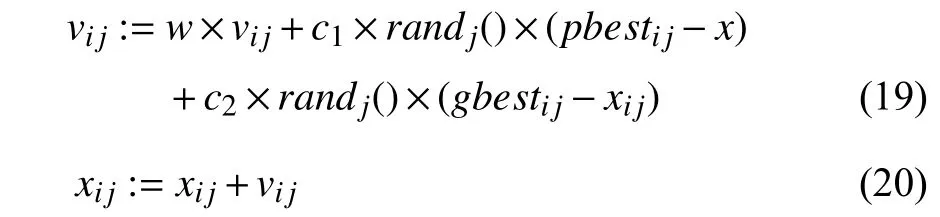
wherei= 1, 2 ,...,p, andpis the number of particles (p= 20).j= 1, 2 ,...,dim,anddimis the dimension of the experimental data;wis an inertia weight;pbestijis the best position of thejth coordinate with respect to theith particle experienced so far, andgbestijis the best position of thejth coordinate with respect to theith particle compared with the whole swarm of particles;randj() returns a random value located in the range of [0,1];c1,c2are learning factors that assume to be positive values.

The binary PSO algorithm [45] is regarded as a modified version of PSO by extending the continuous search space into binary spaces. The velocityvi jis updated in the same way as in the traditional PSO algorithm.

The positionxijis updated according to a probability value returned by a sigmoid function with respect to the velocityvij

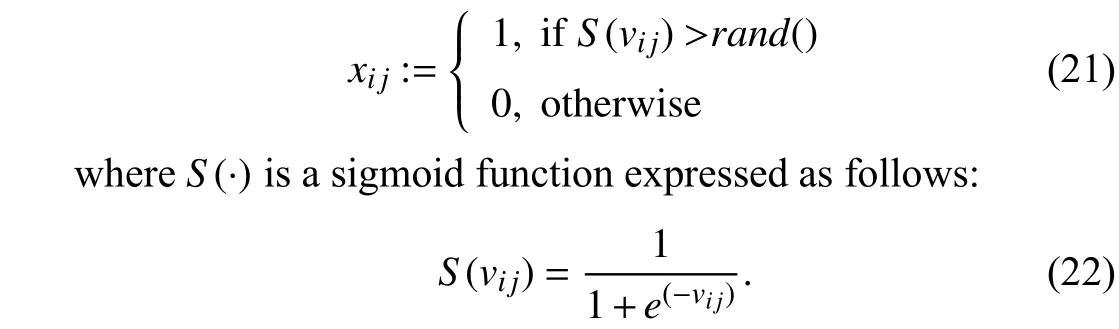
It is indicated that binary PSO updates the positionxijdepending on the value ofS(vi j), resulting in a great possibility of local convergence in which the solutions will be explored in limited local areas (the values ofxijalways remain equal to 1). The value ofS(vi j) will be approximately equal to 1 if the velocity assumes high values. In this case, a mutation operator [46], [49] is introduced to the binary PSO algorithm, which helps improve the diversity of the solutions.The mutation operator is defined as

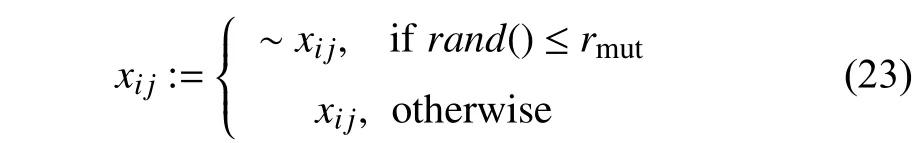
wherermutdenotes a mutation probability, which is determined with a random value distributed in [0, 1].

B. Encoding Mechanism of PSO for Selecting a Subset of Data

In this study, rule selection (selecting an optimal subset of rules with a certain number) should be regarded as a discrete optimization problem in which the positionsxijand velocitiesvijare expressed as certain integers. Since the positionsxijrepresent a collection of indices for the selected subset of rules,xijshould be determined as integers within [1,N].Meanwhile, the velocitiesvi jmean the length of steps according to whichxijare updated in each generation.vijare integers that change within [1,N], and they are required to satisfy the constraint that 1 ≤(xij+vij)≤N.

Even though the binary PSO is a considerable alternative to solve discrete problems, it can only be applied to determine whether a given fuzzy rule is selected or not. In order to select a subset of rules with certain sample size, an encoding mechanism of PSO is developed by extending the continuous search space to discrete search space.

Let us consider a rule base with a size ofN,as shown in Fig. 2.Each rule is randomly assigned with a coordinate of a vector[a1,a2, …,aM, …,ai, …,aN],ai= [ai j] ∈ [0,1]n. The selected subset of fuzzy rules is regarded as the solutions to the discrete optimization problems, i.e.,xij=ai j,i= 1, 2, …,N,j= 1, 2, …,n. The search space and the solutions corresponding to the entire fuzzy rule base are displayed in Fig. 2.

Fig. 2. Search space (rule base) and solutions (selected rules).

Fig. 3. Solutions (selected subset of rules) of encoding mechanism in PSO within discrete search space.

C. PSO With an Exploration Operator

The encoding mechanism of PSO provides a practicable way of rule selection in the proposed framework. However, a commonly encountered situation comes with that the optimal solution may be missed when the particles move too fast (the velocityvijis greater than what is expected), resulting in reduced efficiency. Inspired by the general idea of mutation operator in binary PSO, an exploration operator is included to help improve the efficiency by exploring a wider diversity of solutions, which is expressed as follows:

whererepris defined as the exploration probability,

V. OPTIMIZATION OF GRANULAR FUZZY RELATION EQUATIONS bY SELECTING A SUbSET OF DATA

To complete the framework of developing granular fuzzy relation equations illustrated in Fig. 1, PSO algorithms(including the encoding mechanism of PSO and PSO with an exploration operator) are enrolled in a multi-objective optimization problem that a subset of data and a parameter of information granularityεare optimized at the same time. The process is presented in Algorithm 1.

Algorithm 1. Optimization of granular fuzzy relation equations Initialization: randomly select M rules, M/N [1%, 100%]), =2.0.Optimization:for M/N = 1% to 100%begin Step 1: the interval-valued fuzzy relation r-ij=maxp=1,2,...,M[min(a-pi,b-pj)]∈vij r+ij=maxp=1,2,...,M[min(a+pi,b+pj)]～R=[r-ij,r+i j]Step 2: the interval-valued output b-k j=maxi=1,2,...,n[min(a-ki,r-ij)]b+k j=maxi=1,2,...,n[min(a+ki,r+ij)]～Bk=[b-k j,b+k j]Step 3: update the position (index of the selected subset rules)xij=■■■■■■■xij+vij·repr, if repr=1 xij, otherwise with an exploration probability repr=■■■■■■■1, if S(vij)＞rand()0, otherwise Step 4: mark the particles whose positions do not change as“no update”Step 5: update the positions of the particles which are marked by “no update”Step 6: fitness function cov= 1 N∑m∑m·N k=1j=1 incl{bk j,[b-k j,b+k j]}sp= 1 N∑m∑m·N k=1j=1(1-|b-k j-b+k j|)V(ε)=cov*sp end～Ropt the optimal fuzzy relation corresponds to the maximal fitness function～B= ～A° ～Ropt the granular fuzzy relation equations

It is shown that a granular fuzzy relation equation is obtained with the interval-valued fuzzy relation that is determined based on a selected subset of fuzzy rules while an encoding mechanism of PSO/PSO with an exploration operator is applied to select an optimal sample size.

VI. EXPERIMENTAL STUDIES

The main objective of the experiments is to quantify the performance of the granular fuzzy relation equations obtained based on a subset of fuzzy rules with a certain number. The selection is realized with the use of the encoding mechanism of PSO. Synthetic data as well as the publicly available UCI machine learning data sets are used in the experiments. The cardinality of the search space is equal to the number of indices within the rule base. Fuzzy sets are represented with membership grades in the range of [0, 1]. The positionsxijare initialized with the randomly selectedMrules, and the velocity is initialized asvij= 2.0. In PSO, the inertia weightw= 2.0 and the learning factorsc1=c2= 2.05.

To carry out the experiments, the size of the selected subsetMshould be neither too large in order to control the computational complexity nor too small in order to ensure sufficient functionality. Therefore, we vary the proportions ofM/Nwithin a range of reasonable values. Some comparative studies are included in this section.

A. Synthetic Data

The fitness function is described by (18). The plots of the performance indexV(ε) regarded as a function ofεare shown in Fig. 4.

Fig. 4. V(ε) as functions of ε for different sample size ratios.

Let us consider the results shown in Fig. 4, whereV(ε) is an unimodal function with a clearly visible maximum. As shown in the results, the values of performance index change as sample size ratio varies from 5% to 20%. When the sample size ratio is 5%, better performance can be obtained compared with the sample size ratio of 10%–20%. However, when the sample size ratio is increased to 20%, lower performance values are obtained when the sameεis used. As the computational complexity increases with a larger sample size,5% is the optimal solution to fuzzy rule selection to ensure a balance between a good performance and a minimal computational complexity.

When applying PSO to rule selection, we are interested in the fitness values obtained in successive generations. The results are displayed in Fig. 5.

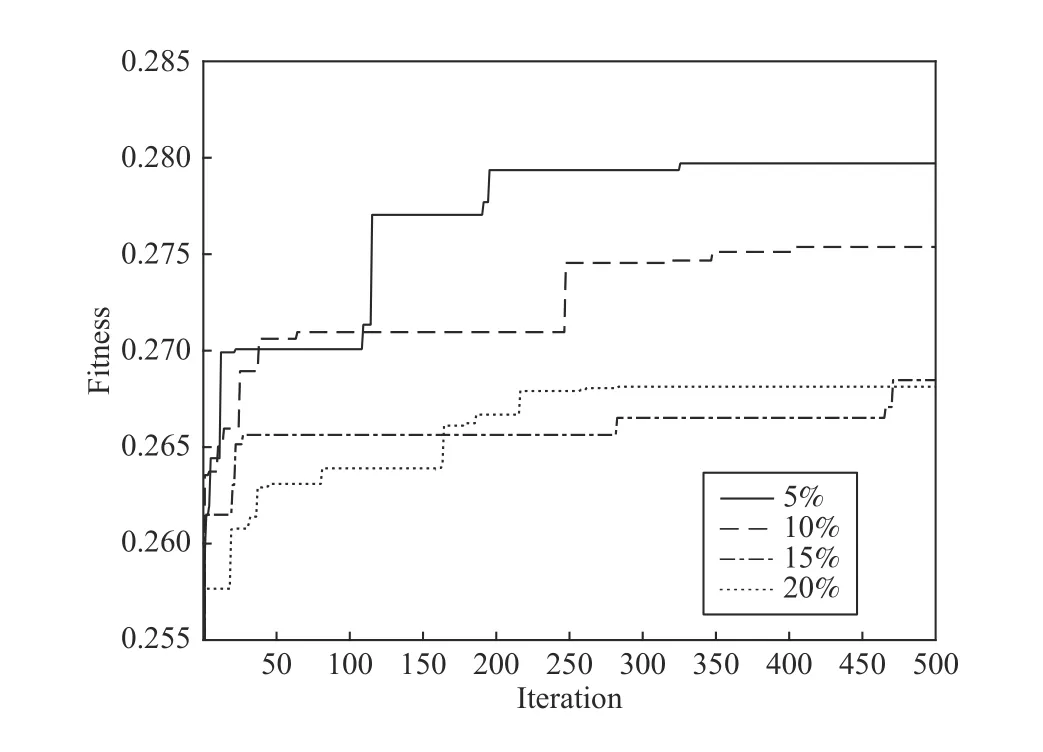
Fig. 5. Performance index with successive generations using PSO with different sample size ratios.

The results shown in Fig. 5 provide a different perspective to analyze the performance of granular outputs. It is shown that higher fitness values correspond to a smaller sample size.Consider four options in which the ratio of selected rules over the rule base is 5%, 10%, 15%, and 20%, respectively, the best performance is obtained when the sample size ratio is 5%, and the optimal values of fitness decrease as the sample size ratio increases from 5% to 20%.

The feasibility of the proposed method is verified to be functional when selecting a subset of fuzzy rules. A series of experiments are also carried out based on a collection of UCI data sets.

B. Experiments Using Machine Learning Data Sets

We consider a collection of data sets from the UCI machine learning repository (http://arhieve.ics.uci.edu/ml), and the detailed information of the data sets is presented in Table I.

The data sets come with input and output variables (xk,yk),k= 1, 2, …,N, and can be transformed into fuzzy sets of input and output spaces (Ai(xk)) , (Bj(yk)),i= 1, 2, …,q1,j= 1,2, …,q2,q1= 5,q2= 3. The fuzzy setsAi(xk) andBj(yk) are represented by the corresponding variables of the input and output data following the standard Fuzzy C-Means (FCM)formulas.

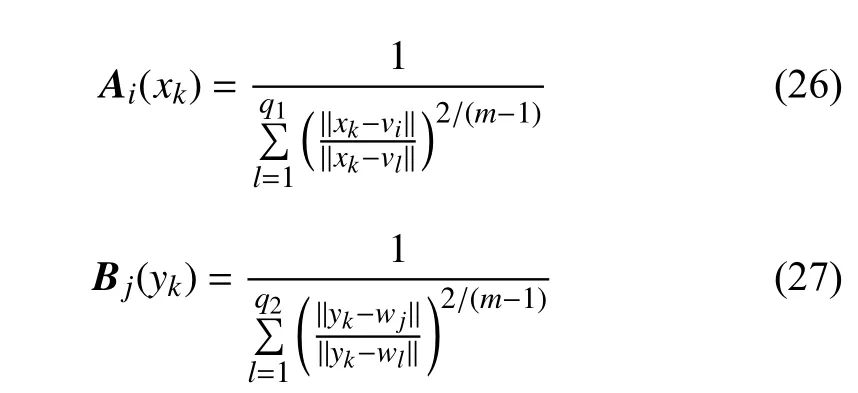
whereviandwjare the prototypes located in the input and output spaces, respectively.mis the fuzzification coefficient,and usuallym= 2.0.

First of all, it is essential to verify the feasibility of the proposed model in developing granular fuzzy relation equations based on a subset of data that is decided through rule selection. As a prerequisite, we are interested in selecting a certain number of fuzzy rules from the entire rule base. One feasible alternative is selecting rules one by one randomly,which means that one more rule is selected at each time until all the rules in the rule base are selected. The sample size of the selected rules ranges from 1 toN, in other words, the value ofM/Nchanges from 0% to 100%. In order to finalize the rule selection, two different methods are applied to the selection process: 1) rule selection realized without using any optimization methods, that is, rules are selected in sequence one by one randomly; 2) selecting one more rule each generation until a suitable subset of fuzzy rules is selected with the use of PSO. To process with selection using PSO,certain sample sizes from 1 toNare expected to be selected,and the experiments are also performed by selecting rules randomly for comparison. The selection is repeated at least 10 times and the average results are reported.

In Fig. 6, we show the performance of rule selection in terms of the performance index obtained with the use of PSO compared with that without using PSO.

The results shown in Fig. 6 indicate that for each data set,the performances of granular fuzzy relation equations obtained with the use of PSO are better than those without using PSO. With respect to the size of the selected rules, the optimal performance is obtained when the ratioM/Nis in the range of 30%–50%. It is noted that the way of selecting rules one by one provides a reasonable solution to rule selection,but it is not a good idea regarding to its high computational complexity.

For comparative analysis, we consider that a subset of rules is selected by using PSO in two different ways. One case is to select by index in which a certain number of fuzzy rules are randomly selected with respect to their index; in the other case, rule selection is processed by carrying out the proposed framework as described in Section III. An encoding mechanism of PSO is applied to both of the two cases.

The results of the two cases are presented in Fig. 7. Fig. 7 plots the performances of the proposed model as well as selecting a subset of data by index. The sample size increases from 1 toN. The performance is greatly improved when rules are selected with the proposed framework compared to that selected by index. The corresponding sample ratios for obtaining an optimal performance are in the range of 30%–50%.

We are also very interested in the comparative analysis between the results shown in Figs. 6 and 7. It is shown that the PSO algorithm can definitely improve the performance of the rule selection and the proposed framework indicates a better feasibility in selecting a suitable subset of rules to obtain the optimal granular fuzzy relation equations. It provides a general idea of optimizing granular fuzzy relation equations by introducing the encoding mechanism of the PSO algorithm to the proposed framework in this study.

In Table II, we present a summary of the optimal performance valuesV(ε) with their corresponding values ofεfor a collection of UCI data sets. In the table,Nstands for the size of the rule base, and the sample ratios are considered asM/N= 25%, 30%, and 35%, respectively. The performance values obtained by selecting using PSO and selecting without using PSO are the same as shown in Table II.

Through conducting the optimization problem using PSO, a subset of fuzzy rules and an optimal value of parameterεcan be determined, which are subsequently utilized to the development of granular fuzzy relation equations followingthe formulas presented in Section III.

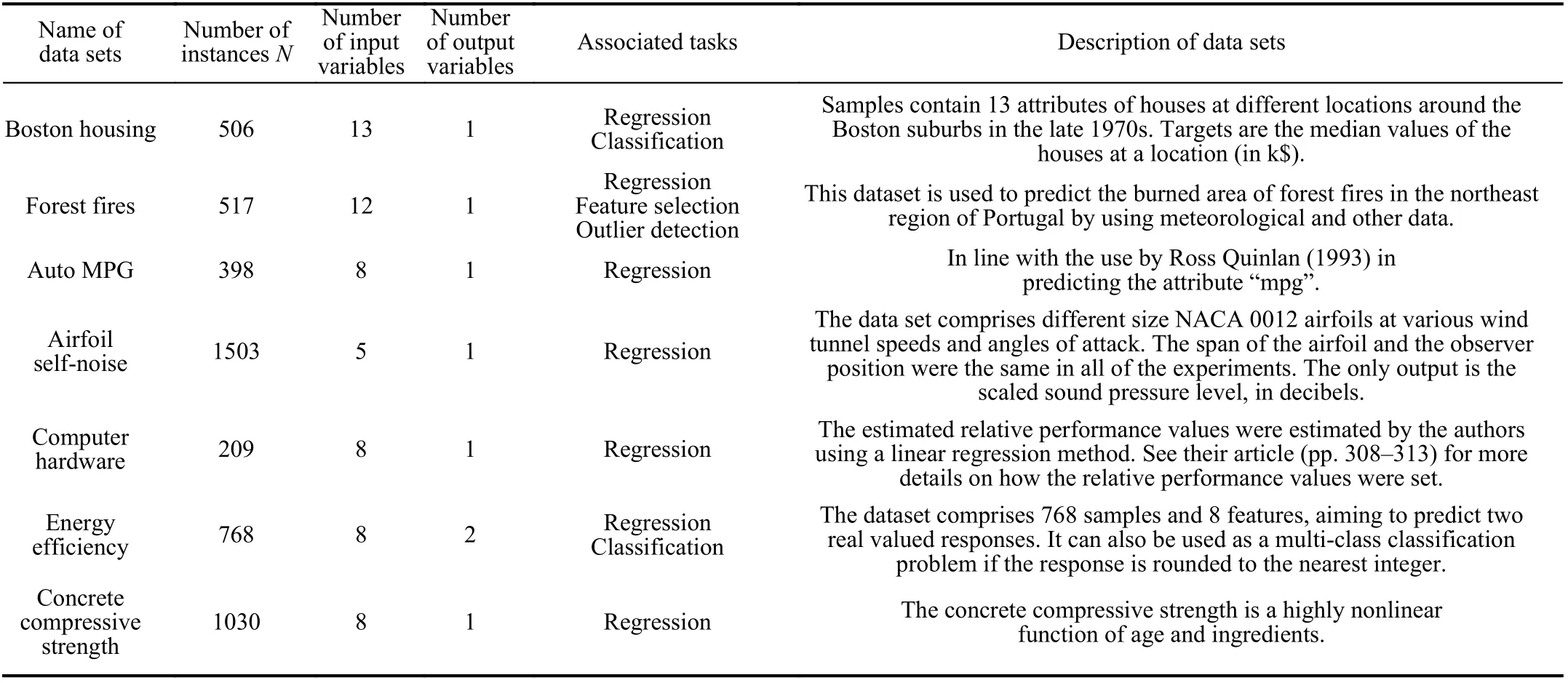
TABLE I DETAILED INFORMATION OF DATA SETS USED IN THE EXPERIMENTS

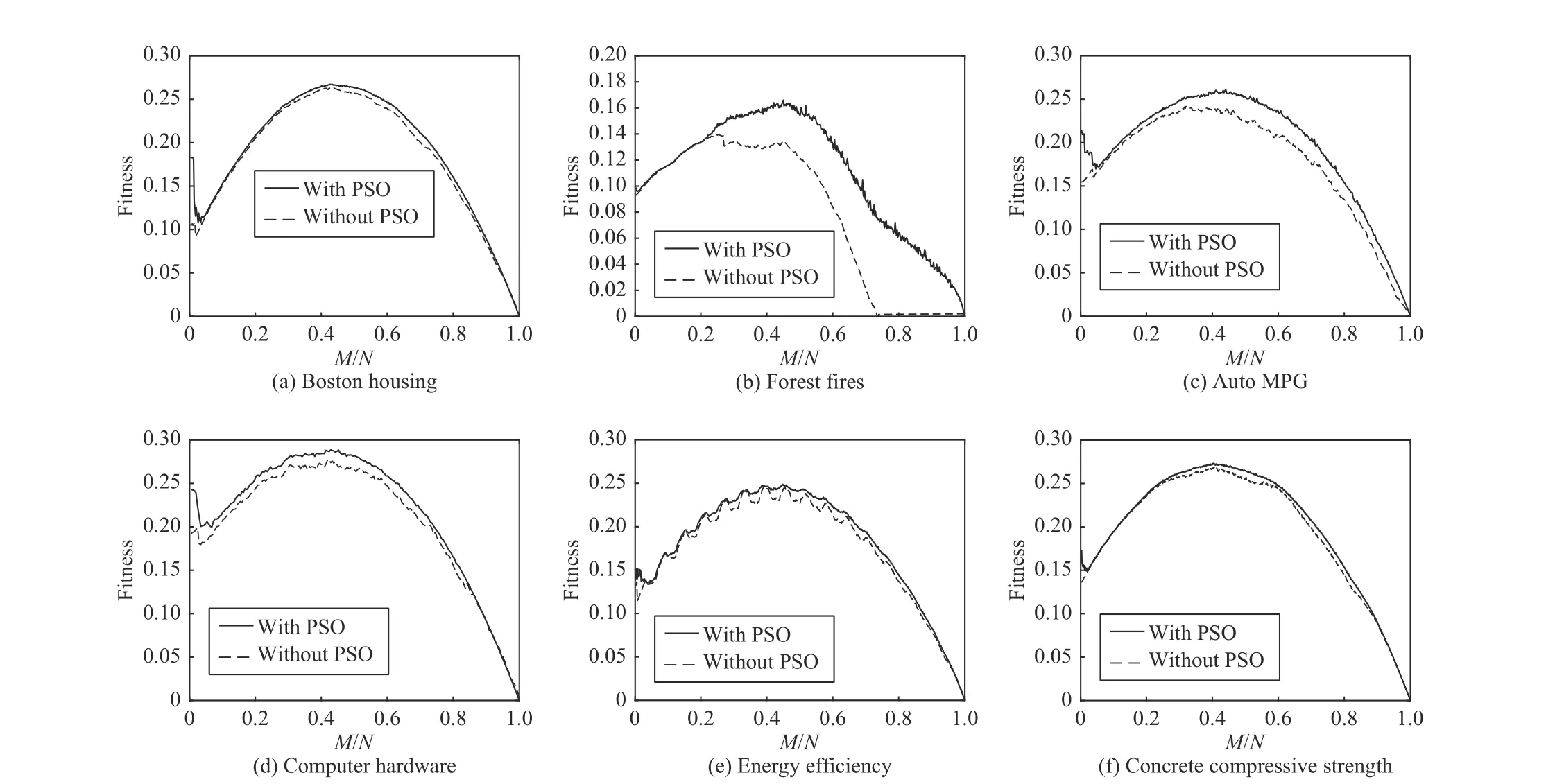
Fig. 6. Plots of performance index with the use of PSO and without using PSO.

To further improve its efficiency, we consider extending the diversity of solutions by including an exploration operator to PSO. In Table III, we present the computing overhead for obtaining the expected optimal performance values by using the encoding mechanism of PSO, PSO with an exploration operator, and selecting without PSO. The experiments are repeated 10 times, and the average values are reported. The results shown in Table III indicate that both of the two methods — the encoding mechanism of PSO and PSO with an exploration operator, can be used for rule selection with a high level of efficiency. The computing overhead is directly dependent on the distribution of data set. It can be concluded that great improvements are achieved when using PSO compared with random selection performed without using PSO. To be more specific, the exploration operator helps PSO to improve its efficiency by extending the diversity of solutions. By carrying out PSO with an exploration operator,the largest improvement achieved is equal to 98.21% (for the Forest fires data set) while the least improvement is achieved to 61.31% (for the Concrete compressive strength data set),and the average improvement attained is about 90.42%. As for processing rule selection with the encoding mechanism of PSO, the largest improvement achieved is equal to 97.28%(for the Airfoil data set) and the least improvement is achieved to 31.16% (for the Boston housing data set), and an average improvement is obtained as about 78.56%. Among all the data sets used in the experimental studies, the best improvement is obtained for the Airfoil data set for both the two methods.

Fig. 7. Plots of performance index with the use of PSO.

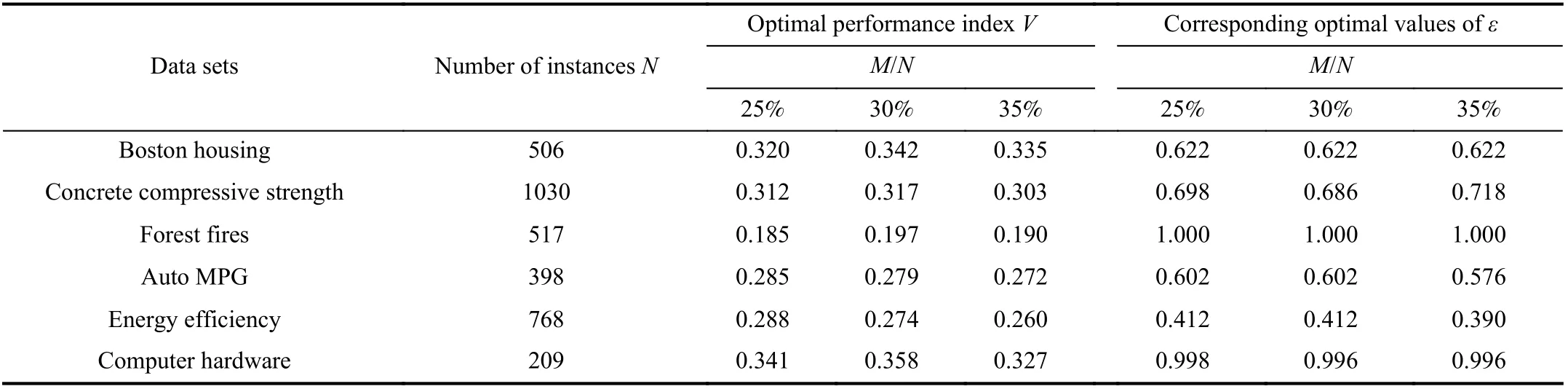
TABLE II PERFORMANCE V(ε) FOR SELECTED VALUES OF ε

We compare the computing overhead in processing rule selection by using PSO and PSO with an exploration operator.It is found that it takes less time for the later one — PSO with an exploration operator to obtain an optimal performance index. The exploration operator can help reduce the cost of time with the best improvement as large as 58.46% (for Boston housing data set), and an average improvement is about 11.88%.

It is worth noting that different efficiency improvements are obtained based on different data sets. However, it is obvious that both the encoding mechanism of PSO and PSO with an exploration operator are beneficial in rule selection, which can be used to finalize the development of granular fuzzy relation equations in this study.

VII. CONCLUSIONS

The development of fuzzy relation equations is both critical and challenging in fuzzy system modeling. In this study, a framework of granular fuzzy relation equations is proposed, of which the efficiency is maximized while the functionality is ensured. To reduce computational complexity with limited processing resources, it is essential to develop fuzzy relations by evaluating and selecting an optimal subset of fuzzy rules.The encoding mechanism of PSO is introduced to rule selection, and an exploration operator is also included in PSO to extend the diversity of its solutions.

To verify the feasibility of the proposed framework, a series of comparative experiments are studied. First of all, rule selection is carried out by selecting rules one by one randomly from the rule base. It is convinced by the results that the PSO algorithm can help in improving the efficiency of the framework. To finalize the development of granular fuzzy relation equations, we also consider selecting fuzzy rules following two methods: one is about selecting by index while the other one is processed with the proposed framework, inwhich a subset of fuzzy rules are selected and subsequently they are transformed to interval-valued fuzzy rules by introducing a level of information granularity. Synthetic data as well as a collection of UCI data sets are enrolled in the experiments. It is indicated from the results that the optimal sample ratios are 30%–50%. Finally, the granular intervalvalued fuzzy relationR～ can be determined based on the optimal subset of fuzzy rules and the corresponding optimal value ofεfollowing the processes in Section III.

TABLE IIICOMPUTING OVERHEAD

The ultimate objective of this study is to establish and optimize granular fuzzy relation equations by achieving high efficiency and maintaining sufficient interpretability. Future directions can be conducted in the following ways. First, it is of great interest to introduce various forms of fuzzy operations into the development of granular interval-valued fuzzy relations. Second, the sample size of the optimized subset of fuzzy rules is not confined to a static value, and it can be a complex matrix or a correlative function obtained from other downstream systems. Finally, granular fuzzy system modeling can be greatly enhanced from the processing efficiency side which is worth exploring in further research.