该如何用电像法处理导体球腔

姜志锋

(鄱阳县第一中学 江西 上饶 333100)

黄亦斌

(江西师范大学理学院 江西 南昌 330000)

1 电像法概述

电像法是处理导体静电感应问题的利器.其基本思路是：对于所研究的区域,内部有点电荷，边界为导体,如图1(a)所示，希望能找到仅由点电荷组成的体系，如图1(b)所示，使得所研究区域内的电场与后一情形下对应区域内的电场完全相同.此时，新引入的电荷称为像电荷.

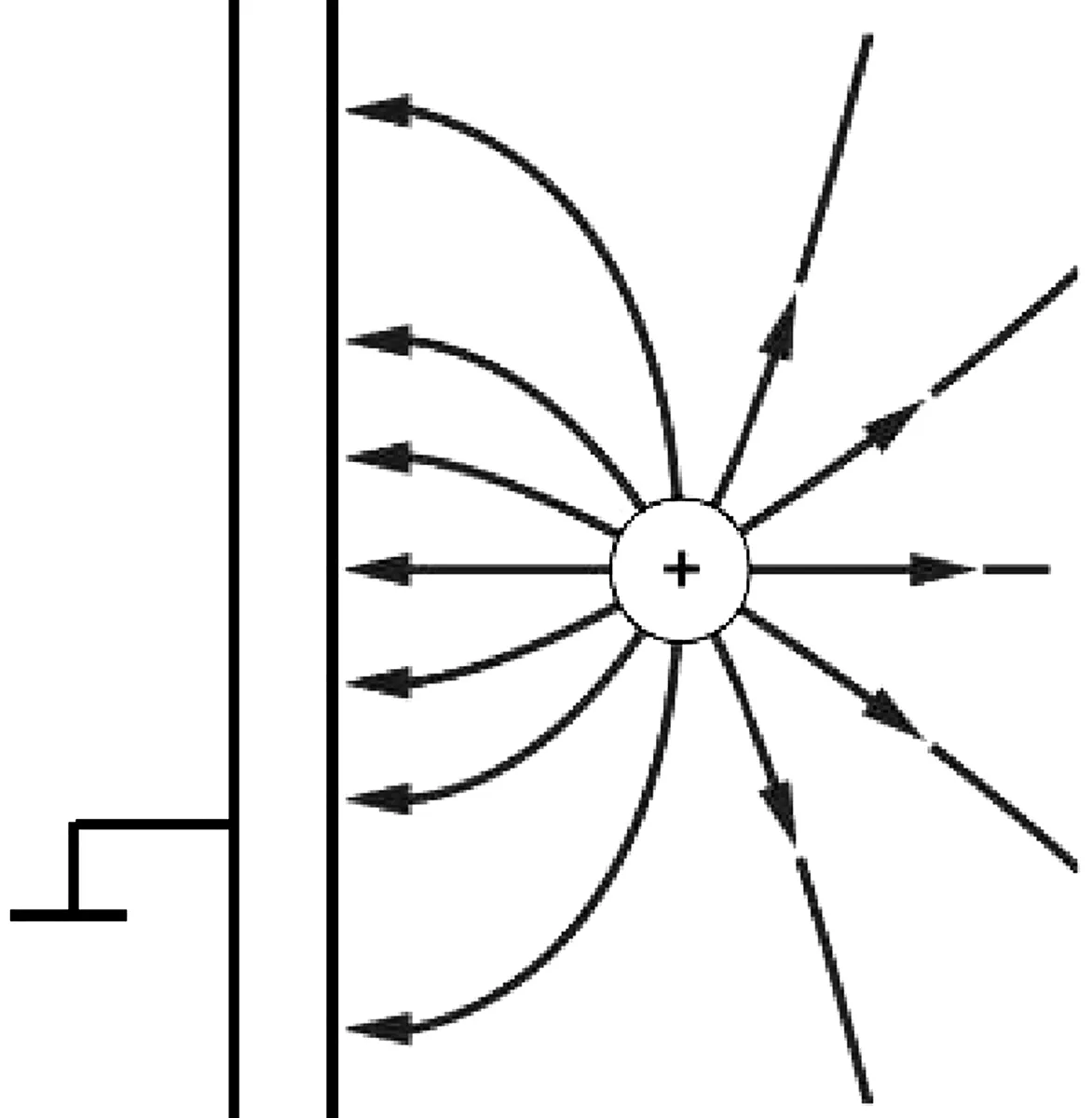
(a)研究区域内有点电荷，以接地导体平板为界

那么，目标能否实现呢？有唯一性定理支持.唯一性定理指出:对于一个区域，如果给定内部的电荷分布，又给定边界条件，那么区域内的电场被唯一确定.据此，如果有两个相同的区域，只要内部电荷分布相同，且边界条件相同，则两区域内的场强分布相同.

什么是“给定边界条件”呢？对于以导体为边界的情况，常见情形包括：给定各导体电势；给定各导体电荷量；给定部分导体的电势和其他导体的电荷量.要注意，无法对同一个导体同时任意给定其电势和电荷量.一般来说，对这种边界条件，体系是无解的.

如果用唯一性定理解决静电感应问题，那么，首先，要注意所引入的像电荷必须处在所研究区域之外，否则就改变了区域内的电荷分布.然后，要利用经验和推理，研究在区域外怎样的点电荷分布(连同区域内已知的电荷分布)可以实现所需的边界条件.

接地导体球的静电感应是一个经典问题.通常的做法是，假定球内部有一点电荷，设定其电荷量和位置，要求其与球外电荷一起使得球面的电势为零.研究发现，这一要求可以得到满足，且有唯一解，于是我们就找到了镜像电荷的电荷量和位置[1]

(1)

其中，各字母的意义和所求电场如图2所示.(图示默认q为正电荷，q′为负电荷，若电性相反，则电场线方向相反)

另一条思路是：首先可以证明，不等量异号电荷系统，一定存在唯一一个等势面是球面，如图3中的虚线，而且其电势为零，其几何性质(球心位置、半径)由两电荷的电荷量和位置确定.于是，可以将导体球面与该等势球面等同，从而反向推出镜像电荷的位置和大小.图2和图3两图在球外空间的电场就完全相同.

图2 点电荷与接地导体球之间的电场

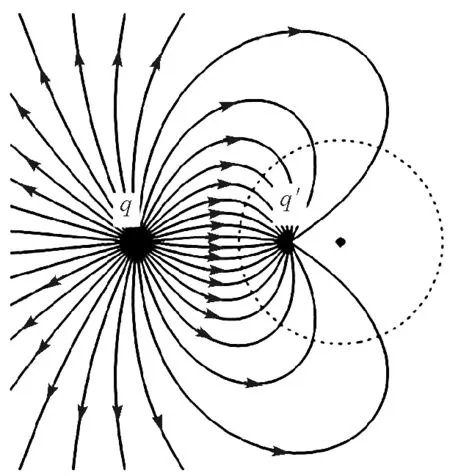
图3 不等量异号电荷间的电场(图中虚线表示球面等势面)

一个值得注意的结论是：导体球表面的总感应电荷正好等于镜像电荷.这一点可以用高斯定理证明.

2 导体球腔情形

如果是导体球腔内偏心b处置一点电荷q′,该如何用电像法求解腔内的电场？

实际上，图3已经给出了答案：其虚线内的电场即为所求.将其重画为图4.此时，像电荷q的数值与离球心的距离d仍由式(1)给出.此时，腔内任一点的场强就等于电荷q′与像电荷q在这一点产生的场强，腔内表面的电荷在腔内的作用可以用腔外的点电荷q来代替.问题就这么简单地解决.

图4 导体球腔的电像法示意图

但是跟导体球外情形对比时，有几个问题值得澄清.首先，此处球腔内表面的总感应电荷量(-q′)显然不等于像电荷的电荷量q，而且显然|q|>|-q′|，这会不会有问题？没有.因为电像法唯一需要做到的只是场强等效，而我们已经做到了.其他结论与球外情形相同或不同，都无需揪心.

其次，研究区域中某点的电势等于源电荷与像电荷在该点产生的电势之和，这一条对球外情形成立，但对球腔内情形就不能再这么说了.原因在于：谈论“电势”时，我们一般默认无穷远处为电势零点；而“无穷远处”在球外情形属于研究区域内，而在球腔内情形则不属于.实际上，不论是哪种情形，我们能得到的，只是研究区域内的电场，从而只能得到研究区域内任意两点的电势差.球外情形之所以可以谈“电势”，仅仅是因为电势零点幸运地处于该区域中，故而“电势差”变成了“电势”.球腔内情形则没有这种幸运，从而只能说：腔内某两点的电势差等于源电荷与像电荷在该两点产生的电势差之和.电势叠加变成了电势差叠加.

那么，腔内某点的电势该如何确定呢？由于腔外情形未知，从无穷远处到腔内该点的场强分布未知，从而无法对腔内某点的电势分布下任何断语.如果实在要给出，那么只能是下面的形式

(2)

(3)

该式的意义非常明显.空间中任何一点的电势等于源电荷、内表面电荷以及其他电荷产生的电势之和，但如果该点在球腔内，那么内表面电荷的贡献可以用像电荷代替.

3 例题

兹以文献[2]中的一道题为例，说明上述内容.

【例题】如图5所示，一个带电荷量为q的点电荷置于内外半径分别为r1和r2、不带电导体球壳的空腔内的P点，其离球心的距离为a(a

(1)点电荷q所受的静电力；

(2)点电荷q与其他电荷之间的电势能.

图5 例题题图

解析：

(1)静电感应后，球壳内表面的电荷非均匀分布，总电荷量为-q，外表面电荷均匀分布，总电荷量为q.q所受的静电力为外表面电荷与内表面电荷所施加的力之和，其中前者为零，后者由图中像电荷q′决定[2]

于是，该力为

(4)

(5)

故

U内P还可以用另一种方式解决：先得到内表面电荷在空间中产生的电场，再通过积分得到其在P点的电势.该电场分布如图6所示，其在内表面以外产生的电场如同P点处-q产生(内表面电荷与P点的电荷q在内表面以外产生的合场强为零)，而在内表面以内产生的电场如同像电荷q′产生(注意图中的电荷-q和q′并不真实存在).为求P点的电势，场强积分路径既可以从P出发一直向右到无穷远

又可以从P点往左直到无穷远

二者的结果都与式(5)相同.

图6 内表面非均匀电荷产生的电场