地铁车车体结构性能仿真分析

许 喆，李永华，盛自强，刘东亮

（1.中国中车唐山机车车辆有限公司技术研究中心，河北 唐山 063500；2.大连交通大学a.机械工程学院；b.机车车辆工程学院，辽宁 大连 116028）

0 引言

地铁车体作为运输乘客的直接载体，车体的设计和制造水平与车辆运行舒适性和安全性有着紧密的联系[1-2]。车体结构设计的合理性是保证车辆结构安全极其重要一环，因此需要对新设计的车体结构进行性能仿真分析，以发现其设计的不合理之处，为后续结构改进和优化提供理论参考。以往对于车体的结构性能分析通常采用实车试验的方式进行，该方法费用高昂且耗时耗力，增加了车辆设计的研发成本[3]。有限元法因其对求解区域的适应性强、求解效率和精度高，在工程领域中得到了广泛的应用[4-6]。王秋实等[7]通过有限元分析技术对机车转向架的强度及模态进行了校核，得出转向架构架满足设计要求的结论。刘春艳等[8]利用有限元仿真对轨道客车的车体结构强度进行了分析，并且与试验结果作对比，发现仿真结果与试验结果十分接近，表明仿真分析可用于指导产品的研发设计。王青权等[9]以某型轨道客车的铝合金车体为研究对象，采用有限元仿真和试验相结合的方法分析了车体的静强度特性，发现车体安全系数较高存有一定的轻量化空间，此外还找出了车体应力较大的区域，为后续车辆机构设计的改进提供了依据。Dumitriu等[10]基于有限元仿真分析发现在车体底架横梁上安装抗弯连杆，可以有效提高车辆的行驶平稳性。

本文以某型地铁车车体为研究对象，基于Hy⁃permesh软件建立其有限元模型，依据EN 12663标准中P-Ⅲ车辆类型相关载荷要求确定车体各计算工况，对车体进行结构性能仿真分析。分析结果表明，根据GB/T 7928-2003《地铁车辆通用技术条件》标准，车体各项性能参数均满足设计要求。

1 地铁车车体有限元模型的建立

车体主要包括车顶、底架、侧墙、端墙和司机室，本文的研究对象为中间车车体，因此不含有司机室结构。车体主要有薄板铝合金材料焊接而成。

将车体几何模型导入Hypermesh软件中进行网格的划分。考虑到车体的结构特点和保证计算的精确性，车体的有限元模型主要以四节点薄壳单元构成，网格大小控制在30mm左右。板材之间使用梁单元模拟。划分完成后的车体有限元模型如图1所示。该有限元模型由156 127个单元，1 394 380个节点组成，车体材料的性能参数见表1。

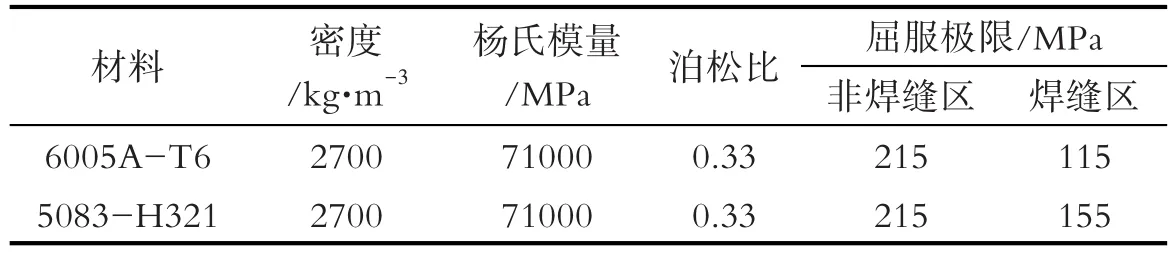
表1 材料的性能参数

图1 车体有限元模型

2 车体刚度、静强度及模态分析

2.1 确定计算工况和位移约束条件

根据EN 12663标准中P-Ⅲ车辆类型相关载荷要求确定车体静强度计算工况。选取车体超员状态垂向载荷工况，最大垂向载荷工况和二位端端墙上边梁位置150 kN压缩工况进行车体的静强度和刚度校核。在四个空气弹簧座处约束垂向位移，在两个中心销处约束横向位移，在二位端车钩座处约束纵向位移。各工况载荷及其约束条件见表2，各工况位移边界条件示意图如图2所示。

表2 计算工况列表

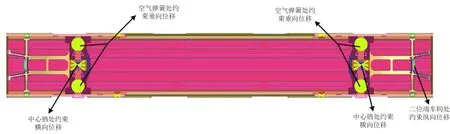
图2 车体边界约束示意图

2.2 车体刚度分析

车体在最大垂向载荷作用下，其刚度分析主要关注部位是边梁的垂向位移。根据GB/T 7928-2003《地铁车辆通用技术条件》标准要求：在最大垂向载荷作用下，车体底架边梁静挠度不超过两转向架支撑点之间距离1‰。本文所研究的车辆定距为12 600 mm，因此车辆底架边梁的垂向位移不得超过12.6 mm。有限元仿真所得边梁垂向位移云图如图3所示。由图3可知，其垂向最大位移为12.4 mm，小于设计许用值，车体刚度满足设计要求。

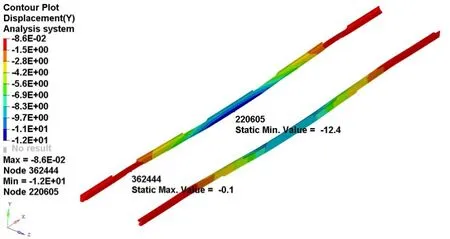
图3 最大载荷作用下车体垂向位移云图

2.3 车体静强度分析

在2.1中确定的工况下，对车体进行静强度仿真分析，计算出各工况下车体最大应力。工况1到工况3的应力云图分别如图4到图6所示。各工况最大应力出现部位、应力大小及其安全系数见表3。

图4 工况1仿真结果应力云图

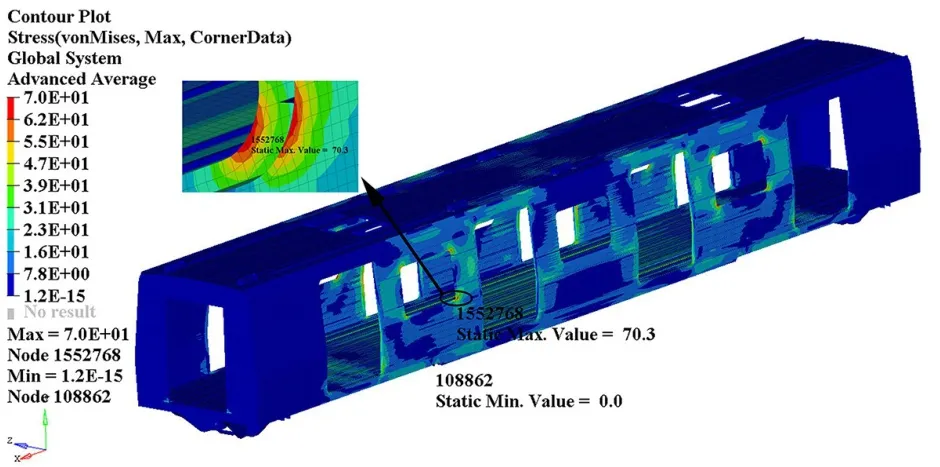
图5 工况2仿真结果应力云图

图6 工况3仿真结果应力云图

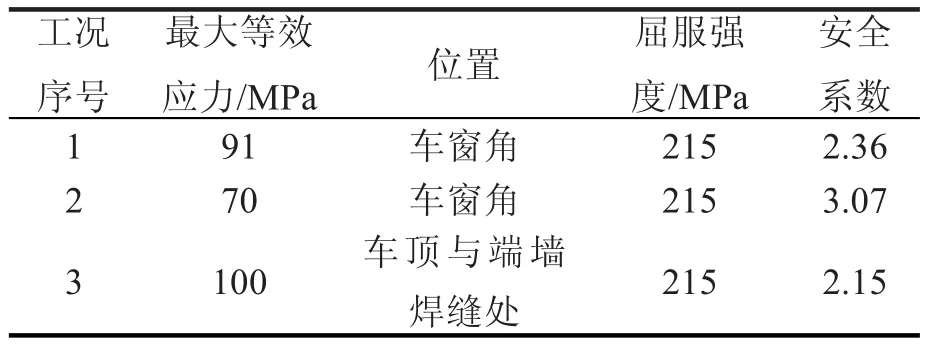
表3 各工况仿真结果的对比

通过各工况仿真分析结果可知，各工况下车体最大等效应力均小于材料屈服强度，各部位安全系数均大于1，车体静强度分析结果表明，车体结构满足设计要求。从应力云图中可知车窗角、车顶与端墙焊缝处容易产生应力集中，设计时应重点关注此部分区域。

2.4 车体模态分析

车辆行驶的安全性、可靠性和舒适性与车体自身振动特性紧密相关[11]。当车体结构的某一固有频率等于或接近外界激励频率时，车体结构将会发生共振，从而对车辆的安全性造成直接影响。因此，对新设计的车体需要通过模态分析来评估其是否会发生共振现象。

在模态计算中，对车体结构进行了自由模态分析。车体的固有频率通常有多阶，其中前6阶为刚性模态，7阶以后为弹性模态。工程实际中，通常关注的是弹性模态，因此前6阶模态本文不予考虑[12]。表4为车体7～15阶模态计算结果。对车体模态进行分析时，需要捕捉车体的一阶垂向弯曲振型和一阶扭转振型。车体一阶垂向弯曲振型云图和一阶扭转振型云图分别如图7和图8所示。

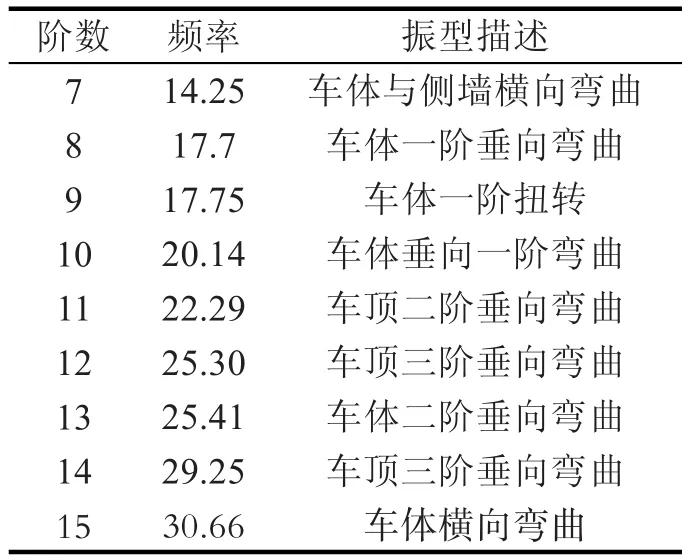
表4 车体模态分析结果

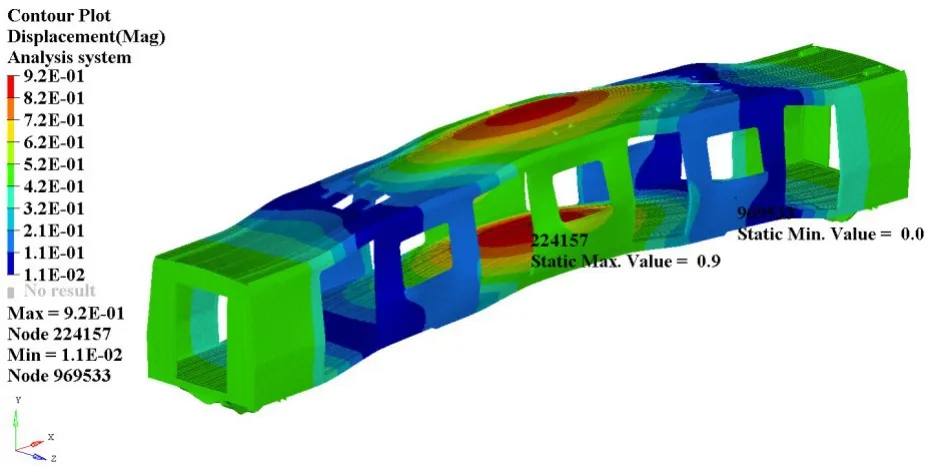
图7 一阶垂向弯曲振型云图

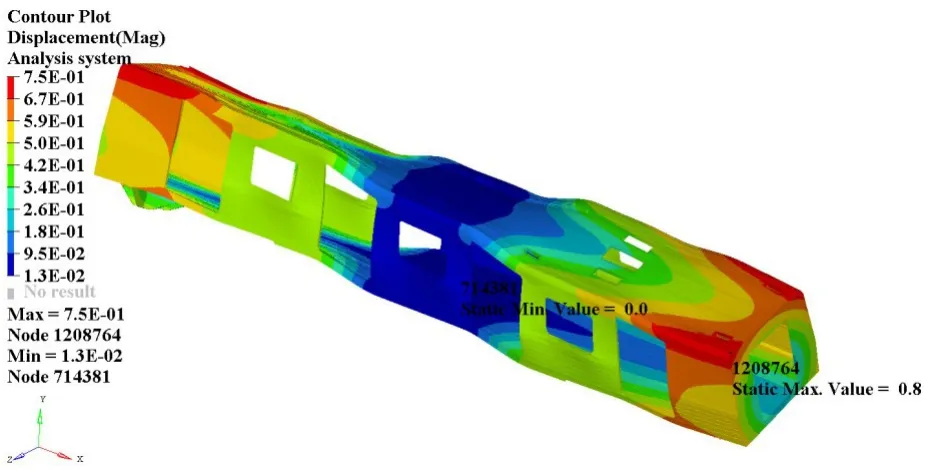
图8 一阶扭转振型云图

由车体模态计算结果可知车体结构的一阶垂向弯曲频率为17.70 Hz，一阶扭转频率为17.75 Hz，依据相关标准，转向架的垂向自振频率小于等于2 Hz。因此车体结构不会与转向架发生共振，该结构满足设计要求。

3 车体疲劳强度分析

本次疲劳强度评估方法采用疲劳极限法[13]。疲劳极限是一个应力程度，如果计算应力不超过材料的疲劳极限，在该应力程度时就不会发生疲劳损坏，也即无限寿命。首先根据EN 12663标准确定了疲劳强度计算工况，具体工况数值见表5。材料的疲劳极限图如图9所示，焊缝等级取为F。

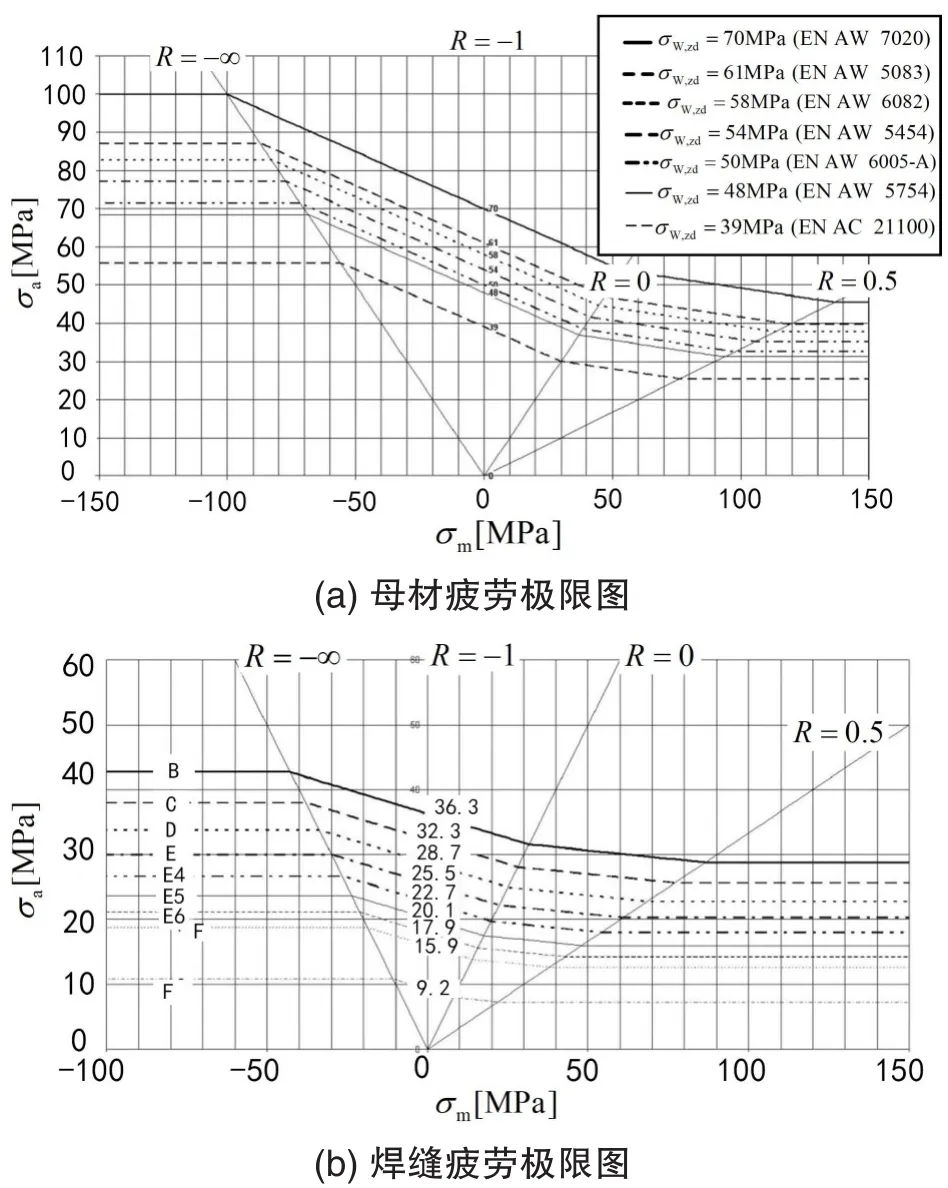
图9 材料疲劳极限图

表5 疲劳计算工况列表

表5中g为重力加速度，值为9.8 m/s2。疲劳强度的分析结果如下：

①疲劳工况1为纵向载荷工况，应力比R=-1，该工况下最大第一主应力为8 MPa，出现在车钩座处，由图9（a）可知其未超过母材的疲劳极限50 MPa，满足设计要求。疲劳工况1的应力云图如图10所示。

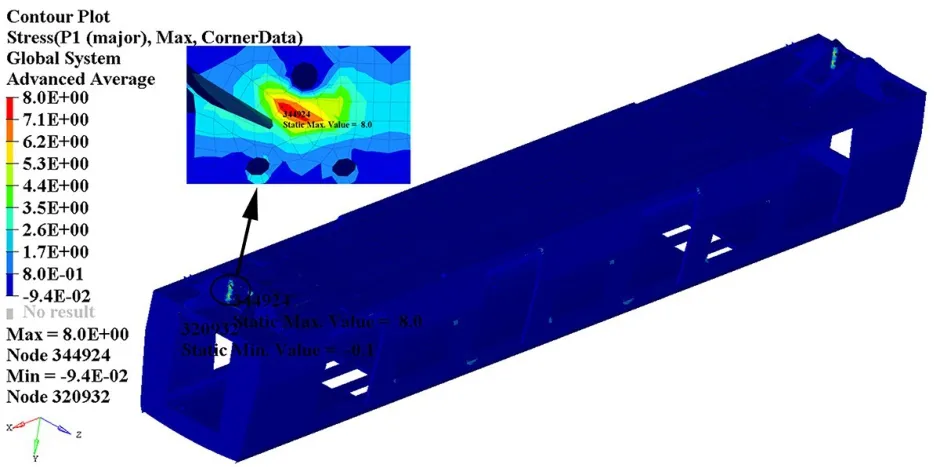
图10 疲劳工况1的应力云图

②疲劳工况2为横向载荷工况，应力比R=-1，该工况下最大第一主应力为4.9 MPa，出现在端墙门柱与底架连接处，由图9（b）可知其未超过焊缝的疲劳极限15.9 MPa。疲劳工况2的应力云图如图11所示。

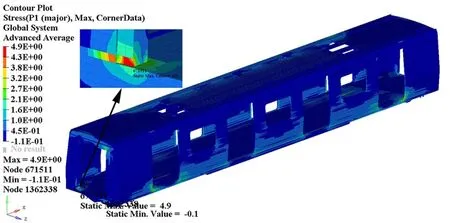
图11 疲劳工况2的应力云图

③疲劳工况3为垂向载荷工况，应力比R=0.74，该工况下最大第一主应力为2.7 MPa，发生在侧墙窗角处，由图9（a）可知其未超过母材的疲劳极限40 MPa。疲劳工况3的应力云图如图12所示。

图12 疲劳工况3的应力云图

综上所述，通过对车体进行疲劳强度分析，车体各部位在各疲劳强度工况下的最大第一主应力均未超过母材或焊缝的疲劳极限，表明该结构满足疲劳强度设计要求。

4 结论

本文以某型地铁车车体为研究对象，建立其有限元模型，基于有限元法对其刚度、静强度、模态和疲劳强度进行了校核，得出以下结论：

①车体在最大垂向载荷作用下，其底架边梁最大垂向位移12.4 mm，小于设计要求12.6 mm，满足车体的刚度设计要求。

②车体在三种静强度载荷工况下，最大等效应力均小于材料的屈服强度，且安全系数均大于1，由此可知车体满足静强度设计要求；此外，还对车体进行了模态分析，模态计算结果表明车体不会与转向架发生共振，满足设计要求。

③通过对车体的疲劳强度计算分析可知，车体各部位在各疲劳工况下的最大第一主应力均未超过母材或焊缝的疲劳极限，满足车体疲劳强度设计要求。