基于KPCA-CSO-RVM模型的工艺管道腐蚀速率预测

马梦桐，赵 琢

(1.西安石油大学石油工程学院，陕西 西安 710065；2.中海油安全技术服务有限公司,天津 300450)

对于石油化工企业而言，为了生产的需要会建设大量的工艺管道，受到工艺管道内介质、外界环境等因素的影响，工艺管道运行一定的时间后必然会出现大量的腐蚀问题。而影响工艺管道腐蚀速率的相关因素较多，且这些影响因素与工艺管道腐蚀速率之间的关系相对较为复杂，很难总结出工艺管道腐蚀速率的影响因素与腐蚀速率之间的数学关系。另一方面，工艺管道腐蚀速率的影响因素并不是一成不变的，影响因素数据无时无刻不在变化，这使得总结影响因素与腐蚀速率之间的数学关系难度增加。事实上，为了保障石油化工企业工艺管道的安全运行，研究工艺管道腐蚀速率的预测方法十分关键。

目前，国内外学者对于管道的腐蚀问题进行了大量的研究，提出了众多可用于管道腐蚀速率预测的智能算法。如程浩力等对灰色系统理论和最小二乘理论进行了全面的总结，在此基础上，使用Excel软件建立了用于油气管道腐蚀速率预测的GM(1，1)模型，并通过实例验证发现，该模型的预测精度和可靠性都相对较好，可以用于油气管道腐蚀速率的预测；Biezma等提出了一种模糊逻辑方法，使用该方法对管道的外腐蚀速率进行了预测研究，并在预测研究的过程中采用了油气管道外腐蚀速率的6项影响因素，其预测误差相对较低；许宏良等通过对管道腐蚀的机理进行深入分析，使用粒子群算法对BP神经网络算法进行了全面的优化，并使用优化后的BP神经网络算法对油气管道CO和HS的腐蚀速率进行了预测研究，结果发现该模型算法预测结果的误差可以控制在5%之内，利用该模型可以很好地对油气管道的腐蚀速率进行预测；曲志豪等对HS环境下油气管道的腐蚀机理和腐蚀产物进行了全面的研究，在此基础上，使用网格搜索算法对随机森林算法进行了优化，并使用优化后的随机森林算法对油气管道HS的腐蚀速率进行了预测研究，结果表明优化后的随机森林算法可以很好地对油气管道HS的腐蚀速率和产物类型进行预测。在相关向量机(RVM)算法的应用方面，马佳良曾使用蜂群算法对RVM算法进行了优化，并使用优化后的组合模型对原油储罐底部的腐蚀速率进行了预测，预测结果显示该组合模型与其他模型相比，其预测误差相对较小，在充分考虑影响因素的前提下可以使用该组合模型对储罐底部的腐蚀速率进行预测。在鸡群优化(CSO)算法与RVM算法的组合方面，付华等曾对两种类型智能算法的组合方法进行了全面的研究，并使用这两种算法组合后的模型对瓦斯的涌出量进行了预测，其预测精度相对较好，证明这两种算法可以进行组合使用。

通过对国内外油气管道腐蚀速率预测研究现状进行分析后发现，现有的预测方法较为单一，且在使用的过程中并没有全面考虑油气管道腐蚀的影响因素，也没有考虑众多影响因素的冗余性，这使得预测结果存在较大的误差。此外，这些预测方法在使用的过程中对数据量的要求较高，而现实中获取的油气管道腐蚀速率及其影响因素的数据十分有限。针对目前研究中存在的问题，本次提出一种基于核主成分分析(KPCA)算法、鸡群优化(CSO)算法、相关向量机(RVM)算法组合模型的工艺管道腐蚀速率预测方法，即KPCA-CSO-RVM组合模型，并验证了该方法的预测精度。该方法先使用KPCA算法对工艺管道腐蚀速率的影响因素进行优选，然后使用CSO算法对RVM算法中的参数进行优选，再将现场获取的工艺管道腐蚀速率及其影响因素数据分为两组，分别为训练数据集和验证数据集，并使用训练数据集对组合模型进行训练，对验证数据集数据进行预测，计算预测误差，同时与其他模型的预测结果进行对比，以此证明该组合模型的可行性和先进性。

1 核主成分分析(KPCA)算法

通过对PCA方法进行改进后，即可得到核主成分分析(KPCA)算法，该算法主要是通过非线性的方式对其主成分进行合理的提取。在使用该算法的过程中，先对所有的样本数据

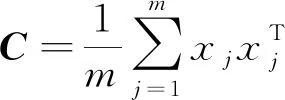
x

进行合理的非线性转变

φ

(

x

)，进而将所有的数据转换到高维空间

F

中，此时数据样本的协方差矩阵可以表示为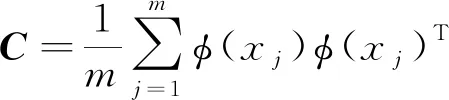

(1)

数据样本的协方差矩阵特征向量和特征值

λ

将会满足以下计算公式：

λ

-=0

(2)

此时引进非线性的函数

φ

(

x

)，就可以得到：

λφ

(

x

)-

φ

(

x

)=0

(3)

数据样本的协方差矩阵的特征向量可以使用非线性函数

φ

(

x

)进行表示，进而可以得到：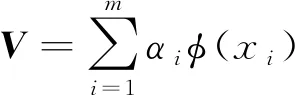

(4)

在此引入核函数

K

=

K

(

x

,

x

)=

φ

(

x

)

φ

(

x

)，并将公式(2)和(4)都代入到公式(3)中，简化后可以得到：

mλ

-=0

(5)

式中：表示核函数矩阵的特征向量。对于任意的数据样本而言，在高维空间

F

中非线性函数

φ

(

x

)的投影可以表示为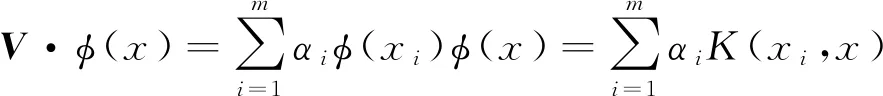

(6)

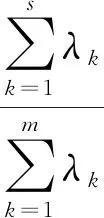
(7)

式中：表示

m

×

m

阶的矩阵，其系数为1

/m

。

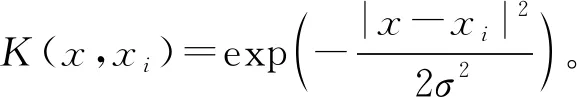
2 鸡群优化相关向量机算法

2.1 相关向量机(RVM)算法的基本原理

相关向量机(Relevance Vector Machine,RVM)算法是一种基于贝叶斯理论的机器学习方法，由国外学者Tipping在2000年提出，该算法主要是通过对先验数据进行一定的筛选，进而删除不相干的点，保留可以体现数据特征的相关向量，最终得到稀疏化的数学模型。RVM算法与支持向量机(SVM)算法具有一定的相似之处，但是该算法在对核函数进行选择的过程中，并不需要遵从Mercer定理的约束，进而使得核函数的计算量大幅下降，计算过程将更加的高效。

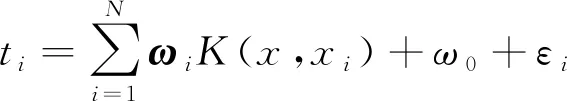
(8)

式中：表示数学模型的权重向量，=(

ω

,

ω

,…,

ω

)；

K

(

x

,

x

)表示模型的核函数；

ω

表示偏差；

ε

表示遵循高斯分布(0,

σ

)的噪声，该噪声满足

ε

～

N

(0,

σ

)。由于

t

属于一个独立的分布样本，所以该样本的似然估计可表示为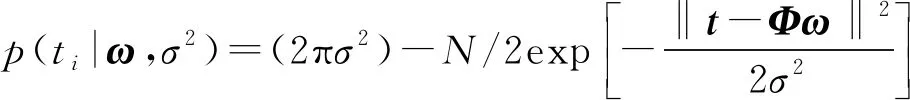

(9)

式中：表示权重向量矩阵;表示样本矩阵;表示核函数的矩阵，=[

φ

,

φ

,…,

φ

]，其中

φ

表示基函数，

φ

=[1,

K

(

x

,

x

),…,

K

(

x

,

x

)]。为了防止在使用RVM模型的过程中出现过学习的问题，所以该模型中的权重向量将会满足高斯先验概率的基本分布：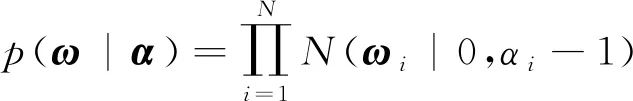

(10)

式中：表示超参数向量，=[

α

,

α

,…,

α

]，该向量与权重向量之间呈现出相互对应的关系，同时也将直接决定权重向量的先验分布情况。通过使用Bayesian理论，权重向量的后验分布可表示为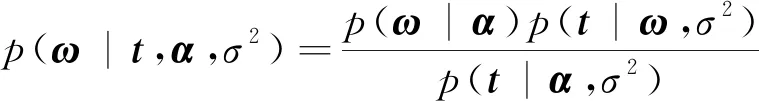

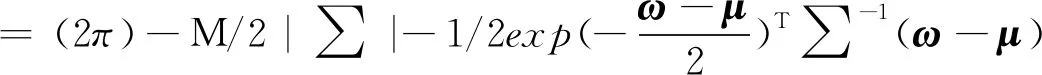
(11)

式中：表示均值向量，=

σ

∑；∑表示协方差矩阵，∑=(

σ

+)-1，其中表示对角矩阵，=diag(

α

,

α

,…,

α

),

M

=

N

+1。在对公式(11)中的进行积分后，就可以得到由、

σ

两项参数所决定的边缘分布：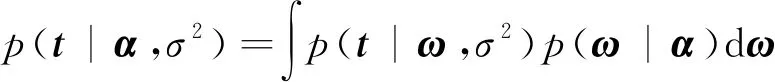

(12)

此时、

σ

两项参数的边缘似然估计可表示为

p

(|,

σ

)=

N

(0,

R

)

(13)

式中：

R

=

σ

+，其中表示单位矩阵。由于无法得到公式(13)的解析解，所以需要对其进行迭代计算，在计算过程中，参数

σ

、的最优解可表示为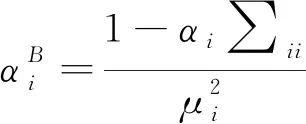

(14)

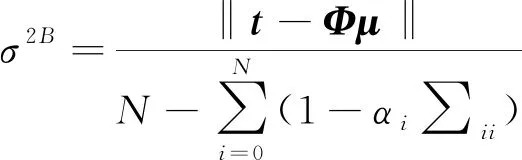
(15)

式中：∑表示协方差矩阵∑之中第

i

个对角所对应的元素。在已经给定训练样本数据的前提下，首先对参数、

σ

的初值进行假定，通过使用公式(14)和(15)对其进行迭代，直到相关参数都已经收敛为止，此时RVM模型就已经训练完成。在使用RVM模型算法的过程中，核函数的选择将会对模型的训练及预测效果产生重要的影响，因此本次研究中将会选用高斯径向基核函数作为RVM模型的核函数，该核函数具有很强的非线性处理能力。高斯径向基核函数

K

(

x

,

x

)可表示为

K

(

x

,

x

)=exp[-‖

x

-

x

‖

/

(2

γ

)]

(16)

式中：

γ

表示核函数的宽度。

2.2 鸡群优化(CSO)算法的基本原理

鸡群优化(Chicken Swarm Optimization,CSO)算法是一种根据鸡群的觅食行为以及鸡群内的等级观念所建立的一种优化算法，该算法于2014年由国外学者Meng等所提出。该种优化算法建立在理想化的基础上，可以将其简单描述为：根据鸡群中公鸡的个数，将整个鸡群分为多个子群，每个子群中公鸡都将占主导地位，每个子群中也只有1只公鸡，同时子群中还含有大量的母鸡以及雏鸡，公鸡、母鸡、雏鸡的数量是根据整个鸡群的适应度所决定的，此时公鸡的个数将直接决定鸡群中子群的数量，而母鸡和雏鸡将会被随机地分配到每一个子群之中，雏鸡将会由母鸡所领导，进而开展搜索行为，母鸡将会受到公鸡的领导，在建立起这种关系以后，该种等级观念将会持续到第

G

代，在第

G

代之后就会进行更新，更新就是根据鸡群的适应度对子群进行重新的划分。首先假设鸡群的搜索空间维数为

D

，鸡群中共有

N

个个体，其中公鸡的数量为

N

，母鸡的数量为

N

，雏鸡的数量为

N

，雏鸡与母鸡之间存在母子关系的母鸡数量为

N

，

N

将会在

N

个母鸡之中随机地进行选择。由于在所有子群之中公鸡的适应度相对较好，所以对公鸡位置进行更新的模型可以用以下公式表示：

x

,(

t

+1)=

x

,(

t

)[1+randn(0,

σ

)]

(17)

其中：

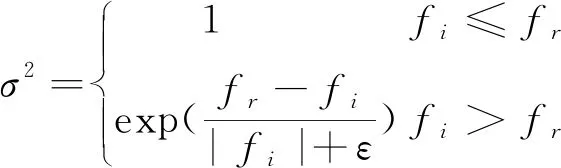
(18)

上式中：

x

,(

t

+1)表示第

t

+1次迭代过程中第

i

只公鸡在第

j

维空间中的位置；

x

,(

t

)表示第

t

次迭代过程中第

i

只公鸡在第

j

维空间中的位置；randn(0,

σ

)的平均值为0，其标准差

σ

将会服从高斯分布；

ε

表示一个相对较小的常量；

f

表示第

i

只公鸡所对应的适应度；

f

表示第

r

只公鸡所对应的适应度；

r

∈[1,

N

],但

r

≠

i

。

在子群之中，母鸡的适应度低于公鸡，所以母鸡的觅食将会受到公鸡的严重影响，同时也会对其他鸡发现的食物进行偷取，在进行食物竞争的过程中，适应度高的母鸡更具有优势。母鸡所对应的位置可以用以下公式进行更新：

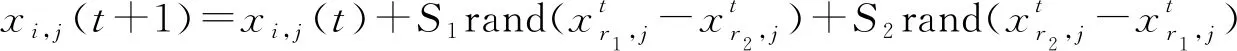
(19)

其中：

S

=exp[(

f

-

f

)

/

(|

f

|+

ε

)]

(20)

S

=exp(

f

2-

f

)

(21)

上式中：rand表示区间[0,1]之内的任意数；

r

表示第

i

只母鸡所对应子群之中的公鸡；

r

表示除了雏鸡以外子群中的任意个体，

r

≠

r

；

f

表示

r

的适应度；

f

表示

r

的适应度。

由于雏鸡的适应度最低，因此雏鸡只能跟随与自身具有母子关系的母鸡进行觅食，觅食的范围相对较小，雏鸡的位置可以用以下公式表示：

x

,(

t

+1)=

x

,(

t

)+

FL

[

x

,(

t

)-

x

,(

t

)]

(22)

式中：

m

表示第

i

只雏鸡所跟随的母鸡；

x

,(

t

)表示雏鸡跟随母鸡所在的位置；

FL

表示跟随系数，其可以在区间[0,2]之内进行取值。

2.3 CSO-RVM组合模型的构建

在使用RVM算法模型的过程中，核函数参数的选择会对RVM模型的学习及预测效果产生严重的影响，目前并没有统一的确定核函数参数的方法，由于CSO算法在使用的过程中需要人为设定的参数相对较少，且算法较为简单、收敛速度也相对较快，所以在本次研究中将使用CSO算法确定RVM算法中的核函数宽度

γ

。CSO-RVM组合模型的构建流程如图1所示。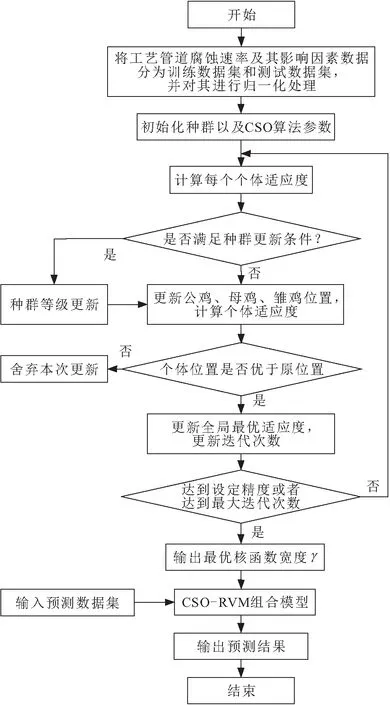

图1 CSO-RVM组合模型的构建流程

3 实例验证

3.1 模型组合的必要性分析

使用KPCA-CSO-RVM组合模型对工艺管道腐蚀速率进行预测研究的过程中，KPCA算法可以对工艺管道腐蚀速率的影响因素进行优化，从而优选出对工艺管道腐蚀速率产生影响的主要因素，这将有利于简化工艺管道腐蚀速率预测模型，降低模型预测的难度。在使用RVM算法对工艺管道腐蚀速率及其影响因素数据进行学习及预测的过程中，部分参数需要设定，如果人为地进行参数设定会使得模型的预测精度降低，因此本次研究通过引入了CSO算法，对RVM算法中的相关参数进行优化，确定最佳的参数，并将参数输入到RVM算法中，以提高工艺管道腐蚀速率预测的精度。

3.2 数据来源

在本次研究中，所使用的工艺管道腐蚀速率及其影响因素数据来自于我国东北地区某石油化工企业内的3条原油工艺管道，该3条原油工艺管道在不同条件下的腐蚀速率及其影响因素数据，见表1。其中，工艺管道腐蚀速率数据通过电阻探针获取；部分影响因素数据通过采样的方式获取；管道运行压力和运行温度数据通过现场的监测仪表获取。对于该石油化工企业而言，影响工艺管道腐蚀速率的因素主要可以分为8项，分别是管道的运行压力、运行温度，原油中的硫含量、CO含量、氮含量、氧含量，原油的流速和pH值。本次研究将每条工艺管道看作为一个数据集，共有3个数据集，每个数据集中含有24组数据。为了验证本文所提出的基于KPCA-CSO-RVM组合模型的工艺管道腐蚀速率预测方法的预测效果，在每个数据集中选择20组数据对模型进行训练，对数据集中剩余4组数据进行预测，并对3个数据集预测结果的平均相对误差进行了计算，以检验该组合模型的可行性和先进性。

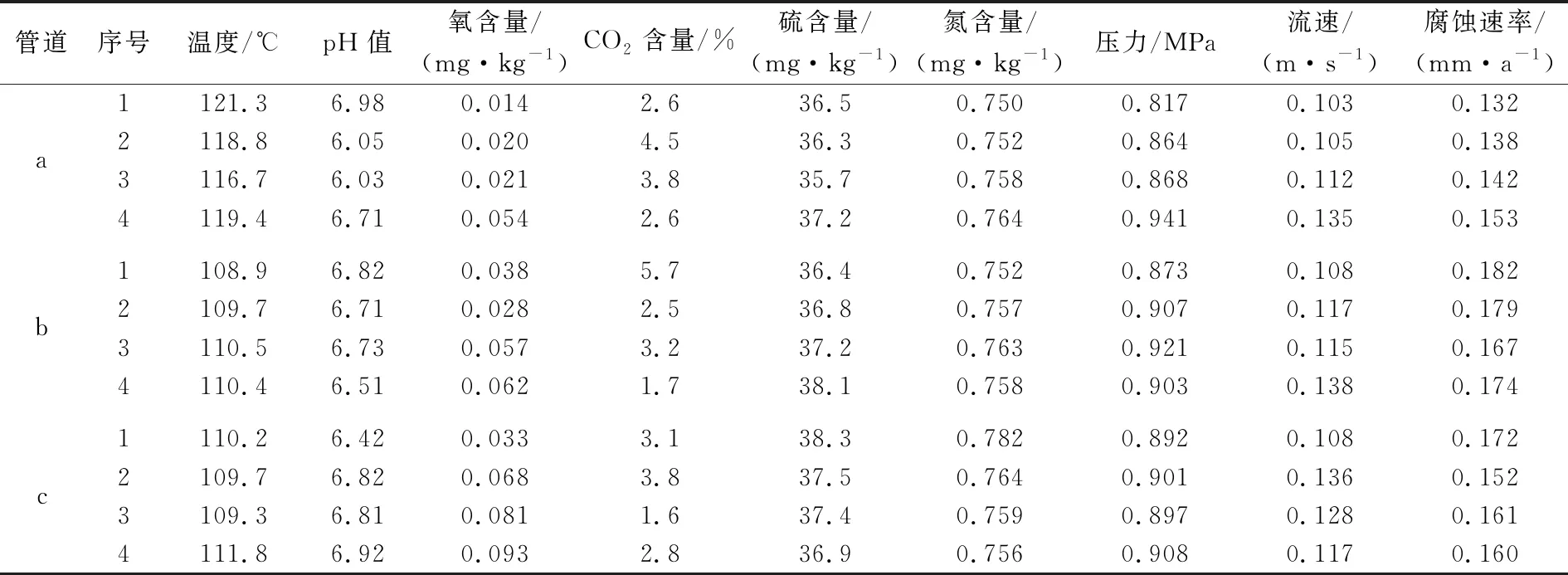
表1 3条工艺管道的部分腐蚀速率及其影响因素数据

3.3 KPCA结果分析

使用上述介绍的KPCA算法对工艺管道腐蚀速率及其影响因素数据进行训练处理，进而可以得到对工艺管道腐蚀速率影响相对较大的因素，并根据每个影响因素的贡献率，计算累计贡献率，其计算结果见表2。

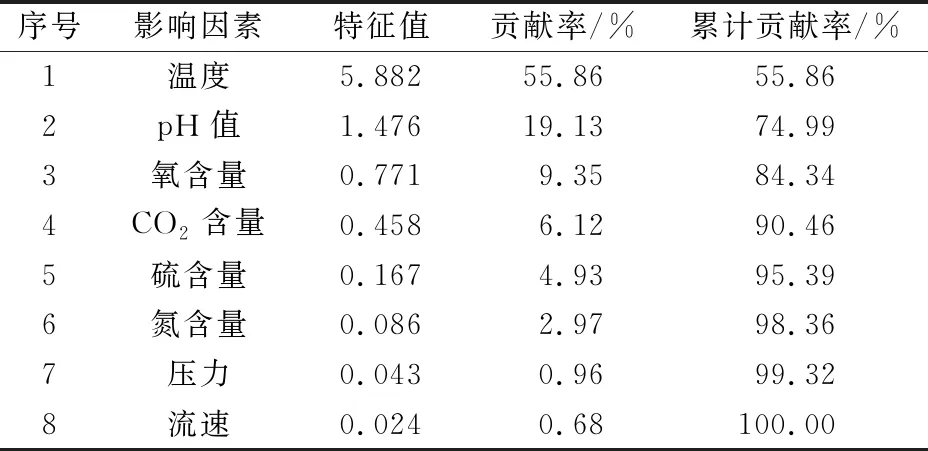
表2 工艺管道腐蚀速率不同影响因素的特征值和累计贡献率

通过对表2中数据进行分析可以发现，前4个影响因素的累计贡献率已经超过了85%，因此在接下来的研究中可以使用前4个影响因素作为CSO-RVM模型的输入，进而建立CSO-RVM组合模型。另外，通过对原始样本进行分析可以发现，在使用KPCA算法的过程中，可以最大程度地保留原始样本的基本信息，进而实现影响因素的降维处理，即将原来的8个影响因素减少为4个，使得影响因素之间的冗余性得到了降低，这为建立CSO-RVM组合模型进行下一步的研究奠定了基础。

3.4 CSO-RVM组合模型预测效果的验证

在使用CSO-RVM组合模型对工艺管道腐蚀速率进行预测的过程中，为了提高该组合模型的预测效果，首先使用CSO算法对RVM算法中的高斯径向基核函数宽度

γ

进行优选，其取值范围为[0.01,1]。在使用CSO算法的过程中，将该算法的迭代次数设定为100次，共进行10代更新，鸡群中公鸡、母鸡以及雏鸡的个数分别设定为10只、20只、20只，其中与雏鸡之间存在母子关系的母鸡数量为5只。使用CSO算法对核函数宽度

γ

进行优选的过程中，其迭代曲线见图2。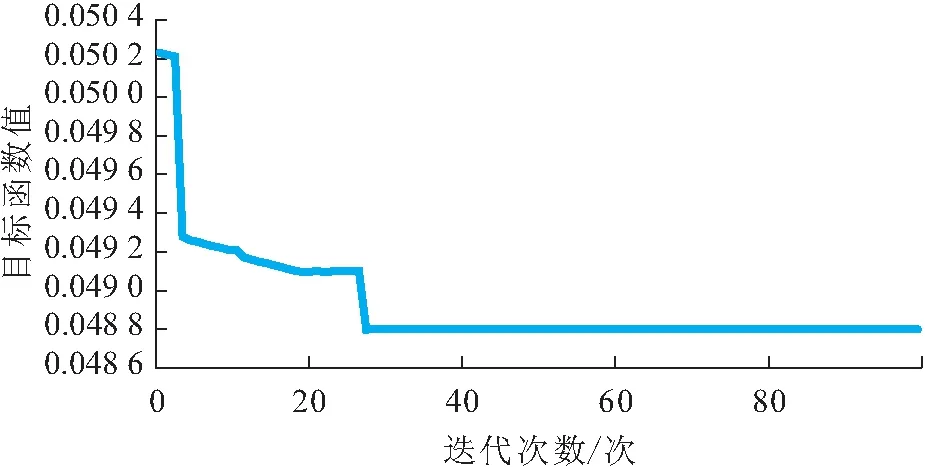

图2 鸡群优化(CSO)算法迭代曲线

通过对图2进行分析可以发现，当CSO算法迭代到27次时，迭代曲线已经收敛，所以优选的核函数宽度

γ

为0.639 4，在对核函数宽度进行优选以后，即可建立RVM模型。

为了对本研究所提出的预测方法进行验证，将该3条工艺管道的腐蚀速率及其影响因素数据看作3个数据集，利用每个数据集中的20组数据对模型进行训练，对数据集中剩余的4组工艺管道腐蚀速率数据进行预测，使用CSO-RVM组合模型对3条工艺管道腐蚀速率进行预测的结果见图3至图5。

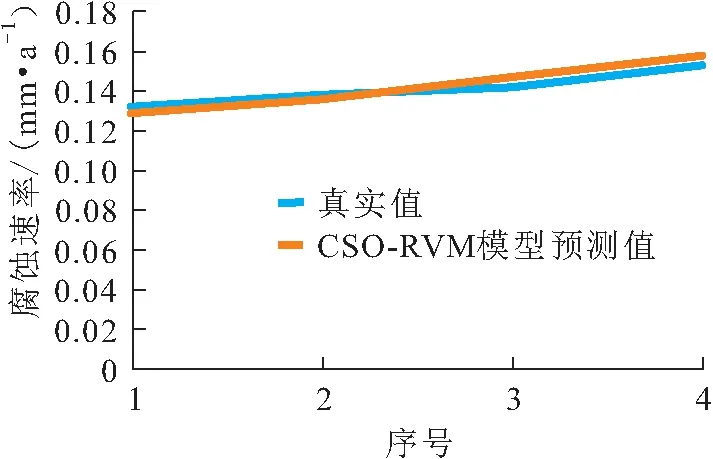
图3 工艺管道a的4组腐蚀速率CSO-RVM组合模型预测值与真实值对比

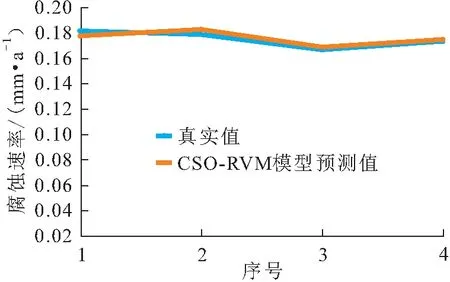
图4 工艺管道b的4组腐蚀速率CSO-RVM组合模型预测值与真实值对比

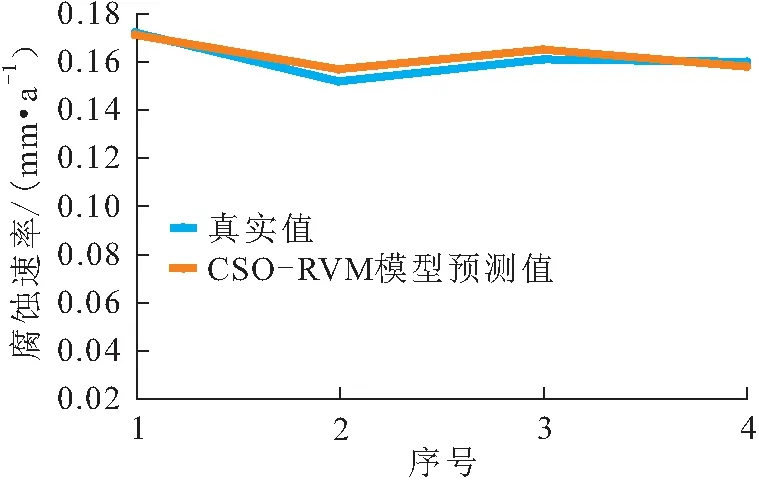
图5 工艺管道c的4组腐蚀速率CSO-RVM组合模型预测值与真实值对比

由图3至图5可见，工艺管道a、b、c腐蚀速率的预测值与真实值基本一致，每组验证数据集的预测结果都可以很好地逼近工艺管道腐蚀速率的真实值，证明本文所提出的基于KPCA-CSO-RVM组合模型的工艺管道腐蚀速率预测方法具有可行性。

为了进一步证明本文所提出的预测方法的先进性，使用每个数据集中的20组数据对KPCA-CSO-RVM组合模型、RVM模型、常见的SVM(支持向量机)模型和BP神经网络模型进行训练，对每个数据集中剩余的4组工艺管道腐蚀速率数据进行预测，统计每种预测模型预测结果的最大相对误差，并计算所有预测模型预测结果的平均相对误差、均方根误差，得到不同预测模型的误差对比,见表3。

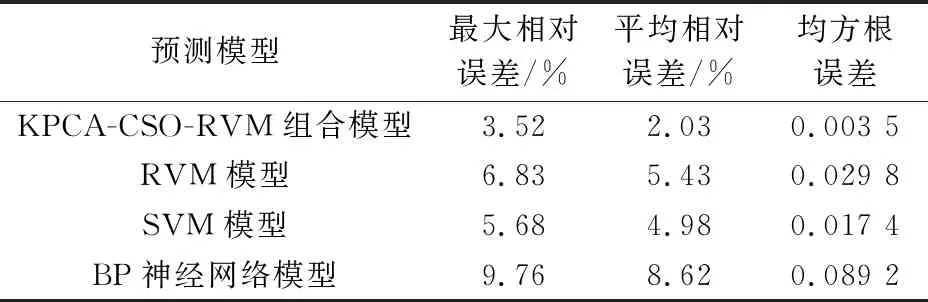
表3 不同预测模型的误差对比

通过对表3中数据进行分析可以发现，本文所提出的KPCA-CSO-RVM组合模型在对工艺管道腐蚀速率进行预测的过程中，其预测结果的最大相对误差、平均相对误差、均方根误差均小于其他3种预测模型，证明本文提出的KPCA-CSO-RVM组合模型具有先进性。

4 结 论

针对工艺管道腐蚀速率预测问题，本文提出了一种基于KPCA-CSO-RVM组合模型的工艺管道腐蚀速率预测方法，该方法首先对KPCA算法、CSO算法和RVM算法进行了理论介绍，提出了3种算法的组合方法;然后使用我国某石油化工企业内3条原油管道腐蚀速率及其影响因素的一部分数据对该组合模型进行了训练，对另一部分数据进行了预测验证，得到以下结论：

(1) 通过使用KPCA算法对工艺管道腐蚀速率的影响因素进行分析可以发现，温度、pH值、氧含量和CO含量是影响工艺管道腐蚀的4大重要因素，这4个影响因素对工艺管道腐蚀速率的累计贡献率超过了85%，并使用KPCA算法对工艺管道腐蚀速率影响因素进行降维处理，将原来的8个影响因素减少为4个，使得影响因素之间的冗余性得到了降低。

(2) 使用KPCA-CSO-RVM组合模型对工艺管道腐蚀速率进行预测的过程中，工艺管道a、b、c腐蚀速率的预测值与真实值基本一致，每组验证数据集的预测结果都可以很好地逼近工艺管道腐蚀速率的真实值，证明本文所提出的基于KPCA-CSO-RVM组合模型的工艺管道腐蚀速率预测方法具有可行性。

(3) 将本文所提出的基于KPCA-CSO-RVM组合模型的工艺管道腐蚀速率的预测结果与其他常见模型的预测结果进行对比后发现，本文所提出的KPCA-CSO-RVM组合模型对工艺管道腐蚀速率预测结果的最大相对误差、平均相对误差、均方根误差均小于其他3种预测模型，证明本文所提出的组合模型具有先进性。