基于三维空间的地理要素表达新形式

邹娟茹，孙兴华，唐红涛，李 昂

（1.杨凌职业技术学院,陕西 杨凌 712100；2.陕西省交通规划设计研究院有限公司,陕西 西安 710065；3.中国地震局第二监测中心,陕西 西安 710054；4.西安科技大学,陕西 西安710054）

为了避免投影变形给工程建设带来的不利影响,传统纸质或DLG均采用国家标准分幅地形图,特别是在大区域的地图制图等相关领域。传统做法纵然解决了投影变形问题,但给实际设计、勘察工作带来了一定的不便[1-3],如大量纸质分幅地形图将导致图纸打印、存放与保管等诸多问题,较大区域的工程项目需经常根据当地中央子午线进行转换（如东西走向省道或国道的测设与测定,每隔若干km需进行一系列的坐标换带工作,且在控制测量中的相邻两带接边处5 km内的控制点均需给出东西两带的两套坐标）等。随着计算机技术的迅猛发展,电子地图工程设计、数值建模已逐渐替代了传统纸质地图,因此在长距离、大区域的工程设计和地理信息要素表达中,传统分幅地形图已逐渐淡出视野,而基于参考椭球面的地理要素表达形式孕育而生。

国内外在现代GIS三维地理信息的表达方面也日趋成熟,但其应用目的主要还是对三维地理信息属性和可视化的展示与管理,且展示区域较小；同时三维模型对计算机硬件要求非常高,并不完全适用于具有精确量测与大区域测绘方案的大型施工项目。本文利用大地测量学中大地线的理论特性,基于VC++平台,编写了基于参考椭球面两点大地坐标进行等间距内插空间直角坐标的解算程序；并通过实例,在三维模拟空间构建了参考椭球,绘制了大地线,再将其转换至GIS平台下,实现了图形与属性的挂接、编辑和查询。

1 大地线的内插

工程测量中小区域可采用独立坐标系,成图时即可使用自由分幅地形图；而小比例尺大区域地图制图或GIS工程中则最好采用三维电子数字地图,地理要素的三维空间表达正好能满足这两种需求。大地线是三维数字地图中最基本的表达要素,线、面、体均可由大地线来组合表达,而且大地线在教学与科学研究上具有重要的理论物理意义,但在实践绘制与表达上,缺少其搭载平台与表达形式,因此大地线的解算与绘制是关键的技术环节。

本文利用大地线等间距内插的原理,将三维空间大地线进行等距离内插,解算得到每个内插点的大地坐标,再利用三维多段线依次连接各内插点,形成三维空间大地线。具体算法流程（图1）为:①根据大地坐标D1(B1,L1)、D2(B2,L2)进行大地坐标反算,得到两点间的大地线长S、正方位角A12与反方位角A21；②利用克莱劳恒等式rBsinA=C和D1点的大地坐标方位角A12计算大地线常数C；③由D1点坐标D1(B1,L1)、A12、ds进行Bessel大地主题正算,得到第一个内插点的大地坐标(L1,B1)；④由大地线常数C和第一个内插点坐标(L1,B1)求取该点前进方向的大地方位角A1；⑤根据点P1(B1,L1)和克莱劳定理解算大地线常数C和第一个内插点前进方向的大地方位角A1,并可推算出第二个内插点的大地坐标(L2,B2)和该点的前进方向的大地方位角A2,以此循环推算得到大地线各内插点的大地坐标[4-10]。

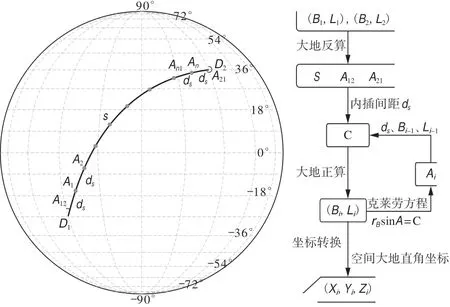
图1 大地线内插算法流程图

2 算例分析

在三维模拟空间,利用各内插点位的大地坐标(Li,Bi)进行大区域地理要素的绘制与表达是很难实现的,因此需要将求解得到的所有内插点大地坐标转换为其对应参考椭球下的空间大地直角坐标(Xi,Yi,Zi)。基于空间大地直角坐标,在三维空间模型中利用三维多段线的属性可将内插的三维多段线绘制于参考椭球面上（图2）,解算结果如表1所示。由图2可知,若绘制P1、P2两点间的大地线,则需根据图1的解算流程进行大地线等间距内插,P1、P2的两端点均位于北半球,在WGS84椭球下的大地坐标分别为P1（24°32′36.547901″,30°29′56.328726″）、P2（66°54′32.667469″,106°48′22.366306″）,内插点的密度由等间距ds来控制,本文设置的内插间距ds为10 km,即每隔10 km内插一个点。利用编制的大地线内插求解程序,可解算得到P1至P2的方位角A12为25°34′56.079039″,P2至P1的反方位角A21为267°47′55.802300″,两点间大地线长S为6 923 514.359 747 m,内插点共计692个,最终得到的内插点是大地坐标,还需将其转换为同一椭球下的空间大地直角坐标。解算采用1975国际椭球参数,第一个内插点处大地方位角为25°35′59.949871″,最后一个内插点的大地方位角为87°43′29.091042″,即在P1至P2的内插与绘制过程中,其大地方位角是不断变化的,随着纬度的增加而递增。此外,由克莱劳恒等式rBsinA=C可知,C为常数,如图2所示,低纬度平行圈A1的半径R1较大,纬度增大至P2附近,平行圈A2的半径R2较小,随着纬度的增加平行圈半径逐渐减小,因此内插点大地方位角是递增的（小于90°）。

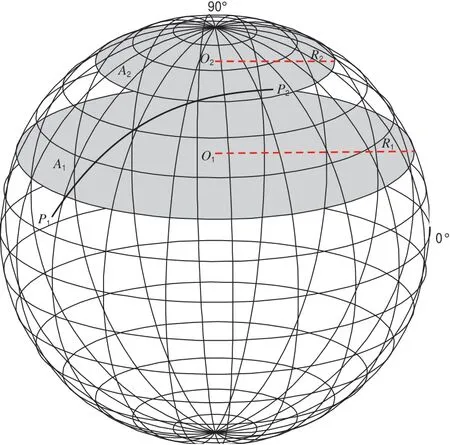
图2 参考椭球面大地线的表达形式

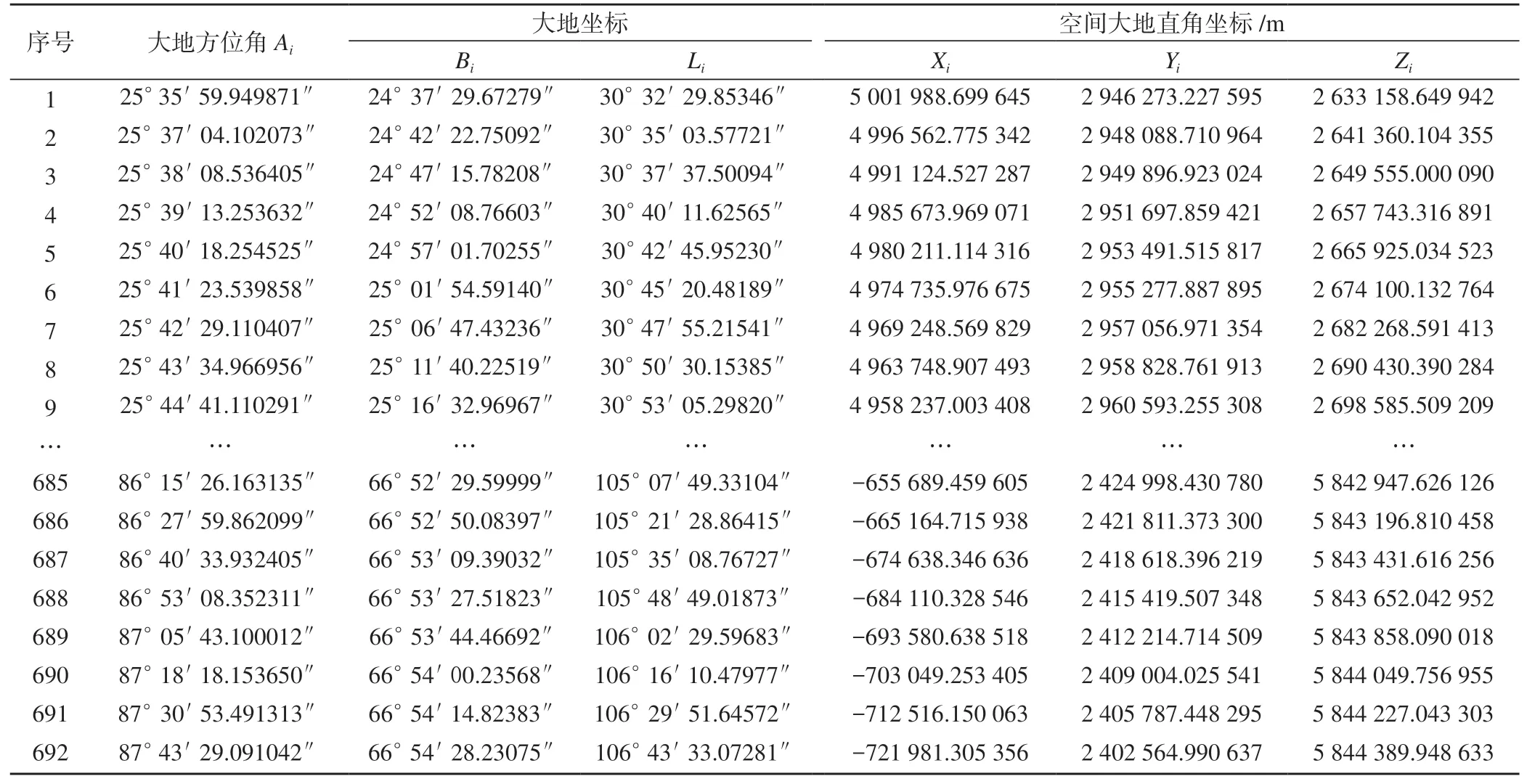
表1 算例计算与转换结果

3 内插精度的探讨

本文对三维大地线内插的精度做了相关探讨,如表2所示,根据理论值,对内插间隔做了3次调整,分别为20 km、10 km和5 km。与理论值相比,大地线长度内插精度分别为-18.326 523 cm、-9.365 442 cm和-3.832 412 cm,因此应用于工程领域时,并非内插点越密越好,只要达到工程精度要求即可。

表2 大地线内插精度表

4 三维数字地图实例

基于大地线的表达原理和算法基础,即可实现长距离、大区域地理要素在三维空间的具体表达。本文在三维模拟空间建立了参考椭球面,如图3a所示,利用内插点最终的空间大地直角坐标绘制了青海省与甘肃省的省界,该DLG的线状与面状要素均为三维地理要素；为了更加直观,将其进行放大、旋转（图3b）,可以看出,大区域的DLG是紧密贴附在参考椭球面上的,且该三维空间模型具备实时缩放、空间精密量测、多角度旋转与编辑等功能。

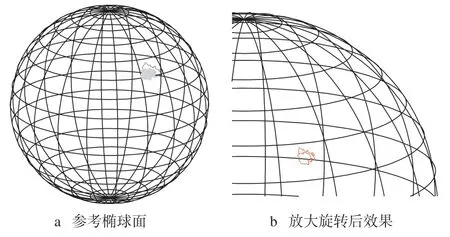
图3 三维空间模型中DLG的表达

5 结 语

本文基于大地测量学中大地线的理论特性,运用VC++软件,编制了基于参考椭球面两点大地坐标进行等间距内插空间直角坐标的解算程序。通过实例,在三维模拟空间构建了参考椭球,绘制了大地线,并将其转换至GIS平台,实现了图形与属性的挂接、编辑与查询[10]。

与传统DLG地形图的绘制、成图标准以及目前三维模拟地球（如Google Earth,无法精密量测,不能满足工程需求）相比,三维空间地理要素的表达形式更贴近现实和逼真,这种表达效果不仅解决了传统地图的投影变形问题,而且实现了地理要素图形与属性的编辑、查询、精密量测功能,能为今后三维数字地图的发展以及在地图制图、大区域测绘、地理信息工程等相关领域的应用提供一定的参考。