基于MCKD和VMD关联维数的轴承故障特征提取AR模型*

申 童，刘复秋宣，高学亮，岳晓峰

（长春工业大学机电工程学院，长春 130012）

0 引言

滚动轴承广泛应用于旋转机械设备中，其运行状态直接影响设备的性能和安全。据统计，引起旋转机械故障的原因中，滚动轴承所占比重在70%以上[1]。受限于工作环境，振动测试传感器采集到的冲击成分往往比较微弱，导致滚动轴承早期故障特征淹没在噪声中，难以被准确提取和识别。因此，滚动轴承早期故障诊断一直是研究的重点和难点[2－4]。

针对上述问题，常用的时频分析方法有经验模态分解（Empirical Mode Decomposition，EMD）、总体平均经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）、局部经验模态分解（Local Mode Decomposi⁃tion，LMD）等。徐卓飞等[5]把EMD和主成分分析相结合，利用统计学特性，分析了振动信号时域特征和故障模式之间关系；董文智等[6]提出了EEMD能量熵和支持向量机相结合的方法，通过计算能量熵值判断是否发生故障，并把特征向量输入到支持向量机中，有效地进行了轴承故障分类；张淑清等[7]提出了LMD近似熵和模糊C结合的方法，通过近似熵值做特征提取向量，并用FCM模糊聚类对故障进行准确识别分类。虽然这些方法能为轴承故障诊断特征提取提供一定的参考，但EMD存在着端点效应、算法效率低的问题，EEMD虽有所改善，仍摆脱不了计算效率差、模态混叠的状况，LMD存在着统计偏移和最佳结构元素选择问题[8]。这些问题都影响了对轴承故障特征准确度的辨识。2014年Dragomiretskiy等[9]提出一种自适应的信号处理方法——变分模态分解（Variational Mode Decomposition，VMD），该方法将信号分量的获取过程转移到变分框架内，采用一种非递归的处理策略，通过构造并求解约束变分问题实现对原始信号的分解，具有坚实的数学理论基础。最大相关峭度解卷积（Maximum Correlated Kurtosis Deconvolution，MCKD）是McDonald等[10]在2012年以最小熵解卷积为背景，提出的一种具有良好去噪能力、凸显故障特征的新方法。该方法通过相关峭度评价指标，不断迭代实现解卷积，从而凸显被噪声淹没的连续脉冲序列[11]。

基于上述分析，针对滚动轴承早期微弱故障难以提取的问题，为增强轴承振动信号中的冲击成分，降低噪声影响，本文提出一种基于MCKD和VMD关联维数的滚动轴承故障诊断AR模型，首先利用MCKD对故障信号进行降噪，再通过VMD对降噪后的信号进行分解，重构信号建立AR模型，获取自回归参数，最后通过计算自回归参数的关联维数对滚动轴承故障进行诊断。

1 MCKD算法

MCKD算法通过计算寻找一适用的长度为l的滤波器f(l)，使分析信号中冲击成分的相关峭度值最大，从而恢复其自身特性，滤除信号x内噪声干扰成分，相关峭度可定义为：

为获取能够使MCKM(T)最大的一个最优滤波器，令：

式中：T为信号中冲击成分的周期；M为位移数；f为滤波器内向，f＝[f1.f2.….fL]T。

对上述问题进行优化求解并转化为矩阵形式，最终滤波器系数可表示为：

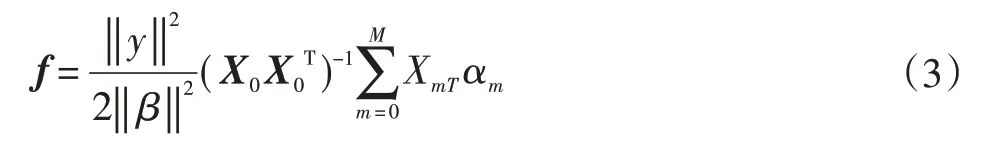
将上式所得滤波器系数组合f代入公式（2），即可获得采集信号x中的故障冲击成分y。

2 VMD算法

VMD方法根据模态分解个数K将原始信号f（x）分解为K个中心频率为ωk(t)的模态函数uk(t)，该方法将IMF分量重新定义为一具有限带宽的调幅－调频信号。

式中：Ak(t)≥0为uk(t)的瞬时幅值；ωk(t)为uk(t)的瞬时频率；φk(t)为非递减相位函数。为估算出每个IMF分量的带宽，首先对每个模态函数uk(t)进行Hilbert变换，得到边际谱；然后向各模态解析信号内添加指数项，将uk(t)频谱变换至基带上；最后计算解析信号梯度的平方L2范数，从而获得模态函数的带宽。

则受约束变分问题模型为：

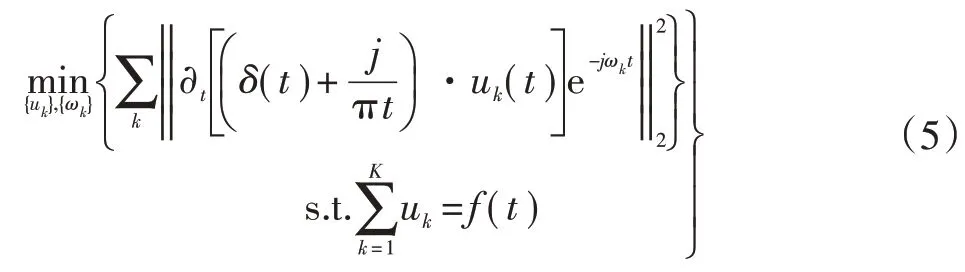
式中：{uk}={u1.u2.….uk}，为VMD分解所得各IMF分量；{ωk}={ω1.ω2.⋅⋅⋅.ωk}，为各IMF分量的中心频率；δ(t)为脉冲函数。

引入二次惩罚因子和拉格朗日乘法算子求解上述约束变分问题的最优解，通过乘法算子交替方向法交替更新和λn+1以获取扩展拉格朗日表达式的鞍点。求模态函数取值问题则可表达为：

则求得的模态分量uk及中心频率ωk分别为：

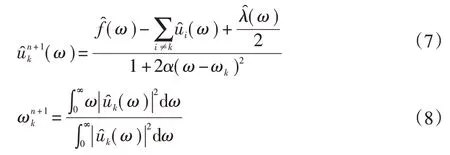
对于给定判定精度e>0，当满足式（8）时分解迭代停止，并由此得到最终模态分量及对应中心频率ωk。

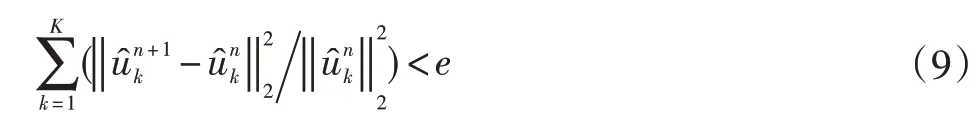
3 VMD关联维数的AR模型

设信号经VMD分解所得K个IMF分量，其中对故障特征敏感的IMF分量为p个，将p个IMF分量形成重构信号z(t)，对其建立AR模型AR(m)：

式中：φk(k=1.2.···.m)、m分别为重构信号z(t)的AR(m)模型参数和阶数；e(t)为模型残差，关联维数计算时，采用G－P算法[12]。

设距离阈值为r，C(r)为距离rij小于r的点对数在所有点对数中的比例：

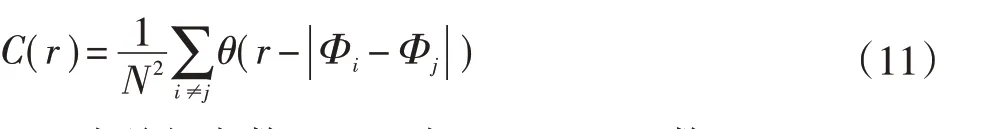
式中：N为总相点数；θ(x)为Heaviside函数。

C(r)为关联积分，是空间中两点间距rij＜r概率，选择恰当r的范围，使C(r)随着r的变化为：

式中：D为关联维数，可由下式求得：

分别以lnr和lnC(r)为横、纵坐标，则lnC(r)－lnr变化曲线的斜率对于逐渐增大的嵌入维数n逐渐收敛于一个值，则该值就是关联维数D。

4 试验研究

为了验证所提出的方法，本文采用的是美国凯斯西储大学的轴承信号集数据。其振动采集实验平台驱动端电机负载为1 HP，电动机转速为1 772 r/min，采样频率为12 kHz，采取故障较为微弱的0.007 in的轴承内圈、外圈和滚动体故障信号进行分析与验证，信号分析时长选取1 s，轴承型号为6205－2RS。

图1所示为一随机内圈故障信号频谱，其振动信号频谱中存在较多高频干扰噪声，轴承故障特征频率难以辨别，且低频特征噪声影响更明显。

图1 内圈故障信号频谱

为提升信号的信噪比，增强故障特征差异，本文对上述滚动轴承振动信号进行MCKD降噪，降噪后内圈故障的振动信号如图2所示。不同状态下滚动轴承振动信号经MCKD降噪后，信号内的绝大多数噪声成分得到有效滤除，信号内的冲击成分得以增强。MCKD降噪后信号的频谱如图3所示。对比图2和图3可知，经MCKD去噪后，内圈故障振动信号频谱内低频区域冲击成分的谱线峰值明显增多。

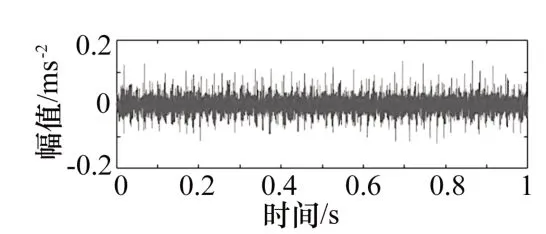
图2 MCKD降噪后内圈故障振动信号

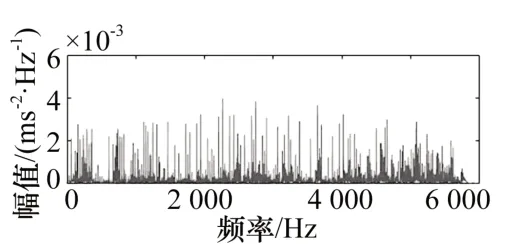
图3 MCKD降噪后内圈故障信号频谱

采用VMD方法对上述MCKD降噪信号进行分解，分解过程中，模态分解个数K＝6，惩罚因子α＝2 400，分解所得各IMF分量和其频谱如图4所示。由图可知，VMD分解结果中，各IMF分量间未出现明显的模态混叠问题，表明参数选取方法具有较好的适用性。

图4 MCKD降噪后内圈故障信号的VMD分解结果及各IMF分量频谱

为有效选取包含主要内圈故障特征信息的模态分量，进一步降低噪声成分的影响，分别计算各IMF分量的峭度和MCKD去噪后信号间的互信息熵，结果如表1所示。由表可知，IMF1和IMF3的峭度和互信息熵值较大，因此选取上述IMF分量对内圈故障信号进行重构，重构后信号的时域波形和频谱如图5~6所示。由图可知，内圈故障重构信号中的高、低频域内冲击成分谱线峰值得以明显增强。

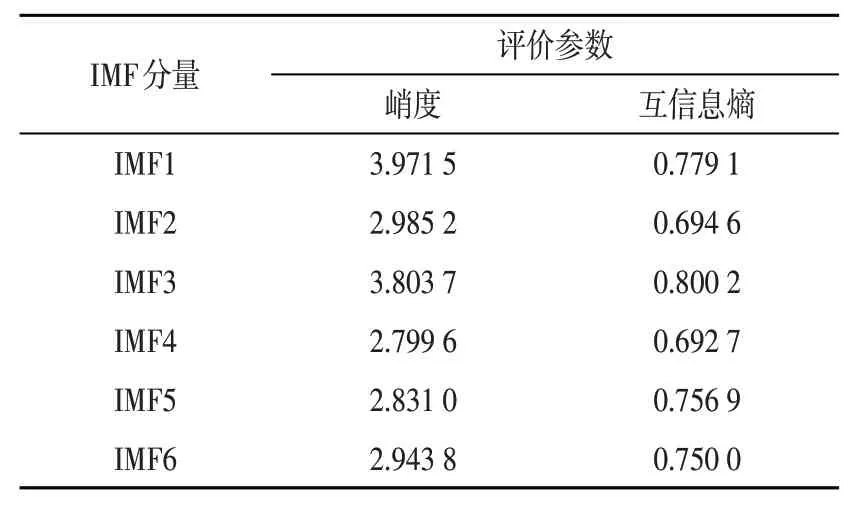
表1 内圈故障信号各IMF分量的峭度和互信息熵

图5 内圈故障重构信号的时域波形

按上述步骤分别对正常轴承、外圈故障轴承和滚动体故障轴承信号进行重构，所得重构信号时域波形和频谱如图7~8所示。对比图5和图7，图6和图8可知，重构信号中的冲击成分得到更加有效地突显，信号频谱中低频域内冲击成分的谱线峰值更加明显，为后续信号特征的准确提取提供了保证。

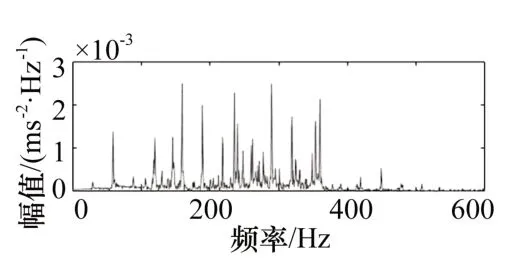
图6 内圈故障重构信号的频谱

图7 不同状态下滚动轴承重构信号时域波形

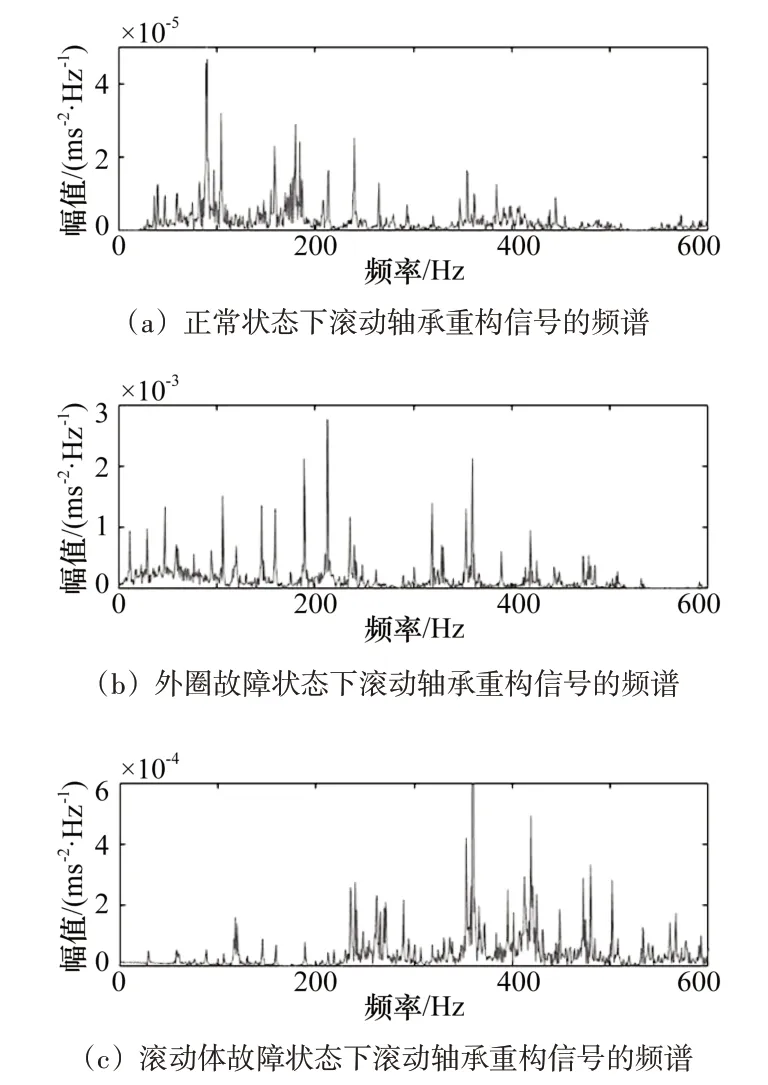
图8 不同状态下滚动轴承重构信号频谱

对图6和图8中不同状态下滚动轴承重构信号建立AR模型，采用最终预测误差准则确定模型阶数n，并通过时延相图法获取AR模型自回归参数的相空间。在此基础上，计算其关联维数，结果如图9所示。其中，嵌入维数取值范围为5～15。由此可知，不同状态下滚动轴承重构信号的关联维数除在个别嵌入维数上有所重叠外，具有较好的区分度。其中在嵌入维数为6～10区域内区分效果较为理想，说明可采用本文方法可实现对滚动轴承早期故障诊断。未经降噪处理的滚动轴承信号关联维数如图10所示，经MCKD去噪后的滚动轴承信号关联维数如图11所示。对比图9～11可知，不同状态下滚动轴承振动信号的关联维数较为接近，难以实现故障类型的有效区分和诊断。

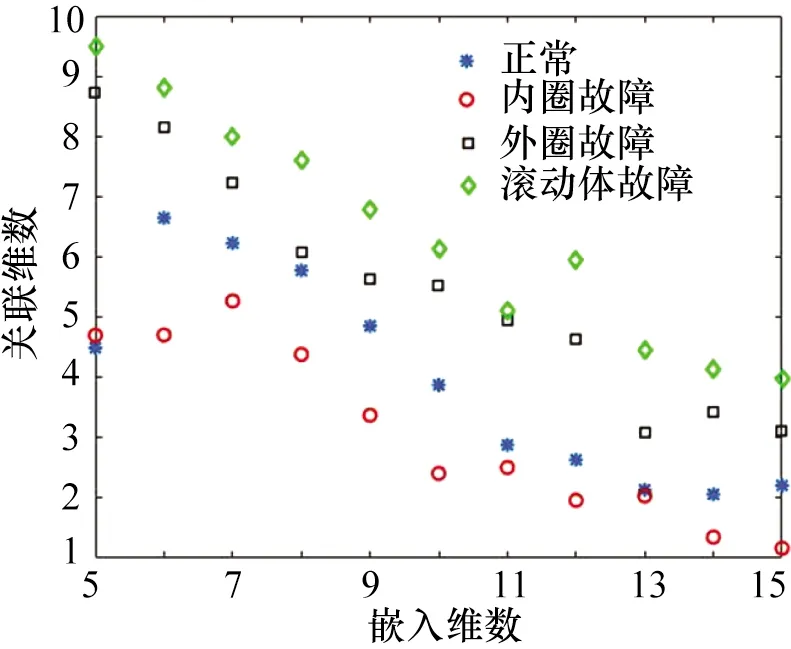
图9 不同状态重构信号AR模型自回归参数序列的关联维数

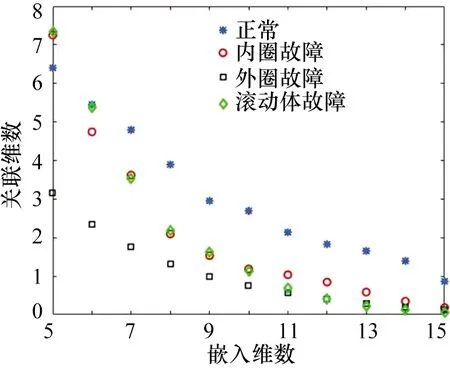
图10 不同状态下滚动轴承原始振动信号的关联维数

图11 不同状态下MCKD去噪后滚动轴承振动信号AR模型自回归参数的关联维数

采用所提方法对不同状态下滚动轴承的各10组振动信号进行MCKD降噪，并进行VMD重构，计算重构信号AR模型自回归参数序列的关联维数。

结合图10的分析，选择嵌入维数为6～10时关联维数的分布曲线对滚动轴承故障进行诊断，不同状态下各组信号的关联维数如图12所示。由图可知，在指定嵌入维数上，轴承外圈故障、内圈故障、滚动体故障经MCKD降噪和VMD重构的滚动轴承振动信号的关联维数具有良好的区分度，说明滚动轴承经MCKD去噪后，信号内的噪声干扰成分得到滤除，VMD重构实现了信号的非线性化，所建立AR模型的自回归参数序列包含了信号的自身特征信息，强化了特征差异，保证了关联维数计算的准确性，可以据此对滚动轴承的障类型进行诊断。

图12 不同状态下滚动轴承信号的关联维数

5 结束语

针对滚动轴承早期故障特征微弱，特征信息难以提取的问题，本文提出了一种基于MCKD和VMD关联维数的滚动轴承故障诊断AR模型。该模型采用MCKD对滚动轴承振动信号进行降噪处理，提升了信号的信噪比；根据峭度和互信息熵值对故障特征敏感的IMF分量进行信号重构，根据建立的AR模型，计算出在指定嵌入维数上自回归参数的关联维数。实验分析结果表明，所提出的AR模型在指定嵌入维数上可强化滚动轴承早期微弱故障特征差异，故障诊断结果准确有效。