基于DBN的配电网可靠性分析

孙园园，章文俊，单鸿涛，陈传涓，段传科

（1.上海工程技术大学 电子电气工程学院，上海 201620；2.中国电建集团装备研究院有限公司，上海 200233；3.国网安徽省电力公司蚌埠供电公司，蚌埠 233000）

0 引言

配电网是电力系统不可或缺的组成部分，其覆盖面广、对系统运行的可靠性影响大。针对配电网供电可靠性进行深入研究，以获取其更加快速、准确的分析方法具有重要意义[1]。

配电网供电可靠性分析方法主要包括模拟法、解析法及人工智能法等。其中常用的模拟法为蒙特卡洛（Monte Carlo）法，该法的计算精度与抽样次数相关，计算量大、每次计算所需时间长，难以满足在线分析的需求[2]；解析法一般包括状态枚举法[3]、故障模式影响分析法[4]及最小路法[5]等，其中，故障模式影响分析法较常用，但其分析难度随网络结构复杂度的增长而剧增，导致计算量大、计算速度慢；人工智能方法中神经网络算法最为常见，神经网络算法基于历史样本数据进行分析，其自适应能力强，训练好后可靠性分析时间及计算量有所减少，但计算精度有待提高[6]。

本文提出了基于深度信念网络的配电网可靠性分析模型，该模型既弥补了以往神经网络在可靠性分析中精度不高的缺陷，又解决了模拟法、解析法计算量大、耗时长、难以满足在线分析需求等问题。所用深度信念网络具有多个隐含层，从而可以包含更多配电网相关信息、获取样本数据的更深层本质特征。采用训练好的深度学习网络进行配电网可靠性分析，速度快且所得结果误差微小。本研究可为配电网的规划及运行提供合理依据，对配电网的成本效益分析也有较高的参考价值。

1 深度学习模型的设计

深度学习的模型主要包含深度信念网络（DBN）、卷积神经网络（CNN）及循环神经网络（RNN）等[7]。其中DBN模型较为灵活，它融合了无监督学习与有监督学习的优点，可从海量样本中学习、提取数据集的本质特点，因此本文采用由数个受限玻尔兹曼机（RBM）堆叠形成的DBN模型进行配电网可靠性分析。每个RBM各由一个可视层及一个隐含层构成，具有很强的无监督学习能力，可自动提取样本中的繁杂规则[7]。

DBN的训练分为预训练和反向微调两个过程，预训练时首先以可视层v1和隐含层h1构成RBM1，对之加以训练，而后将h1视为可视层v2，与隐含层h2构成RBM2，进行RBM2的训练学习，RBM2的隐含层又被视作RBM3的可视层，以此类推，直至所有RBM训练结束[8]。DBN结构模型示意图如图1所示。

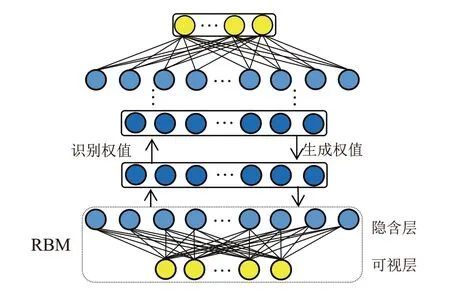
图1 DBN结构模型示意图

受限玻尔兹曼机同层各单元之间不存在互联且相互独立。设n、m分别为输入层v、隐藏层h的节点数，vi、hj代表可视层、隐藏层的第i、j个节点状态，则RBM某一给定状态（v，h）的能量函数表达式为：

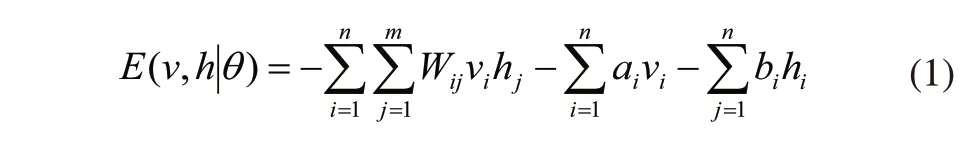
式中Wij是节点vi、hj之间的链接权重，ai，bj是可视层、隐藏层对应节点i，j的偏置，θ={Wij，ai，bj}是RBM模型参数。根据上述能量函数公式，可定义一个隐藏层和可视层的联合概率分布：

式中，Z为归一化因子，其表达式为：

若可视层与隐藏层被激活，令其状态值为1，则可视层与隐藏层的状态更新如下：

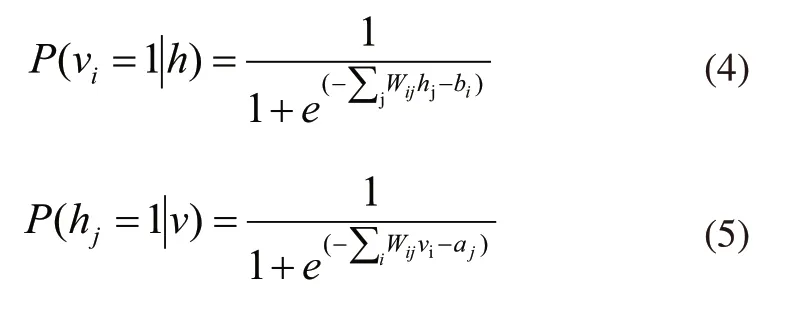
利用对比散度（Contrast Divergence，CD）的学习方法来训练RBM，可使重构误差收敛最快[9,10]。参数的更新规则如下：

其中，训练样本总数为T，样本t∈{1，2，3，…，T}。

预训练为无监督训练，但其所得DBM模型参数尚不能满足要求，需进一步采用BP算法对参数进行反向优化，此即为反向微调有监督训练。该反向优化过程以无监督训练所得参数作为有监督训练的初始化参数，从DBN网络的最后一层出发，对整个深层网络进行反向微调，若学习率、训练步数等参数设置得当，模型参数最终将收敛在一个恰当的数值[11]。

经过预训练与微调后，深度信念网络的训练过程就全部完成了。

2 配电网可靠性影响因素及分析步骤

对配电网供电可靠性相关影响因素分析之后，本文选择四大类数据作为深度信念网络的输入特征矢量：1）配电网拓扑结构；2）配电网线路参数（线路型号，线路长度等）；3）配电网元件可靠性参数（母线、线路、变压器、断路器、分段开关的故障率及平均故障修复时间等）；4）负荷类参数（负荷点及用户数等）。将配电网的四个主要可靠性指标：系统平均停电持续时间指标（System average interruption duration index，SAIDI）、系统平均停电频率指标（System average interruption frequency index，SAIFI）、用户平均停电累计时间（Average cumulative outage time，CAIDI）和平均用电可用率指标（Average service availability index，ASAI）作为深度信念网络的输出特征矢量（矢量元素个数Q=4）。

用于配电网可靠性分析的深度信念网络构建及训练过程如下：

1）确定DBN网络的结构。设置网络层数和各层节点个数，经反复优化调试，最后取隐含层数目为4层；每层节点数最大值为；其中p为配电网样本的网架结构个数，q为单个样本所含数据量。输出层神经元个数Q=4。

2）输入配电网可靠性分析的所有样本数据，所输入数据量为p×q，构建训练样本矩阵和测试样本矩阵。

3）对DBN网络模型参数进行优化。输入训练样本，逐步训练DBN中全部RBM，初步得到DBN网络参数值，之后将训练得到的参数利用BP算法进行反向优化训练，反复优化使重构误差μ降到3%以内，从而获得所需DBN网络模型。

配电网可靠性分析的DBN网络训练流程图如图2所示。

图2 配电网可靠性分析的DBN训练流程图

3 分析案例

3.1 基于DBN的配电网可靠性分析案例

配电网可靠性分析的问题本质上属于回归问题，使用DBN模型对此类问题进行很好的预测及分析。本文使用了包括手拉手、环网、多分段单联络、4乘6接线、放射状等各种类型在内的上万个配电网网架样本，对DBN网络进行训练。重构误差随迭代次数增加而变化的曲线，如图3所示：随着迭代次数的增加，重构误差逐步下降，当重构次数达到180次以后，网络重构误差稳定在3%以内，可见网络收敛速度相对较快，通过反复比较不同参数的DBN网络产生的误差，最终得到较优的DBN网络参数为[312，524，524，524，524，4]。将测试数据输入DBN网络，得到基于DBN的SAIFI、CAIDI、SAIDI和ASAI指标的部分测试集结果如图4所示，横坐标为100个测试集样本点，纵轴为对应的指标。从图中可以看出DBN的分析结果与真实值很接近，效果良好。

图3 DBN网络重构误差图

图4 基于SAIFI、CAIDI、SAIDI和ASAI指标的DBN结果图

3.2 与BP神经网络、Monte Carlo法的比较

配电网可靠性分析中的蒙特卡洛（Monte Carlo）法是传统方法中公认的比较精确的方法，BP神经网络是浅层神经网络的代表方法。本文将配电网可靠性指标SAIFI、CAIDI、SAIDI和ASAI作为评价指标，针对同一样本，将DBN这一深层神经网络的结果与Monte Carlo法、BP神经网络法进行比较。

选用均方根误差（Root Mean Square Error，RMSE）作为模型的评价指标，RMSE表示的是分析值与真实值偏差的平方与样本比值的平方根，可以较好的反映误差的实际情况。如式(10)所示。

其中，Wf为每一个样本点的分析值，Wt为每一个样本点的真实值。N为数据样本总数。对所选取的测试集的100个样本点用式(10)进行计算，得到的基于Monte Carlo、BP神经网络、DBN的RMSE值如表1所示。与Monte Carlo、BP神经网络两种方法相比较，对于SAIFI、CAIDI、SAIDI和ASAI指标，基于DBN的配电网可靠性分析的RMSE值是最小的，说明了DBN这一深度神经网络应用于配电网分析具有明显的优势。

表1 基于Monte Carlo、BP、DBN的RMSE值

在整个仿真实验过程中，Monte Carlo法的仿真计算时间和抽样样本数量有密切关系，为了得到足够精确的配电网可靠性，需要增加抽样次数，在确保最大精度的情况下，Monte Carlo模型所用时长为201s左右。对于神经网络，由于在训练过程中需要对训练数据进行反复迭代以及参数的反向更新，所以训练时间比测试时间要长，BP神经网络的训练时间在106.339s左右，测试所用时长为10.968s左右，DBN的训练时间108min左右，测试时间为11.441s左右。多次实验中，模型结构、训练策略皆未改变，选取的训练集、测试集规模也都相同，故几次实验的运算量也基本相同。显然，训练好后的DBN模型相比于蒙特卡洛法和BP神经网络法在精度和计算时间上有相对的优势。

4 结语

DBN模型是一种概率分布模型，具有强大的特征自动提取能力，能够充分挖掘数据中复杂的结构规律，被广泛应用于回归类问题的解决。

本文利用DBN模型的优点，提出了一种基于DBN模型的配电网可靠性分析方法。所用DBN模型由受限玻尔兹曼机（RBM）堆叠而成。在对所有RBM进行预训练后，采用BP算法进行反向微调，完成整个网络的训练过程。

训练完成后，采用DBN对配电网ASAI、SAIDI、CAIDI和SAIFI四大可靠性指标进行分析，并将分析结果与BP神经网络方法、蒙特卡洛模拟法的分析结果进行比较，结果显示，本文所提基于DBN方法的分析结果更为准确，且所用时间较短，一定程度上说明了深度学习方法在配电网可靠性分析的应用领域具有很大发展潜力。