基于L系统的三维分形树仿真

蒋杏丽，张岩

（沈阳师范大学数学与系统科学学院，辽宁沈阳，110034）

0 引言

分形，通常被定义为“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都是整体缩小后的形状”，即具有自相似的性质[1,2]。分形技术通常用来在计算机上模拟出自然界中具有非规则生长特性的植物。分形几何的概念 是美籍法国数学家曼德布罗[3]首先提出的，最初分形图的计算机绘制也只是停留在二维平面，后来，一个分形体爱好者丹尼尔·怀特提出一个大胆的方法，创造出令人称奇的3D分形影像[4]，并将它们命名为芒德球。本文在Matlab平台上利用L系统算法实现了三维虚拟场景的树木仿真，有效的展示了树木的生长和拓扑结构。

1 L系统算法

1.1 L系统的原理

L系统是由生物学家Aristid Lindenmayer[5]于1968年引进的一种字符串迭代重写机制[6]，是分形理论的一个重要分支，被认为是植物生长的数学理论。一个L系统可以用一个三元组（V，w，p）[7]来表示，其中V表示字母表；w是V中的一个非空字符串，代表初始形状；p是一个有限集合，代表重写规则。L系统的核心是字符串重写[8,9,10]，即使用一个重写规则或产生式的集合，对一开始定义好的初始字符串进行有限次数的迭代，再用龟形几何解释得到的新图形去改写替换原始的字符串[11]，最后获取分形图形完成三维仿真。

1.2 龟形解释

由于L系统的产生式、初始元以及重写后得到的元素都是以字符串的形式存在，所以为了让这些字符串能够具体的表示出某种图形，将其与植物模拟联系起来，我们引入了龟形这个概念。

龟形的当前状态由一个三元组(x,y,a)[12,13]来定义，其中笛卡儿坐标(x,y)表示海龟的位置，角度a为海龟的前进方向，可以解释为海龟面对的方向。给出步长d和角度的增量sita，海龟根据不同符号所代表的命令做出反应。

上面讲述的龟形解释是二维的，它可方便地扩展到三维空间，要对字符串进行三维龟图解释，关键是用三个向量H,L和U来表示空间龟的当前方位[14,15,16]。H、L、U分别为龟头的指向、左方、上方，这些向量具有单位长度且方向正交，即满足方程H X L=U。龟的旋转可表示为方程: (H,L,U) =(H,L,U) R[17],其中R是3X3的旋转矩阵。以下分别是绕矢量U、L和H旋转α的旋转矩阵R[18]:

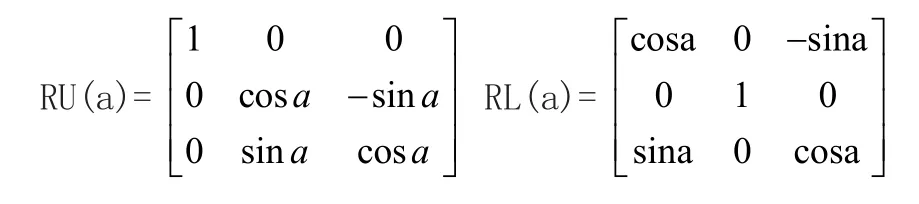
龟形位置初始化为笛卡尔坐标系统的原点,头矢量H指向y轴的正方向,左矢量L指向x轴负方向,向上的矢量U指向z轴的正方向。龟形根据参数的解释决定前进的方向和状态变化,如果有多个参数,第一个参数值决定龟的状态。本文中L系统用到的主要图形符号、其几何意义及具体实现代码如下表1。

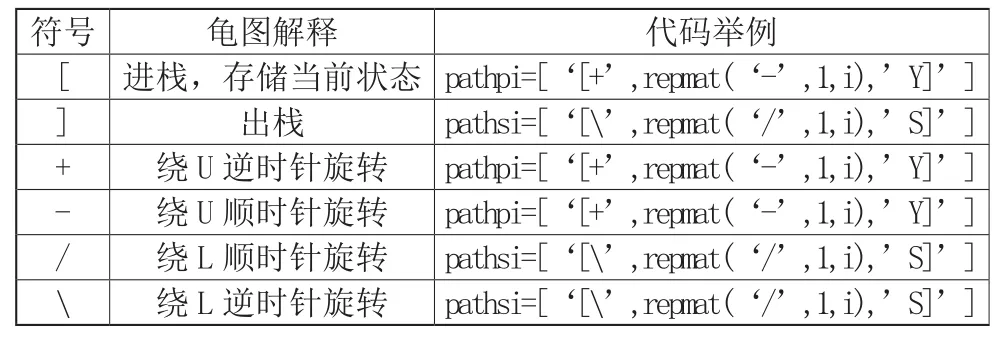
表1 图形符号解释

2 三维分形树的可视化

本研究利用Matlab进行模拟仿真。在模拟仿真三维生成树的时候，会产生大量的数据，造成存储和计算的能力[19]。MATLAB提供面向大数据处理的性能，可以方便、高效地格式化无法进入内存的文件数据，从而获得实际意义的实时处理效率[20]。

首先定义好树的初始字符串和产生式规则，设置树的生长深度来控制树的规模。再利用重写函数repmat()根据定义好的重写规则对字符串进行迭代重写，最后使用strrep()函数进行生长树替换，将初始字符串替换成重写之后的字符串。

实现代码：

nV=15; %纵向会有nV个节点的分支

nH=8; %横向会有nH个节点的分支

SET=’X’; %初始字符串

np=10; %主干上分枝数量

pathp=’’; %主干上空字符串

for i=1:np

pathpi=[‘[+’,repmat(‘-’,1,i),’Y]’]; % 字符串重写

pathp=[pathp,pathpi]; %连接每次重写后的字符串

end

pT=[‘T’,pathp,’X’]; %根据重写规则X对T中起始元是pathp字符串进行重写

ns=5; %主枝上分支数量

paths=’’; %主枝上空字符串

for i=1:ns

pathsi=[‘[’,repmat(‘/’,1,i),’S]’]; % 字符串重写

paths=[paths,pathsi]; %连接每次重写后的字符串

end

pS=[‘P’,paths,’Y’]; %根据重写规则Y对P中起始元是paths字符串进行重写

for k=2:nV;

SET=strrep(SET,’X’,pT); %生长树替换，纵向替换成pT字符串

end

for k=2:nH;

SET=strrep(SET,’Y’,pS); %生长树替换，横向替换成pS字符串

end

生长树替换完成后建立三维坐标以便在三维虚拟空间呈现出分形树的结构。首先求得生长控制参数诸如树干长度、树干延伸次数、树干收缩系数、树枝相对偏移角度以便在后续龟形图的实现中直接使用。其次设置龟形起点，初始方向，旋转角度，利用龟形解释依次去读取字符串的每个字符并解释为几何语言绘制出对应的图形。

运行程序后，在二维分形树图形界面上点击三维旋转按钮，拖动图形即可出现三维分形树图像，如图1和图2所示。

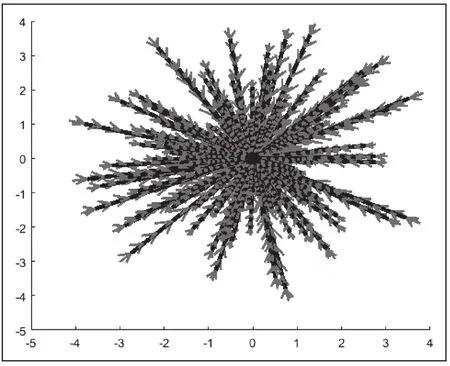
图1 二维分形树

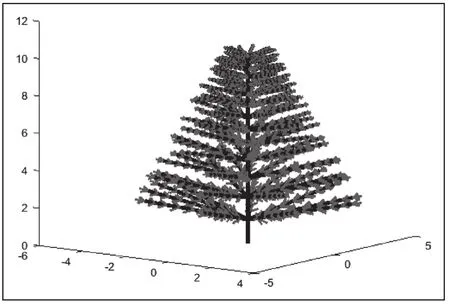
图2 三维立体分形树

3 结论

本文在已有的二维分形树研究的基础上进行了空间维度的扩展，在Matlab平台上利用L系统对树木结构进行解析，再根据定义的重写规则对树木初始字符串不断的迭代重写，完成树木的分形，最后使用龟形解释对分形得到的字符串用几何语言描绘成图像，实现了在三维空间的树木建模。但该模型仍然存在不足之处，今后可以有一个改进点，即更加生动形象的模拟出树枝摇曳的情形。