基于逻辑混合Petri网的混合系统建模与分析

刘 伟，史晓浩，孙红伟，2

(1.山东科技大学 计算机科学与工程学院，山东 青岛 266590；2.潍坊科技学院 智能制造学院，山东 寿光 262700)

Petri网是分布式系统的建模和分析工具，特别便于描述系统中进程或部件的顺序、并发、冲突和同步关系[1-2]，在许多实际系统的建模和分析中都得到了成功应用。随着Petri网理论和仿真技术的不断发展和完善，提出扩展的Petri网，如逻辑Petri网[3-4]、颜色Petri网[5]和混合Petri网[6]等。

逻辑Petri网是由Du等[7]定义的一种增广Petri网模型，它具有较简单的网络结构[8]，能够更好地描述实时协同工作系统模型的网结构，模拟和分析系统中的批处理功能与传值不确定性[9]。在逻辑Petri网中，变迁的输入和输出分别受到逻辑输入表达式fI和逻辑输出表达式fO的限制，这种受逻辑表达式约束的变迁称为逻辑变迁。逻辑变迁通过逻辑表达式表示输入/输出库所值的不确定性。显然，逻辑Petri网增强了Petri网的表达能力，更适合于复杂的建模需求。为了对实际系统进行建模和分析，提出多种扩展逻辑Petri网。为解决token处理中的系统优先级问题，文献[10]提出扩展逻辑Petri网。针对资源公平共享系统的调度问题,文献[11]提出队列逻辑Petri网。为分析B2C电子商务的信用风险问题,文献[12]提出基于博弈论和逻辑Petri网理论的信用风险博弈机制。

现有的逻辑Petri网模型以及扩展逻辑Petri网模型仅能建模离散系统，无法表征离散事件和连续动态之间的业务逻辑，难以应用于由相互作用的离散事件和连续行为组成的混合系统。而有效描述和分析离散事件和连续动态之间的相互作用是混合系统建模的关键，逻辑Petri网的特性使其能够充分挖掘活动之间的业务逻辑。因此，对逻辑Petri网进行扩展，将逻辑Petri网的逻辑表达能力应用到单变量混合系统中，提出一种新的混合系统建模方法具有重要的理论和现实意义。

基于上述问题，对逻辑Petri网进行扩展，并结合混合Petri网的思想，提出逻辑混合Petri网的概念。

1 基础定义

本节简要介绍逻辑混合Petri网建立过程中用到的基础知识，包括Petri网[13-14]、逻辑Petri网[15]和混合Petri网[16]，其中N是自然数集，N={0，1，…}，N+=N/{0}。R是实数集，R+是正实数集，R0=R++{0}。

定义1 (Petri网)Petri网PN= (P,T;F,M)是一个四元组,P和T是没有交集的非空有限集合，其中P是库所集，T是变迁集。F⊆ (P×T) ∪ (T×P)是有向弧的有限集合。M是标识函数。

定义2 (逻辑Petri网)逻辑Petri网LPN= (P,T;F,I,O,M)是一个六元组,P和T是没有交集的非空有限集合，其中P是库所集，T=TCD∪TI∪TO是变迁集。T包含且仅包含三个互斥的子集：TCD普通变迁集，TI逻辑输入变迁集以及TO逻辑输出变迁集。F⊆ (P×T) ∪ (T×P)是有向弧的有限集合。I(t)是从逻辑输入变迁到逻辑输入表达式的映射，O(t)是从逻辑输出变迁到逻辑输出表达式的映射。M是标识函数。

定义3 (混合Petri网)混合Petri网HPN = (P,T;Pre,Post,M,S)是一个六元组，P=Pd∪Pc是离散库所和连续库所的有限集合且Pd∩Pc=∅。T=TD∪TC是离散变迁和连续变迁的有限集合且TD∩TC=∅。Pre:P×T→R+是输入关联矩阵，Post:T×P→R+是输出关联矩阵。M:P→R是标识函数，M0表示初始标识。S是与连续变迁相关联的持续引发速度和引发时间的集合。对于t∈TC,S(t) = (vt,ht)，其中vt，ht∈R，vt，ht分别是与连续变迁t相关联的持续引发速度和引发时间。

2 逻辑混合Petri网

定义4 (逻辑混合Petri网)LHPN= (P,T;F,S,Usp,M,I,O,LC)称为逻辑混合Petri网，当且仅当

1)P=Pd∪Pc是库所的有限集合。

2)T=TD∪TC是变迁的有限集合,TD=TCD∪TI∪TO，TC=TCC∪TLC，其中

a)TD是离散变迁的集合。其中

i)TCD是普通离散变迁集合，其引发与输出均不受逻辑表达式的限制；

ii)TI是逻辑输入变迁集合，∀t∈TI，变迁t的引发受到逻辑输入表达式fI(t)的限制；

iii)TO是逻辑输出变迁集合，∀t∈TO，变迁t引发后的结果受到逻辑输出表达式fO(t)的限制。

b)TC是连续变迁的集合。其中

i)TCC是普通连续变迁的集合，其引发与输出均不受逻辑表达式的限制；

ii)TLC是逻辑连续变迁的集合。∀t∈TLC，变迁t的引发受到逻辑连续表达式fLC(t)的限制。

3)F=FT∪FC是有向弧的集合，FT∩FC=∅，其中

a)FT是普通有向弧的集合，其定义与定义1中F相同；

b)FC是控制弧的集合。控制弧只控制变迁的引发,变迁t∈T的引发不引起FC上库所的变化。

4)S=ST∪SP，ST∩SP=∅，其中

a) 对于t∈TC，ST(t) = (vt，ht)为与连续变迁相关的持续引发速度向量和引发时间的集合；

b) 对于p∈Pc，SP(p) = (vp，hp)为与连续库所相关的持续引发速度向量和引发时间的集合。

注意vt，ht，vp，hp∈R0。

5)USP是SP的计算函数。

6)M是标识函数，ℜ是标识数量函数。ℜ(p)表示库所p中token的数量。ℜ(Pd)∈N，ℜ(Pc)∈R0。

a)对于∀p∈Pd，库所p的标识M(p) = ℜ(p)；

b)对于∀p∈Pc，库所p的标识M(p)由ℜ(p)和SP组成。

7)I是逻辑限制输入函数，对∀t∈TI，I(t) =fI(t)。

8)O是逻辑限制输出函数，对∀t∈TO，O(t) =fO(t)。

9)LC是逻辑连续限制输入函数，对∀t∈TLC，LC(t) =fLC(t)。

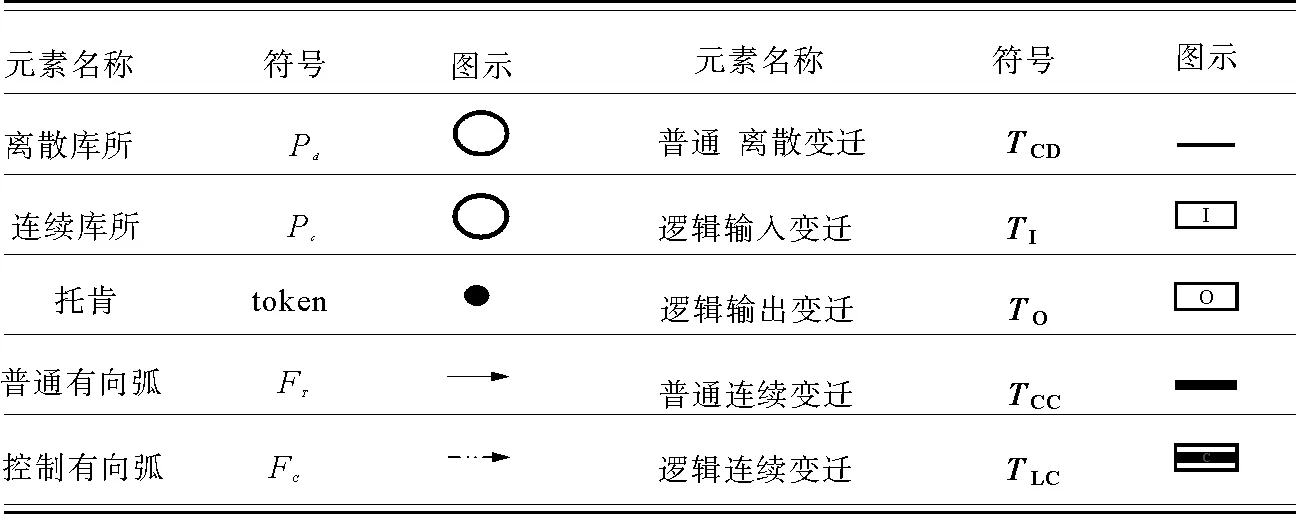
表1 逻辑混合Petri网的图示Tab. 1 Graphic presentation of logic hybrid Petri nets

定义5 (逻辑表达式f)令f为LHPN的逻辑表达式。p|M代表p在M下的逻辑值，·1·和·0·分别表示逻辑真值和逻辑假值。

对于∀p∈Pd，

(1)

对于∀p∈Pc，

(2)

f中的运算符由“∨”(逻辑或)，“∧”(逻辑与)和“¬”(逻辑非)组成。f=p1∨p2代表p1|M=·1·或p2|M=·1·。f=p1∧p2代表p1|M=·1·且p2|M= ·1·。¬·1·=·0·，¬·0·=·1·。将逻辑表达式中所有库所的逻辑值代入，得到的f|M=·1·/·0·为f在标识M下的逻辑值。

示例1如图1(a)所示，(p1,t1), (t1,p4) ∈FT; (p2,t1), (p3,t1) ∈FC。t1∈TLC，fLC(t1)=(p1∨p2)∧p3。只有满足逻辑表达式fLC时，才能引发变迁t1。fLC(t1)为真当且仅当p1∨p2，p3均为真。即p1|M=·1·或p2|M=·1·且p3|M=·1·。

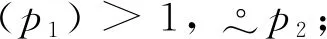
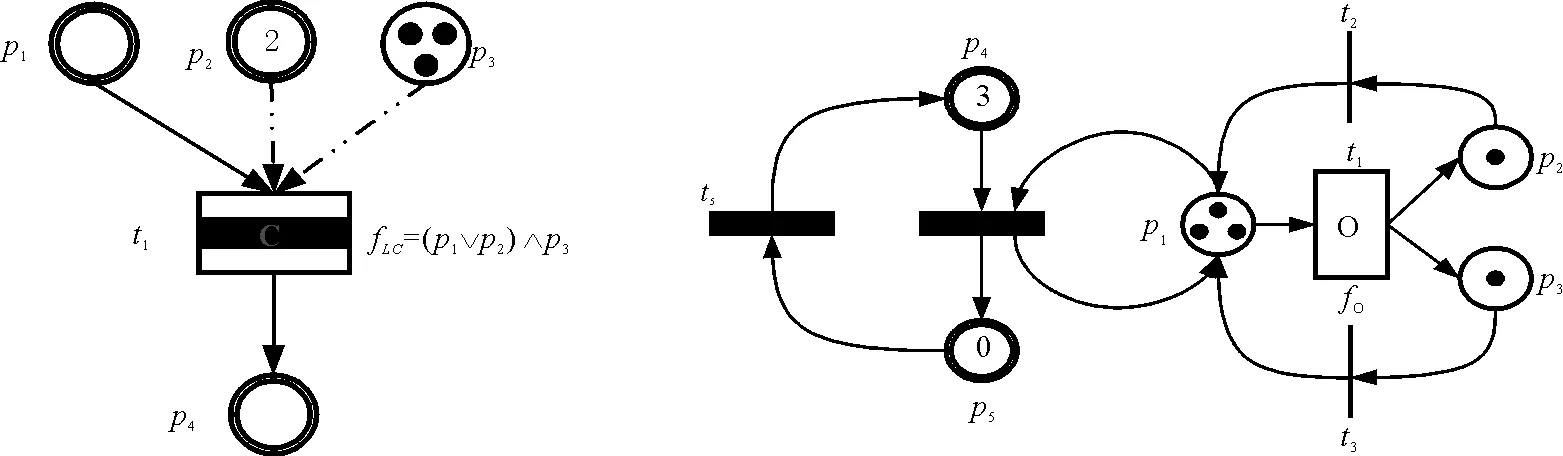
图1 两个简单的LHPN示例Fig. 1 Two simple LHPNs examples

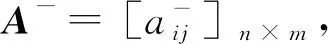
算法1Pre,Post,A-和A+的计算

输入：LHPN=(P,T;F,S,Usp,M,I,O,LC)

输出：Pre,Post,A-,A+

Step 0: 初始化：n=num[p],m=num[t],i∈{1, 2, …,n},j∈{1, 2, …,m},Pre←∅,Post←∅,A-←∅,A+←∅;

Step 1: For tj∈T, Do

Step 1.1: If (pi,tj) ∈FTThen

preij← 1;Pre⇐preij;

Step 1.1.1: Iftj∈TI∪TLCThen

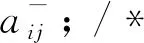
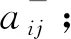
Step 1.1.2: Iftj∉TI∪TLCThen

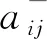
Step 1.2: If (pi,tj) ∈FCThen

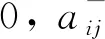
Step 1.3: If (tj,pi) ∈FTThen

postij← 1;Post⇐postij;

Step 1.3.1: Iftj∈TOThen

IffR= ∅ Then

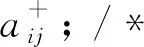
Else IffR≠ ∅ Then

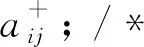
Step 1.3.2: Iftj∉TOThen

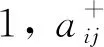
Step 2: 返回Pre,Post,A-,A+。

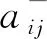
输入：fI(tj) fLC(tj),pi|M

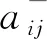
Step 1: If (pi,tj) ∈FTThen

Ifpi与任意p∈·tj/{pi}都不∃“∨” Then

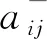
Else Ifpi与pk∈·tj/{pi}∃“∨” Then

Ifpi|M= ·1· Then

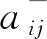
Else Ifpi|M= ·0· Then

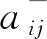
算法2的算法时间复杂度为O(1)。

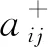
输入：fO(tj)fR(tj)

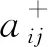
Step 1: If (tj,pi) ∈FTThen

IffR= ∅Then

Ifpi与任意p∈tj·/{pi}都不∃“∨” Then

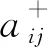
Else Ifpi与pk∈tj·/{pi}∃ “∨” Then

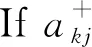
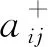
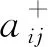
Else IffR≠ ∅ Then

If 关于pi的判定条件为真 Then

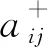
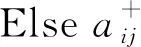
示例3对于图1(b)中的LHPN，如果O(t1) =fO(t1) =p2∨p3,则根据算法1，2，3，可以得到:

T1T2T3T4T5T1T2T3T4T5

T1T2T3T4T5T1T2T3T4T5

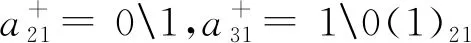
修正后的关联矩阵

W=Post*A+-Pre*A-。

(3)

代入示例3的数据，可得

T1T2T3T4T5

令σ为可达标识M0执行的引发序列。对于∀tj∈TD，σj为变迁tj在序列σ中的引发次数。对于∀tj∈TC，σj为变迁tj在序列σ中的vt和ht。如果引发序列σ满足M0[σ>Ms，则可以得出基本方程：

ℜs= ℜ0+Wσ。

(4)

取σ= (1, 1, 1, 2; 2, 1, 1)，可以得到：

如果O(t1) =fO(t1) =p2∧p3，则相应的结果为[4 1 1 0 3)]T。

定理1如果∃t∈TO，fO中∃“∨”且fR= ∅，M0[σ>Ms，则ℜs具有不确定性。

证明1:基于算法1，2，3，如果∃t∈TO，fO中∃“∨”且fR= ∅，则Step 1因为无fR限定变迁输出，因此fOΘA+≫不确定的A+；Step 2 因为Post，Pre，A-都为确定值，A+不确定，因此W=Post*A+-Pre*A-ΘW≫不确定的W；Step 3M0[σ>Ms。因为ℜ0，σ为确定值，W不确定，因此ℜs= ℜ0+WσΘℜs≫不确定的ℜs，ℜs具有不确定性。定理1得证。

定理2如果∃t∈TO，fO中∃“∨”且fR≠ ∅或者fO中不∃“∨”，M0[σ>Ms，则ℜs是确定值。

证明2:如果∃t∈TO，fO中∃“∨”且fR≠ ∅或者fO中不∃“∨”，则Step 1 如果fO中∃“∨”且fR≠ ∅，因为fR限定变迁输出，因此fRΘA+≫确定的A+；如果fO中不∃“∨”，fOΘA+≫确定的A+；Step 2: 因为Post，Pre，A-和A+都为确定值，因此W=Post*A+-Pre*A-ΘW≫确定的W；Step 3M0[σ>Ms。因为ℜ0，W，σ都为确定值，因此ℜs= ℜ0+WσΘℜs≫确定的ℜs，ℜs是确定值。定理2得证。

定理3如果∀t∉TO，M0[σ>Ms，则ℜs是确定值。

证明3:如果∀t∉TO，则Step 1 根据算法1，2，3得出Post，Pre，A-和A+都为确定值；Step 2 因为Post，Pre，A-和A+都为确定值，因此W=Post*A+-Pre*A-ΘW≫确定的W；Step 3:M0[σ>Ms。因为ℜ0，W，σ都为确定值，因此ℜs= ℜ0+WσΘℜs≫确定的ℜs，ℜs是确定值。

定义8函数USP是连续库所Sp的计算函数。在tj∈TC开始引发与引发结束时，函数USP对∀pi∈ (·tj∪tj·) ∩Pc的SP中vpi和hpi进行计算和更新。SP中vpi和hpi求解算法如算法4所示。

算法4SP中vpi和hpi的计算

输入：LHPN= (P,T;F,S,Usp,M,I,O,LC),tj∈T

输出：vpi,hpi

Step 0 初始化：vpi← (0, 0, …, 0),hpi← 0, [P,T] ← ∅, [T,P] ← ∅,TM(n),TM(i,j),TM(j,i);

Step 1 While (tj∈TC开始引发) Do

更新当前时间TM(n);

Step 1.1 For ∀pi∈·tj∩PcDo

TM(i,j) ←TM(n),vpi←vpi-vtj; [P,T] ⇐ (pi,tj);/*将(pi,tj)写入[P,T]*/

Step 1.2 Ifhpi> 0 Then

Else Ifhpi= 0 Thenhpi←htj;

Step 1.3 For ∀pi∈tj·∩PcDo

TM(j,i) ←TM(n),vpi←vpi+vtj; [T,P] ⇐ (tj,pi);

Step 1.4 If (hpi> 0) Then

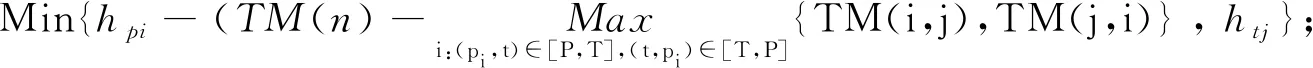
Else Ifhpi= 0 Thenhpi←htj;

Step 2 While (tj∈TC引发结束) Do

更新当前时间TM(n)；

Step 2.1 For ∀pi∈·tj∩PcDo

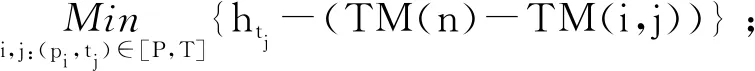
Step 2.2 For ∀pi∈tj·∩Pc, Do

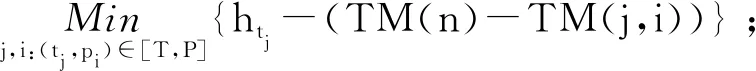
Step 3 返回vpi,hpi。

算法4的算法时间复杂度为O(|pi|)。

定理4如果多个tj∈TC∩ (·pi∪pi·)同时开始引发且vpi=0，hpi= 0。则pi的vpi和hpi的计算公式为：

(5)

(6)

注意，tf∈·pi∩TCI，tl∈pi·∩TCI，其中TCI表示被引发的连续变迁集合。

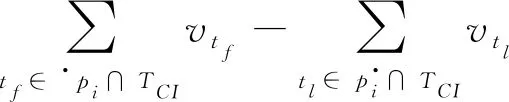
定义9 (变迁引发规则)

1)对于∀t∈TCD，如果∀p∈·t∩Pd，ℜ(p) ≥pre(p,t)且∀p∈·t∩Pc，ℜ(p) > 0，则t在M下使能。

2)对于∀t∈TI，I(t)=fI(t)。如果逻辑输入表达式fI(t)在标识M下的逻辑值为真，则t在M下使能。

3)对于∀t∈TO，O(t)=fO(t)。如果∀p∈·t∩Pd，ℜ(p)≥pre(p,t)且∀p∈·t∩Pc，ℜ(p)>0，则t在M下使能。对于t·，fO(t)|M′=·1·。

对于∀t∈TD，如果t使能，则它可以引发，在标识M下引发生成一个新的标识M′。ℜ′(p)的计算公式为：

∀p∈·t, ℜ′(p) = ℜ(p) -a-(p,t) *pre(p,t)；

(7)

∀p∈t·, ℜ′(p) = ℜ(p) +a+(p,t)*post(p,t)。

(8)

4) 对于∀t∈TCC，如果∀p∈·t∩Pd，ℜ(p) ≥pre(p,t)且∀p∈·t∩Pc，ℜ(p) > 0，则t在M下使能；如果t使能，则它可以引发。

5) 对于∀t∈TLC，LC(t) =fLC(t)。如果逻辑连续表达式fLC(t)在标识M下的逻辑值为真，则t在M下使能；如果t使能，则它可以引发。

对于∀t∈TC，假设引发开始时刻为tms，引发结束时刻为tme，tme=tms+ht。在任意时刻tm∈ [tms,tme]，标识变为M′。ℜ′(p)的计算公式为：

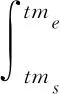
(9)

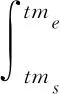
(10)

∀p∈·t∩Pd, ℜ′(p) = ℜ(p) -a-(p,t)*pre(p,t);

(11)

∀p∈t·∩Pd, ℜ′(p) = ℜ(p) +a+(p,t) *post(p,t)。

(12)

注意，当t∈TC引发开始和结束时,根据定义8与算法4，函数USp对∀p∈ (·t∪t·) ∩Pc的vpi和hpi进行计算和更新。上述考虑的输入弧都为普通有向弧，控制弧连接的库所标识不会随变迁的引发而改变。

3 实例分析

3.1 微电网系统的LHPN模型

微电网包括分布式发电机、储能系统和公用电网上的负荷等，其提出可将再生能源有效地整合到电力和能源系统中，为用户提供高质量和高可靠性的电力。以文献[16]中微电网系统为例，建立如图2所示LHPN模型。

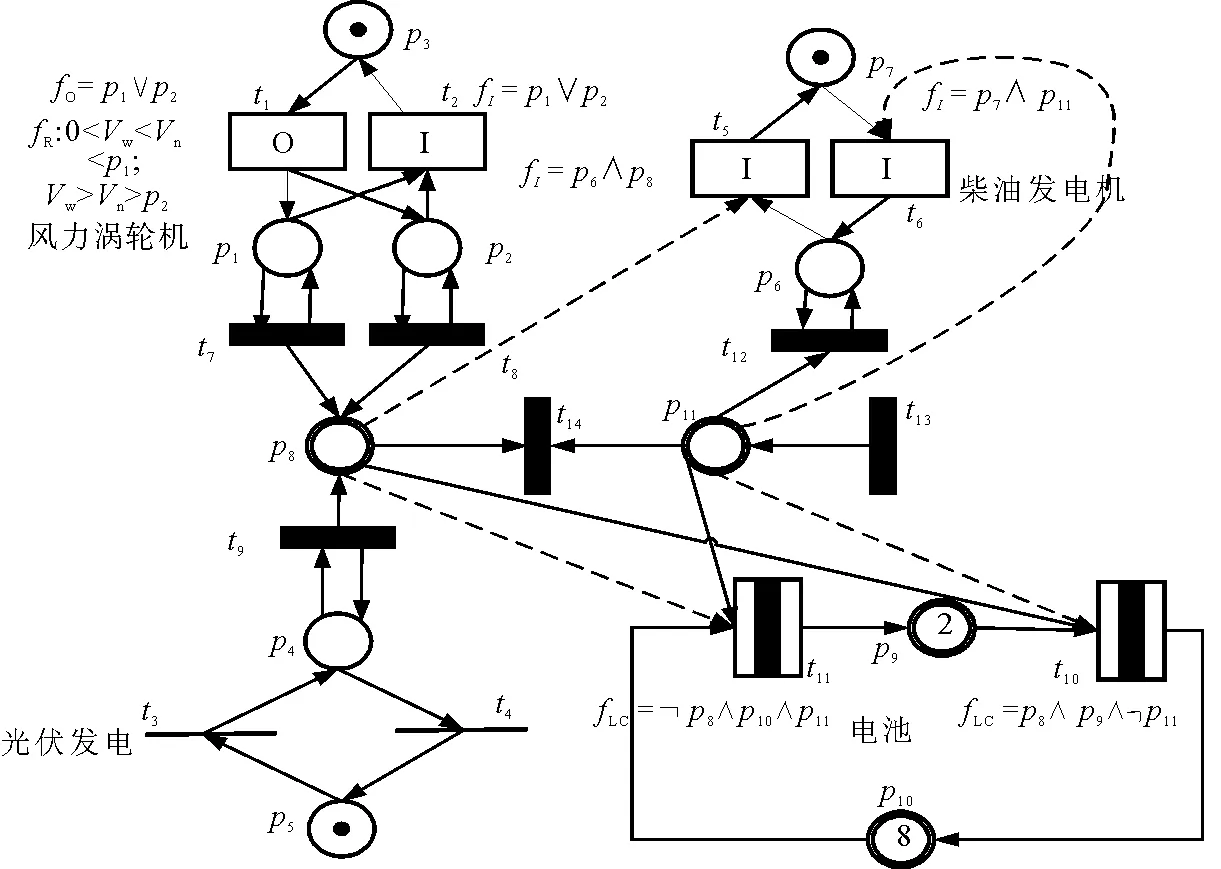
图2 微电网的LHPN模型Fig. 2 LHPN model of microgrid

3.2 系统业务逻辑挖掘

与LPN相比，LHPN中的逻辑表达式定义进行了扩展，能够有效地描述和分析离散变量和连续演化过程之间的相互作用，充分挖掘混合系统中的业务逻辑。例如f(t11) = ¬p8∧p10∧p11，经过逻辑推理可得：¬p8∧p10∧p11→t11，p8∨ ¬p10∨ ¬p11→ ¬t11。即变迁p11的引发受到库所p8，p10，p11的限制，只有p8= ·0·，p10= ·1·，p11= ·1·时，变迁t11才能引发。这意味着在该微电网系统中，只有当微电网系统中风力发电与光伏发电产生电量为0，且电池存储电量和负载需求大于0时，变迁t11才能引发。电池进入放电状态，满足用户负载需求。而当p8，p10，p11状态发生改变，使得fLC= ·0·时，则变迁t11结束引发，即电池结束放电状态。而同时也可以推出，t11→ ¬p8∧p10∧p11，¬t11→p8∨ ¬p10∨ ¬p11。扩展之后的逻辑表达式能够很好地运用到混合系统建模分析中，并能够对混合系统中的业务逻辑进行充分挖掘。

基于逻辑表达式的微电网业务逻辑挖掘：¬p8∧p10∧p11→t11，p8∨ ¬p10∨ ¬p11→ ¬t11，t11→ ¬p8∧p10∧p11，¬t11→p8∨ ¬p10∨ ¬p11，p8∧p9∧ ¬p11→t10，¬p8∨ ¬p9∨p11→ ¬t10，t10→p8∧p9∧ ¬p11，¬t10→ ¬p8∨ ¬p9∨p11，p6∧p8→t5，¬t5→ ¬p6∨ ¬p8，p7∧p11→t6，¬t6→ ¬p7∨ ¬p11。

3.3 修正表达

3.4 系统可达图

基于文献[16]中微电网系统的相关数据，根据定义9变迁引发规则，以及算法4连续库所SP的算法，得到系统运行的可达图，如图3所示。

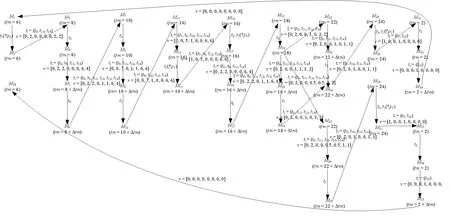
图3 系统标识可达图Fig. 3 System marking reachability

其中，各个可达标识的信息如下：

M1= [0,0,1,0,1,0,1,0(0;0),2(0;0),8(0;0),0(2;2)]，

M2= [0,1,0,0,1,0,1,0(0;0),2(0;0),8(0;0),0(0;0)]，

M3= [0,1,0,0,1,0,1,0(0;0),2(0;0),8(0;0),0(6;2)]，

M4= [0,1,0,1,0,0,1,0(0;2),2(0;0),8(0;0),0(2;2)]，

M5= [0,1,0,1,0,0,1,0(0;0),2(0;0),8(0;0),ε(2;2)]，

M6= [0,1,0,1,0,1,0,0(0;0),2(1;2),8(-1;2),ε(0;0)]，

M7= [0,1,0,1,0,1,0,0(0;0),4(0;0),6(0;0),ε(6;4)]，

M8= [0,0,1,1,0,1,0,ε(1;4),4(1;4),6(-1;4),ε(0;0)]，

M9= [0,0,1,1,0,1,0,ε(1;4),4(1;4),6(-1;4),0(0;0)]，

M10= [0,0,1,1,0,1,0,ε(0;0),4(-1;4),6(1;4),0(0;0)]，

M11= [0,0,1,1,0,0,1,ε(0;0),0(-1;2),10(1;2),0(6;2)]，

M12= [1,0,0,1,0,0,1,ε(0;0),0(-1;2),10(1;2),0(0;0)]，

M13= [1,0,0,1,0,0,1,0(0;0),0(0;0),10(0;0),0(0;0)]，

M14= [1,0,0,1,0,0,1,0(0;0),0(0;0),10(0;0),0(6;2)]，

M15= [0,1,0,1,0,0,1,0(0;2),0(0;0),10(0;0),0(2;0)]，

M16= [0,1,0,1,0,0,1,0(0;2),0(0;0),10(0;0),ε(2;0)]，

M17= [0,1,0,1,0,1,0,0(0;2),0(1;2),10(-1;2),ε(0;2)]，

M18= [0,1,0,1,0,1,0,0(0;4),2(1;4),8(-1;4),ε(3;4)]，

M19= [0,1,0,0,1,1,0,0(0;0),2(1;4)/(0.5;4),8(-1;4)/(-0.5;4),ε(0;4)]，

M20= [0,1,0,0,1,1,0,ε(0;0),2(1;4),8(-1;4),0(0;0)]，

M21= [0,1,0,0,1,0,1,ε(0;0),2(1;4),8(-1;4),0(0;0)]，

M22= [0,1,0,0,1,1,0,0(1;2),6(1,4),4(-1;4),ε(1;2)]，

M23= [0,1,0,0,1,1,0,ε(1;2),6(0;0),4(0;0),0(0;2)]，

M24= [0,1,0,0,1,0,1,ε(1;2),6(-1;2),4(1;2),0(0;2)]，

M25= [0,1,0,0,1,1,0,0(1;2),4(0.5,4),6(-0.5;4),ε(0;0)]，

M26= [0,1,0,0,1,1,0,ε(1;2),4(0;0),6(0;0),0(0;0)]，

M27= [0,1,0,0,1,0,1,ε(0;0),4(0;0),6(0;0),0(0;0)]，

M28= [0,1,0,0,1,0,1,ε(0;0),4(-1;2),6(1;2),0]，

M29= [1,0,0,0, 11,0,ε(1;2),4(-1;2),6(1;2),0(0;2)]，

M30= [0,1,0,0,1,0,1,ε(0;0),2(-1;2),8(1;2),0(0;0)]，

M31= [1,0,0,0,1,0,1,ε(1;2),2(-1;2),8(1;2),0(0;0)]，

M32= [1,0,0,0,1,0,1,ε(1;2),2(-1;2),8(1;2),0(0;4)]，

M33= [0,0,1,0,1,0,1,ε,2(-1;2),8(1;2),0(0;2)]，

M34= [0,0,1,0,1,0,1,0(0;0),2(0;0),8(0;0),0(0;0)]，

M35= [1,0,0,0,1,0,1,ε(1;2),0(-1;2),10(1;2),0(0;0)]，

M36= [0,0,1,0,1,0,1,ε(0;0),0(-1;2),10(1;2),0(0;0)]，

M37= [0,0,1,0,1,0,1,0(0;0),0(0;0),10(0;0),0(0;0)]，

M38= [0,0,1,0,1,0,1,0(0;0),0(0;0),10(0;0),0(0;0)]。

生成的LHPN可达性图用于显示系统离散状态以及连续状态。此外，决策点上所有可能选择均被列出。通过对不同的决策方式下产生的状态标识进行分析比较，决策者可以选择最佳的操作方案。

LHPN模型在连续库所添加了SP，与文献[16]中HPN模型相比，系统状态得到更加准确的描述，所有连续动态的变化趋势均被量化且列出。对比文献中的HPN模型的系统可达图，根据LHPN模型得到的系统可达图能够更加详尽地描述系统各状态下连续库所对应行为的变化趋势。例如M19= [0,1,0,0,1,1,0,0(0;0),2(1;4)/(0.5;4),8(-1;4)/(-0.5;4),ε(0;4)]，由于M19→M22和M19→M25为两种不同的操作方案，不仅会生成不同的状态标识，且相应连续库所会产生不同的变化趋势，这些都在M19中得到准确描述。

3.5 标识求解方程

根据定义7的LHPN的标识求解方程，可以求取系统当前状态标识经过一定操作及连续运行之后的系统状态标识。当确定操作方案后，即确定了引发序列，可直接根据ℜs= ℜ0+Wσ，对系统的状态标识进行求解。虽然该方程无法对连续库所对应的SP进行求解，但能够快速求得系统标识中各部分的token数量。与根据变迁引发规则一步步求解的方法相比，能够有效提高运算效率。以定义7中例子可见，在计算之前根据算法1、2、3确定Pre、Post、A-和A+，并据此求出修正矩阵。状态标识求解时只需根据ℜs=ℜ0+Wσ直接得出。而根据变迁引发规则需要计算两次离散变迁和两次连续变迁引发结果，运算较为复杂。通过LHPN的标识求解方程可对求得的标识可达图进行验证，经计算验证，图3所示标识可达图为正确的。

4 结论

在扩展逻辑Petri网定义的基础上，提出逻辑混合Petri网概念用于建模和分析混合系统。扩展逻辑表达式的定义，提出一种确定连续库所逻辑值的方法，使LHPN可以应用到混合系统建模中。在逻辑输出中引入修正函数，解决了LPN输出的不确定性表达问题，并提出LHPN的标识求解方程。在连续库所上加入连续变化速度和时间，提出相应的求解算法，较HPN能够更加详尽地描述系统各状态下连续库所对应动态行为。LHPN能够对混合系统的离散事件和单变量连续行为进行准确描述和分析，并能对离散事件与连续行为之间的业务逻辑进行挖掘。以一个微电网系统为例，构建LHPN模型，对系统业务逻辑进行挖掘分析，验证了模型的可行性和有效性。通过系统可达图计算验证了方法的可靠性。实例证明该模型能够有效地对微电网系统进行建模和分析。将此建模方法用于混合系统的最优控制和决策有待进一步研究。此外，此建模方法仅适用于单变量连续系统，而对于多变量连续系统需要进一步研究。