高职院校数学教育专业《空间解析几何》教学改革策略

马桂州

摘要：文章分析了当前高职院校数学教育专业的《空间解析几何》课程在教学中存在的一些问题：课程理论性强，学生学习兴趣缺乏;课时总量少，课程内容多;教学方式不合理;教师授课忽视学生个体差异。针对存在的这些问题，文章探讨了要如何进行教学改革，提出了一些策略：穿插数学史及数学故事激发学生学习兴趣;根据学生培养定位，优化教学内容;兼顾传统教学手段，合理使用多媒体技术;重视学生的个体差异，实施分层教育。

关键词：高职院校 数学教育 空间解析几何 教学改革

Teaching Reform Strategy of Space Analytic Geometry for Mathematics Education Major in Higher Vocational Colleges

MA Guizhou

（Shanwei Polytechnic， Shanwei， Guangdong Province， 516600 China）<！-- 依次为单位，市，省，邮政编码中国（ShangqiuPolytechnic， Shangqiu， He'nanProvince， 476000China） -->

Abstract： This paper analyzes some problems existing in the teaching of Space Analytic Geometry course of mathematics education major in higher vocational colleges： The course is highly theoretical and students lack interest in learning; The total number of class hours is less and the content of courses is more; The teaching method is unreasonable; Teachers ignore students' individual differences in teaching. In view of these problems， this paper discusses how to carry out teaching reform and puts forward some strategies：Interspersed with mathematical history and mathematical stories to stimulate students' interest in learning; According to the orientation of how to cultivate students， optimize the teaching content; Give consideration to the traditional teaching methods and use the multimedia technology reasonably; Pay attention to students' individual differences and carry out stratified education.

Key Words： Higher vocational colleges; Mathematics education; Space Analytic Geometry; Education reform

《空间解析几何》是高职院校数学教育专业的一门专业基础课程，通过本课程的学习，可以培养学生的空间想象能力和运用代数方法解决几何问题的能力。作为一门重要的基础课程，《数学分析》《数学建模》等课程的学习都离不开《空间解析几何》的知识以及研究方法。因此，研究《空间解析几何》的教学模式和教学改革是非常必要的。笔者结合自己多年的教学经验，对高职院校数学教育专业的《空间解析几何》课程在教学中存在的一些問题以及如何进行教学改革提出一些看法。

1 《空间解析几何》课程教学中存在的问题

1.1课程理论性强，学生学习兴趣缺乏

《空间解析几何》是一门基础理论课程，课程理论性较强，课程内容相对枯燥。这门课程一般开设在大学一年级的第一学期，教师授课时面对的是刚进入大学的新生。大学一年级+的新生刚刚度过了三年紧张的高中学习生涯，对于他们来说，大学的新生活是相对轻松的。很多学生把主要精力投在学生社团、学生会的各种活动中，而在学习上则投入比较少，这种现象在高职院校表现得更为明显。高职院校的学生，在学习自觉性上是比较差的，当他们遇到理论性较强的《空间解析几何》课程时，自然而然就缺乏兴趣了。

1.2课时总量少，课程内容多

近几年在教育部深化教学改革精神的指导下，实践性课程在高职院校的重要性越来越凸显。在这种背景下，高职院校存在大量缩减理论课程学时的现象，因此在高职院校中，理论课程学时普遍不够。以笔者所在学院为例，该学院数学教育专业《空间解析几何》目前的开设学时数为72学时，这72学时除去因期末复习、节假日停课等各种特殊情况占用的学时之后，实际上只有60多节的课程讲授学时。而该学院数学教育专业《空间解析几何》选用的教材是吕林根、许子道编的《解析几何》，这个版本的教材是比较经典的，教材的内容也是比较详尽的，要在这60多节的课程讲授学时内完成这么多内容的教学是不现实的。

1.3教学方式不合理

解析几何以前的传统授课方式是黑板课，教师在黑板上板书授课。黑板板书授课在讲解定理的推导过程或者计算题的演算过程时有一定的优势。但是缺点也很明显，一方面是板书慢，课容量小;另一方面是在展示空间图形时不够直观，不能够很好地让学生观察到几何形体的特征。

随着多媒体技术的发展，教师在课堂中使用多媒体课件的现象逐渐普遍化。多媒体课件的使用，能够直观生动地展现空间几何图形，学生因此能够更直观地去观察和认知几何形体的特征。

但是在使用多媒体技术时，有一些教师走入了误区：有的教师过度追求课件的华丽，将更多的心思用在制作界面的视觉效果上，而不是放在课件展现的教学内容的锤炼上，课堂效果因而不理想;还有的教师在授课时忽视了其他教学手段的辅助，完全依靠课件的使用，由于缺乏多种教学手段的相互配合而减弱了课堂效果;更为常见的是，有一些教师没有结合课堂上的实际情况，也没有考虑学生的认知水平，一股脑地采用多媒体课件满堂灌，导致课堂上的课容量过多，课件一页页翻得很快，学生因为课堂节奏过快而没法及时掌握到课堂的基本知识。

1.4教师授课忽视学生个体差异

高职院校的学生入学录取分数较低，学生们在各个科目上的基础参差不齐，有的学生是高考数学分数高，其他科目分数低，有的学生是高考其他科目分数高数学分数低，也有的学生是各科都差，学生之间存在比较大的个体差异。但是，在上课时，不少老师没有考虑到学生之间的个体差异，课堂上课时没有区别对待，这就容易使得数学基础相对薄弱的那部分学生因为听不懂而厌学，同时也满足不了数学基础较好的部分学生。这样一刀切的授课方式，久而久之，自然会导致课堂教学效果不理想。

2 《空间解析几何》教学改革策略

2.1穿插数学史及数学故事，激发学生学习兴趣

由于枯燥的理论比较容易让学生失去学习兴趣，所以《空间解析几何》的课堂教学要尽量避免一味讲理论，如果教师能够在课堂中适当穿插跟解析几何有关的历史或者故事，将有利于激发学生的学习兴趣^[1]。

例如，教师在上开学第一节课时，可以跟学生谈一谈解析几何的发展背景。14到16世纪时，欧洲兴起了文艺复兴运动，文艺复兴运动的兴起促进了科學和文化的发展，在这种背景下，天文、力学、航海等领域得到很大发展，原来的几何学不能适应科学技术发展的需求，因此推动了17世纪初解析几何的诞生。

教师在上课时，也可以跟学生谈一谈解析几何的创立者笛卡尔和费马的生平。笛卡尔是17世纪时法国的哲学家和数学家，笛卡尔年幼时很坎坷，一岁时母亲染病去世，自己受母亲感染从小就体弱多病。八岁读书时，学校为了照顾笛卡尔的身体，特许他早上不来学校上课，因此笛卡尔每天早上醒来后，就躺在家里的床上读书，这种经历使得笛卡尔自小就养成了喜欢安静、勤于思考的习惯。笛卡尔读大学期间对数学产生了浓厚的兴趣，并在之后的人生中深入研究，得到很多学术成果，这里面就包括了解析几何的学说。费马是和笛卡尔同个时代的法国数学家，他的主要职业是律师，数学仅仅是费马从事律师工作的业余爱好，但是他在数学上的成就却比很多全职的数学工作者都辉煌。费马独立于笛卡尔发现了解析几何的基本原理，因此数学史上认为解析几何这门学科是笛卡尔和费马共同创立的。费马在数学的其他分支都有很多不俗的研究成果，其中最出名的是提出费马大定理，这个定理的证明困惑了全世界数学家350多年，直到1995年才被英国数学家怀尔斯证明^[2]。

教师在给学生上“标架与坐标”这个章节时，可以跟学生讲讲笛卡尔建立坐标系的小故事：有一次，笛卡尔生病卧床休息，在床上躺着的时候，笛卡尔看到天花板边缘的墙角有一只蜘蛛，这只蜘蛛织了个大网，这引起了笛卡尔的注意。笛卡尔突然想到一个问题，能不能借助墙和墙之间、天花板和墙之间的三条交线对蜘蛛进行定位呢？受到这个问题的启发，笛卡尔研究并建立了坐标系的理论^[3]。

这些跟解析几何有关的历史或者小故事，能够吸引学生的注意力，活跃课堂气氛，让学生对解析几何产生浓厚的兴趣，促使学生自发地去进一步研究解析几何^[4]。

2.2根据学生培养定位，优化教学内容

由于在《空间解析几何》课程的教学中存在着课时总量少、课程内容多的困境，因此必须进行教学内容的优化以及整合。讲授《空间解析几何》课程的教师要根据人才培养方案对学生的培养定位，对教材的内容进行取舍。

在人才培养方案中，对于高职院校的学生，在理论方面的要求没有本科层次的学生高，而教材的最后两章是关于二次曲线和二次曲面的一般理论，这一部分内容属于比较深奥的理论知识，因此这两章的内容是可以考虑删去不讲的。教材第一章“向量与坐标”中有一部分向量的知识点是学生在中学阶段已经接触过的，教材的这些知识点是对中学相关知识的巩固和加深，因此，对于这些知识点，可以考虑适当略讲。教材第二章的主要内容是轨迹与方程，第三章的主要内容是平面与空间直线，第四章的主要内容是柱面、锥面、旋转曲面与二次曲线，这些知识点都是中学阶段接触比较少或者完全没有接触过的，同时也是这门课比较核心的知识，因此考虑详讲。附录“矩阵与行列式”这一部分的知识，是数学教育专业的另外一门基础学科《高等代数》的核心内容^[5]，在《高等代数》课程中会进行全面系统地授课，但是按照这两门课程上课时的教学进度安排，学生在《高等代数》课程中学到矩阵与行列式这一方面知识的时间比《空间解析几何》课程用到这方面知识的时间要晚，因此，在《空间解析几何》课程的教学中，教师可以考虑对附录“矩阵与行列式”进行整合，选择性地简单介绍一部分跟《空间解析几何》理论体系有关的知识点，其它的知识点留待教《高等代数》的教师去讲授。

2.3兼顾传统教学手段，合理使用多媒体技术

教师仅用传统教学手段上课或者过度使用多媒体技术上课都存在着一些问题。那么如何在课堂中兼顾传统的教学手段，合理使用多媒体技术？教师可以考虑将传统的教学手段和多媒体技术手段相结合，利用黑板板演进行课程的导入、定义的诠释、定理的推导和习题的计算，利用多媒体平台展示空间几何形体的形态、演示空间几何形体的动态生成过程。这样既能节省画几何形体占用的大量时间，增加课容量，又能充分展现空间解析几何中几何形体的直观性。

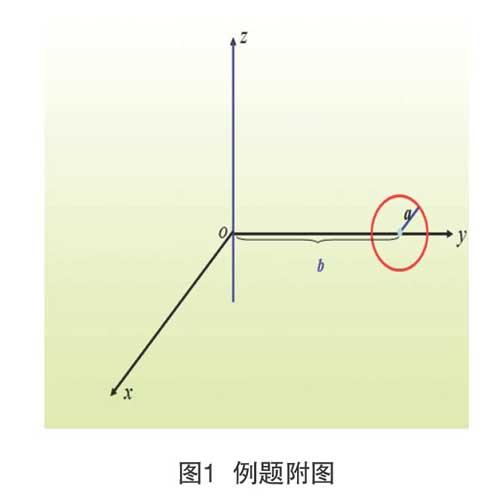
例如：将圆（图1）绕z轴旋转，求所得旋转曲面的方程^[6]。

教师先简单复习求旋转曲面方程的方法，然后利用黑板进行这道习题的演算，边演算边整理解题过程如下：

解：因为该圆绕z轴旋转，所以在方程中保留z不变，而y用代换，得到将该圆绕z轴旋转而成的旋转曲面方程为，

即，

或

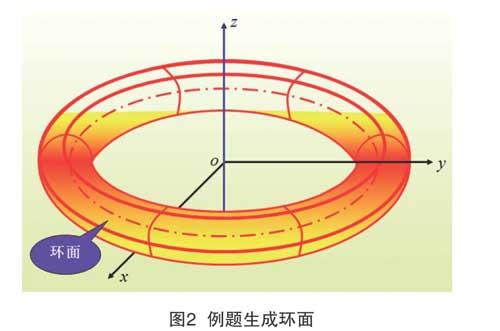
这个曲面我们称之为环面，游泳圈和自行车的内胎都是环面的形状。

教师利用多媒体平台展示该环面的动态生成过程，加深学生对环面的理解，生成后的环面如图2所示。

<！-- 为黑白刊物 -->

2.4重视学生的个体差异，实施分层教育

教师授课忽视学生之间的个体差异容易导致课堂教学效果不理想，为了规避这种情况，教师在课堂教学中可以考虑进行分层教育。

首先，可以将教学内容进行分层，将教学内容分成必学知识和选学知识。必学知识要求全体学生都要掌握，考核时必考;选学知识不要求所有学生掌握，考核时不考。比如，教师在讲“曲面的方程”这一節时，可以把“曲面的方程”、“曲面的参数方程”这两个基本的知识点定为必学知识，把“球坐标系”、“柱坐标系”这两个学生比较难理解并且对后续内容没影响的内容定为选学知识。

其次，教师也可以对学生进行分层，根据学生的学习基础，把学生分成若干层次，同时将练习题也分成若干层次，让各个层次的学生根据自己的学习能力选做对应层次的练习题。教师在对学生进行分层时，可以先进行摸底测试，根据测试得到的结果，把学生分为甲、乙两层，甲层对应优秀的学生，乙层对应普通的学生。从学生的心理健康角度考虑，对学生分层时不建议分多一个差生对应的丙层，给学生贴上丙层的标签对学生的心理健康是非常不利的。同时，把课堂习题和课后习题分为困难、中等、容易三层。甲层的学生必做中等和容易两个层次的习题，选做困难的习题;乙层的学生必做容易的习题，选做中等和困难的习题。

总之，高职院校数学教育专业的《空间解析几何》课程具有其特殊性，对学生的理论学习能力和空间想象能力都有一定的要求，因此决定了这门课程的教学改革是一个长期的工作，需要众多专业教师的不断摸索研究，教师们在教学中要根据学生的特点，努力设计好每一节课。

<！-- 含以下目录中的参考文献不少于2篇（为便于核查符合下面条件的参考文献的刊名或整条用红字标注）：不包含本刊①当代体育科技②科技资讯③文化创新比较研究④南京体育学院学报（自然科学版）⑤硕士、博士学位论文⑥影响因子为0.5及以上的期刊。（核查办法见各刊网站）⑦外文参考文献 --><！-- 参考文献需在文中按顺序上标 -->

参考文献：

[1]陈琳.数学史融入高中解析几何教学的研究[D].岳阳：湖南理工学院，2020.

[2]蔡天新.新费马大定理及其论证探索[J].数学进展，2020（5）：635-639.

[3]杨培奇.数学史融入高中数学教学的现状调查与改进策略[D].长沙：湖南师范大学，2020.

[4]佟小华.数学史融入高等数学教学的意义和方法[J].西部素质教育，2019（10）：192-213.

[5]盛兴平，唐剑，辛大伟，徐传友.高师院校数学专业三基课程关联性教学的研究与探讨[J].大学数学，2016，32（6）：106-116.

[6]吕林根，许子道.解析几何[M].北京：高等教育出版社，2019.