基于ANSYS Workbench的介质泄漏对密炼机转子端面密封影响的摩擦静力学分析
汪传生,张 健,张 萌,聂万富,温南南,边慧光
(青岛科技大学 机电工程学院,山东 青岛 266042)
密炼机是橡胶成型工艺过程中的必要设备,密炼机的混炼过程使得橡胶与各种配合剂达到良好的混合和分散效果[1]。相较于开炼机,密炼机在混炼全过程中都处于密封状态[2],混炼过程初始阶段密炼室内充满橡胶、粉体和液体小料混合物,这些混炼物料颗粒非常小,均可通过转子与密炼室间的环形间隙泄漏,因此在转子端面与密炼室间存在密封装置[3]。该装置由一个静密封环和一个动密封环组成,彼此可相互滑动,动密封环随转子旋转,静密封环固定在静环套中。为保证动静密封环的使用寿命,通常在动静密封环的接触面间注入润滑油以确保良好的密封效果[4-5],但仍不能保证密封完全,粒径极小混炼物料颗粒会在混炼过程中进入接触界面。
本工作通过ANSYS Workbench软件中的结构静力(Static Structure)分析模块,对密炼机转子端面无介质密封(混炼物料颗粒不进入端面)和介质密封(混炼物料颗粒进入端面)2种情况进行有限元分析,研究介质(混合物料)泄漏对动静密封环使用寿命的影响。
1 动静密封环有限元模型的建立
1.1 几何模型简化
密炼机转子端面密封结构如图1所示,处理前动静密封环结构如图2所示。
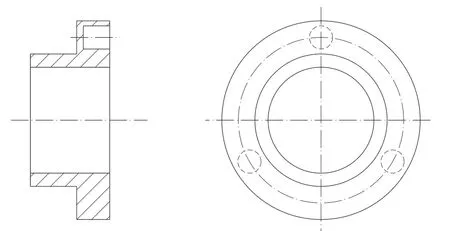
图2 处理前动静密封环结构Fig.2 Structure of dynamic and static sealing ring before treatment
图1所示的密封结构采用单端密封,静密封环固定端均布3个直径4 mm的小孔,用来安装压紧导柱。在有限元模拟中,孔的存在会产生应力集中,且使得网格划分复杂,由于3个孔仅用来安装压紧导柱,对接触瞬态分析影响不大,因此为了提高网格划分质量,减少计算量,动静密封环简化模型去掉了孔,如图3所示。
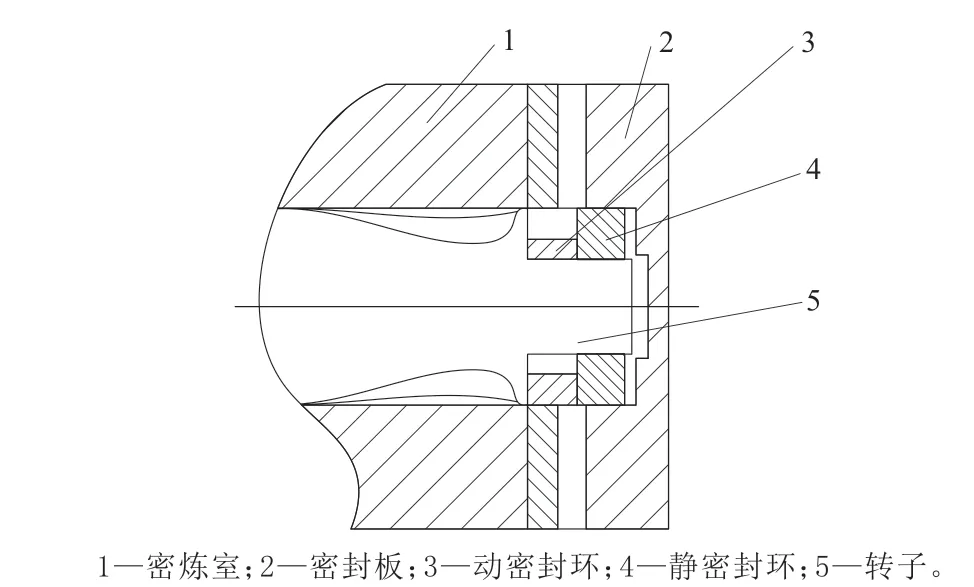
图1 密炼机转子端面密封结构Fig.1 Sealing structure of mixer rotor end face
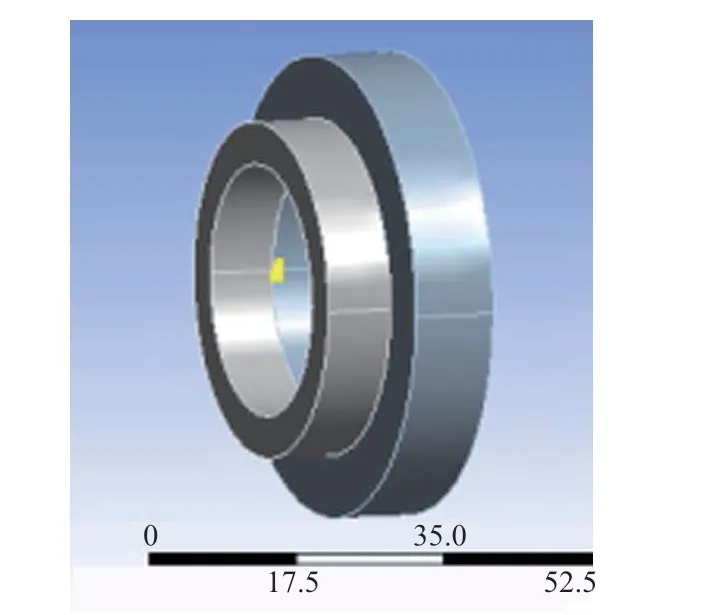
图3 动静密封环有限元模型Fig.3 Finite element model of dynamic and static sealing ring
1.2 材料参数设置
动静密封环皆为45#钢,弹性模量为196~206 GPa,泊松比为0.24~0.28。在实际工况中,为提高动密封环的耐磨性能和静密封环的摩擦性能,动密封环表面堆焊硬质合金,静密封环45#钢采取调质处理,因此设置动静密封环的弹性模量为200 GPa,密度为7.89 Mg·m-3,泊松比为0.28。自定义泄漏介质材料弹性模量为0.007 8 GPa,泊松比为0.33。
1.3 接触对参数设置及网络划分
1.3.1 接触模型
弹性力学中,接触问题是指2个物体在受压状态下所发生的力学行为,包括局部应力和应变等;在实际工程中2个物体相互接触并产生相对运动时接触表面即产生摩擦;在有限元中,以节点来定义接触,理论上2个节点在某一个区域或线上恰好重合即被认为发生了接触。但是在计算中不能精确描述节点的接触,需要设置接触区域。实际计算过程中,当某一个时间增量或载荷步中接触物体移动超出了接触距离,就会被认为发生了穿透[6-12]。
接触模型可描述为求区域内位移场,使系统势能在接触边界条件约束下达到最小,即
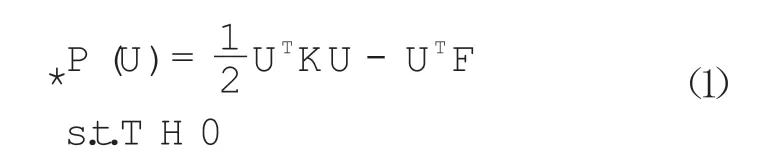
式中,K,U和F分别为有限元位移法中的刚度矩阵、未知结点位移向量和结点荷载向量。
实际计算中,由于相互接触的物体材料属性、力学性能等不同,有限元将接触划分为两类:刚性体-柔性体接触和柔性体-柔性体接触。在密炼机密封装置的动静密封环中,动密封环在密炼室内部,静密封环在密炼室端面,更换静密封环较为容易,动静密封环材料均为45#钢,但动密封环表面堆焊的硬质合金较硬,而静密封环调质处理的45#钢较软,所以采用的有限元模型为刚性体-柔性体接触模型。
1.3.2 接触公式
穿透在实际接触物体之间不会发生,因此在有限元分析软件中采用程序强制接触协调来控制穿透,以期模拟真实接触状态。罚函数法接触模型如图4所示,当接触协调性不被强制时就会发生穿透。Workbench Mechanical模块中提供了罚函数法[5]、拉格朗日乘子法[6]、增广拉格朗日乘子法[7]3种强制协调的接触公式。
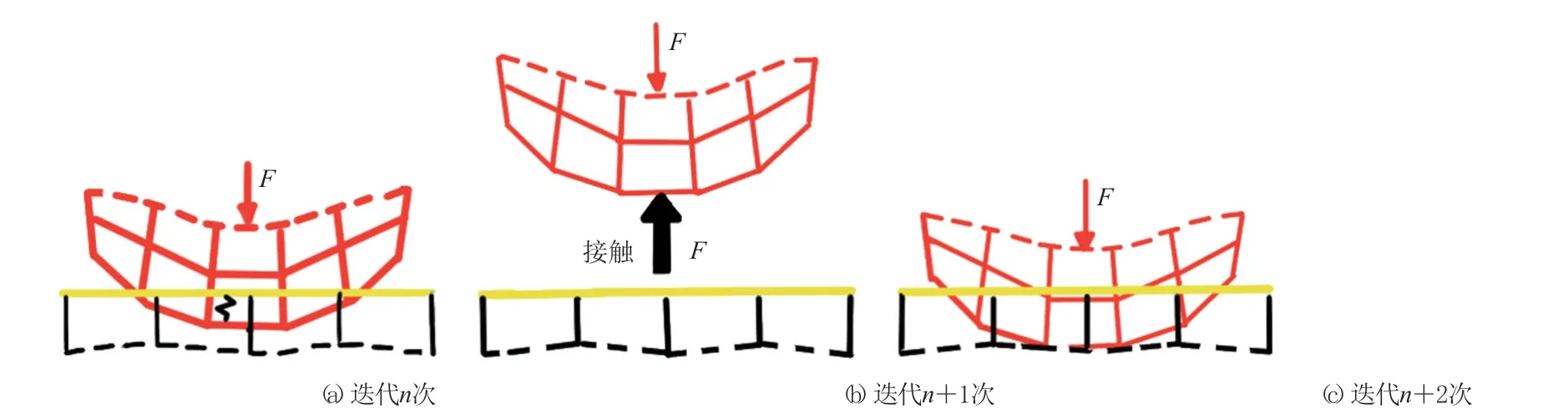
图4 罚函数法接触模型Fig.4 Contact model of penalty function method
(1)罚函数法。罚函数法要求有限的穿透量在交界面处产生接触压力,保持系统平衡需要此接触压力,即接触压力必须大于零。然而,实际的接触物体相互不穿透,因此为了得到最高精度,应使发生在接触界面处的穿透量最小,这意味着理想的接触刚度应非常大,但是刚度值太大会引起收敛困难。如果接触刚度太大,微小的穿透即会产生很大的接触压力,在下一次迭代中可能会将接触面推开,采用过大的接触刚度通常会导致收敛振荡且发散。
(2)拉格朗日乘子法。拉格朗日乘子法接触模型如图5所示,其实质是增加一个附加自由度(接触压力)来满足不可穿透条件。
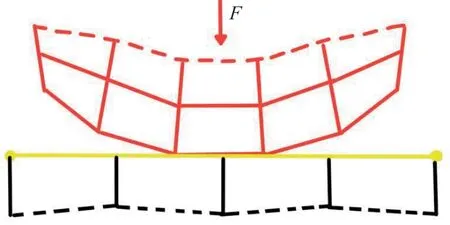
图5 拉格朗日乘子法接触模型Fig.5 Contact model of Lagrange multiplier method

(3)增广拉格朗日乘子法。将以上两种方法结合起来,就是增广拉格朗日乘子法,其接触模型如图6所示。接触协调性基于惩罚刚度确定,一旦达到平衡,检查穿透容差,如果有必要,接触压力增大,迭代继续。
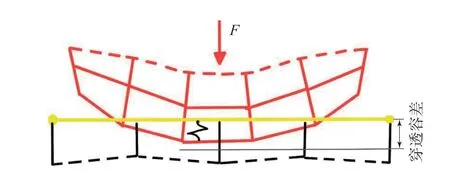
图6 增广拉格朗日乘子法接触模型Fig.6 Contact model of augmented Lagrange multiplier method
综上所述,在此次模拟中,静密封环表面设置为接触面,动密封环表面设置为目标表面,端面接触摩擦因数为0.2,端面介质摩擦因数为0.3,默认增广拉格朗日乘子法,使结果更容易收敛。模型采用正六面体划分网格,网格总数为44 800,网格划分模型如图7所示。

图7 动静密封环接触网格划分模型Fig.7 Meshing model for contact between dynamic and static sealing ring
1.4 边界条件设置
动密封环随着转子旋转,静密封环固定且受横向压力,两表面接触起到密封作用,因此在动密封环上施加转动惯性负荷,转动速度为120 r·s-1,横向压力为1 MPa,静密封环非接触端面施加固定约束,计算时间设置为1 s,将大变形“large deflection”设置成“on”。
1.3.3 接触摩擦因数
在密封端面摩擦磨损过程中,理论上金属材料的摩擦因数与表面接触面积及相对运动速度无关,但是在密炼机密封装置中摩擦因数随着介质环境发生变化,且介质环境影响较大,甚至改变端面接触应力和应变的大小。端面密封副的摩擦因数包括接触摩擦因数和介质摩擦因数。摩擦因数(f)的计算公式为
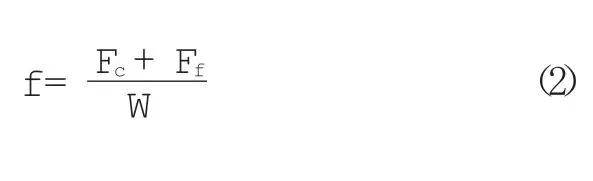
2 结果与讨论
2.1 动静密封环接触端面的应力分析
在动静密封环端面直接接触和介质接触2种状态下,对动静密封环接触端面进行应力分析,结果如图8所示。
从图8可以看出,在端面直接接触和介质接触时,在均匀密封压力作用下,动静密封环的受力均沿圆周方向均匀分布,在接触端面压力最大,摩擦力也最大,磨损较为剧烈。
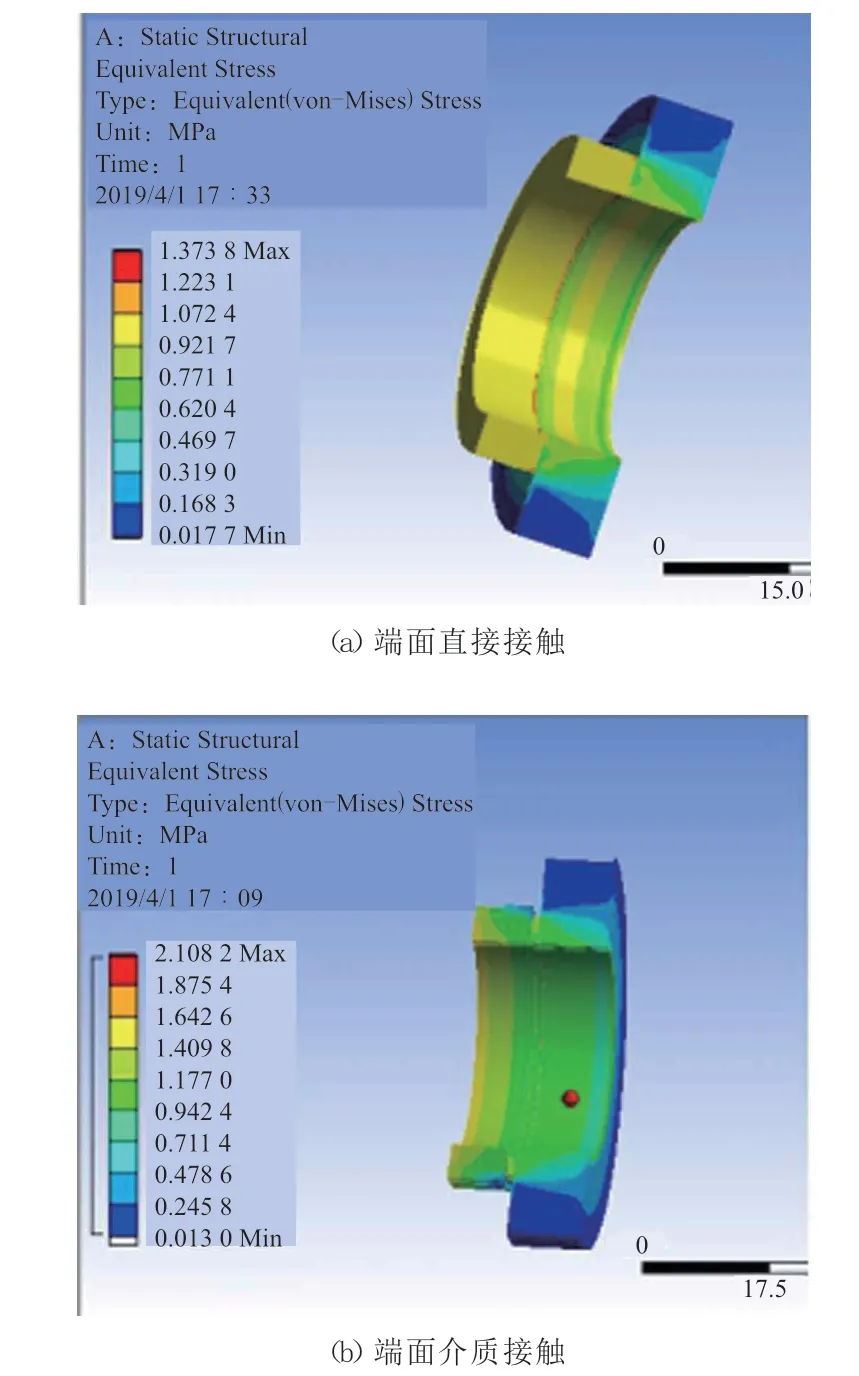
图8 不同接触状态下动静密封环接触端面的等效应力云图Fig.8 Equivalent stress nephograms of contact end face of dynamic and static sealing ring under different contact states
对比图8(a)与(b)可以看出,动静密封环端面直接接触时,其最大应力为1.373 8 MPa,端面介质接触时,其最大应力为2.108 2 MPa,相较于直接接触增大了53%。因此,密炼过程中,混合物料泄漏会导致动静密封环端面摩擦磨损加剧,动静密封环更易损坏甚至失效。
2.2 动静密封环接触端面的应变分析
在动静密封环端面直接接触和介质接触2种状态下,对动静密封环接触端面进行应变分析,结果如图9所示。
从图9可以看出,在端面直接接触和介质接触时,在均匀密封压力作用下,动静密封环接触端面的应变均不是很大,这是因为密封压力较小,结构钢材本身的刚度足够抵抗应变的变化。
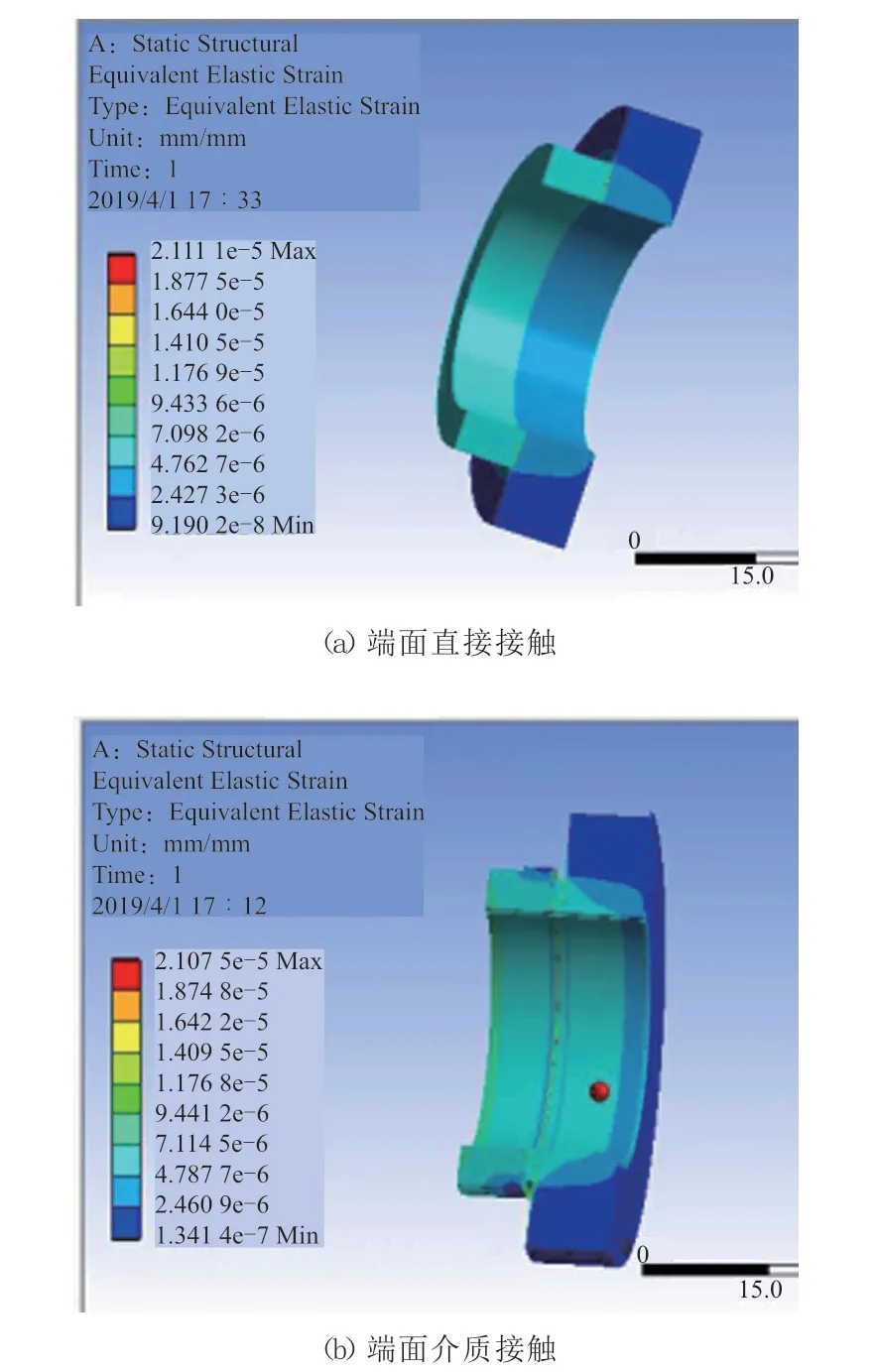
图9 不同接触状态下动静密封环接触端面的等效应变云图Fig.9 Equivalent strain nephograms of contact end face of dynamic and static sealing ring under different contact states
对比图9(a)与(b)可以看出,动静密封环直接接触时,其最大应变为2.111 1×10-5mm,端面介质接触时,其最大应变为2.107 5×10-5mm,两种状态下基本保持一致。
在动静密封环端面直接接触和介质接触2种状态下,静密封环端面的等效应变云图见图10。
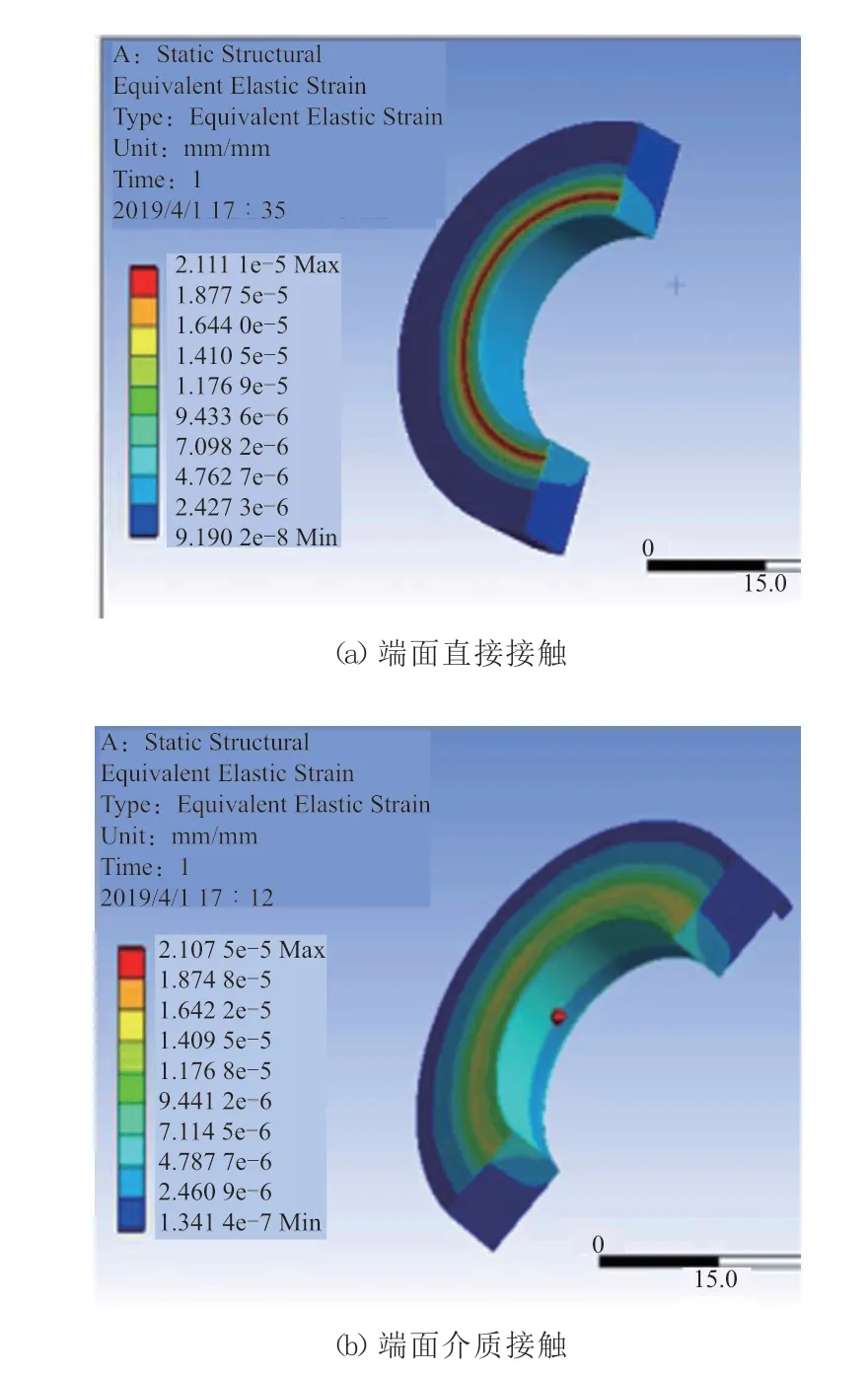
图10 不同接触状态下静密封环端面的等效应变云图Fig.10 Equivalent strain nephograms of end face of static sealing ring under different contact states
从图10可以看出,与在端面直接接触时相比,在端面介质接触时静密封环的应变小且更加均匀,这是因为应变发生在中间不均匀的介质中,对端面的总应变影响较小。
3 结语
利用ANSYS Workbench软件中结构静力分析模块,对密炼机转子端面与密炼室室壁间的密封装置——动静密封环进行有限元分析,得到如下结论。
(1)动静密封环制造所采用的45#钢的刚度足够,其端面直接接触和介质接触所产生应变基本一致,混炼物料介质的泄漏不会使动静密封环产生很大变形。
(2)动静密封环接触端面压力最大,导致端面摩擦力最大,磨损最剧烈。
(3)混炼物料的泄漏使动静密封环端面接触由直接接触变为介质接触,端面处应力增大53%,端面摩擦磨损更剧烈,易导致动静密封环损坏甚至失效。

