基于ABAQUS 的两种应力强度因子计算方法对比

姜 旭，寇园园，石朝龙

（1.西安石油大学石油工程学院，陕西西安 710065；2.西安石油大学陕西省油气井及储层渗流与岩石力学重点实验室，陕西西安 710065）

断裂力学[1]在钻井工程领域中运用甚广，其研究日趋复杂化、多样化，由于工程实践的复杂性，大量的解析解和经验公式充斥在实践的各个环节[2]。表征裂纹尖端应力场强度的“应力强度因子（SIF）”是井壁裂纹分析的核心内容[3]。裂纹尖端应力场的奇异性明显，很大程度上造成了其求解误差，解析解和经验公式都给工程时间带来了巨大的偏差与困扰[4]。因而，建立高效、高精度的计算方法至关重要。在ABAQUS 中内置有SIF的求解方法，本文将通过算例对ABAQUS 内置求解方法与传统“外推法”进行对比，得出若干结论。

1 基于单元应力的外推法计算SIF 的理论基础

基于应力的外推法是计算应力强度因子最直接的方法，由应力强度因子的极限定义式（1）便知，KI是对应于裂尖（r=0）时的极限值，但是直接计算无法使得r=0。为了得到KI，便可使用合理外推的方式来计算KI，方法如下：

在运用ABAQUS 中易直接查询（Inquery）到裂尖前端单元积分点上的应力值σy和对应的积分点的坐标值r，且其可以被输出（Output）。同样可以在绘图软件中画出σy和r 的关系，不难得到应力分布曲线（见图1）。这时，当单元被细化，其应力值将趋向于无穷，文献中大都称其为应力奇异。

图1 裂纹尖端的应力分布示意图

为了得到KI值，用ri来表示应力积分点与裂尖之间的距离，与其相对应的KIi共同组成数据对（ri，KIi）。在得到数据对之后，运用最小二乘法来拟合。

此时，令：

设KI=Ar+B，当r=0 时，KI≈KI（r=0）=B，显然，易得每个数据点的偏差为KIi-KIi。

根据最小二乘法，拟合出的最优结果满足：

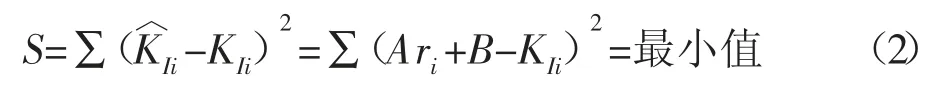
对A 和B 求偏导得到线性方程组，再进一步用ri和KIi相关的因子来表示A（斜率）和B（截距）的表达式如下：

因此，只要做出反映σy和r 的关系曲线，则其截距为应力强度因子。

2 ABAQUS 中两种SIF 计算方法的实现[5-8]

2.1 ABAQUS 内置方法计算SIF

ABAQUS 中建立半宽W=100 mm，半高H=200 mm，厚度1 mm 的平板模型（见图2），该平板中心预制有一条裂纹，其半裂纹长度为20 mm；建立弹性模量为2×105MPa，泊松比为0.25 的“弹性各向异性”固体材料；经过装配、网格划分、指定裂纹和裂纹扩展方向以及裂纹尖端场的奇异性设置等操作。进行边界条件设置和应力加载。（施加均布拉力30 MPa，下端两角固定）提交作业后，裂纹尖端应力（见图3）。

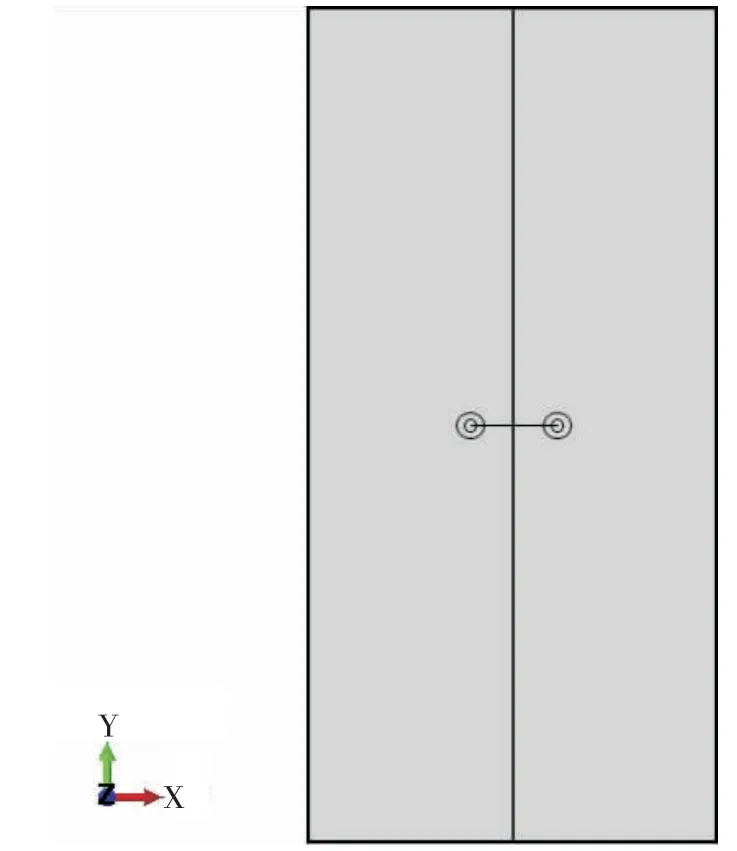
图2 裂纹平板模型

图3 Job 提交后的裂纹尖端沿Y 方向的正应力分布

在后处理中输出的Data 文件中，ABAQUS 内置方法计算出的SIF 值（见图4）。

图4 Data 文件中输出的SIF 计算结果

2.2 ABAQUS 中外推法的实现过程

在后处理中，运用“单元应力的外推法”，通过定义“path”输出（20，0）处至（25，0）处对应的应力值，输出rpt 文件。将该文件中的数据导入表格中进行处理（见表1）。

表1 基于rpt 文件的数据处理

表1 基于rpt 文件的数据处理（续表）

基于表1 中数据绘制KI的变化趋势图（见图5）。其截距238.26 即为KI值，该值与ABAQUS 求解器所求平均值244.13 的相对误差仅为2.46%。

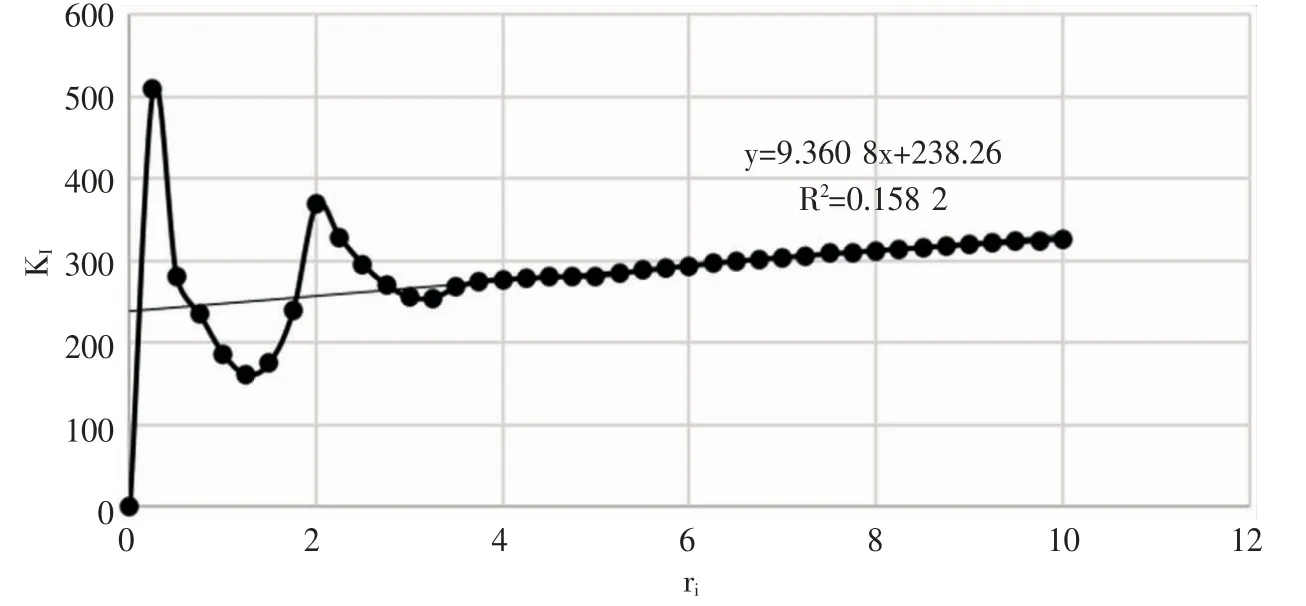
图5 KI 随ri 变化的趋势图

略去表1 中前21 组数据，排除裂尖的奇异性干扰。可求得更加接近的KI值：243.36（见图6），其与ABAQUS 求解器所求平均值244.13 的相对误差缩至0.32%，相关性系数从0.158 2 上升至0.989 2。

图6 KI 随ri 变化的趋势图

3 ABAQUS 求解器求解与外推法的求解值的对比

基于以上计算过程，进行对比（见表2）。

表2 SIF 求解结果对比

4 结论

（1）ABAQUS 求出的值与应力外推法的求解值相近，说明了ABAQUS 内置的算法已经相当精确。

（2）在削弱裂尖部位的奇异性影响后，可使得其与ABAQUS 内置算法逼近，说明ABAQUS 的计算精度是可靠的。数据的剔除过程随意性较大，客观上造成计算结果的不确定性。

（3）基于应力的两次外推过程，其差异化结果印证了裂纹尖端场所具有的奇异性特点，去掉裂纹尖端附近的点可有力减弱奇异性对应力强度因子的影响。

（4）裂纹尖端应力强度因子的研究对象是“裂纹尖端”，而实际计算中却因尖端数据不收敛而舍弃了该部分数据，这造成了逻辑上的悖论。